4.1: Funções exponenciais
- Page ID
- 189219
- Avalie funções exponenciais.
- Encontre a equação de uma função exponencial.
- Use fórmulas de juros compostos.
- Avalie funções exponenciais com base\(e\).
A Índia é o segundo país mais populoso do mundo, com uma população de cerca de\(1.25\) bilhões de pessoas em 2013. A população está crescendo a uma taxa de aproximadamente a\(.2\%\) cada ano. Se essa taxa continuar, a população da Índia excederá a população da China até o ano de 2031. Quando as populações crescem rapidamente, costumamos dizer que o crescimento é “exponencial”, o que significa que algo está crescendo muito rapidamente. Para um matemático, no entanto, o termo crescimento exponencial tem um significado muito específico. Nesta seção, examinaremos as funções exponenciais, que modelam esse tipo de crescimento rápido.
Ao explorar o crescimento linear, observamos uma taxa de variação constante — um número constante pelo qual a produção aumentou para cada aumento unitário na entrada. Por exemplo, na equação\(f(x)=3x+4\), a inclinação nos diz que a saída aumenta\(3\) cada vez que a entrada aumenta\(1\). O cenário no exemplo da população da Índia é diferente porque temos uma variação percentual por unidade de tempo (em vez de uma mudança constante) no número de pessoas.
Definindo uma função exponencial
Um estudo descobriu que a porcentagem da população vegana nos Estados Unidos dobrou de 2009 a 2011. Em 2011,\(2.5\%\) a população era vegana, aderindo a uma dieta que não inclui nenhum produto de origem animal — sem carne, aves, peixes, laticínios ou ovos. Se essa taxa continuar, os veganos\(10\%\) constituirão a população dos EUA em 2015,\(40\%\) em 2019 e\(80\%\) em 2050.
O que exatamente significa crescer exponencialmente? O que a palavra duplo tem em comum com o aumento percentual? As pessoas usam essas palavras de forma errante. Essas palavras são usadas corretamente? As palavras certamente aparecem com frequência na mídia.
- A variação percentual se refere a uma alteração com base em uma porcentagem do valor original.
- O crescimento exponencial se refere a um aumento baseado em uma taxa de variação multiplicativa constante em incrementos iguais de tempo, ou seja, um aumento percentual da quantidade original ao longo do tempo.
- O decaimento exponencial se refere a uma diminuição baseada em uma taxa de variação multiplicativa constante em incrementos iguais de tempo, ou seja, uma diminuição percentual da quantidade original ao longo do tempo.
Para obtermos uma compreensão clara do crescimento exponencial, vamos comparar o crescimento exponencial com o crescimento linear. Vamos construir duas funções. A primeira função é exponencial. Começaremos com uma entrada de\(0\) e aumentaremos cada entrada em\(1\). Vamos dobrar as saídas consecutivas correspondentes. A segunda função é linear. Começaremos com uma entrada de\(0\) e aumentaremos cada entrada em\(1\). Adicionaremos\(2\) às saídas consecutivas correspondentes (Tabela\(\PageIndex{1}\)).
A partir da Tabela,\(\PageIndex{1}\) podemos inferir que, para essas duas funções, o crescimento exponencial supera o crescimento linear.
- O crescimento exponencial se refere ao valor original da faixa de aumentos na mesma porcentagem em incrementos iguais encontrados no domínio.
- O crescimento linear se refere ao valor original da faixa de aumentos na mesma quantidade em incrementos iguais encontrados no domínio.
| \(x\) | \(f(x)=2^x\) | \(g(x)=2x\) |
|---|---|---|
| \ (x\)” style="alinhamento vertical: médio; ">0 | \ (f (x) =2^x\)” style="alinhamento vertical:médio; ">1 | \ (g (x) =2x\)” style="alinhamento vertical:médio; ">0 |
| \ (x\)” style="alinhamento vertical: médio; ">1 | \ (f (x) =2^x\)” style="alinhamento vertical:médio; ">2 | \ (g (x) =2x\)” style="alinhamento vertical:médio; ">2 |
| \ (x\)” style="alinhamento vertical: médio; ">2 | \ (f (x) =2^x\)” style="alinhamento vertical:médio; ">4 | \ (g (x) =2x\)” style="alinhamento vertical:médio; ">4 |
| \ (x\)” style="alinhamento vertical: médio; ">3 | \ (f (x) =2^x\)” style="alinhamento vertical:médio; ">8 | \ (g (x) =2x\)” style="alinhamento vertical:médio; ">6 |
| \ (x\)” style="alinhamento vertical: médio; ">4 | \ (f (x) =2^x\)” style="alinhamento vertical:médio; ">16 | \ (g (x) =2x\)” style="alinhamento vertical:médio; ">8 |
| \ (x\)” style="alinhamento vertical: médio; ">5 | \ (f (x) =2^x\)” style="alinhamento vertical:médio; ">32 | \ (g (x) =2x\)” style="alinhamento vertical:médio; ">10 |
| \ (x\)” style="alinhamento vertical: médio; ">6 | \ (f (x) =2^x\)” style="alinhamento vertical:médio; ">64 | \ (g (x) =2x\)” style="alinhamento vertical:médio; ">12 |
Aparentemente, a diferença entre “a mesma porcentagem” e “a mesma quantidade” é bastante significativa. Para crescimento exponencial, em incrementos iguais, a taxa de variação multiplicativa constante resultou na duplicação da saída sempre que a entrada aumentava em um. Para o crescimento linear, a taxa aditiva constante de variação em incrementos iguais resultou na adição\(2\) à saída sempre que a entrada era aumentada em um.
A forma geral da função exponencial é\(f(x)=ab^x\), onde\(a\) é qualquer número diferente de zero,\(b\) é um número real positivo não igual\(1\) a.
- Se\(b>1\), a função cresce a uma taxa proporcional ao seu tamanho.
- Se\(0<b<1\), a função decai a uma taxa proporcional ao seu tamanho.
Vamos dar uma olhada na função\(f(x)=2^x\) do nosso exemplo. Criaremos uma tabela (Tabela\(\PageIndex{2}\)) para determinar as saídas correspondentes em um intervalo no domínio de\(−3\) até\(3\).
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(f(x)=2^x\) | \(2^{−3}=\dfrac{1}{8}\) | \(2^{−2}=\dfrac{1}{4}\) | \(2^{−1}=\dfrac{1}{2}\) | \(2^0=1\) | \(2^1=2\) | \(2^2=4\) | \(2^3=8\) |
Vamos examinar o gráfico de\(f\) plotando os pares ordenados da Tabela\(\PageIndex{2}\) e, em seguida, fazer algumas observações\(\PageIndex{1}\).
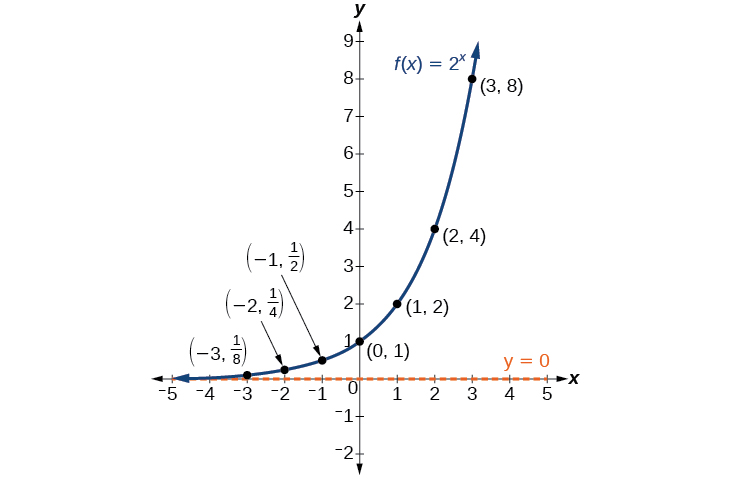
Vamos definir o comportamento do gráfico da função exponencial\(f(x)=2^x\) e destacar algumas de suas principais características.
- o domínio é\((−\infty,\infty)\),
- o alcance é\((0,\infty)\),
- como\(x\rightarrow \infty\)\(f(x)\rightarrow \infty\),
- como\(x\rightarrow −\infty\)\(f(x)\rightarrow 0\),
- \(f(x)\)está sempre aumentando,
- o gráfico de nunca\(f(x)\) tocará o eixo x porque a base dois elevada a qualquer expoente nunca tem o resultado de zero.
- \(y=0\)é a assíntota horizontal.
- o intercepto y é\(1\).
Para qualquer número real\(x\), uma função exponencial é uma função com a forma
\[f(x)=ab^x\]
onde
- \(a\)é um número real diferente de zero chamado valor inicial e
- \(b\)é qualquer número real positivo como esse\(b≠1\).
- O domínio de\(f\) são todos números reais.
- O intervalo de\(f\) é todo um número real positivo se\(a>0\).
- O intervalo de\(f\) é todo números reais negativos se\(a<0\).
- O intercepto y é\((0,a)\), e a assíntota horizontal é\(y=0\).
Quais das seguintes equações não são funções exponenciais?
- \(f(x)=4^{3(x−2)}\)
- \(g(x)=x^3\)
- \(h(x)=\left(\dfrac{1}{3}\right)^x\)
- \(j(x)=(−2)^x\)
Solução
Por definição, uma função exponencial tem uma constante como base e uma variável independente como expoente. Portanto,\(g(x)=x^3\) não representa uma função exponencial porque a base é uma variável independente. Na verdade,\(g(x)=x^3\) é uma função de energia.
Lembre-se de que a base\(b\) de uma função exponencial é sempre uma constante positiva\(b≠1\) e. Assim,\(j(x)={(−2)}^x\) não representa uma função exponencial porque a base,\(−2\), é menor que\(0\).
Quais das seguintes equações representam funções exponenciais?
- \(f(x)=2x^2−3x+1\)
- \(g(x)={0.875}^x\)
- \(h(x)=1.75x+2\)
- \(j(x)={1095.6}^{−2x}\)
- Responda
-
\(g(x)={0.875}^x\)e\(j(x)={1095.6}^{−2x}\) representam funções exponenciais.
Cálculo de funções exponenciais
Lembre-se de que a base de uma função exponencial deve ser um número real positivo diferente de\(1\) .Por que limitamos a base bb a valores positivos? Para garantir que as saídas sejam números reais. Observe o que acontece se a base não for positiva:
- Deixe\(b=−9\)\(x=\dfrac{1}{2}\) e. Então\(f(x)=f\left(\dfrac{1}{2}\right)={(−9)}^{\dfrac{1}{2}}=\sqrt{−9}\), o que não é um número real.
Por que limitamos a base a valores positivos diferentes de\(1\)? Porque a base\(1\) resulta na função constante. Observe o que acontece se a base for\(1\):
- Deixe\(b=1\). Então,\(f(x)=1^x=1\) para qualquer valor de\(x\).
Para calcular uma função exponencial com a forma\(f(x)=b^x\), simplesmente substituímos\(x\) pelo valor dado e calculamos a potência resultante. Por exemplo:
Deixe\(f(x)=2^x\). O que é\(f(3)\)?
\[\begin{align*} f(x)&= 2^x\\ f(3)&= 2^3 \qquad \text{Substitute } x=3\\ &= 8 \qquad \text{Evaluate the power} \end{align*}\]
Para avaliar uma função exponencial com uma forma diferente da forma básica, é importante seguir a ordem das operações. Por exemplo:
Deixe\(f(x)=30{(2)}^x\). O que é\(f(3)\)?
\[\begin{align*} f(x)&= 30{(2)}^x\\ f(3)&= 30{(2)}^3 \qquad \text{Substitute } x=3\\ &= 30(8) \qquad \text{Simplify the power first}\\ &= 240 \qquad \text{Multiply} \end{align*}\]
Observe que, se a ordem das operações não fosse seguida, o resultado estaria incorreto:
\[f(3)=30{(2)}^3≠{60}^3=216,000 \nonumber\]
Deixe\(f(x)=5{(3)}^{x+1}\). Avalie\(f(2)\) sem usar uma calculadora.
Solução
Siga a ordem das operações. Certifique-se de prestar atenção aos parênteses.
\[\begin{align*} f(x)&= 5{(3)}^{x+1}\\ f(2)&= 5{(3)}^{2+1} \qquad \text{Substitute } x=2\\ &= 5{(3)}^3 \qquad \text{Add the exponents}\\ &= 5(27) \qquad \text{Simplify the power}\\ &= 135 \qquad \text{Multiply} \end{align*}\]
Deixe\(f(x)=8{(1.2)}^{x−5}\). Avalie\(f(3)\) usando uma calculadora. Arredonde para quatro casas decimais.
- Responda
-
\(5.5556\)
Definindo o crescimento exponencial
Como a produção de funções exponenciais aumenta muito rapidamente, o termo “crescimento exponencial” é frequentemente usado na linguagem cotidiana para descrever qualquer coisa que cresça ou aumente rapidamente. No entanto, o crescimento exponencial pode ser definido com mais precisão em um sentido matemático. Se a taxa de crescimento for proporcional à quantidade presente, a função modela o crescimento exponencial.
Uma função que modela o crescimento exponencial cresce em uma taxa proporcional à quantidade presente. Para qualquer número real\(x\) e qualquer número real positivo\(a\) e\(b\) tal que\(b≠1\), uma função de crescimento exponencial tem a forma
\[f(x)=ab^x\]
onde
- \(a\)é o valor inicial ou inicial da função.
- \(b\)é o fator de crescimento ou multiplicador de crescimento por unidade\(x\).
Em termos mais gerais, temos uma função exponencial, na qual uma base constante é elevada a um expoente variável. Para diferenciar entre funções lineares e exponenciais, vamos considerar duas empresas, A e B. A empresa A tem\(100\) lojas e se expande abrindo\(50\) novas lojas por ano, então seu crescimento pode ser representado pela função\(A(x)=100+50x\). A empresa B tem\(100\) lojas e se expande aumentando o número de lojas a\(50\%\) cada ano, para que seu crescimento possa ser representado pela função\(B(x)=100{(1+0.5)}^x\).
Alguns anos de crescimento dessas empresas são ilustrados na Tabela\(\PageIndex{3}\).
| Ano,\(x\) | Lojas, Empresa A | Lojas, Empresa B |
|---|---|---|
| \ (x\) ">\(0\) | \(100+50(0)=100\) | \(100{(1+0.5)}^0=100\) |
| \ (x\) ">\(1\) | \(100+50(1)=150\) | \(100{(1+0.5)}^1=150\) |
| \ (x\) ">\(2\) | \(100+50(2)=200\) | \(100{(1+0.5)}^2=225\) |
| \ (x\) ">\(3\) | \(100+50(3)=250\) | \(100{(1+0.5)}^3=337.5\) |
| \ (x\) ">\(x\) | \(A(x)=100+50x\) | \(B(x)=100{(1+0.5)}^x\) |
Os gráficos que comparam o número de lojas de cada empresa em um período de cinco anos são mostrados na Figura\(\PageIndex{2}\). Podemos ver que, com o crescimento exponencial, o número de lojas aumenta muito mais rapidamente do que com o crescimento linear.
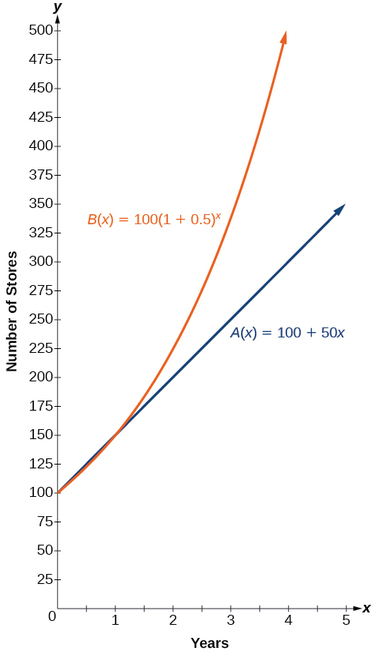
Observe que o domínio para ambas as funções é\([0,\infty)\), e o intervalo para ambas as funções é\([100,\infty)\). Depois do primeiro ano, a empresa B sempre tem mais lojas do que a empresa A.
Agora vamos voltar nossa atenção para a função que representa o número de lojas da Empresa\(B\),\(B(x)=100{(1+0.5)}^x\). Nessa função exponencial,\(100\) representa o número inicial de lojas,\(0.50\) representa a taxa de crescimento e\(1+0.5=1.5\) representa o fator de crescimento. Generalizando ainda mais, podemos escrever essa função como\(B(x)=100{(1.5)}^x\), onde\(100\) está o valor inicial,\(1.5\) é chamada de base e\(x\) é chamada de expoente.
No início desta seção, aprendemos que a população da Índia era de cerca de\(1.25\) bilhões no ano de 2013, com uma taxa de crescimento anual de cerca de\(1.2\%\). Essa situação é representada pela função de crescimento\(P(t)=1.25{(1.012)}^t\), onde\(t\) está o número de anos desde 2013. Até o milésimo mais próximo, qual será a população da Índia em 2031?
Solução
Para estimar a população em 2031, avaliamos os modelos para\(t=18\), porque 2031 é\(18\) anos após 2013. Arredondando para o milésimo mais próximo,
\[P(18)=1.25{(1.012)}^{18}≈1.549 \nonumber\]
Haverá cerca\(1.549\) de bilhões de pessoas na Índia no ano de 2031.
A população da China era de cerca de\(1.39\) bilhões no ano de 2013, com uma taxa de crescimento anual de cerca de\(0.6\%\). Essa situação é representada pela função de crescimento\(P(t)=1.39{(1.006)}^t\), onde\(t\) está o número de anos desde 2013. Até o milésimo mais próximo, qual será a população da China para o ano de 2031? Como isso se compara à previsão populacional que fizemos para a Índia em Example\(\PageIndex{3}\)?
- Responda
-
Cerca\(1.548\) de bilhões de pessoas; até o ano de 2031, a população da Índia excederá a da China em cerca de\(0.001\) bilhões ou\(1\) milhões de pessoas.
Encontrando equações de funções exponenciais
Nos exemplos anteriores, recebemos uma função exponencial, que depois avaliamos para uma determinada entrada. Às vezes, recebemos informações sobre uma função exponencial sem conhecê-la explicitamente. Devemos usar as informações para primeiro escrever a forma da função, depois determinar as constantes\(a, a\) e avaliar a função.\(b, b\)
- Se um dos pontos de dados tiver o formato\((0,a)\), então será\(a\) o valor inicial. Usando\(a\), substitua o segundo ponto na equação\(f(x)=a{(b)}^x\) e resolva por\(b\).
- Se nenhum dos pontos de dados tiver a forma\((0,a)\), substitua os dois pontos em duas equações pelo formulário\(f(x)=a{(b)}^x\). Resolva o sistema resultante de duas equações em duas incógnitas para encontrar\(a\)\(b\) e.
- Usando o\(a\) e\(b\) encontrado nas etapas acima, escreva a função exponencial no formulário\(f(x)=a{(b)}^x\).
Em 2006, os\(80\) cervos foram introduzidos em um refúgio de vida selvagem. Em 2012, a população se transformou em\(180\) veados. A população estava crescendo exponencialmente. Escreva uma função algébrica\(N(t)\) representando a população\((N)\) de cervos ao longo do tempo\(t\).
Solução
Deixamos nossa variável independente\(t\) ser o número de anos após 2006. Assim, as informações fornecidas no problema podem ser escritas como pares de entrada-saída: (0, 80) e (6, 180). Observe que, ao escolher nossa variável de entrada para ser medida em anos após 2006, nos demos o valor inicial da função,\(a=80\). Agora podemos substituir o segundo ponto na equação\(N(t)=80b^t\) para encontrar\(b\):
\[\begin{align*} N(t)&= 80b^t\\ 180&= 80b^6 \qquad \text{Substitute using point } (6, 180)\\ \dfrac{9}{4}&= b^6 \qquad \text{Divide and write in lowest terms}\\ b&= {\left (\dfrac{9}{4} \right )}^{\tfrac{1}{6}} \qquad \text{Isolate b using properties of exponents}\\ b&\approx 1.1447 \qquad \text{Round to 4 decimal places} \end{align*}\]
Salvo indicação em contrário, não arredonde nenhum cálculo intermediário. Em seguida, arredonde a resposta final para quatro lugares no restante desta seção.
O modelo exponencial para a população de cervos é\(N(t)=80{(1.1447)}^t\). (Observe que essa função exponencial modela o crescimento de curto prazo. À medida que as entradas aumentam, a saída fica cada vez maior, tanto que o modelo pode não ser útil a longo prazo.)
Podemos representar graficamente nosso modelo para observar o crescimento populacional de veados no refúgio ao longo do tempo. Observe que o gráfico na Figura\(\PageIndex{3}\) passa pelos pontos iniciais dados no problema,\((0, 80)\)\((6, 180)\) e. Também podemos ver que o domínio da função é\([0,\infty)\), e o intervalo da função é\([80,\infty)\).
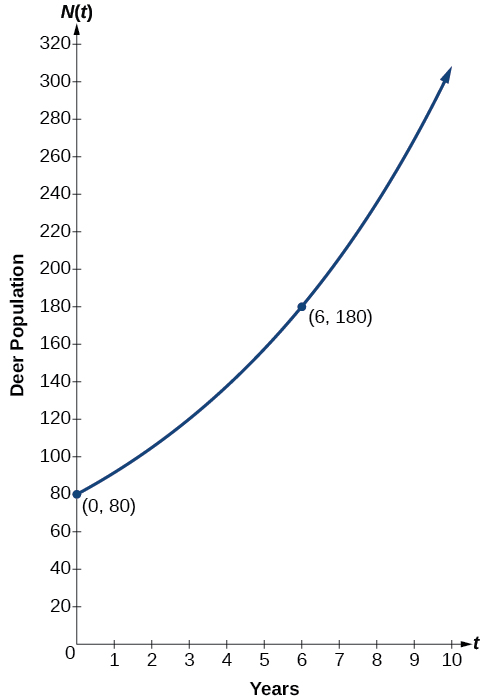
A população de lobos está crescendo exponencialmente. Em 2011,\(129\) os lobos foram contados. Em 2013, a população havia atingido\(236\) os lobos. Quais dois pontos podem ser usados para derivar uma equação exponencial modelando essa situação? Escreva a equação representando a população\(N\) de lobos ao longo do tempo\(t\).
- Responda
-
\((0,129)\)e\((2,236)\);\(N(t)=129{(1.3526)}^t\)
Encontre uma função exponencial que passe pelos pontos\((−2,6)\)\((2,1)\) e.
Solução
Como não temos o valor inicial, substituímos os dois pontos em uma equação da forma e\(f(x)=ab^x\), em seguida, resolvemos o sistema por\(a\)\(b\) e.
- Substituindo\((−2,6)\) dá\(6=ab^{−2}\)
- Substituindo\((2,1)\) dá\(1=ab^2\)
Use a primeira equação para resolver\(a\) em termos de\(b\):
\[\begin{align*} 6&= ab^{-2}\\ \dfrac{6}{b^{-2}}&= a \qquad \text{Divide}\\ a&= 6b^2 \qquad \text{Use properties of exponents to rewrite the denominator} \end{align*}\]
Substitua a na segunda equação e resolva por\(b\):
\[\begin{align*} 1&= ab^{2}\\ 1&= 6b^2 b^2\\ &= 6b^4 \qquad \text{Substitute a}\\ b&= \left (\dfrac{1}{6} \right )^{\tfrac{1}{4}} \qquad \text{Round 4 decimal places rewrite the denominator}\\ b&\approx 0.6389 \end{align*}\]
Use o valor de\(b\) na primeira equação para resolver o valor de\(a\):
\[\begin{align*} a&= 6b^{2}\\ &\approx 6(0.6389)^2 \\ &\approx 2.4492 \end{align*}\]
Assim, a equação é\(f(x)=2.4492{(0.6389)}^x\).
Podemos representar graficamente nosso modelo para verificar nosso trabalho. Observe que o gráfico na Figura\(\PageIndex{4}\) passa pelos pontos iniciais dados no problema,\((−2, 6)\)\((2, 1)\) e. O gráfico é um exemplo de uma função de decaimento exponencial.
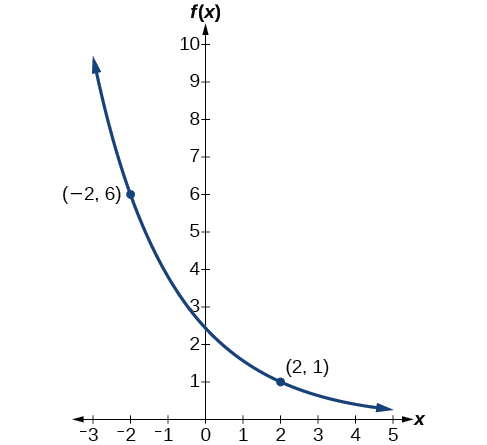
Dados os dois pontos\((1,3)\) e\((2,4.5)\), encontre a equação da função exponencial que passa por esses dois pontos.
- Responda
-
\(f(x)=2{(1.5)}^x\)
Sim, desde que os dois pontos estejam ambos acima do eixo x ou ambos abaixo do eixo x e tenham coordenadas x diferentes. Mas lembre-se de que também precisamos saber que o gráfico é, na verdade, uma função exponencial. Nem todo gráfico que parece exponencial é realmente exponencial. Precisamos saber que o gráfico é baseado em um modelo que mostra o mesmo percentual de crescimento com cada unidade de aumento, o que\(x\), em muitos casos do mundo real, envolve tempo.
- Primeiro, identifique dois pontos no gráfico. Escolha o\(y\) -intercept como um dos dois pontos sempre que possível. Tente escolher pontos tão distantes quanto possível para reduzir o erro de arredondamento.
- Se um dos pontos de dados for o\(y\) -intercept\((0,a)\), então será\(a\) o valor inicial. Usando\(a\), substitua o segundo ponto na equação\(f(x)=a{(b)}^x\) e resolva\(b\)
- Se nenhum dos pontos de dados tiver a forma\((0,a)\), substitua os dois pontos em duas equações pelo formulário\(f(x)=a{(b)}^x\). Resolva o sistema resultante de duas equações em duas incógnitas para encontrar\(a\)\(b\) e.
- Escreva a função exponencial,\(f(x)=a{(b)}^x\).
Encontre uma equação para a função exponencial representada graficamente na Figura\(\PageIndex{5}\).
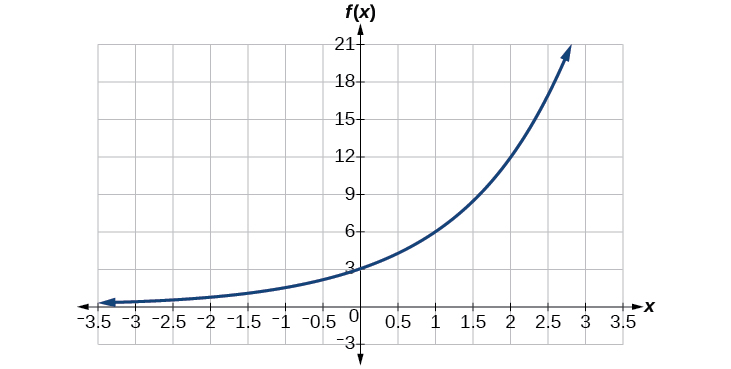
Solução
Podemos escolher o \(y\)intercepto -do gráfico,\((0,3)\), como nosso primeiro ponto. Isso nos dá o valor inicial,\(a=3\). Em seguida, escolha um ponto na curva a alguma distância\((0,3)\) que tenha coordenadas inteiras. Um desses pontos é\((2,12)\).
\[\begin{align*} y&= ab^x \qquad \text{Write the general form of an exponential equation}\\ y&= 3b^x \qquad \text{Substitute the initial value } 3 \text{ for } a\\ 12&= 3b^2 \qquad \text{Substitute in 12 for } y \text{ and } 2 \text{ for } x\\ 4&= b^2 \qquad \text{Divide by }3\\ b&= \pm 2 \qquad \text{Take the square root} \end{align*}\]
Porque nos restringimos a valores positivos de\(b\), usaremos\(b=2\). Substitua\(a\) e\(b\) na forma padrão para produzir a equação\(f(x)=3{(2)}^x\).
Encontre uma equação para a função exponencial representada graficamente na Figura\(\PageIndex{6}\).
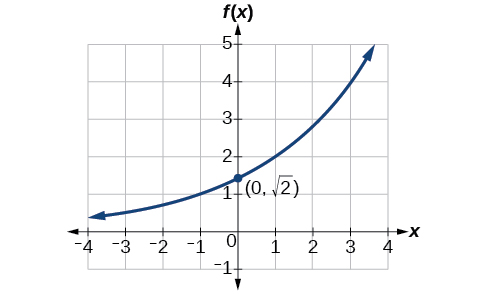
- Responda
-
\(f(x)=\sqrt{2}{(\sqrt{2})}^x\). As respostas podem variar devido a um erro de arredondamento. A resposta deve estar muito próxima de\(1.4142{(1.4142)}^x\).
- Pressione [STAT].
- Limpe todas as entradas existentes nas colunas L1 ou L2.
- Em L1, insira as coordenadas x fornecidas.
- Em L2, insira as coordenadas y correspondentes.
- Pressione [STAT] novamente. Cursor para a direita até CALC, role para baixo até ExpReg (Regressão Exponencial) e pressione [ENTER].
- A tela exibe os valores de a e b na equação exponencial\(y=a⋅b^x\).
Use uma calculadora gráfica para encontrar a equação exponencial que inclui os pontos\((2,24.8)\)\((5,198.4)\) e.
Solução
Siga as diretrizes acima. Primeiro pressione [STAT], [EDIT], [1: Editar...] e limpe as listas L1 e L2. Em seguida, na coluna L1, insira as\(x\) coordenadas -,\(2\)\(5\) e. Faça o mesmo na coluna L2 para as\(y\) coordenadas -,\(24.8\)\(198.4\) e.
Agora pressione [STAT], [CALC], [0: ExpReg] e pressione [ENTER]. Os valores serão exibidos\(a=6.2\) e\(b=2\) serão exibidos. A equação exponencial é\(y=6.2⋅2^x\).
Use uma calculadora gráfica para encontrar a equação exponencial que inclui os pontos\((3, 75.98)\)\((6, 481.07)\) e.
- Responda
-
\(y≈12⋅{1.85}^x\)
Aplicação da fórmula de juros compostos
Os instrumentos de poupança nos quais os lucros são continuamente reinvestidos, como fundos mútuos e contas de aposentadoria, usam juros compostos. O termo composição se refere aos juros auferidos não apenas sobre o valor original, mas sobre o valor acumulado da conta.
A taxa percentual anual (APR) de uma conta, também chamada de taxa nominal, é a taxa de juros anual obtida por uma conta de investimento. O termo nominal é usado quando a composição ocorre várias vezes, exceto uma vez por ano. Na verdade, quando os juros são compostos mais de uma vez por ano, a taxa de juros efetiva acaba sendo maior que a taxa nominal! Essa é uma ferramenta poderosa para investir.
Podemos calcular os juros compostos usando a fórmula de juros compostos, que é uma função exponencial das variáveis tempo\(t\)\(P\)\(APR\)\(r\), principal e número de períodos compostos em um ano\(n\):
\[A(t)=P{\left (1+\dfrac{r}{n} \right )}^{nt} \nonumber\]
Por exemplo, observe a Tabela\(\PageIndex{4}\), que mostra o resultado do investimento\($1,000\) em\(10\%\) um ano. Observe como o valor da conta aumenta à medida que a frequência de composição aumenta.
| Frequência | Valor após o\(1\) ano |
|---|---|
| Anualmente | \ (1\) ano">\($1100\) |
| Semestralmente | \ (1\) ano">\($1102.50\) |
| Trimestral | \ (1\) ano">\($1103.81\) |
| Mensalmente | \ (1\) ano">\($1104.71\) |
| Diariamente | \ (1\) ano">\($1105.16\) |
Os juros compostos podem ser calculados usando a fórmula
\[A(t)=P{\left (1+\dfrac{r}{n} \right )}^{nt}\]
onde
- \(A(t)\)é o valor da conta,
- \(t\)é medido em anos,
- \(P\)é o valor inicial da conta, geralmente chamado de principal, ou, mais geralmente, valor presente,
- \(r\)é a taxa anual percentual (APR) expressa como decimal, e
- \(n\)é o número de períodos de composição em um ano.
Se investirmos\($3,000\) em uma conta de investimento pagando\(3\%\) juros compostos trimestralmente, quanto valerá a conta em\(10\) anos?
Solução
Porque estamos começando com\($3,000\),\(P=3000\). Nossa taxa de juros é\(3\%\), então\(r = 0.03\). Como estamos compondo trimestralmente, estamos compondo\(4\) vezes por ano, então\(n=4\). Queremos saber o valor da conta em\(10\) anos, então estamos procurando\(A(10)\), o valor quando\(t = 10\).
\[\begin{align*} A(t)&= P{\left (1+\dfrac{r}{n} \right )}^{nt} \qquad \text{Use the compound interest formula}\\ A(10)&= 3000{\left (1+\dfrac{0.03}{4} \right )}^{(4)\cdot (10)} \qquad \text{Substitute using given values}\\ &\approx \$4045.05 \qquad \text{Round to two decimal places} \end{align*}\]
A conta valerá cerca\($4,045.05\) de\(10\) anos.
Um investimento inicial\($100,000\) de\(12\%\) juros é composto semanalmente (use\(52\) semanas em um ano). Quanto valerá o investimento em\(30\) anos?
- Responda
-
sobre\($3,644,675.88\)
O Plano 529 é um plano de poupança universitária que permite que parentes invistam dinheiro para pagar as futuras mensalidades universitárias de uma criança; a conta cresce isenta de impostos. Lily quer abrir uma conta 529 para sua nova neta e quer que a conta cresça ao\($40,000\) longo dos\(18\) anos. Ela acredita que a conta ganhará um valor\(6\%\) composto semestralmente (duas vezes por ano). Até o dólar mais próximo, quanto Lily precisará investir na conta agora?
Solução
A taxa de juros nominal é\(6\%\), então\(r=0.06\). Os juros são compostos duas vezes por ano, então\(k=2\).
Queremos encontrar o investimento inicial\(P\), necessário para que o valor da conta valha\($40,000\) em\(18\) anos. Substitua os valores fornecidos na fórmula de juros compostos e resolva\(P\).
\[\begin{align*} A(t)&= P{\left (1+\dfrac{r}{n} \right )}^{nt} \qquad \text{Use the compound interest formula}\\ 40,000&= P{\left (1+\dfrac{0.06}{2} \right )}^{2(18)} \qquad \text{Substitute using given values } A, r, n, t\\ 40,000&= P{(1.03)}^{36} \qquad \text{Simplify}\\ \dfrac{40,000}{ {(1.03)}^{36} }&= P \qquad \text{Isolate } P\\ P&\approx \$13,801 \qquad \text{Divide and round to the nearest dollar} \end{align*}\]
Lily precisará investir\($13,801\) para ter\($40,000\) em\(18\) anos.
Consulte o exemplo\(\PageIndex{9}\). Até o dólar mais próximo, quanto Lily precisaria investir se a conta fosse composta trimestralmente?
- Responda
-
\($13,693\)
Avaliando funções com o Base\(e\)
Como vimos anteriormente, o valor ganho em uma conta aumenta à medida que a frequência de composição aumenta. A tabela\(\PageIndex{5}\) mostra que o aumento da composição anual para a semestral é maior do que o aumento da composição mensal para a diária. Isso pode nos levar a perguntar se esse padrão continuará.
Examine o valor do\($1\) investimento em\(100\%\) juros por\(1\) ano, composto em várias frequências, listado na Tabela\(\PageIndex{5}\).
| Frequência | \(A(t)={\left (1+\dfrac{1}{n} \right )}^n\) | Valor |
|---|---|---|
| Anualmente | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="alinhamento vertical: meio; ">\({\left (1+\dfrac{1}{1} \right )}^1\) | \($2\) |
| Semestralmente | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="alinhamento vertical: meio; ">\({\left (1+\dfrac{1}{2} \right )}^2\) | \($2.25\) |
| Trimestral | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="alinhamento vertical: meio; ">\({\left (1+\dfrac{1}{4} \right )}^4\) | \($2.441406\) |
| Mensalmente | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="alinhamento vertical: meio; ">\({\left (1+\dfrac{1}{12} \right )}^{12}\) | \($2.613035\) |
| Diariamente | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="alinhamento vertical: meio; ">\({\left (1+\dfrac{1}{365} \right )}^{365}\) | \($2.714567\) |
| A cada hora | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="alinhamento vertical: meio; ">\({\left (1+\dfrac{1}{8760} \right )}^{8760}\) | \($2.718127\) |
| Uma vez por minuto | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="alinhamento vertical: meio; ">\({\left (1+\dfrac{1}{525600} \right )}^{525600}\) | \($2.718279\) |
| Uma vez por segundo | \ (A (t) = {\ left (1+\ dfrac {1} {n}\ right)} ^n\)” style="alinhamento vertical: meio; ">\({\left (1+\dfrac{1}{31536000} \right )}^{31536000}\) | \($2.718282\) |
Esses valores parecem estar se aproximando de um limite à medida que\(n\) aumentam sem limite. Na verdade, à medida\(n\) que se torna cada vez maior, a expressão\({\left (1+\dfrac{1}{n} \right )}^n\) se aproxima de um número usado com tanta frequência em matemática que tem seu próprio nome: a letra\(e\). Esse valor é um número irracional, o que significa que sua expansão decimal continua para sempre sem se repetir. Sua aproximação com seis casas decimais é mostrada abaixo.
A letra\(e\) representa o número irracional
\[{\left (1+\dfrac{1}{n} \right )}^n\]
à medida que\(n\) aumenta sem limite
A letra\(e\) é usada como base para muitos modelos exponenciais do mundo real. Para trabalhar com base\(e\), usamos a aproximação,\(e≈2.718282\). A constante foi nomeada pelo matemático suíço Leonhard Euler (1707—1783), que primeiro investigou e descobriu muitas de suas propriedades.
Calcule\(e^{3.14}\). Arredonde para cinco casas decimais.
Solução
Em uma calculadora, pressione o botão rotulado\([e^x]\). A janela mostra\([e {}^( ]\). Digite\(3.14\) e feche o parêntese,\([)]\). Pressione [ENTER]. Arredondando para\(5\) casas decimais,\(e^{3.14}≈23.10387\). Cuidado: muitas calculadoras científicas têm um botão “Exp”, que é usado para inserir números em notação científica. Não é usado para encontrar poderes de\(e\).
Use uma calculadora para encontrar\(e^{−0.5}\). Arredonde para cinco casas decimais.
- Responda
-
\(e^{−0.5}≈0.60653\)
Investigando o crescimento contínuo
Até agora, trabalhamos com bases racionais para funções exponenciais. Para a maioria dos fenômenos do mundo real, entretanto,\(e\) é usado como base para funções exponenciais. Os modelos exponenciais que usam\(e\) como base são chamados de modelos contínuos de crescimento ou decaimento. Vemos esses modelos em finanças, ciência da computação e na maioria das ciências, como física, toxicologia e dinâmica de fluidos.
Para todos os números\(t\) reais e todos os números positivos\(a\) e\(r\), o crescimento ou declínio contínuo é representado pela fórmula
\[A(t)=ae^{rt}\]
onde
- \(a\)é o valor inicial,
- \(r\)é a taxa de crescimento contínuo por unidade de tempo,
- \(t\)é o tempo decorrido.
Se\(r>0\) sim, então a fórmula representa crescimento contínuo. Se\(r<0\), então a fórmula representa decaimento contínuo.
Para aplicativos de negócios, a fórmula de crescimento contínuo é chamada de fórmula de composição contínua e assume a forma
\[A(t)=Pe^{rt}\]
onde
- \(P\)é o principal ou o investido inicial,
- \(r\)é o crescimento ou a taxa de juros por unidade de tempo,
- \(t\)é o período ou prazo do investimento.
- Use as informações do problema para determinar\(a\) o valor inicial da função.
- Use as informações do problema para determinar a taxa de crescimento\(r\).
- Se o problema se refere ao crescimento contínuo, então\(r>0\).
- Se o problema se referir à deterioração contínua, então\(r<0\).
- Use as informações do problema para determinar a hora\(t\).
- Substitua as informações fornecidas pela fórmula de crescimento contínuo e resolva\(A(t)\).
Uma pessoa investiu\($1,000\) em uma conta ganhando um valor nominal\(10\%\) por ano composto continuamente. Quanto estava na conta no final de um ano?
Solução
Como o valor da conta está crescendo, esse é um problema contínuo de agravamento da taxa de crescimento\(r=0.10\). O investimento inicial foi\($1,000\), então\(P=1000\). Usamos a fórmula de composição contínua para encontrar o valor após o\(t=1\) ano:
\[\begin{align*} A(t)&= Pe^{rt} \qquad \text{Use the continuous compounding formula}\\ &= 1000{(e)}^{0.1} \qquad \text{Substitute known values for } P, r, t\\ &\approx 1105.17 \qquad \text{Use a calculator to approximate} \end{align*}\]
A conta vale\($1,105.17\) depois de um ano.
Uma pessoa investe\($100,000\) com\(12\%\) juros nominais por ano compostos continuamente. Qual será o valor do investimento em\(30\) anos?
- Responda
-
\($3,659,823.44\)
\(Radon-222\)decai a uma taxa contínua de\(17.3\%\) por dia. Quanto tempo durará\(100 mg\) a\(Radon-222\) decadência em\(3\) dias?
Solução
Como a substância está em decomposição, a taxa,\(17.3\%\), é negativa. Então,\(r = −0.173\). A quantidade inicial de\(Radon-222\) foi de\(100\) mg, então\(a=100\). Usamos a fórmula de decaimento contínuo para encontrar o valor após\(t=3\) dias:
\[\begin{align*} A(t)&= ae^{rt} \qquad \text{Use the continuous growth formula}\\ &= 100e6{-0.173(3)} \qquad \text{Substitute known values for } a, r, t\\ &\approx 59.5115 \qquad \text{Use a calculator to approximate} \end{align*}\]
Então,\(59.5115\) meu filho\(Radon-222\) permanecerá.
Usando os dados em Example\(\PageIndex{12}\), quanto\(Radon-222\) restará após um ano?
- Responda
-
\(3.77E-26\)(Esta é a notação da calculadora para o número escrito como\(3.77×10^{−26}\) na notação científica. Embora a saída de uma função exponencial nunca seja zero, esse número é tão próximo de zero que, para todos os propósitos práticos, podemos aceitar zero como resposta.)
Acesse esses recursos on-line para obter instruções e práticas adicionais com funções exponenciais.
- Função de crescimento exponencial
- Juros compostos
Equações-chave
| definição da função exponencial | \(f(x)=b^x\), onde\(b>0\),\(b≠1\) |
| definição de crescimento exponencial | \(f(x)=ab^x\), onde\(a>0\)\(b>0\),\(b≠1\) |
| fórmula de juros compostos |
\(A(t)=P{(1+\dfrac{r}{n})}^{nt}\), onde\(A(t)\) está o valor da conta no momento\(t\) \(t\)é o número de anos \(P\)é o investimento inicial, muitas vezes chamado de principal \(r\)é a taxa percentual anual (APR), ou taxa nominal \(n\)é o número de períodos de composição em um ano |
| fórmula de crescimento contínuo | \(A(t)=ae^{rt}\), onde\(t\) é o número de períodos unitários de crescimento\(a\) é a quantidade inicial (na fórmula de composição contínua, a é substituída por\(P\), o principal)\(e\) é a constante matemática,\(e≈2.718282\) |
Conceitos-chave
- Uma função exponencial é definida como uma função com uma constante positiva diferente de\(1\) elevada a um expoente variável. Veja o exemplo.
- Uma função é avaliada resolvendo em um valor específico. Veja o exemplo e o exemplo.
- Um modelo exponencial pode ser encontrado quando a taxa de crescimento e o valor inicial são conhecidos. Veja o exemplo.
- Um modelo exponencial pode ser encontrado quando os dois pontos de dados do modelo são conhecidos. Veja o exemplo.
- Um modelo exponencial pode ser encontrado usando dois pontos de dados do gráfico do modelo. Veja o exemplo.
- Um modelo exponencial pode ser encontrado usando dois pontos de dados do gráfico e uma calculadora. Veja o exemplo.
- O valor de uma conta a qualquer momento\(t\) pode ser calculado usando a fórmula de juros compostos quando o principal, a taxa de juros anual e os períodos compostos são conhecidos. Veja o exemplo.
- O investimento inicial de uma conta pode ser encontrado usando a fórmula de juros compostos quando o valor da conta, a taxa de juros anual, os períodos compostos e a vida útil da conta são conhecidos. Veja o exemplo.
- O número\(e\) é uma constante matemática frequentemente usada como base dos modelos de crescimento e decaimento exponenciais do mundo real. Sua aproximação decimal é\(e≈2.718282\).
- As calculadoras científicas e gráficas têm a chave\([ex]\) ou\([exp(x)]\) para calcular os poderes de\(e\). Veja o exemplo.
- Modelos contínuos de crescimento ou decaimento são modelos exponenciais que usam\(e\) como base. Modelos contínuos de crescimento e decaimento podem ser encontrados quando o valor inicial e a taxa de crescimento ou decaimento são conhecidos. Veja o exemplo e o exemplo.


