3.5: Dividindo polinômios

Last updated
Save as PDF

Page ID: 189229

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Use a divisão longa para dividir polinômios.
Use a divisão sintética para dividir polinômios.

O exterior do Lincoln Memorial em Washington, D.C., é um grande sólido retangular com comprimento$61.5$ metros (m), largura$40$ m e altura$30$ m.$^1$

Podemos encontrar facilmente o volume usando geometria elementar.

\[\begin{align*} V&=l \; {\cdot} \; w \; {\cdot} \; h \\ &=61.5 \; {\cdot} \; 40 \; {\cdot} \; 30 \\ &=73,800 \end{align*}\]

Portanto, o volume é de metros$73,800$ cúbicos ($m^3$).

alt — Figura$\PageIndex{1}$: Lincoln Memorial, Washington, D.C. (crédito: Ron Cogswell, Flickr)

Suponha que soubéssemos o volume, o comprimento e a largura. Poderíamos dividir para encontrar a altura.

\[\begin{align*} h&=\dfrac{V}{l{\cdot}w} \\&=\dfrac{73,800}{61.5{\cdot}40} \\ &=30 \end{align*}\]

Como podemos confirmar nas dimensões acima, a altura é de 30 m. Podemos usar métodos semelhantes para encontrar qualquer uma das dimensões que faltam. Também podemos usar o mesmo método se alguma ou todas as medidas contiverem expressões variáveis. Por exemplo, suponha que o volume de um sólido retangular seja dado pelo polinômio$3x^4−3x^3−33x^2+54x$. O comprimento do sólido é dado por$3x$; a largura é dada por$x−2$.

Para encontrar a altura do sólido, podemos usar a divisão polinomial, que é o foco desta seção.

Usando divisão longa para dividir polinômios

Estamos familiarizados com o algoritmo de divisão longa para aritmética comum. Começamos dividindo os dígitos do dividendo que têm o maior valor posicional. Dividimos, multiplicamos, subtraímos, incluímos o dígito na próxima posição de valor posicional e repetimos. Por exemplo, vamos dividir 178 por 3 usando a divisão longa.

$alt$

Outra forma de analisar a solução é como uma soma de partes. Isso deve parecer familiar, pois é o mesmo método usado para verificar a divisão na aritmética elementar.

\[\begin{align*} \text{dividend}&=(\text{divisor}{\cdot}\text{quotient})+\text{remainder} \\ 178&=(3{\cdot}59)+1 \\ &=177+1 \\ &=178\end{align*}\]

Chamamos isso de Algoritmo de Divisão e o discutiremos mais formalmente depois de analisar um exemplo.

A divisão de polinômios que contêm mais de um termo tem semelhanças com a divisão longa de números inteiros. Podemos escrever um dividendo polinomial como o produto do divisor e o quociente adicionado ao restante. Os termos da divisão polinomial correspondem aos dígitos (e valores posicionais) da divisão de números inteiros. Esse método nos permite dividir dois polinômios. Por exemplo, se fôssemos dividir$2x^3−3x^2+4x+5$$x+2$ usando o algoritmo de divisão longa, ficaria assim:

\ [\ require {enclose}\ begin {array} {rll}\ large x+2\ enclose {longdiv} {2x^3-3x^2+4x+5\ phantom {0}} &\ qquad &\ large\ text {Configurar o problema da divisão.}\\ [8pt]
\ large 2x^2\ hspace {5.45em} &\ qquad &\ large2x^3\ text {dividido por} x\ text {é} 2x^2.\\ [-3pt]
\ large x+2\ enclose { longdiv} {2x^3-3x^2+4x+5\ phantom {0}} &\ quad &\\ [8pt]
\ grande 2x^2\ hspace {5.45em} &\ qquad &\\ [-3pt]
\ grande x+2\ encerrar {longdiv} {2x^3-3x^2+4x+5\ phan tom {0}} &\ quad &\\ [-3pt]
\ large\ underline {-\ left (2x^3 + 4x^2\ right)}\ hspace {4.9em} & \ qquad &\ large\ text {Multiplique} x+2\ texto {por} 2x^2\ texto {e subtraia.}\\ [-3pt]
\ large -7x^2+4x\ hspace {2.8em} &\ qquad &\ large\ text {Diminua o próximo termo.}\\ [8pt]\ large 2x^2 - 7x

\ hspace {2.2x\ hspace {2.2.85em} &\ qquad &\ large -7x^2\ text {dividido por} x\ text {é} -7x.\\ [-3pt]
\ grande x+2\ encerrar {longdiv} {2x^3-3x^2+4x+5\ phantom {0}} &\ qquad &\\ [-3pt]
\ large\ sublinhado {-\ left (2x^3 + 4x^2\ right)}\ hspace {4,9em} e\ qq quad &\\ [-3pt]
\ large -7x^2+4x\ hspace {2,8em} &\ quad &\\ [-3pt]
\ large\ underline {-\ left (-7x^2 - 14x\ right)}\ hspace {2.0em} &\ qquad &\ large\ text {Multiply} x+2\ text {by} -7x.\\ [-3pt]
\ large 18x+5\ phantom {0} &\ qquad &\ large\ text {Subtraia e reduza o próximo termo}.\\ [8 pontos]

\ grande 2x^2 - 7x+18 &\ qquad &\ large 18x\ text {dividido por} x\ text {é} 18.\\ [-3pt]
\ large x+2\ enclose {longdiv} {2x^3-3x^2+4x+5\ phantom {0}} &\ qquad &\\ [-3pt]
\ large\ underline {-\ left (2x^3 + 4x^4x^4 2\ right)}\ hspace {4,9em} &\ qquad &\\ [-3pt]
\ large -7x^2+4x\ hspace {2,8 em} &\ qquad &\\ [-3pt]
\ large\ underline {-\ left (-7x^2 - 14x\ right)}\ hspace {2.0em} &\ qquad &\\ [-3pt]
\ large 18x+\ phantom {0} 5 &\ qquad &\\ [-3pt]
\ large\ sublinhado {-\ left (18x + 36\ direita)}\ hspace {-0,45em} &\ qquad &\ large\ texto {Multiplicar} x+2\ texto {por} 18.\\ [-3pt]
\ large -31 &\ qquad &\ large\ text {Subtrair.}\\ [8pt]
\ end {array}\ nonumber\]

Nós encontramos

\[\dfrac{2x^3−3x^2+4x+5}{x+2}=2x^2−7x+18−\dfrac{31}{x+2} \nonumber\]

\[ 2x^3−3x^2+4x+5=(x+2)(2x^2−7x+18)−31 \nonumber\]

Podemos identificar o dividendo, o divisor, o quociente e o restante.

Escrever o resultado dessa maneira ilustra o algoritmo de divisão.

O algoritmo de divisão

O Algoritmo de Divisão afirma que, dado um dividendo polinomial$f(x)$ e um divisor polinomial diferente de zero,$d(x)$ onde o grau de$d(x)$ é menor ou igual ao grau de$f(x)$, existem polinômios únicos$q(x)$ e$r(x)$ tais que

\[f(x)=d(x)q(x)+r(x)\]

$q(x)$é o quociente e$r(x)$ é o restante. O restante é igual a zero ou tem um grau estritamente menor que$d(x)$.

Se$r(x)=0$, então se$d(x)$ divide uniformemente em$f(x)$. Isso significa que, nesse caso, ambos$d(x)$ e$q(x)$ são fatores de$f(x)$.

Dado um polinômio e um binômio, use a divisão longa para dividir o polinômio pelo binômio

Configure o problema de divisão.
Determine o primeiro termo do quociente dividindo o termo principal do dividendo pelo termo principal do divisor.
Multiplique a resposta pelo divisor e escreva-a abaixo dos termos semelhantes do dividendo.
Subtraia o binômio inferior do binômio superior.
Reduza o próximo prazo do dividendo.
Repita as etapas de 2 a 5 até atingir o último prazo do dividendo.
Se o restante for diferente de zero, expresse como uma fração usando o divisor como denominador.

Exemplo$\PageIndex{1}$: Using Long Division to Divide a Second-Degree Polynomial

Divida$5x^2+3x−2$ por$x+1$.

Solução

$alt$

O quociente é$5x−2$. O restante é 0. Escrevemos o resultado como

\[\dfrac{5x^2+3x−2}{x+1}=5x−2 \nonumber\]

\[5x^2+3x−2=(x+1)(5x−2) \nonumber\]

Análise

Esse problema de divisão tinha um restante de 0. Isso nos diz que o dividendo é dividido igualmente pelo divisor e que o divisor é um fator do dividendo.

Exemplo$\PageIndex{2}$: Using Long Division to Divide a Third-Degree Polynomial

Divida$6x^3+11x^2−31x+15$ por$3x−2$.

Solução

\ [\ require {enclose}\ begin {array} {rll}
\ large 2x^2 +\ phantom {0} 5x-\ phantom {0} 7 &\ qquad &\ large 6x^3\ text {dividido por} 3x\ text {é} 2x^2.\\ [-3pt]
\ large 3x-2\ enclose {longdiv} {6x^2 ^3+11x^2-31x+15} &\ qquad &\\ [-3pt]
\ large\ sublinhado {-\ left (6x^3 - 4x^2 \ right)}\ hspace {5.8em} &\ qquad &\ large\ text {Multiplique} 3x-2\ texto {por} 2x^2.\\ [-3pt]
\ large 15x^2-31x\ hspace {3.0em} &\ qquad &\ large\ text {Subtrair. Anote o próximo termo.} 15x^2\ text {dividido por} 3x\ text {é} 5x.\\ [-3pt]
\ large\ underline {-\ left (15x^2 - 10x\ right)}\ hspace {2.5em} &\ qquad &\ large\ text {Multiply} 3x-2\ text {by} 5x.\\ [-3pt]
large -21x+15\ hspace {0.5em} &\ qquad &\ large\ text {Subtrair. Abaixe o próximo termo.} -21x\ text {dividido por} 3x\ text {is} -7.\\ [-3pt]
\ large\ underline {-\ left (-21x + 14\ right)}\ hspace {0.1em} &\ qquad &\ large\ text {Multiply} 3x-2\ text {by} -7.\\ [-3pt]
\ large 1\ hspace {0.5em} &\ quad &\ large\ text {Subtrair. O restante é 1.}\\ [8pt]
\ end {array}\ nonumber\]

Há um restante de 1. Podemos expressar o resultado da seguinte forma:

\[\dfrac{6x^3+11x^2−31x+15}{3x−2}=2x^2+5x−7+\dfrac{1}{3x−2} \nonumber\]

Análise

Podemos verificar nosso trabalho usando o algoritmo de divisão para reescrever a solução. Em seguida, multiplique.

\[(3x−2)(2x^2+5x−7)+1=6x^3+11x^2−31x+15 \nonumber\]

Observe que, ao escrevermos nosso resultado,

o dividendo é$6x^3+11x^2−31x+15$
o divisor é$3x−2$
o quociente é$2x^2+5x−7$
o restante é$1$

Experimente! $\PageIndex{2}$

Divida$16x^3−12x^2+20x−3$ por$4x+5$.

Solução: $4x^2−8x+15−\dfrac{78}{4x+5}$

Usando divisão sintética para dividir polinômios

Como vimos, a divisão longa de polinômios pode envolver muitas etapas e ser bastante complicada. A divisão sintética é um método abreviado de dividir polinômios para o caso especial de divisão por um fator linear cujo coeficiente principal é$1.$

Para ilustrar o processo, lembre-se do exemplo no início da seção.

Divida$2x^3−3x^2+4x+5$$x+2$ usando o algoritmo de divisão longa.

A forma final do processo ficou assim:

\ [\ require {enclose}\ begin {array} {rl}\ grande 2x^2 - 7x+18 &\\ [-3pt]
\ grande x+2\ encerrar {longdiv} {2x^3-3x^2+4x+5\ fantasma {0}} &\\ [-3pt]
\ large\ sublinhado {-\ left (2x^3 + 4+ x^2\ right)}\ hspace {4,9em} &\\ [-3pt]
\ large -7x^2+4x\ hspace {2,8em} &\\ [-3pt]
\ large\ underline {-\ left (-7x^2 - 14x\ right)}\ hspace {2.0em} &\\ [-3pt]
\ large 18x+\ phantom {0} 5 &\\ [-3pt]
\ large\ underline {-\ left (18x + 36\ right)}\ hspace {-0,45em} &\\ [-3pt]
\ large -31 &\\ [8 pontos]
\ end {array}\ nonumber \]

Há muita repetição na tabela. Se não escrevermos as variáveis, mas, em vez disso, alinharmos seus coeficientes em colunas sob o sinal de divisão e também eliminarmos os produtos parciais, já teremos uma versão mais simples de todo o problema.

$alt$

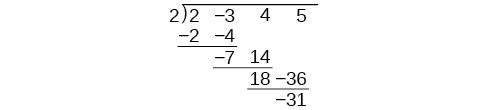
A divisão sintética traz essa simplificação ainda mais algumas etapas. Feche a mesa movendo cada uma das linhas para cima para preencher qualquer espaço vazio. Além disso, em vez de dividir por 2, como faríamos na divisão de números inteiros, multiplicando e subtraindo o produto médio, mudamos o sinal do “divisor” para —2, multiplicamos e adicionamos. O processo começa diminuindo o coeficiente inicial.

$alt$

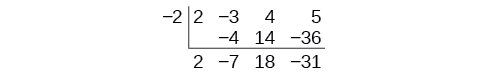
Em seguida, multiplicamos pelo “divisor” e adicionamos, repetindo esse processo coluna por coluna, até que não haja mais entradas. A linha inferior representa os coeficientes do quociente; a última entrada da linha inferior é o restante. Nesse caso, o quociente é$2x^2–7x+18$ e o restante é$–31.$ O processo ficará mais claro no Exemplo$\PageIndex{3}$.

Divisão sintética

A divisão sintética é um atalho que pode ser usado quando o divisor é um binômio no formulário$x−k$. Na divisão sintética, somente os coeficientes são usados no processo de divisão.

Dados dois polinômios, use a divisão sintética para dividir

Escreva$k$ para o divisor.
Escreva os coeficientes do dividendo.
Reduza o coeficiente de chumbo.
Multiplique o coeficiente de chumbo por$k$. Escreva o produto na próxima coluna.
Adicione os termos da segunda coluna.
Multiplique o resultado por$k$. Escreva o produto na próxima coluna.
Repita as etapas 5 e 6 para as colunas restantes.
Use os números inferiores para escrever o quociente. O número na última coluna é o restante e tem grau 0, o próximo número da direita tem grau 1, o próximo número da direita tem grau 2 e assim por diante.

Exemplo$\PageIndex{3}$: Using Synthetic Division to Divide a Second-Degree Polynomial

Use a divisão sintética para dividir$5x^2−3x−36$ por$x−3$.

Solução

Comece configurando a divisão sintética. Escreva$k$ e os coeficientes.

$alt$

Diminua o coeficiente de chumbo. Multiplique o coeficiente de chumbo por$k$.

$alt$

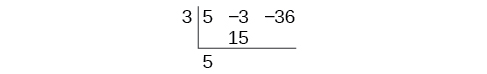
Continue adicionando os números na segunda coluna. Multiplique o número resultante por$k$ .Escreva o resultado na próxima coluna. Em seguida, adicione os números na terceira coluna.

$alt$

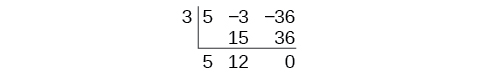
O resultado é$5x+12$. O restante é 0. Então$x−3$ é um fator do polinômio original.

Análise

Assim como na divisão longa, podemos verificar nosso trabalho multiplicando o quociente pelo divisor e adicionando o restante.

\[(x−3)(5x+12)+0=5x^2−3x−36 \nonumber\]

Exemplo$\PageIndex{4}$: Using Synthetic Division to Divide a Third-Degree Polynomial

Use a divisão sintética para dividir$4x^3+10x^2−6x−20$ por$x+2$.

Solução

O divisor binomial é$x+2$ assim$k=−2$. Adicione cada coluna, multiplique o resultado por —2 e repita até que a última coluna seja alcançada.

\ [\ large {\ begin {array} {c} -2\\\\\
\ end {array}} {\
begin {align*} &\\ [0pt]
& {\ begin {array} {r|}\\ [0pt]\\ [0pt]
\\ [0pt]\ end {array}}\\ [1pt]
&\\ [2pt] &\ end {align*}}\! \!
{\ begin {array} {rrrr}
1 & -1 e -11 e 18\\
& 2 & 2 & -18\\
\ hlinha 1 e 1 & -9 e 0
\ end {matriz}}
\ nonumber\]

O resultado é$4x^2+2x−10$.

O restante é 0. Portanto,$x+2$ é um fator de$4x^3+10x^2−6x−20$.

Análise

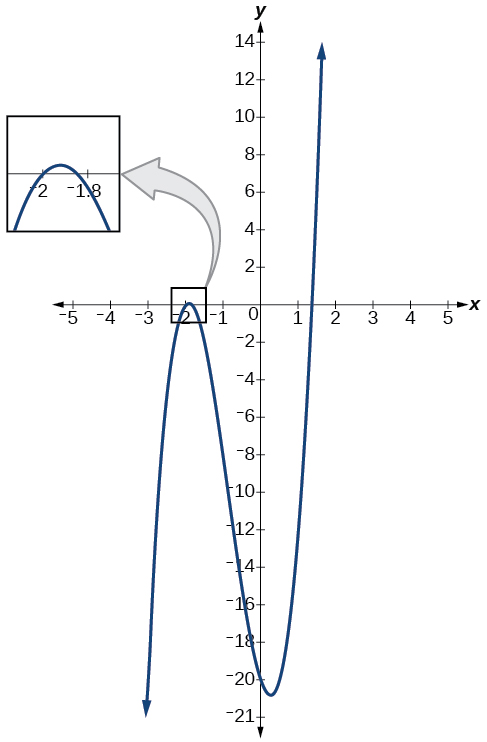
O gráfico da função polinomial$f(x)=4x^3+10x^2−6x−20$ na Figura$\PageIndex{2}$ mostra um zero em$x=k=−2$. Isso confirma que$x+2$ é um fator de$4x^3+10x^2−6x−20$.

Exemplo$\PageIndex{5}$: Using Synthetic Division to Divide a Fourth-Degree Polynomial

Use a divisão sintética para dividir$−9x^4+10x^3+7x^2−6$ por$x−1$.

Solução

Observe que não há$x$ termo. Usaremos um zero como coeficiente para esse termo.

\ [\ large {\ begin {array} {c} 1\\\\\
\ end {array}} {\
begin {align*} &\\ [0pt]
& {\ begin {array} {r|}\ [0pt]\\ [0pt]
\\ [0pt]\ end {array}}\\ [1pt]
&\\ [2pt] &\ end {align*}}\! \!
{\ begin {array} {rrrrr}
-9 e 10 e 7 e 0 &-6\\
& -9 e 1 e 8 e 8\\
\ hline -9 e 1 e 8 e 8 e 2
\ end {array}}
\ nonumber\]

O resultado é$−9x^3+x^2+8x+8+\dfrac{2}{x−1}$.

Experimente! $\PageIndex{3}$

Use a divisão sintética para dividir$3x^4+18x^3−3x+40$ por$x+7$.

Solução: $3x^3−3x^2+21x−150+\dfrac{1090}{x+7}$

Usando a divisão polinomial para resolver problemas de aplicação

A divisão polinomial pode ser usada para resolver uma variedade de problemas de aplicação envolvendo expressões para área e volume. Analisamos um aplicativo no início desta seção. Agora resolveremos esse problema no exemplo a seguir.

Exemplo$\PageIndex{6}$: Using Polynomial Division in an Application Problem

O volume de um sólido retangular é dado pelo polinômio$3x^4−3x^3−33x^2+54x$. O comprimento do sólido é dado por$3x$ e a largura é dada por$x−2$. Encontre a altura$h$ do sólido.

Solução

Existem algumas maneiras de abordar esse problema. Precisamos dividir a expressão do volume do sólido pelas expressões do comprimento e da largura. Vamos criar um esboço como na Figura$\PageIndex{3}$. Seja$h$ igual à altura da caixa.

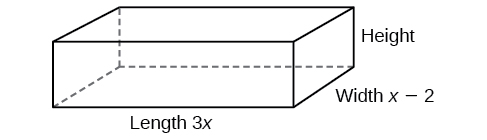
Agora podemos escrever uma equação substituindo os valores conhecidos na fórmula pelo volume de um sólido retangular.

\[\begin{align*} V&=l{\cdot}w{\cdot}h \\ 3x^4−3x^3−33x^2+54x&=3x{\cdot}(x−2){\cdot}h \end{align*}\]

Para resolver$h$, primeiro divida os dois lados por$3x$.

\[\dfrac{3x{\cdot}(x−2){\cdot}h}{3x}=\dfrac{3x^4−3x^3−33x^2+54x}{3x} \nonumber\]

\[(x-2)h=\dfrac{x^3-x^2-11x+18}{x-2} \nonumber\]

Agora resolva o$h$ uso da divisão sintética.

\[h=\dfrac{x^3−x^2−11x+18}{x−2} \nonumber\]

O quociente é$x^2+x−9$ e o restante é$0.$ A altura do sólido é$x^2+x−9$.

Experimente! $\PageIndex{4}$

A área de um retângulo é dada por$3x^3+14x^2−23x+6$. A largura do retângulo é dada por$x+6$. Encontre uma expressão para o comprimento do retângulo.

Solução: $3x^2−4x+1$

Equações-chave

algoritmo de divisão$f(x)=d(x)q(x)+r(x)$ onde$q(x){\neq}0$

Conceitos-chave

A divisão longa polinomial pode ser usada para dividir um polinômio por qualquer polinômio com grau igual ou menor.
O algoritmo de divisão nos diz que um dividendo polinomial pode ser escrito como o produto do divisor e o quociente adicionado ao restante.
A divisão sintética é um atalho que pode ser usado para dividir um polinômio por um binômio na forma$x−k.$
A divisão polinomial pode ser usada para resolver problemas de aplicação, incluindo área e volume.

Notas de pé

$^1$Serviço Nacional de Parques. “Estatísticas do Lincoln Memorial Building”. www.nps.gov/linc/historycultu... statistics.htm. Acessado em 03/4/2014

Glossário

algoritmo de divisão

dado um dividendo polinomial$f(x)$ e um divisor polinomial diferente de zero$d(x)$ onde o grau de$d(x)$ é menor ou igual ao grau de$f(x)$, existem polinômios únicos$q(x)$ e$r(x)$ tais que$f(x)=d(x)q(x)+r(x)$ onde$q(x)$ é o quociente e$r(x)$ é o restante. O restante é igual a zero ou tem um grau estritamente menor que$d(x)$.

divisão sintética

um método de atalho que pode ser usado para dividir um polinômio por um binômio da forma$x−k$