3.1: Números complexos

Last updated
Save as PDF

Page ID: 189208

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Expresse raízes quadradas de números negativos como múltiplos de$i$.
Faça um gráfico de números complexos no plano complexo.
Adicione e subtraia números complexos.
Multiplique e divida números complexos.

O estudo da matemática se baseia continuamente em si mesmo. Os números inteiros negativos, por exemplo, preenchem um vazio deixado pelo conjunto de números inteiros positivos. O conjunto de números racionais, por sua vez, preenche um vazio deixado pelo conjunto de números inteiros. O conjunto de números reais preenche um vazio deixado pelo conjunto de números racionais. Não é de surpreender que o conjunto de números reais também tenha vazios. Por exemplo, ainda não temos solução para equações como

\[x^2+4=0\]

Nossas melhores suposições podem ser +2 ou —2. Mas se testarmos +2 nessa equação, isso não funcionará. Se testarmos —2, isso não funcionará. Se quisermos ter uma solução para essa equação, teremos que ir mais longe do que temos até agora. Afinal, até agora descrevemos a raiz quadrada de um número negativo como indefinida. Felizmente, existe outro sistema de números que fornece soluções para problemas como esses. Nesta seção, exploraremos esse sistema numérico e como trabalhar nele.

Expressando raízes quadradas de números negativos como múltiplos de i

Sabemos como encontrar a raiz quadrada de qualquer número real positivo. De forma semelhante, podemos encontrar a raiz quadrada de um número negativo. A diferença é que a raiz não é real. Se o valor no radicando for negativo, diz-se que a raiz é um número imaginário. O número imaginário i é definido como a raiz quadrada de menos 1.

\[\sqrt{-1}=i\]

Então, usando propriedades dos radicais,

\[i^2=(\sqrt{-1})^2=−1\]

Podemos escrever a raiz quadrada de qualquer número negativo como múltiplo de i. Considere a raiz quadrada de —25.

\[\begin{align} \sqrt{-25}&=\sqrt{25 {\cdot} (-1)}\\ &=\sqrt{25}\sqrt{-1} \\ &= 5i \end{align}\]

Usamos 5 i e não −5 i porque a raiz principal de 25 é a raiz positiva.

Um número complexo é a soma de um número real e um número imaginário. Um número complexo é expresso na forma padrão quando escrito$a+bi$ onde$a$ está a parte real e$bi$ é a parte imaginária. Por exemplo,$5+2i$ é um número complexo. Então, também é$3+4\sqrt{3}i$.

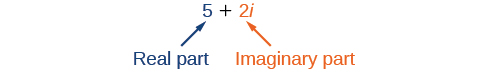
Mostrando as partes reais e imaginárias de 5 + 2i. Nesse número complexo, 5 é a parte real e 2i é a parte complexa. — Figura$\PageIndex{1}$

Os números imaginários são diferenciados dos números reais porque um número imaginário quadrado produz um número real negativo. Lembre-se, quando um número real positivo é quadrado, o resultado é um número real positivo e quando um número real negativo é quadrado, novamente, o resultado é um número real positivo. Números complexos são uma combinação de números reais e imaginários.

Números imaginários e complexos

Um número complexo é um número do formulário$a+bi$ em que

$a$é a parte real do número complexo.
$bi$é a parte imaginária do número complexo.

Se$b=0$, então$a+bi$ é um número real. Se$a=0$ e não$b$ for igual a 0, o número complexo é chamado de número imaginário. Um número imaginário é a raiz par de um número negativo.

Formulário padrão

Dado um número imaginário, expresse-o na forma padrão.

Escreva$\sqrt{−a}$ como$\sqrt{a}\sqrt{−1}$.
$\sqrt{−1}$Expresse como $i$.
Escreva$\sqrt{a}{\cdot}i$ na forma mais simples.

Exemplo$\PageIndex{1}$: Expressing an Imaginary Number in Standard Form

$\sqrt{−9}$Expresse em formato padrão.

Solução

\[\sqrt{−9}=\sqrt{9}\sqrt{−1}=3i \nonumber\]

Na forma padrão, isso é$0+3i$.

Exercício$\PageIndex{1}$

$\sqrt{−24}$Expresse em formato padrão.

Resposta: $\sqrt{−24}=0+2i\sqrt{6}$

Traçando um número complexo no plano complexo

Não podemos traçar números complexos em uma reta numérica como podemos fazer com números reais. No entanto, ainda podemos representá-los graficamente. Para representar um número complexo, precisamos abordar os dois componentes do número. Usamos o plano complexo, que é um sistema de coordenadas no qual o eixo horizontal representa o componente real e o eixo vertical representa o componente imaginário. Números complexos são os pontos no plano, expressos como pares ordenados$(a,b)$, onde$a$ representa a coordenada para o eixo horizontal e$b$ representa a coordenada para o eixo vertical.

Vamos considerar o número$−2+3i$. A parte real do número complexo é−2 e a parte imaginária é$3i$. Traçamos o par ordenado$(−2,3)$ para representar o número complexo$−2+3i$, conforme mostrado na Figura$\PageIndex{2}$

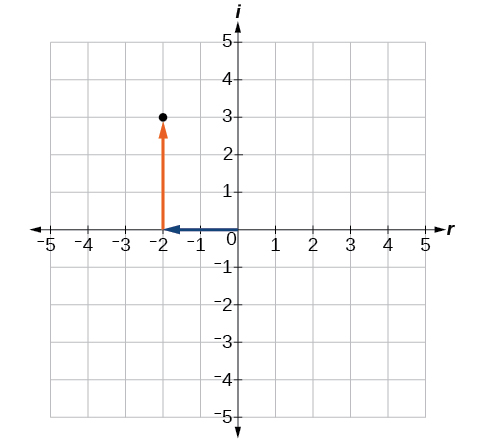
Gráfico de um número complexo, -2 + 3i. Observe que a parte real (-2) é plotada no eixo x e a parte imaginária (3i) é plotada no eixo y. — Figura$\PageIndex{2}$: Gráfico de um número complexo,$-2 + 3i$. Observe que a parte real$(-2)$ é plotada no eixo x e a parte imaginária$(3i)$ é plotada no eixo y.

Plano complexo

No plano complexo, o eixo horizontal é o eixo real e o eixo vertical é o eixo imaginário, conforme mostrado na Figura$\PageIndex{3}$.

Como...

Dado um número complexo, represente seus componentes no plano complexo.

Determine a parte real e a parte imaginária do número complexo.
Mova-se ao longo do eixo horizontal para mostrar a parte real do número.
Mova-se paralelamente ao eixo vertical para mostrar a parte imaginária do número.
Faça um gráfico do ponto.

Exemplo$\PageIndex{2}$: Plotting a Complex Number on the Complex Plane

Faça um gráfico do número complexo$3−4i$ no plano complexo.

Solução

A parte real do número complexo é 3, e a parte imaginária é$−4i$. Traçamos o par ordenado$(3,−4)$ conforme mostrado na Figura$\PageIndex{4}$.

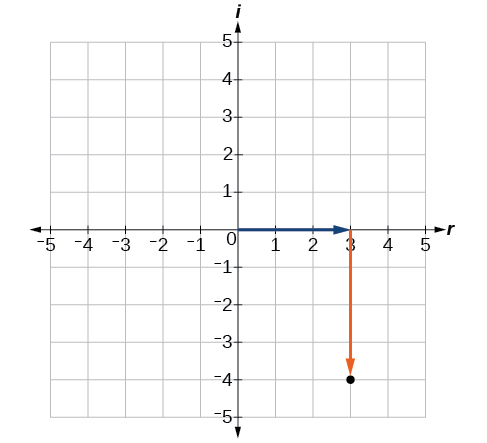
Gráfico de um número complexo, 3 - 4i. Observe que a parte real (3) é plotada no eixo x e a parte imaginária (-4i) é plotada no eixo y. — Figura$\PageIndex{4}$: Gráfico de um número complexo,$3 - 4i$. Observe que a parte real$(3)$ é plotada no eixo x e a parte imaginária$(-4i)$ é plotada no eixo y.

Exercício$\PageIndex{1}$

Faça um gráfico do número complexo$−4−i$ no plano complexo.

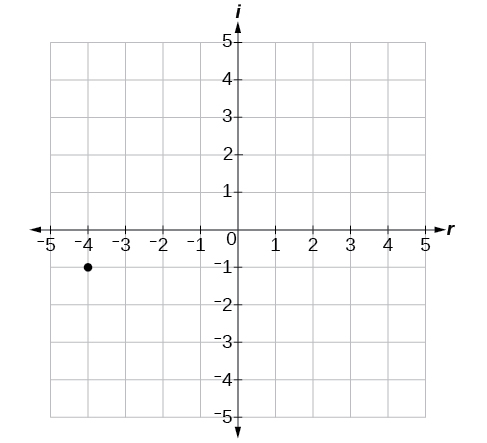
Resposta: $Gráfico do ponto representado graficamente, -4-i.$
Figura$\PageIndex{5}$

Adicionando e subtraindo números complexos

Assim como com números reais, podemos realizar operações aritméticas em números complexos. Para somar ou subtrair números complexos, combinamos as partes reais e combinamos as partes imaginárias.

Números complexos: adição e subtração

Adicionando números complexos:

\[(a+bi)+(c+di)=(a+c)+(b+d)i\]

Subtração de números complexos:

\[(a+bi)−(c+di)=(a−c)+(b−d)i\]

Como...

Dados dois números complexos, encontre a soma ou a diferença.

Identifique as partes reais e imaginárias de cada número.
Adicione ou subtraia as partes reais.
Adicione ou subtraia as partes imaginárias.

Exemplo$\PageIndex{3}$: Adding Complex Numbers

Adicione$3−4i$$2+5i$ e.

Solução

Nós adicionamos as partes reais e adicionamos as partes imaginárias.

\[\begin{align*} (a+bi)+(c+di)&=(a+c)+(b+d)i \\ (3−4i)+(2+5i)&=(3+2)+(−4+5)i \\ &=5+i \end{align*}\]

Exercício$\PageIndex{3}$

Subtraia$2+5i$ de$3–4i$.

Resposta: $(3−4i)−(2+5i)=1−9i$

Multiplicação de números complexos

Multiplicar números complexos é muito parecido com multiplicar binômios. A principal diferença é que trabalhamos com as partes real e imaginária separadamente.

Multiplicação de números complexos por um número real

Vamos começar multiplicando um número complexo por um número real. Distribuímos o número real da mesma forma que faríamos com um binômio. Então, por exemplo,

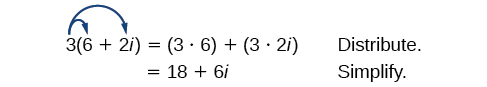
Como...

Dado um número complexo e um número real, multiplique para encontrar o produto.

Use a propriedade distributiva.
Simplifique.

Exemplo$\PageIndex{4}$: Multiplying a Complex Number by a Real Number

Encontre o produto$4(2+5i).$

Solução

Distribua o 4.

\[\begin{align*} 4(2+5i)&=(4⋅2)+(4⋅5i) \\ &=8+20i \end{align*}\]

Exercício$\PageIndex{4}$

Encontre o produto$−4(2+6i)$.

Resposta: $−8−24i$

Multiplicação de números complexos

Agora, vamos multiplicar dois números complexos. Podemos usar a propriedade distributiva ou o método FOIL. Lembre-se de que FOIL é um acrônimo para multiplicar os termos Primeiro, Externo, Interno e Último. Usando a propriedade distributiva ou o método FOIL, obtemos

\[(a+bi)(c+di)=ac+adi+bci+bdi^2 \nonumber\]

Porque$i^2=−1$, nós temos

\[(a+bi)(c+di)=ac+adi+bci−bd \nonumber\]

Para simplificar, combinamos as partes reais e combinamos as partes imaginárias.

\[(a+bi)(c+di)=(ac−bd)+(ad+bc)i \nonumber\]

Como...

Dados dois números complexos, multiplique para encontrar o produto.

Use a propriedade distributiva ou o método FOIL.
Simplifique.

Exemplo$\PageIndex{5}$: Multiplying a Complex Number by a Complex Number

Multiplique$(4+3i)(2−5i)$.

Solução

Use$(a+bi)(c+di)=(ac−bd)+(ad+bc)i$

\[\begin{align*} (4+3i)(2−5i)&=(4⋅2−3⋅(−5))+(4⋅(−5)+3⋅2)i \\ &=(8+15)+(−20+6)i \\ &=23−14i \end{align*}\]

Exercício$\PageIndex{5}$

Multiplique$(3−4i)(2+3i)$.

Resposta: $18+i$

Dividindo números complexos

A divisão de dois números complexos é mais complicada do que adição, subtração e multiplicação porque não podemos dividir por um número imaginário, o que significa que qualquer fração deve ter um denominador de número real. Precisamos encontrar um termo pelo qual possamos multiplicar o numerador e o denominador que eliminará a porção imaginária do denominador para que acabemos com um número real como denominador. Esse termo é chamado de conjugado complexo do denominador, que é encontrado alterando o sinal da parte imaginária do número complexo. Em outras palavras, o complexo conjugado de$a+bi$ é$a−bi$.

Observe que os conjugados complexos têm uma relação recíproca: o conjugado complexo de$a+bi$ é$a−bi$ e o conjugado complexo de$a−bi$ é$a+bi$. Além disso, quando uma equação quadrática com coeficientes reais tem soluções complexas, as soluções são sempre conjugadas complexas umas das outras.

Suponha que queiramos dividir$c+di$ por$a+bi$, onde nem a nem$b$ é igual a zero. Primeiro escrevemos a divisão como uma fração, depois encontramos o conjugado complexo do denominador e multiplicamos.

\[\dfrac{c+di}{a+bi} \, \text{ where $a{\neq}0$ and $b{\neq}0$} \nonumber\]

Multiplique o numerador e o denominador pelo conjugado complexo do denominador.

\[\dfrac{(c+di)}{(a+bi)}{\cdot}\dfrac{(a−bi)}{(a−bi)}=\dfrac{(c+di)(a−bi)}{(a+bi)(a−bi)} \nonumber\]

Aplique a propriedade distributiva.

\[=\dfrac{ca−cbi+adi−bdi^2}{a^2−abi+abi−b^2i^2} \nonumber\]

Simplifique, lembrando disso$i^2=−1$.

\[=\dfrac{ca−cbi+adi−bd(−1)}{a^2−abi+abi−b^2(−1)} \\ =\dfrac{(ca+bd)+(ad−cb)i}{a^2+b^2} \nonumber\]

Definição: O conjugado complexo

O conjugado complexo de um número complexo$a+bi$ é$a−bi$. É encontrado alterando o sinal da parte imaginária do número complexo. A parte real do número permanece inalterada.

Quando um número complexo é multiplicado por seu conjugado complexo, o resultado é um número real.
Quando um número complexo é adicionado ao seu conjugado complexo, o resultado é um número real.

Exemplo$\PageIndex{6}$: Finding Complex Conjugates

Encontre o conjugado complexo de cada número.

$2+i\sqrt{5}$
$−\frac{1}{2}i$

Solução

a. O número já está no formulário$a+bi$. O conjugado complexo é$a−bi$, ou$2−i\sqrt{5}$.
b. Podemos reescrever esse número no formulário$a+bi$ como$0−\frac{1}{2}i$. O conjugado complexo é$a−bi$, ou$0+\frac{1}{2}i$. Isso pode ser escrito simplesmente como$\frac{1}{2}i$.

Análise

Embora tenhamos visto que podemos encontrar o conjugado complexo de um número imaginário, na prática geralmente encontramos os conjugados complexos apenas de números complexos com um componente real e um componente imaginário. Para obter um número real de um número imaginário, podemos simplesmente multiplicar por$i$.

Como...

Dados dois números complexos, divida um pelo outro.

Escreva o problema da divisão como uma fração.
Determine o conjugado complexo do denominador.
Multiplique o numerador e o denominador da fração pelo conjugado complexo do denominador.
Simplifique.

Exemplo$\PageIndex{7}$: Dividing Complex Numbers

Divida$(2+5i)$ por$(4−i)$.

Solução

Começamos escrevendo o problema como uma fração.

\[\dfrac{(2+5i)}{(4−i)} \nonumber\]

Em seguida, multiplicamos o numerador e o denominador pelo conjugado complexo do denominador.

\[\dfrac{(2+5i)}{(4−i)}{\cdot}\dfrac{(4+i)}{(4+i)} \nonumber\]

Para multiplicar dois números complexos, expandimos o produto da mesma forma que faríamos com os polinômios (o processo comumente chamado FOIL).

\[\begin{align} \dfrac{(2+5i)}{(4−i)}{\cdot}\dfrac{(4+i)}{(4+i)}&=\dfrac{8+2i+20i+5i^2}{16+4i−4i−i^2} \\ &=\dfrac{8+2i+20i+5(−1)}{16+4i−4i−(−1)} &\text{ because $i^2=-1$} \\ &=\dfrac{3+22i}{17} \\ &=\dfrac{3}{17}+\dfrac{22}{17}i & \text{Separate real and imaginary parts.} \end{align}\]

Observe que isso expressa o quociente na forma padrão.

Exemplo$\PageIndex{8}$: Substituting a Complex Number into a Polynomial Function

Deixe$f(x)=x^2−5x+2$. Avalie$f(3+i)$.

Solução

$x=3+i$Substitua a função$f(x)=x^2−5x+2$ e simplifique.

\[\begin{align*} f(3+i) &= (3+i)^2 - 5(3+i) + 2\; \qquad \text{Substitute 3+i for x}\\ &= (3+6i+i^2) - (15+5i) + 2\; \qquad \text{Multiply}\\ &= 9+6i+(-1)-15-5i+2\; \qquad \text{Subsitute -1 for }i^2\\ &= -5+i\; \qquad \text{Combine like terms} \end{align*}\]

Análise

Nós escrevemos$f(3+i)=−5+i$. Observe que a entrada é$3+i$ e a saída é$−5+i$.

Exercício$\PageIndex{8}$

Deixe$f(x)=2x^2−3x$. Avalie$f(8−i)$.

Resposta: $102−29i$

Exemplo$\PageIndex{9}$: Substituting an Imaginary Number in a Rational Function

Deixe$f(x)=\frac{2+x}{x+3}$. Avalie$f(10i)$.

Solução

Substitua$x=10i$ e simplifique.

\[\begin{align*} &\dfrac{2+10i}{10i+3} &\text{Substitute $10i$ for $x$.} \\ &\dfrac{2+10i}{3+10i} &\text{Rewrite the denominator in standard form.} \\ &\dfrac{2+10i}{3+10i}{\cdot}\dfrac{3–10i}{3–10i} &\text{Multiply the numerator and denominator by the complex conjugate of the denominator.}\\ &\dfrac{6–20i+30i–100i^2}{9–30i+30i–100i^2} &\text{Multiply using the distributive property or the FOIL method.} \\ &\dfrac{6–20i+30i–100(–1)}{9–30i+30i–100(–1)} &\text{Substitute –1 for $i^2$.}\\ &\dfrac{106+10i}{109} &\text{Simplify.}\\ &\dfrac{106}{109}+\dfrac{10}{109} &\text{Separate the real and imaginary parts.} \end{align*}\]

Exercício$\PageIndex{9}$

Deixe$f(x)=\frac{x+1}{x−4}$. Avalie$f(−i)$.

Resposta: $−\frac{3}{17}+\frac{5i}{17}$

Simplificando os poderes do$i$

Os poderes do$i$ são cíclicos. Vamos ver o que acontece quando o elevamos a poderes crescentes.

\[\begin{align*} i^1&=i \\[4pt] i^2&=−1 \\[4pt] i^3&=i^2⋅i=−1⋅i=−i \\[4pt] i^4&=i^3⋅i=−i⋅i=−i^2=−(−1)=1 \\[4pt] i^5&=i^4⋅i=1⋅i=i \end{align*}\]

Podemos ver que quando chegamos à quinta potência de$i$, ela é igual à primeira potência. À medida que continuamos a nos multiplicar$i$ por si só para aumentar os poderes, veremos um ciclo de 4. Vamos examinar os próximos 4 poderes do$i$.

\[\begin{align*} i^6&=i^5⋅i=i⋅i=i^2=−1 \\[4pt] i^7&=i^6⋅i=i^2⋅i=i^3=−i \\[4pt] i^8&=i^7⋅i=i^3⋅i=i^4=1 \\[4pt] i^9&=i^8⋅i=i^4⋅i=i^5=i \end{align*}\]

Exemplo$\PageIndex{10}$: Simplifying Powers of $i$

Avalie$i^{35}$.

Solução

Desde então$i^4=1$, podemos simplificar o problema considerando o maior número possível de fatores de i^4. Para fazer isso, primeiro determine quantas vezes 4 entra em 35:$35=4⋅8+3$.

\[i^{35}=i^{4⋅8+3}=i^{4⋅8}⋅i^{3}=(i^4)^8⋅i^3=1^8⋅i^3=i^3=−i \nonumber \]

PERGUNTAS E RESPOSTAS

Podemos escrever$i^35$ de outras formas úteis?

Como vimos no Exemplo$\PageIndex{10}$, reduzimos$i^{35}$ para$i^3$ dividindo o expoente por 4 e usando o restante para encontrar a forma simplificada. Mas talvez outra fatoração de$i^{35}$ possa ser mais útil. A tabela$\PageIndex{1}$ mostra algumas outras fatorizações possíveis.

Tabela$\PageIndex{1}$: Cada uma delas acabará resultando na resposta que obtivemos acima, mas pode exigir várias etapas a mais do que nosso método anterior.
Fatoração de$i^{35}$	$i^{34}{\cdot}i$	$i^{33}{\cdot}i^2$	$i^{31}{\cdot}i^4$	$i^{19}{\cdot}i^{16}$
Forma reduzida	$\big(i^2\big)^{17}{\cdot}i$	$i^{33}{\cdot}(-1)$	$i^{31}{\cdot}1$	$i^{19}{\cdot}\big(i^4\big)^4$
Formulário simplificado	$(-1)^{17}{\cdot}i$	$-i^{33}$	$i^{31}$	$i^{19}$

Conceitos-chave

A raiz quadrada de qualquer número negativo pode ser escrita como múltiplo de$i$.
Para traçar um número complexo, usamos duas linhas numéricas, cruzadas para formar o plano complexo. O eixo horizontal é o eixo real e o eixo vertical é o eixo imaginário.
Números complexos podem ser somados e subtraídos combinando as partes reais e combinando as partes imaginárias.
Números complexos podem ser multiplicados e divididos.
Para multiplicar números complexos, distribua da mesma forma que ocorre com os polinômios.
Para dividir números complexos, multiplique o numerador e o denominador pelo conjugado complexo do denominador para eliminar o número complexo do denominador.
Os poderes do$i$ são cíclicos, repetindo-se a cada quatro.

Glossário

complexo conjuga
o número complexo no qual o sinal da parte imaginária é alterado e a parte real do número permanece inalterada; quando adicionado ou multiplicado pelo número complexo original, o resultado é um número real

número complexo
a soma de um número real e um número imaginário, escrito na forma padrão$a+bi$, onde$a$ está a parte real e$bi$ é a parte imaginária

plano complexo -
um sistema de coordenadas no qual o eixo horizontal é usado para representar a parte real de um número complexo e o eixo vertical é usado para representar a parte imaginária de um número complexo.

número imaginário
um número na forma bi onde$i=\sqrt{−1}$

Fatoração de\(i^{35}\)	\(i^{34}{\cdot}i\)	\(i^{33}{\cdot}i^2\)	\(i^{31}{\cdot}i^4\)	\(i^{19}{\cdot}i^{16}\)
Forma reduzida	\(\big(i^2\big)^{17}{\cdot}i\)	\(i^{33}{\cdot}(-1)\)	\(i^{31}{\cdot}1\)	\(i^{19}{\cdot}\big(i^4\big)^4\)
Formulário simplificado	\((-1)^{17}{\cdot}i\)	\(-i^{33}\)	\(i^{31}\)	\(i^{19}\)

Expressando raízes quadradas de números negativos como múltiplos de i

Traçando um número complexo no plano complexo

Adicionando e subtraindo números complexos

Multiplicação de números complexos

Multiplicação de números complexos por um número real

Multiplicação de números complexos

Dividindo números complexos

Simplificando os poderes do\(i\)

Conceitos-chave

Glossário