1.1: Funções e notação de funções
- Page ID
- 189192
Objetivos de
- Determine se uma relação representa uma função.
- Encontre o valor de uma função.
- Determine se uma função é individual.
- Use o teste de linha vertical para identificar funções.
- Faça um gráfico das funções listadas na biblioteca de funções.
Um avião a jato muda de altitude à medida que sua distância do ponto de partida de um voo aumenta. O peso de uma criança em crescimento aumenta com o tempo. Em cada caso, uma quantidade depende da outra. Há uma relação entre as duas quantidades que podemos descrever, analisar e usar para fazer previsões. Nesta seção, analisaremos essas relações.
Determinando se uma relação representa uma função
Uma relação é um conjunto de pares ordenados. O conjunto dos primeiros componentes de cada par ordenado é chamado de domínio e o conjunto dos segundos componentes de cada par ordenado é chamado de intervalo. Considere o seguinte conjunto de pares ordenados. Os primeiros números em cada par são os primeiros cinco números naturais. O segundo número em cada par é o dobro do primeiro.
\[\{(1, 2), (2, 4), (3, 6), (4, 8), (5, 10)\}\tag{1.1.1}\]
O domínio é\(\{1, 2, 3, 4, 5\}\). O alcance é\(\{2, 4, 6, 8, 10\}\).
Observe que cada valor no domínio também é conhecido como valor de entrada ou variável independente e geralmente é rotulado com a letra minúscula\(x\). Cada valor no intervalo também é conhecido como valor de saída, ou variável dependente, e geralmente é rotulado como letra minúscula\(y\).
Uma função\(f\) é uma relação que atribui um único valor no intervalo a cada valor no domínio. Em outras palavras, nenhum\(x\) valor é repetido. Para nosso exemplo, que relaciona os primeiros cinco números naturais com números que dobram seus valores, essa relação é uma função porque cada elemento no domínio, {1, 2, 3, 4, 5}, está emparelhado com exatamente um elemento no intervalo,\(\{2, 4, 6, 8, 10\}\).
Agora, vamos considerar o conjunto de pares ordenados que relaciona os termos “par” e “ímpar” aos primeiros cinco números naturais. Pareceria como
\[\mathrm{\{(odd, 1), (even, 2), (odd, 3), (even, 4), (odd, 5)\}} \tag{1.1.2}\]
Observe que cada elemento no domínio, {par, ímpar} não está emparelhado com exatamente um elemento no intervalo,\(\{1, 2, 3, 4, 5\}\). Por exemplo, o termo “ímpar” corresponde a três valores do intervalo\(\{1, 3, 5\},\) e o termo “par” corresponde a dois valores do intervalo,\(\{2, 4\}\). Isso viola a definição de uma função, então essa relação não é uma função.
A figura\(\PageIndex{1}\) compara relações que são funções e não funções.
![[Três relações que demonstram o que constitui uma função.]](https://math.libretexts.org/@api/deki/files/861/CNX_Precalc_Figure_01_01_001.jpg)
Função
Uma função é uma relação na qual cada valor de entrada possível leva a exatamente um valor de saída. Dizemos que “a saída é uma função da entrada”.
Os valores de entrada compõem o domínio e os valores de saída compõem o intervalo.
Como fazer: Dada uma relação entre duas quantidades, determine se a relação é uma função
- Identifique os valores de entrada.
- Identifique os valores de saída.
- Se cada valor de entrada levar a apenas um valor de saída, classifique a relação como uma função. Se algum valor de entrada levar a duas ou mais saídas, não classifique a relação como uma função.
Exemplo\(\PageIndex{1}\): Determining If Menu Price Lists Are Functions
O menu da cafeteria, mostrado na Figura,\(\PageIndex{2}\) consiste em itens e seus preços.
- O preço é uma função do item?
- O item é uma função do preço?

Solução
- Vamos começar considerando a entrada como os itens no menu. Os valores de saída são então os preços. Veja a Figura\(\PageIndex{3}\).
![[Um menu de preços de donuts em uma cafeteria onde um donut simples custa $1,49 e um donut de geleia e um donut de chocolate custam $1,99.]](https://math.libretexts.org/@api/deki/files/865/CNX_Precalc_Figure_01_01_027.v2.jpg)
Cada item no menu tem apenas um preço, então o preço é uma função do item.
- Dois itens do menu têm o mesmo preço. Se considerarmos os preços como os valores de entrada e os itens como a saída, o mesmo valor de entrada poderá ter mais de uma saída associada a ele. Veja a Figura\(\PageIndex{4}\).
![[Associação dos preços aos donuts.]](https://math.libretexts.org/@api/deki/files/866/CNX_Precalc_Figure_01_01_028.jpg)
Portanto, o item não é uma função do preço.
Exemplo\(\PageIndex{2}\): Determining If Class Grade Rules Are Functions
Em uma aula de matemática específica, a nota percentual geral corresponde a uma média de notas. A média de notas é uma função da nota percentual? A nota percentual é uma função da média de notas? A tabela\(\PageIndex{1}\) mostra uma possível regra para atribuir pontos de nota.
| Grau percentual | 0—56 | 57—61 | 62—66 | 67—71 | 72—77 | 78—86 | 87—91 | 92—100 |
| Média de notas | 0,0 | 1,0 | 1,5 | 2.0 | 2,5 | 3,0 | 3.5 | 4,0 |
Solução
Para qualquer nota percentual obtida, há uma média de notas associada, portanto, a média de notas é uma função da nota percentual. Em outras palavras, se inserirmos a nota percentual, a saída será uma média de notas específica.
No sistema de avaliação fornecido, há uma faixa de notas percentuais que correspondem à mesma média de notas. Por exemplo, estudantes que recebem uma média de 3,0 pontos percentuais podem ter uma variedade de notas percentuais que variam de 78 até 86. Portanto, a nota percentual não é uma função da média de notas.
Exercício\(\PageIndex{2}\)
A tabela\(\PageIndex{2}\) lista os cinco maiores jogadores de beisebol de todos os tempos em ordem de classificação.
| Jogador | Classificação |
|---|---|
| Querida Ruth | 1 |
| Willie Mays | 2 |
| Ty Cobb | 3 |
| Walter Johnson | 4 |
| Hank Aaron | 5 |
- A classificação é uma função do nome do jogador?
- O nome do jogador é uma função da classificação?
- Responda a
-
sim
- Resposta b
-
sim. (Nota: Se dois jogadores tivessem empatado, digamos, no 4º lugar, o nome não teria sido uma função da classificação.)
Usando a notação de função
Depois de determinarmos que um relacionamento é uma função, precisamos exibir e definir os relacionamentos funcionais para que possamos entendê-los e usá-los e, às vezes, também para que possamos programá-los em computadores. Existem várias formas de representar funções. Uma notação de função padrão é uma representação que facilita o trabalho com funções.
Para representar “a altura é uma função da idade”, começamos identificando as variáveis\(h\) descritivas da altura e\(a\) da idade. As letras\(f\),\(g\), e\(h\) são frequentemente usadas para representar funções da mesma forma que usamos\(x\),\(y\), e\(z\) para representar números e\(A\),\(B\), e\(C\) para representar conjuntos.
\[\begin{array}{ll} h \text{ is } f \text{ of }a \;\;\;\;\;\; & \text{We name the function }f \text{; height is a function of age.} \\ h=f(a) & \text{We use parentheses to indicate the function input.} \\ f(a) & \text{We name the function }f \text{ ; the expression is read as “ }f \text{ of }a \text{.”}\end{array}\]
Lembre-se de que podemos usar qualquer letra para nomear a função; a notação nos\(h(a)\) mostra que isso\(h\) depende de\(a\). O valor\(a\) deve ser colocado na função\(h\) para obter um resultado. Os parênteses indicam que a idade é inserida na função; eles não indicam multiplicação.
Também podemos dar uma expressão algébrica como entrada para uma função. Por exemplo,\(f(a+b)\) significa “primeiro adicione\(a\) e\(b\), e o resultado é a entrada para a função”\(f\). As operações devem ser executadas nessa ordem para obter o resultado correto.
Notação de função
A notação\(y=f(x)\) define uma função chamada\(f\). Isso é lido como “\(y\)é uma função de”\(x\). A letra\(x\) representa o valor de entrada, ou variável independente. A letra\(y\), ou\(f(x)\), representa o valor de saída ou a variável dependente.
Exemplo\(\PageIndex{3}\): Using Function Notation for Days in a Month
Use a notação de função para representar uma função cuja entrada é o nome de um mês e a saída é o número de dias nesse mês.
Solução
Usando a notação de função para dias em um mês
Use a notação de função para representar uma função cuja entrada é o nome de um mês e a saída é o número de dias nesse mês.
O número de dias em um mês é uma função do nome do mês, então, se nomearmos a função\(f\), escreveremos\(\text{days}=f(\text{month})\) ou\(d=f(m)\). O nome do mês é a entrada para uma “regra” que associa um número específico (a saída) a cada entrada.
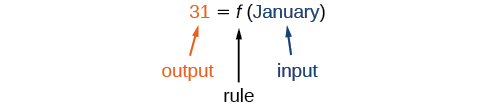
Por exemplo\(f(\text{March})=31\), porque março tem 31 dias. A notação nos\(d=f(m)\) lembra que o número de dias\(d\) (a saída) depende do nome do mês\(m\) (a entrada).
Análise
Observe que as entradas para uma função não precisam ser números; as entradas da função podem ser nomes de pessoas, rótulos de objetos geométricos ou qualquer outro elemento que determine algum tipo de saída. No entanto, a maioria das funções com as quais trabalharemos neste livro terão números como entradas e saídas.
Exemplo\(\PageIndex{3B}\): Interpreting Function Notation
Uma função\(N=f(y)\) fornece o número de policiais,\(N\), em uma cidade em um ano\(y\). O que\(f(2005)=300\) representa?
Solução
Quando lemos\(f(2005)=300\), vemos que o ano de entrada é 2005. O valor da produção, o número de policiais\((N)\), é 300. Lembre-se,\(N=f(y)\). A declaração nos\(f(2005)=300\) diz que no ano de 2005 havia 300 policiais na cidade.
Exercício\(\PageIndex{3}\)
Use a notação funcional para expressar o peso de um porco em libras em função de sua idade em dias\(d\).
- Resposta
-
\(w=f(d)\)
PERGUNTAS E RESPOSTAS
Em vez de uma notação como\(y=f(x)\), poderíamos usar o mesmo símbolo para a saída e para a função, como, por exemplo\(y=y(x)\), significando “\(y\)é uma função de\(x\)?”
Sim, isso geralmente é feito, especialmente em disciplinas aplicadas que usam matemática superior, como física e engenharia. No entanto, ao explorar a matemática em si, gostamos de manter uma distinção entre uma função como\(f\), que é uma regra ou procedimento, e a saída y que obtemos aplicando\(f\) a uma entrada específica\(x\). É por isso que geralmente usamos notação como\(y=f(x),P=W(d)\), e assim por diante.
Representando funções usando tabelas
Um método comum de representação de funções é na forma de uma tabela. As linhas ou colunas da tabela exibem os valores de entrada e saída correspondentes. Em alguns casos, esses valores representam tudo o que sabemos sobre o relacionamento; outras vezes, a tabela fornece alguns exemplos selecionados de um relacionamento mais completo.
A tabela\(\PageIndex{3}\) lista o número de entrada de cada mês (\(\text{January}=1\)\(\text{February}=2\), e assim por diante) e o valor de saída do número de dias nesse mês. Essas informações representam tudo o que sabemos sobre os meses e dias de um determinado ano (isso não é um ano bissexto). Observe que, nesta tabela, definimos uma função de dias em um mês em\(f\) que\(D=f(m)\) identifica meses por um número inteiro em vez de pelo nome.
| Número do mês,\(m\) (entrada) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Dias no mês,\(D\) (saída) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
A tabela\(\PageIndex{4}\) define uma função\(Q=g(n)\) Lembre-se, essa notação nos diz que\(g\) é o nome da função que recebe a entrada\(n\) e fornece a saída\(Q\).
| \(n\) | 1 | 2 | 3 | 4 | 5 |
| \(Q\) | 8 | 6 | 7 | 6 | 8 |
A tabela\(\PageIndex{5}\) mostra a idade das crianças em anos e suas alturas correspondentes. Esta tabela exibe apenas alguns dos dados disponíveis para as alturas e idades das crianças. Podemos ver imediatamente que essa tabela não representa uma função porque o mesmo valor de entrada, 5 anos, tem dois valores de saída diferentes, 40 pol. e 42 pol.
| Idade em anos,\(a\) (entrada) | 5 | 5 | 6 | 7 | 8 | 9 | 10 |
| Altura em polegadas,\(h\) (saída) | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
Como fazer: Dada uma tabela de valores de entrada e saída, determine se a tabela representa uma função
- Identifique os valores de entrada e saída.
- Verifique se cada valor de entrada está emparelhado com apenas um valor de saída. Em caso afirmativo, a tabela representa uma função.
Exemplo\(\PageIndex{5}\): Identifying Tables that Represent Functions
Qual tabela, tabela\(\PageIndex{6}\)\(\PageIndex{7}\), tabela ou tabela\(\PageIndex{8}\) representa uma função (se houver)?
| Entrada | Saída |
|---|---|
| 2 | 1 |
| 5 | 3 |
| 8 | 6 |
| Entrada | Saída |
|---|---|
| -3 | 5 |
| 0 | 1 |
| 4 | 5 |
| Entrada | Saída |
|---|---|
| 1 | 0 |
| 5 | 2 |
| 5 | 4 |
Solução
Tabela\(\PageIndex{6}\) e tabela\(\PageIndex{7}\) definem funções. Em ambos, cada valor de entrada corresponde exatamente a um valor de saída. \(\PageIndex{8}\)A tabela não define uma função porque o valor de entrada de 5 corresponde a dois valores de saída diferentes.
Quando uma tabela representa uma função, os valores de entrada e saída correspondentes também podem ser especificados usando a notação de função.
A função representada pela Tabela\(\PageIndex{6}\) pode ser representada escrevendo
\[f(2)=1\text{, }f(5)=3\text{, and }f(8)=6 \nonumber\]
Da mesma forma, as declarações
\[g(−3)=5\text{, }g(0)=1\text{, and }g(4)=5 \nonumber\]
representam a função na Tabela\(\PageIndex{7}\).
A tabela\(\PageIndex{8}\) não pode ser expressa de forma semelhante porque não representa uma função.
Exercício\(\PageIndex{5}\)
A tabela\(\PageIndex{9}\) representa uma função?
| Entrada | Saída |
|---|---|
| 1 | 10 |
| 2 | 100 |
| 3 | 1000 |
- Resposta
-
sim
Encontrando valores de entrada e saída de uma função
Quando sabemos um valor de entrada e queremos determinar o valor de saída correspondente para uma função, avaliamos a função. A avaliação sempre produzirá um resultado porque cada valor de entrada de uma função corresponde exatamente a um valor de saída.
Quando conhecemos um valor de saída e queremos determinar os valores de entrada que produziriam esse valor de saída, definimos a saída igual à fórmula da função e resolvemos a entrada. A solução pode produzir mais de uma solução porque valores de entrada diferentes podem produzir o mesmo valor de saída.
Avaliação de funções em formas algébricas
Quando temos uma função em forma de fórmula, geralmente é uma questão simples avaliar a função. Por exemplo, a função\(f(x)=5−3x^2\) pode ser avaliada ao quadrado do valor de entrada, multiplicando por 3 e, em seguida, subtraindo o produto de 5.
Como fazer: Dada a fórmula de uma função, avalie.
Dada a fórmula para uma função, avalie.
- Substitua a variável de entrada na fórmula pelo valor fornecido.
- Calcule o resultado.
Exemplo\(\PageIndex{6A}\): Evaluating Functions at Specific Values
1. Avalie\(f(x)=x^2+3x−4\) em
- \(2\)
- \(a\)
- \(a+h\)
- Avalie\(\frac{f(a+h)−f(a)}{h}\)
Solução
Substitua o x na função por cada valor especificado.
a. Como o valor de entrada é um número, 2, podemos usar álgebra simples para simplificar.
\[\begin{align*}f(2)&=2^2+3(2)−4\\&=4+6−4\\ &=6\end{align*}\]
b. Nesse caso, o valor de entrada é uma letra, então não podemos simplificar ainda mais a resposta.
\[f(a)=a^2+3a−4\nonumber\]
c. Com um valor de entrada de\(a+h\), devemos usar a propriedade distributiva.
\[\begin{align*}f(a+h)&=(a+h)^2+3(a+h)−4\\&=a^2+2ah+h^2+3a+3h−4 \end{align*}\]
d. Nesse caso, aplicamos os valores de entrada à função mais de uma vez e, em seguida, realizamos operações algébricas no resultado. Nós já descobrimos que
\[f(a+h)=a^2+2ah+h^2+3a+3h−4\nonumber\]
e sabemos que
\[f(a)=a^2+3a−4 \nonumber\]
Agora combinamos os resultados e simplificamos.
\[\begin{align*}\dfrac{f(a+h)−f(a)}{h}&=\dfrac{(a^2+2ah+h^2+3a+3h−4)−(a^2+3a−4)}{h}\\ &=\dfrac{(2ah+h^2+3h)}{h} \\ &=\dfrac{h(2a+h+3)}{h} & &\text{Factor out h.}\\ &=2a+h+3 & & \text{Simplify.}\end{align*}\]
Exemplo\(\PageIndex{6B}\): Evaluating Functions
Dada a função\(h(p)=p^2+2p\), avalie\(h(4)\).
Solução
Para avaliar\(h(4)\), substituímos o valor 4 pela variável de entrada p na função dada.
\[\begin{align*}h(p)&=p^2+2p\\h(4)&=(4)^2+2(4)\\ &=16+8\\&=24\end{align*}\]
Portanto, para uma entrada de 4, temos uma saída de 24.
Exercício\(\PageIndex{6}\)
Dada a função\(g(m)=\sqrt{m−4}\), avalie\(g(5)\).
- Resposta
-
\(g(5)=1\)
Exemplo\(\PageIndex{7}\): Solving Functions
Dada a função\(h(p)=p^2+2p\), resolva para\(h(p)=3\).
Solução
\[\begin{array}{rl} h(p)=3\\p^2+2p=3 & \text{Substitute the original function}\\ p^2+2p−3=0 & \text{Subtract 3 from each side.}\\(p+3)(p−1)=0&\text{Factor.}\end{array} \nonumber \]
Se\((p+3)(p−1)=0\), um\((p+3)=0\) ou\((p−1)=0\) (ou ambos iguais\(0\)). Definiremos cada fator como igual\(0\) e resolveremos para\(p\) em cada caso.
\[(p+3)=0,\; p=−3 \nonumber \]
\[(p−1)=0,\, p=1 \nonumber\]
Isso nos dá duas soluções. A saída\(h(p)=3\) quando a entrada é\(p=1\) ou\(p=−3\). Também podemos verificar representando graficamente, como na Figura\(\PageIndex{6}\). O gráfico verifica isso\(h(1)=h(−3)=3\)\(h(4)=24\) e.
![[Gráfico de uma parábola com pontos rotulados (-3, 3), (1, 3) e (4, 24).]](https://math.libretexts.org/@api/deki/files/868/CNX_Precalc_Figure_01_01_006.jpg)
Exercício\(\PageIndex{7}\)
Dada a função\(g(m)=\sqrt{m−4}\), resolva\(g(m)=2\).
- Resposta
-
\(m=8\)
Avaliando funções expressas em fórmulas
Algumas funções são definidas por regras ou procedimentos matemáticos expressos em forma de equação. Se for possível expressar a saída da função com uma fórmula envolvendo a quantidade de entrada, então podemos definir uma função na forma algébrica. Por exemplo, a equação\(2n+6p=12\) expressa uma relação funcional entre\(n\)\(p\) e. Podemos reescrevê-lo para decidir se\(p\) é uma função de\(n\).
Como: Dada uma função em forma de equação, escreva sua fórmula algébrica.
- Resolva a equação para isolar a variável de saída em um lado do sinal de igual, com o outro lado como uma expressão que envolve somente a variável de entrada.
- Use todos os métodos algébricos usuais para resolver equações, como adicionar ou subtrair a mesma quantidade de ou para ambos os lados, ou multiplicar ou dividir os dois lados da equação pela mesma quantidade.
Exemplo\(\PageIndex{8A}\): Finding an Equation of a Function
Expresse o relacionamento\(2n+6p=12\) como uma função\(p=f(n)\), se possível.
Solução
Para expressar o relacionamento dessa forma, precisamos ser capazes de escrever o relacionamento onde\(p\) é uma função de\(n\), o que significa escrevê-lo como\(p=[\text{expression involving }n]\).
\[\begin{align*}2n+6p&=12 \\ 6p&=12−2n && \text{Subtract 2n from both sides.} \\ p&=\dfrac{12−2n}{6} & &\text{Divide both sides by 6 and simplify.} \\ p&=\frac{12}{6}−\frac{2n}{6} \\ p&=2−\frac{1}{3}n\end{align*}\]
Portanto\(p\), em função de\(n\) é escrito como
\[p=f(n)=2−\frac{1}{3}n \nonumber\]
Análise
É importante observar que nem toda relação expressa por uma equação também pode ser expressa como uma função com uma fórmula.
Exemplo\(\PageIndex{8B}\): Expressing the Equation of a Circle as a Function
A equação\(x^2+y^2=1\) representa uma função com\(x\) entrada e\(y\) saída? Em caso afirmativo, expresse o relacionamento como uma função\(y=f(x)\).
Solução
Primeiro, subtraímos\(x^2\) dos dois lados.
\[y^2=1−x^2 \nonumber\]
Agora tentamos resolver para\(y\) nesta equação.
\[y=\pm\sqrt{1−x^2} \nonumber\]
\[\text{so, }y=\sqrt{1−x^2}\;\text{and}\;y = −\sqrt{1−x^2} \nonumber\]
Obtemos duas saídas correspondentes à mesma entrada, portanto, essa relação não pode ser representada como uma única função\(y=f(x)\).
Exercício\(\PageIndex{8}\)
Se\(x−8y^3=0\),\(y\) expresse em função de\(x\).
- Responda
-
\(y=f(x)=\dfrac{\sqrt[3]{x}}{2}\)
PERGUNTAS E RESPOSTAS
Existem relações expressas por uma equação que representa uma função, mas que ainda não pode ser representada por uma fórmula algébrica?
Sim, isso pode acontecer. Por exemplo, dada a equação\(x=y+2^y\), se quisermos expressar y como uma função de x, não existe uma fórmula algébrica simples envolvendo apenas o\(x\) que é igual\(y\). No entanto, cada um\(x\) determina um valor exclusivo para\(y\), e existem procedimentos matemáticos pelos quais\(y\) podem ser encontrados com a precisão desejada. Nesse caso, dizemos que a equação fornece uma regra implícita (implícita) para\(y\) em função de\(x\), mesmo que a fórmula não possa ser escrita explicitamente.
Avaliando uma função dada em forma tabular
Como vimos acima, podemos representar funções em tabelas. Por outro lado, podemos usar informações em tabelas para escrever funções e avaliar funções usando as tabelas. Por exemplo, até que ponto nossos animais de estimação se lembram das boas lembranças que compartilhamos com eles? Há uma lenda urbana de que um peixinho dourado tem uma memória de 3 segundos, mas isso é apenas um mito. O peixe dourado pode se lembrar de até 3 meses, enquanto o peixe beta tem uma memória de até 5 meses. E embora a memória de um filhote não seja superior a 30 segundos, o cão adulto consegue se lembrar por 5 minutos. Isso é escasso em comparação com um gato, cuja memória dura 16 horas.
A função que relaciona o tipo de animal de estimação com a duração de sua memória é mais facilmente visualizada com o uso de uma tabela (Tabela\(\PageIndex{10}\)).
| Memória do animal | período em horas |
|---|---|
| Cachorro | 0,008 |
| Cão adulto | 0,083 |
| Gato | 3 |
| Peixe dourado | 2160 |
| Peixe beta | 3600 |
Às vezes, avaliar uma função em forma de tabela pode ser mais útil do que usar equações. Aqui, vamos chamar a função\(P\). O domínio da função é o tipo de animal de estimação e o intervalo é um número real que representa o número de horas de duração da memória do animal. Podemos avaliar a função\(P\) no valor de entrada de “peixinho dourado”. Nós escreveríamos\(P(goldfish)=2160\). Observe que, para avaliar a função em forma de tabela, identificamos o valor de entrada e o valor de saída correspondente na linha pertinente da tabela. A forma tabular da função P parece ideal para essa função, mais do que escrevê-la em forma de parágrafo ou função.
Como fazer: Dada uma função representada por uma tabela, identifique valores específicos de saída e entrada
1. Encontre a entrada fornecida na linha (ou coluna) dos valores de entrada.
2. Identifique o valor de saída correspondente emparelhado com esse valor de entrada.
3. Encontre os valores de saída fornecidos na linha (ou coluna) dos valores de saída, observando toda vez que o valor de saída aparece.
4. Identifique o (s) valor (es) de entrada correspondentes ao valor de saída fornecido.
Exemplo\(\PageIndex{9}\): Evaluating and Solving a Tabular Function
Usando a tabela\(\PageIndex{11}\),
a. Avalie\(g(3)\).
b. Resolver\(g(n)=6\).
| \(n\) | 1 | 2 | 3 | 4 | 5 |
| \(g(n)\) | 8 | 6 | 7 | 6 | 8 |
Solução
a. Avaliar\(g(3)\) significa determinar o valor de saída da função\(g\) para o valor de entrada de\(n=3\). O valor de saída da tabela correspondente a\(n=3\) é 7, então\(g(3)=7\).
b. Resolver\(g(n)=6\) significa identificar os valores de entrada, n, que produzem um valor de saída de 6. A tabela\(\PageIndex{12}\) mostra duas soluções: 2 e 4.
| \(n\) | 1 | 2 | 3 | 4 | 5 |
| \(g(n)\) | 8 | 6 | 7 | 6 | 8 |
Quando inserimos 2 na função\(g\), nossa saída é 6. Quando inserimos 4 na função\(g\), nossa saída também é 6.
Exercício\(\PageIndex{1}\)
Usando a tabela\(\PageIndex{12}\), avalie\(g(1)\).
- Responda
-
\(g(1)=8\)
Encontrando valores de funções a partir de um gráfico
Avaliar uma função usando um gráfico também requer encontrar o valor de saída correspondente para um determinado valor de entrada, somente nesse caso, encontramos o valor de saída observando o gráfico. Resolver uma equação de função usando um gráfico requer encontrar todas as instâncias do valor de saída fornecido no gráfico e observar o (s) valor (es) de entrada correspondente (s).
Exemplo\(\PageIndex{10}\): Reading Function Values from a Graph
Dado o gráfico na Figura\(\PageIndex{7}\),
- Avalie\(f(2)\).
- Resolver\(f(x)=4\).
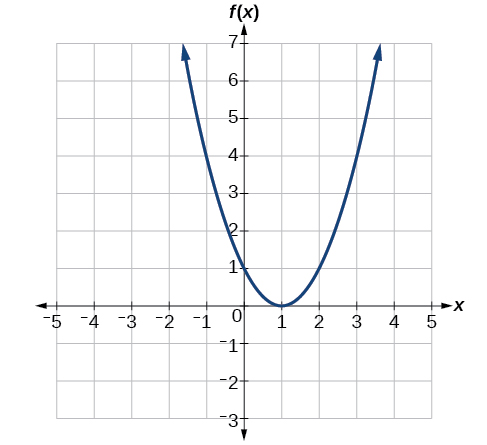
Solução
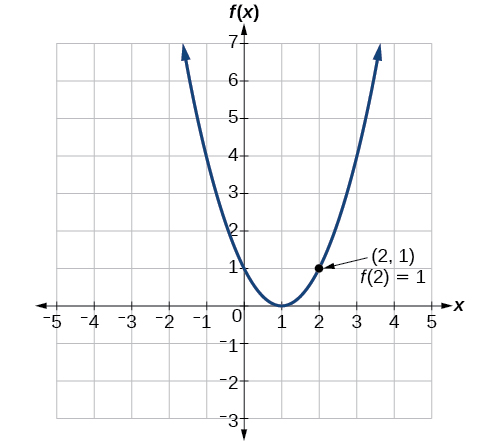
Para avaliar\(f(2)\), localize o ponto na curva onde e\(x=2\), em seguida, leia a coordenada y desse ponto. O ponto tem coordenadas\((2,1)\), então\(f(2)=1\). Veja a Figura\(\PageIndex{8}\).
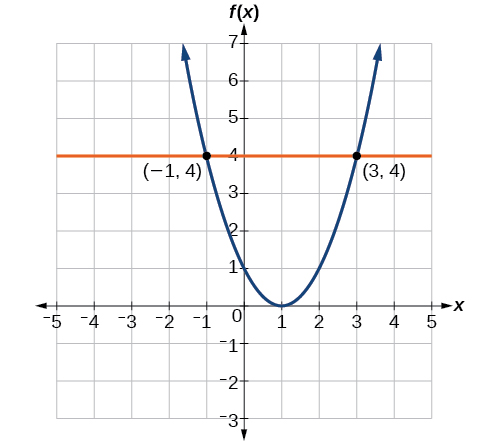
Para resolver\(f(x)=4\), encontramos o valor de saída 4 no eixo vertical. Movendo-se horizontalmente ao longo da linha\(y=4\), localizamos dois pontos da curva com valor de saída 4:\((−1,4)\)\((3,4)\) e. Esses pontos representam as duas soluções para\(f(x)=4\): −1 ou 3. Isso significa que\(f(−1)=4\) e\(f(3)=4\), ou quando a entrada é −1 ou 3, a saída é 4. Veja a Figura\(\PageIndex{9}\).
Exercício\(\PageIndex{10}\)
Dado o gráfico na Figura\(\PageIndex{7}\), resolva\(f(x)=1\).
- Responda
-
\(x=0\)ou\(x=2\)
Determinando se uma função é individual
Algumas funções têm um determinado valor de saída que corresponde a dois ou mais valores de entrada. Por exemplo, no gráfico de ações mostrado na Figura no início deste capítulo, o preço das ações era de $1000 em cinco datas diferentes, o que significa que havia cinco valores de entrada diferentes que resultaram no mesmo valor de saída de $1000.
No entanto, algumas funções têm apenas um valor de entrada para cada valor de saída, além de ter apenas uma saída para cada entrada. Chamamos essas funções de funções individuais. Como exemplo, considere uma escola que usa apenas notas de letras e equivalentes decimais, conforme listado na Tabela\(\PageIndex{13}\).
| Grau da letra | Média de notas |
|---|---|
| UMA | 4,0 |
| B | 3,0 |
| C | 2.0 |
| D | 1,0 |
Esse sistema de classificação representa uma função individual, porque cada entrada de letra produz uma saída média de notas específica e cada média de notas corresponde a uma letra de entrada.
Para visualizar esse conceito, vamos analisar novamente as duas funções simples esboçadas em Figuras\(\PageIndex{1a}\)\(\PageIndex{1b}\) e. A função na parte (a) mostra uma relação que não é uma função individual porque as entradas\(q\) e\(r\) ambas fornecem saída\(n\). A função na parte (b) mostra uma relação que é uma função individual porque cada entrada está associada a uma única saída.
Funções individuais
Uma função um-para-um é uma função na qual cada valor de saída corresponde exatamente a um valor de entrada.
Exemplo\(\PageIndex{11}\): Determining Whether a Relationship Is a One-to-One Function
A área de um círculo é função de seu raio? Se sim, a função é individual?
Solução
Um círculo de raio\(r\) tem uma área única medida dada por\(A={\pi}r^2\), portanto, para qualquer entrada\(r\), há apenas uma saída,\(A\). A área é uma função do raio\(r\).
Se a função for individual, o valor de saída, a área, deverá corresponder a um valor de entrada exclusivo, o raio. Qualquer medida de área\(A\) é dada pela fórmula\(A={\pi}r^2\). Porque áreas e raios são números positivos, existe exatamente uma solução:\(\sqrt{\frac{A}{\pi}}\). Portanto, a área de um círculo é uma função individual do raio do círculo.
Exercício\(\PageIndex{11A}\)
- O saldo é uma função do número da conta bancária?
- O número de uma conta bancária é uma função do saldo?
- O saldo é uma função individual do número da conta bancária?
- Responda
-
a. sim, porque cada conta bancária tem um único saldo a qualquer momento;
b. não, porque vários números de contas bancárias podem ter o mesmo saldo;
c. não, porque a mesma saída pode corresponder a mais de uma entrada.
Exercício\(\PageIndex{11B}\)
Avalie o seguinte:
- Se cada nota percentual obtida em um curso se traduz em uma nota de uma letra, a nota por letra é uma função da nota percentual?
- Em caso afirmativo, a função é individual?
- Responda
-
a. Sim, a nota por letra é uma função da nota percentual;
b. Não, não é individual. Existem 100 números percentuais diferentes que poderíamos obter, mas apenas cerca de cinco notas de letras possíveis, portanto, não pode haver apenas um número percentual que corresponda a cada nota de letra.
Usando o teste de linha vertical
Como vimos em alguns exemplos acima, podemos representar uma função usando um gráfico. Os gráficos exibem muitos pares de entrada-saída em um espaço pequeno. As informações visuais que eles fornecem geralmente tornam os relacionamentos mais fáceis de entender. Por convenção, os gráficos são normalmente construídos com os valores de entrada ao longo do eixo horizontal e os valores de saída ao longo do eixo vertical.
Os gráficos mais comuns nomeiam o valor de entrada\(x\) e a saída\(y\), e dizemos que\(y\) é uma função de\(x\) ou\(y=f(x)\) quando a função é nomeada\(f\). O gráfico da função é o conjunto de todos os pontos\((x,y)\) no plano que satisfaz a equação\(y=f(x)\). Se a função for definida para apenas alguns valores de entrada, o gráfico da função terá apenas alguns pontos, onde a coordenada x de cada ponto é um valor de entrada e a coordenada y de cada ponto é o valor de saída correspondente. Por exemplo, os pontos pretos no gráfico da Figura nos\(\PageIndex{10}\) dizem que\(f(0)=2\)\(f(6)=1\) e. No entanto, o conjunto de todos os pontos\((x,y)\) que satisfazem\(y=f(x)\) é uma curva. A curva mostrada inclui\((0,2)\) e\((6,1)\) porque a curva passa por esses pontos
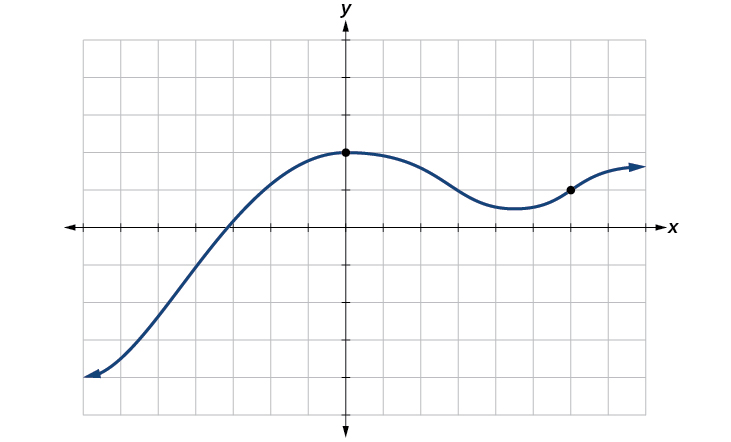
O teste de linha vertical pode ser usado para determinar se um gráfico representa uma função. Se pudermos desenhar qualquer linha vertical que cruze um gráfico mais de uma vez, o gráfico não define uma função porque uma função tem apenas um valor de saída para cada valor de entrada. Veja a Figura\(\PageIndex{11}\).
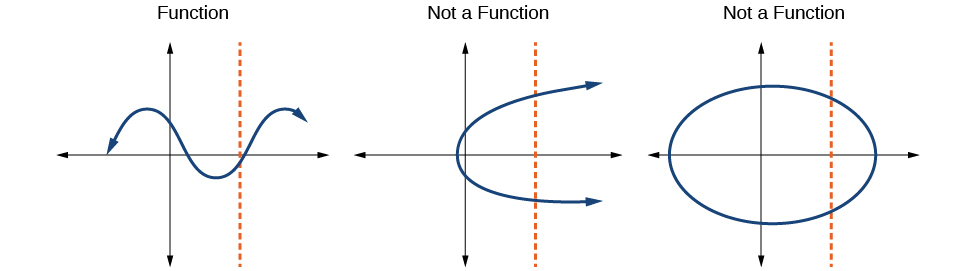
Como fazer: Dado um gráfico, use o teste de linha vertical para determinar se o gráfico representa uma função
- Inspecione o gráfico para ver se alguma linha vertical desenhada cruzaria a curva mais de uma vez.
- Se houver alguma linha desse tipo, determine que o gráfico não representa uma função.
Exemplo\(\PageIndex{12}\): Applying the Vertical Line Test
Qual dos gráficos na Figura\(\PageIndex{12}\) representa (s) uma função\(y=f(x)\)?
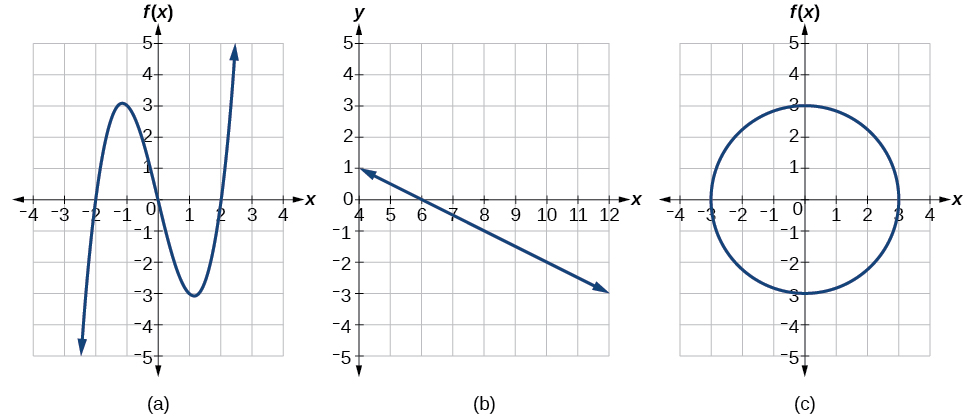
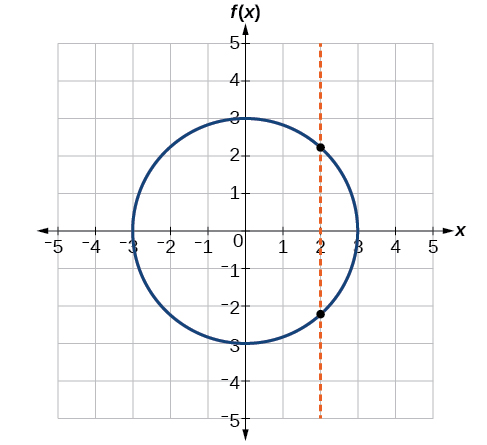
Solução
Se alguma linha vertical cruzar um gráfico mais de uma vez, a relação representada pelo gráfico não é uma função. Observe que qualquer linha vertical passaria por apenas um ponto dos dois gráficos mostrados nas partes (a) e (b) da Figura\(\PageIndex{12}\). A partir disso, podemos concluir que esses dois gráficos representam funções. O terceiro gráfico não representa uma função porque, no máximo, valores de x, uma linha vertical cruzaria o gráfico em mais de um ponto, conforme mostrado na Figura\(\PageIndex{13}\).
Exercício\(\PageIndex{12}\)
O gráfico na Figura\(\PageIndex{14}\) representa uma função?
![[Função absoluta f (x) =|x|.]](https://math.libretexts.org/@api/deki/files/885/CNX_Precalc_Figure_01_02_013.jpg)
- Responda
-
sim
Usando o teste de linha horizontal
Depois de determinarmos que um gráfico define uma função, uma maneira fácil de determinar se é uma função individual é usar o teste de linha horizontal. Desenhe linhas horizontais no gráfico. Se alguma linha horizontal cruzar o gráfico mais de uma vez, o gráfico não representa uma função individual.
Como fazer: Dado um gráfico de uma função, use o teste de linha horizontal para determinar se o gráfico representa uma função individual
- Inspecione o gráfico para ver se alguma linha horizontal desenhada cruzaria a curva mais de uma vez.
- Se houver alguma linha desse tipo, determine que a função não é individual.
Exemplo\(\PageIndex{13}\): Applying the Horizontal Line Test
Considere as funções mostradas na Figura\(\PageIndex{12a}\) e na Figura\(\PageIndex{12b}\). Alguma das funções é individual?
Solução
A função na Figura não\(\PageIndex{12a}\) é individual. A linha horizontal mostrada na Figura\(\PageIndex{15}\) cruza o gráfico da função em dois pontos (e podemos até encontrar linhas horizontais que a cruzam em três pontos).
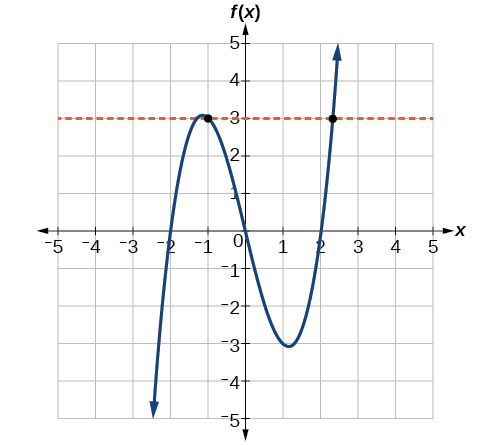
A função na Figura\(\PageIndex{12b}\) é individual. Qualquer linha horizontal cruzará uma linha diagonal no máximo uma vez.
Exercício\(\PageIndex{13}\)
O gráfico mostrado na Figura é\(\PageIndex{13}\) um para um?
- Responda
-
Não, porque não passa no teste da linha horizontal.
Identificação das funções básicas do kit de ferramentas
Neste texto, exploraremos as funções — as formas de seus gráficos, suas características únicas, suas fórmulas algébricas e como resolver problemas com elas. Ao aprender a ler, começamos com o alfabeto. Ao aprender a fazer aritmética, começamos com números. Ao trabalhar com funções, também é útil ter um conjunto básico de elementos de blocos de construção. Nós as chamamos de “funções do kit de ferramentas”, que formam um conjunto de funções nomeadas básicas para as quais conhecemos o gráfico, a fórmula e as propriedades especiais. Algumas dessas funções são programadas para botões individuais em muitas calculadoras. Para essas definições, usaremos x como variável de entrada e\(y=f(x)\) como variável de saída.
Veremos essas funções do kit de ferramentas, combinações de funções do kit de ferramentas, seus gráficos e suas transformações com frequência ao longo deste livro. Será muito útil reconhecer essas funções do kit de ferramentas e seus recursos rapidamente por nome, fórmula, gráfico e propriedades básicas da tabela. Os gráficos e os valores da tabela de amostra estão incluídos em cada função mostrada na Tabela\(\PageIndex{14}\).
| Nome | Função | Gráfico |
|---|---|---|
| Constante | \(f(x)=c\)onde\(c\) é uma constante | 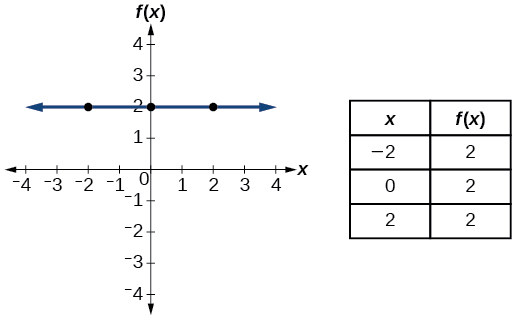 |
| Identidade | \(f(x)=x\) | 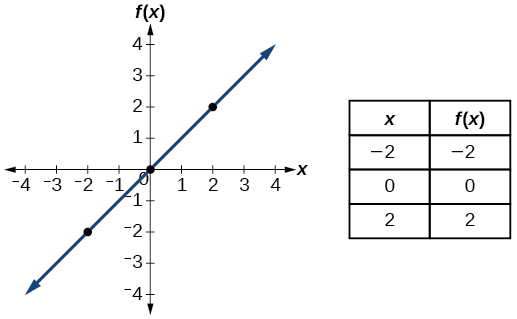 |
| Valor absoluto | \(f(x)=|x|\) | 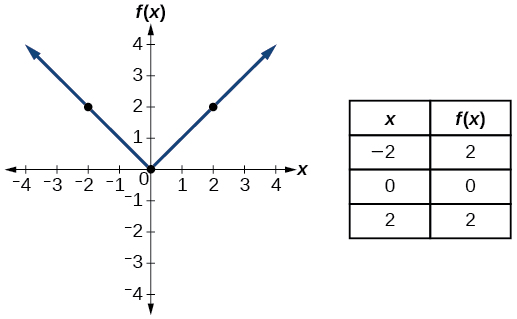 |
| Quadrático | \(f(x)=x^2\) | 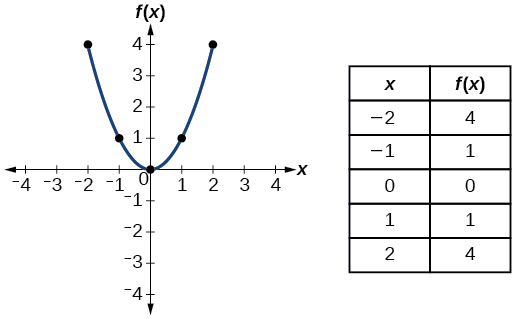 |
| Cúbico | \(f(x)=x^3\) | 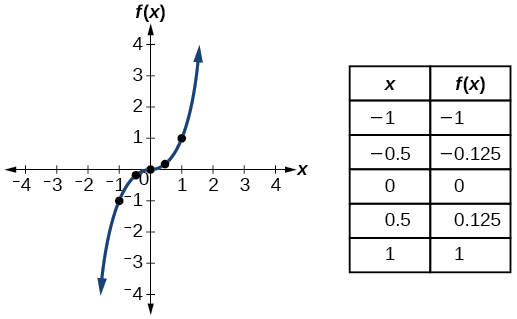 |
| recíproca | \(f(x)=\dfrac{1}{x}\) | 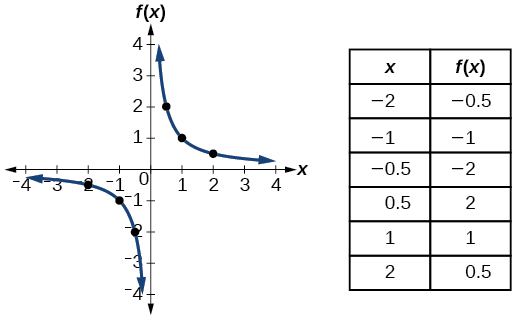 |
| Quadrado recíproco | \(f(x)=\dfrac{1}{x^2}\) | 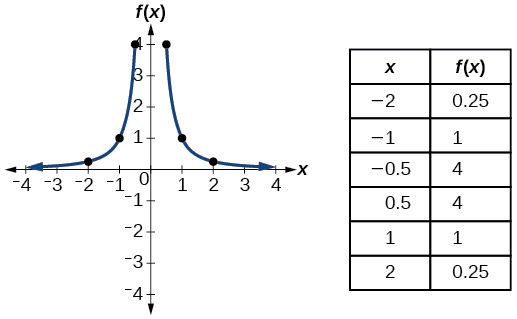 |
| raiz quadrada | \(f(x)=\sqrt{x}\) | 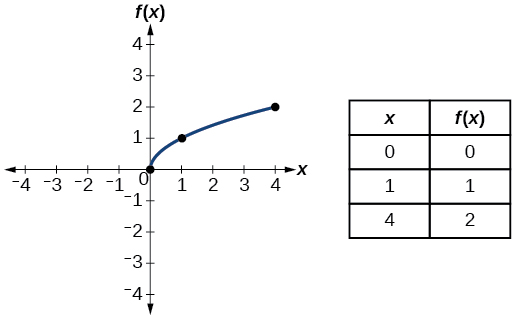 |
| Raiz cúbica | \(f(x)=\sqrt[3]{x}\) | 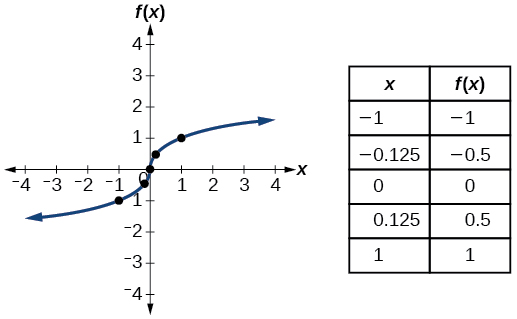 |
Equações chave
- Função constante\(f(x)=c\), onde\(c\) é uma constante
- Função de identidade\(f(x)=x\)
- Função de valor absoluto\(f(x)=|x|\)
- Função quadrática\(f(x)=x^2\)
- Função cúbica\(f(x)=x^3\)
- Função recíproca\(f(x)=\dfrac{1}{x}\)
- Função quadrada recíproca\(f(x)=\frac{1}{x^2}\)
- Função de raiz quadrada\(f(x)=\sqrt{x}\)
- Função de raiz cúbica\(f(x)=3\sqrt{x}\)
Conceitos chave
- Uma relação é um conjunto de pares ordenados. Uma função é um tipo específico de relação em que cada valor de domínio, ou entrada, leva a exatamente um valor de intervalo ou saída.
- A notação de função é um método abreviado para relacionar a entrada à saída no formulário\(y=f(x)\).
- Na forma tabular, uma função pode ser representada por linhas ou colunas relacionadas aos valores de entrada e saída.
- Para avaliar uma função, determinamos um valor de saída para um valor de entrada correspondente. As formas algébricas de uma função podem ser avaliadas substituindo a variável de entrada por um determinado valor.
- Para resolver um valor de função específico, determinamos os valores de entrada que geram o valor de saída específico.
- Uma forma algébrica de uma função pode ser escrita a partir de uma equação.
- Os valores de entrada e saída de uma função podem ser identificados em uma tabela.
- Relacionar valores de entrada com valores de saída em um gráfico é outra forma de avaliar uma função.
- Uma função é individual se cada valor de saída corresponder a apenas um valor de entrada.
- Um gráfico representa uma função se qualquer linha vertical desenhada no gráfico cruzar o gráfico em no máximo um ponto.
- O gráfico de uma função individual passa no teste da linha horizontal.
Notas de pé
1 http://www.baseball-almanac.com/lege... /lisn100.shtml. Acessado em 24/03/2014.
2 www.kgbanswers.com/how-long-i... y-span/4221590. Acessado em 24/03/2014.
Glossário
variável dependente
uma variável de saída
domínio:
o conjunto de todos os valores de entrada possíveis para uma relação
função
uma relação na qual cada valor de entrada produz um valor de saída exclusivo
teste de linha horizontal,
um método para testar se uma função é individual, determinando se alguma linha horizontal cruza o gráfico mais de uma vez
variável independente
uma variável de entrada
insira
cada objeto ou valor em um domínio relacionado a outro objeto ou valor por meio de um relacionamento conhecido como função
função um-para-um
uma função para a qual cada valor da saída está associado a um valor de entrada exclusivo
gera
cada objeto ou valor no intervalo que é produzido quando um valor de entrada é inserido em uma função
intervalo:
o conjunto de valores de saída que resultam dos valores de entrada em uma relação
relação:
um conjunto de pares ordenados
teste de linha vertical:
um método para testar se um gráfico representa uma função determinando se uma linha vertical cruza o gráfico não mais do que uma vez.


