3.6: Transformação de funções
- Page ID
- 189391
Objetivos de
- Funções gráficas usando deslocamentos verticais e horizontais.
- O gráfico funciona usando reflexões sobre o eixo x e o eixo y.
- Determine se uma função é par, ímpar ou nenhuma em seu gráfico.
- Funções gráficas usando compressões e alongamentos.
- Combine transformações.
Todos sabemos que um espelho plano nos permite ver uma imagem precisa de nós mesmos e do que está atrás de nós mesmos. Quando inclinamos o espelho, as imagens que vemos podem mudar horizontal ou verticalmente. Mas o que acontece quando dobramos um espelho flexível? Como um espelho de casa de diversões de carnaval, ele nos apresenta uma imagem distorcida de nós mesmos, esticada ou comprimida horizontal ou verticalmente. Da mesma forma, podemos distorcer ou transformar funções matemáticas para melhor adaptá-las à descrição de objetos ou processos no mundo real. Nesta seção, veremos vários tipos de transformações.

Muitas vezes, quando temos um problema, tentamos modelar o cenário usando matemática na forma de palavras, tabelas, gráficos e equações. Um método que podemos empregar é adaptar os gráficos básicos das funções do kit de ferramentas para criar novos modelos para um determinado cenário. Existem formas sistemáticas de alterar funções para construir modelos apropriados para os problemas que estamos tentando resolver.
Identificação de mudanças verticais
Um tipo simples de transformação envolve deslocar o gráfico inteiro de uma função para cima, para baixo, para a direita ou para a esquerda. O deslocamento mais simples é um deslocamento vertical, movendo o gráfico para cima ou para baixo, porque essa transformação envolve a adição de uma constante positiva ou negativa à função. Em outras palavras, adicionamos a mesma constante ao valor de saída da função, independentemente da entrada. Para uma função\(g(x)=f(x)+k\), a função\(f(x)\) é deslocada verticalmente em\(k\) unidades. Veja a Figura\(\PageIndex{2}\) para obter um exemplo.
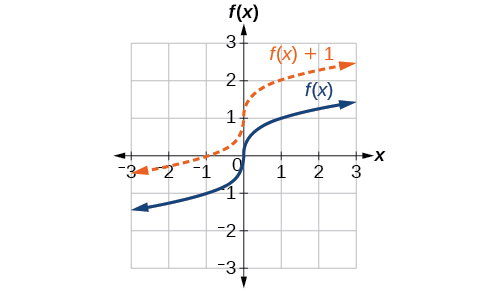
Para ajudá-lo a visualizar o conceito de mudança vertical, considere isso\(y=f(x)\). Portanto,\(f(x)+k\) é equivalente\(y+k\) a. Cada unidade de\(y\) é substituída por\(y+k\), então o\(y\) valor -aumenta ou diminui dependendo do valor de\(k\). O resultado é uma mudança para cima ou para baixo.
Definição: Deslocamento vertical
Dada uma função\(f(x)\), uma nova função\(g(x)=f(x)+k\), onde\(k\) é uma constante, é um deslocamento vertical da função\(f(x)\). Todos os valores de saída mudam por\(k\) unidades. Se\(k\) for positivo, o gráfico mudará para cima. Se\(k\) for negativo, o gráfico se deslocará para baixo.
Exemplo\(\PageIndex{1}\): Adding a Constant to a Function
Para regular a temperatura em um prédio verde, as aberturas de fluxo de ar próximas ao telhado abrem e fecham durante todo o dia. A figura\(\PageIndex{3}\) mostra a área de aberturas abertas\(V\) (em pés quadrados) ao longo do dia em horas após a meia-noite,\(t\). Durante o verão, o gerente das instalações decide tentar regular melhor a temperatura aumentando a quantidade de aberturas abertas em 20 pés quadrados durante o dia e a noite. Esboce um gráfico dessa nova função.
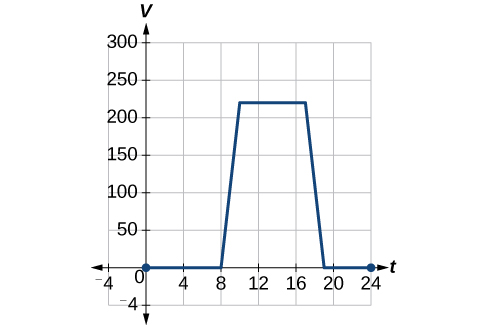
Solução
Podemos esboçar um gráfico dessa nova função adicionando 20 a cada um dos valores de saída da função original. Isso terá o efeito de deslocar o gráfico verticalmente para cima, conforme mostrado na Figura\(\PageIndex{4}\).
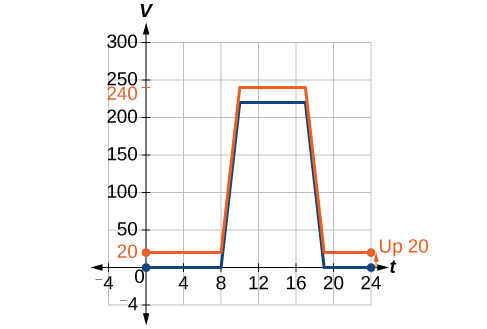
Observe que na Figura\(\PageIndex{4}\), para cada valor de entrada, o valor de saída aumentou em 20, portanto, se chamarmos a nova função\(S(t)\), poderíamos escrever
\[S(t)=V(t)+20\]
Essa notação nos diz que, para qualquer valor de\(t\),\(S(t)\) pode ser encontrado avaliando a função\(V\) na mesma entrada e adicionando 20 ao resultado. Isso define\(S\) como uma transformação da função\(V\), neste caso, um deslocamento vertical até 20 unidades. Observe que, com um deslocamento vertical, os valores de entrada permanecem os mesmos e somente os valores de saída mudam. Veja a tabela\(\PageIndex{1}\).
| \(t\) | 0 | 8 | 10 | 17 | 19 | 24 |
|---|---|---|---|---|---|---|
| \(V(t)\) | 0 | 0 | 220 | 220 | 0 | 0 |
| \(S(t)\) | 20 | 20 | 240 | 240 | 20 | 20 |
Como...
Dada uma função tabular, crie uma nova linha para representar um deslocamento vertical.
- Identifique a linha ou coluna de saída.
- Determine a magnitude da mudança.
- Adicione a mudança ao valor em cada célula de saída. Adicione um valor positivo para cima ou um valor negativo para baixo.
Exemplo\(\PageIndex{2}\): Shifting a Tabular Function Vertically
Uma função\(f(x)\) é fornecida na Tabela\(\PageIndex{2}\). Crie uma tabela para a função\(g(x)=f(x)−3\).
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(f(x)\) | 1 | 3 | 7 | 11 |
Solução
A fórmula nos\(g(x)=f(x)−3\) diz que podemos encontrar os valores de saída\(g\) de subtraindo 3 dos valores de saída de\(f\). Por exemplo:
\[\begin{align*} f(x)&=1 &\text{Given} \\[4pt] g(x)&=f(x)-3 &\text{Given Transformation} \\[4pt] g(2) & =f(2)−3 \\ &=1-3\\ &=-2\end{align*}\]
Subtraindo 3 de cada\(f(x)\) valor, podemos completar uma tabela de valores para\(g(x)\) conforme mostrado na Tabela\(\PageIndex{3}\).
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(f(x)\) | 1 | 3 | 7 | 11 |
| \(g(x)\) | -2 | 0 | 4 | 8 |
Análise
Como no deslocamento vertical anterior, observe que os valores de entrada permanecem os mesmos e somente os valores de saída mudam.
Exercício\(\PageIndex{1}\)
A função\(h(t)=−4.9t^2+30t\) fornece a altura\(h\) de uma bola (em metros) lançada do chão para cima após\(t\) segundos. Suponha que a bola tenha sido lançada do topo de um prédio de 10 metros. Relacione essa nova função de altura\(b(t)\) com e\(h(t)\), em seguida, encontre uma fórmula para\(b(t)\).
- Resposta
-
\(b(t)=h(t)+10=−4.9t^2+30t+10\)
Identificação de mudanças horizontais
Acabamos de ver que o deslocamento vertical é uma mudança na saída, ou fora, da função. Agora veremos como as mudanças na entrada, no interior da função, alteram seu gráfico e significado. Uma mudança na entrada resulta em um movimento do gráfico da função para a esquerda ou para a direita no que é conhecido como deslocamento horizontal, mostrado na Figura\(\PageIndex{4}\).
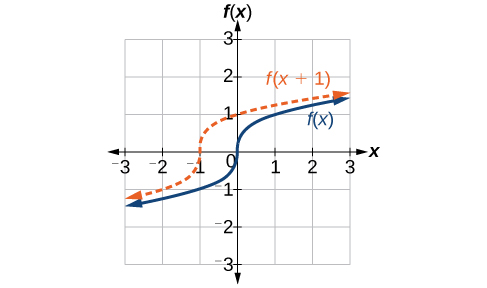
Por exemplo, if\(f(x)=x^2\), então\(g(x)=(x−2)^2\) é uma nova função. Cada entrada é reduzida em 2 antes de colocar a função ao quadrado. O resultado é que o gráfico é deslocado 2 unidades para a direita, porque precisaríamos aumentar a entrada anterior em 2 unidades para produzir o mesmo valor de saída fornecido em\(f\).
Definição: Deslocamento horizontal
Dada uma função\(f\), uma nova função\(g(x)=f(x−h)\), onde\(h\) é uma constante, é um deslocamento horizontal da função\(f\). Se\(h\) for positivo, o gráfico mudará para a direita. Se\(h\) for negativo, o gráfico mudará para a esquerda.
Exemplo\(\PageIndex{4}\): Adding a Constant to an Input
Voltando ao nosso exemplo de fluxo de ar do prédio da Figura\(\PageIndex{2}\), suponha que no outono o gerente das instalações decida que o plano de ventilação original comece tarde demais e queira iniciar todo o programa de ventilação 2 horas antes. Esboce um gráfico da nova função.
Solução
Podemos\(V(t)\) definir como o programa original e\(F(t)\) o programa revisado.
\[V(t)= \text{ the original venting plan} \nonumber\]
\[F(t)= \text{ starting 2 hrs sooner} \nonumber\]
No novo gráfico, a cada vez, o fluxo de ar é o mesmo da função\(V\) original 2 horas depois. Por exemplo, na função original\(V\), o fluxo de ar começa a mudar às 8 da manhã, enquanto para a função\(F\), o fluxo de ar começa a mudar às 6 da manhã. Os valores de função comparáveis são\(V(8)=F(6)\). Veja a Figura\(\PageIndex{5}\). Observe também que as aberturas abriram pela primeira vez\(220 \text{ft}^2\) às 10h de acordo com o plano original, enquanto no novo plano as aberturas chegam\(220 \text{ft}^2\) às 8h, então\(V(10)=F(8)\).
Em ambos os casos, vemos isso, porque\(F(t)\) começa 2 horas mais cedo,\(h=−2\). Isso significa que os mesmos valores de saída são alcançados quando\(F(t)=V(t−(−2))=V(t+2)\).
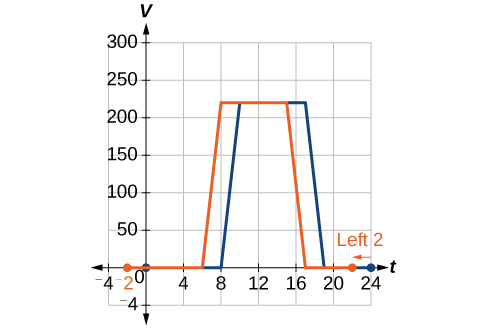
Análise
Observe que isso\(V(t+2)\) tem o efeito de deslocar o gráfico para a esquerda.
Mudanças horizontais ou “mudanças internas” afetam o domínio de uma função (a entrada) em vez do alcance e geralmente parecem contra-intuitivas. A nova função\(F(t)\) usa as mesmas saídas de\(V(t)\), mas combina essas saídas com as entradas 2 horas antes das de\(V(t)\). Dito de outra forma, devemos adicionar 2 horas à entrada de\(V\) para encontrar a saída correspondente para\(F:F(t)=V(t+2)\).
Como...
Dada uma função tabular, crie uma nova linha para representar um deslocamento horizontal.
- Identifique a linha ou coluna de entrada.
- Determine a magnitude da mudança.
- Adicione a mudança ao valor em cada célula de entrada.
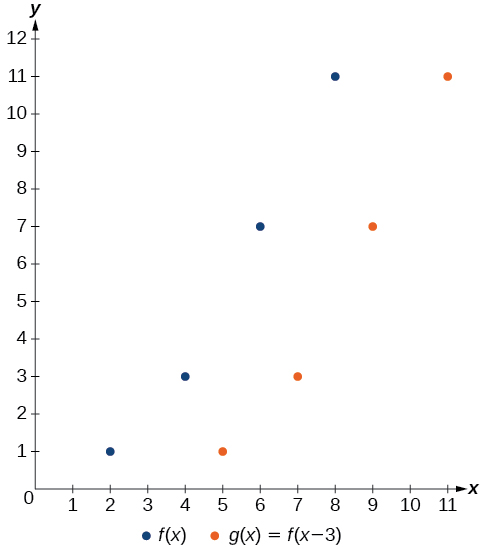
Exemplo\(\PageIndex{5}\): Shifting a Tabular Function Horizontally
Uma função\(f(x)\) é fornecida na Tabela\(\PageIndex{4}\). Crie uma tabela para a função\(g(x)=f(x−3)\).
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(f(x)\) | 1 | 3 | 7 | 11 |
Solução
A fórmula nos\(g(x)=f(x−3)\) diz que os valores de saída de\(g\) são iguais ao valor de saída de\(f\) quando o valor de entrada é 3 a menos que o valor original. Por exemplo, sabemos disso\(f(2)=1\). Para obter a mesma saída da função\(g\), precisaremos de um valor de entrada 3 maior. Nós inserimos um valor 3 maior para\(g(x)\) porque a função retira 3 antes de avaliá-la\(f\).
\[\begin{align*} g(5)&=f(5-3) \\ &=f(2) \\ &=1 \end{align*}\]
Continuamos com os outros valores para criar a tabela\(\PageIndex{5}\).
| \(x\) | 5 | 7 | 9 | 11 |
|---|---|---|---|---|
| \(x-3\) | 2 | 4 | 6 | 8 |
| \(f(x)\) | 1 | 3 | 7 | 11 |
| \(g(x)\) | 1 | 3 | 7 | 11 |
O resultado é que a função\(g(x)\) foi deslocada para a direita em 3. Observe que os valores de saída para\(g(x)\) permanecem os mesmos que os valores de saída para\(f(x)\), mas os valores de entrada correspondentes\(x\),, foram deslocados para a direita em 3. Especificamente, 2 mudou para 5, 4 mudou para 7, 6 mudou para 9 e 8 mudou para 11.
Análise
\(\PageIndex{6}\)A figura representa as duas funções. Podemos ver a mudança horizontal em cada ponto.
Exemplo\(\PageIndex{6}\): Identifying a Horizontal Shift of a Toolkit Function
\(\PageIndex{7}\)A figura representa uma transformação da função do kit de ferramentas\(f(x)=x^2\). Relacione essa nova função\(g(x)\) com e\(f(x)\), em seguida, encontre uma fórmula para\(g(x)\).
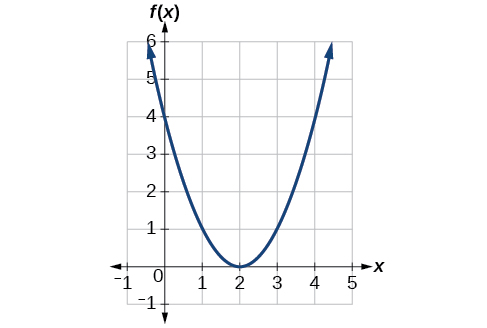
Solução
Observe que o gráfico tem a mesma forma da\(f(x)=x^2\) função, mas os\(x\) valores -são deslocados para as 2 unidades à direita. O vértice costumava estar em\((0,0)\), mas agora o vértice está em\((2,0)\). O gráfico é a função quadrática básica deslocada 2 unidades para a direita, então
\[g(x)=f(x−2) \nonumber\]
Observe como devemos inserir o valor\(x=2\) para obter o valor de saída\(y=0\); os\(x\) valores -devem ser 2 unidades maiores devido à mudança de 2 unidades para a direita. Podemos então usar a definição da\(f(x)\) função para escrever uma fórmula\(g(x)\) por meio da avaliação\(f(x−2)\).
\[\begin{align*} f(x)&=x^2 \\ g(x)&=f(x-2) \\ g(x)&=f(x-2)=(x-2)^2 \end{align*}\]
Análise
Para determinar se a mudança é\(+2\) ou\(−2\), considere um único ponto de referência no gráfico. Para uma quadrática, observar o ponto do vértice é conveniente. Na função original,\(f(0)=0\). Em nossa função deslocada,\(g(2)=0\). Para obter o valor de saída de 0 da função\(f\), precisamos decidir se um sinal de mais ou menos funcionará para satisfazer\(g(2)=f(x−2)=f(0)=0\). Para que isso funcione, precisaremos subtrair 2 unidades dos nossos valores de entrada.
Exemplo\(\PageIndex{7}\): Interpreting Horizontal versus Vertical Shifts
A função\(G(m)\) fornece o número de galões de gasolina necessários para percorrer\(m\) milhas. Interpretar\(G(m)+10\) e\(G(m+10)\)
Solução
\(G(m)+10\)pode ser interpretado como adicionar 10 à saída, galões. Este é o gás necessário para percorrer\(m\) milhas, além de outros 10 galões de gasolina. O gráfico indicaria uma mudança vertical.
\(G(m+10)\)pode ser interpretado como adicionar 10 à entrada, milhas. Portanto, esse é o número de galões de gasolina necessários para dirigir 10 milhas a mais do que\(m\) milhas. O gráfico indicaria uma mudança horizontal.
Exercício\(\PageIndex{7}\)
Dada a função\(f(x)=\sqrt{x}\), represente graficamente a função original\(f(x)\) e a transformação\(g(x)=f(x+2)\) nos mesmos eixos. Isso é uma mudança horizontal ou vertical? Para que lado o gráfico é deslocado e em quantas unidades?
- Resposta
-
Os gráficos de\(f(x)\) e\(g(x)\) são mostrados abaixo. A transformação é uma mudança horizontal. A função é deslocada para a esquerda em 2 unidades.
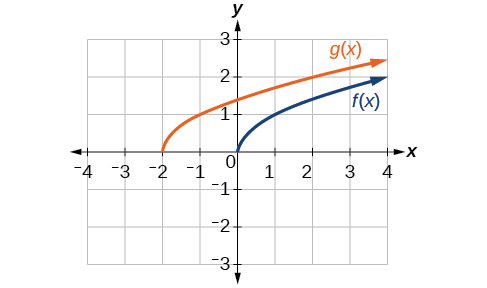
Figura\(\PageIndex{8}\)
Combinando mudanças verticais e horizontais
Agora que temos duas transformações, podemos combiná-las. Os deslocamentos verticais são mudanças externas que afetam os valores do\((y-)\) eixo de saída e deslocam a função para cima ou para baixo. Os deslocamentos horizontais são alterações internas que afetam os valores do\((x-)\) eixo de entrada e deslocam a função para a esquerda ou para a direita. A combinação dos dois tipos de mudanças fará com que o gráfico de uma função mude para cima ou para baixo e para a direita ou para a esquerda.
Como...
Dada uma função e um deslocamento vertical e horizontal, desenhe o gráfico.
- Identifique os desvios verticais e horizontais da fórmula.
- O deslocamento vertical resulta de uma constante adicionada à saída. Mova o gráfico para cima para uma constante positiva e para baixo para uma constante negativa.
- O deslocamento horizontal resulta de uma constante adicionada à entrada. Mova o gráfico para a esquerda para uma constante positiva e para a direita para uma constante negativa.
- Aplique os deslocamentos ao gráfico em qualquer ordem.
Exemplo\(\PageIndex{8}\): Graphing Combined Vertical and Horizontal Shifts
Dado\(f(x)=|x|\), esboce um gráfico de\(h(x)=f(x+1)−3\).
Solução
A função\(f\) é a função de valor absoluto do nosso kit de ferramentas. Sabemos que esse gráfico tem uma forma de V, com o ponto na origem. O gráfico de se\(h\) transformou\(f\) de duas maneiras:\(f(x+1)\) é uma mudança no interior da função, dando um deslocamento horizontal à esquerda em 1, e a subtração em 3 in\(f(x+1)−3\) é uma mudança na parte externa da função, dando um deslocamento vertical para baixo em 3. A transformação do gráfico é ilustrada na Figura\(\PageIndex{9}\).
Vamos seguir um ponto do gráfico de\(f(x)=|x|\).
- O ponto\((0,0)\) é transformado primeiro deslocando para a esquerda 1 unidade:\((0,0)\rightarrow(−1,0)\)
- O ponto\((−1,0)\) é transformado em seguida, deslocando 3 unidades para baixo:\((−1,0)\rightarrow(−1,−3)\)
A figura\(\PageIndex{10}\) mostra o gráfico de\(h\).
Exercício\(\PageIndex{8}\)
Dado\(f(x)=|x|\), esboce um gráfico de\(h(x)=f(x−2)+4\).
- Resposta
-
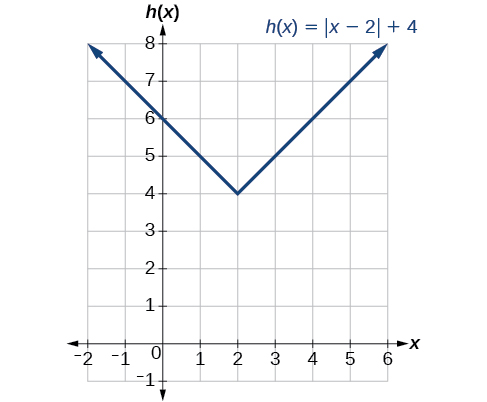
Figura\(\PageIndex{11}\)
Exemplo\(\PageIndex{9}\): Identifying Combined Vertical and Horizontal Shifts
Escreva uma fórmula para o gráfico mostrado na Figura\(\PageIndex{12}\), que é uma transformação da função de raiz quadrada do kit de ferramentas.
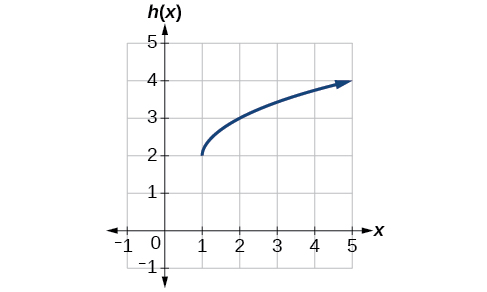
Solução
O gráfico da função do kit de ferramentas começa na origem, então esse gráfico foi deslocado 1 para a direita e para cima 2. Na notação de função, poderíamos escrever isso como
\[h(x)=f(x−1)+2 \nonumber\]
Usando a fórmula para a função de raiz quadrada, podemos escrever
\[h(x)=\sqrt{x−1}+2 \nonumber\]
Análise
Observe que essa transformação alterou o domínio e o alcance da função. Esse novo gráfico tem domínio\(\left[1,\infty\right)\) e alcance\(\left[2,\infty\right)\).
Exercício\(\PageIndex{9}\)
Escreva uma fórmula para uma transformação da função recíproca do kit de ferramentas\(f(x)=\frac{1}{x}\) que desloca o gráfico da função uma unidade para a direita e uma unidade para cima.
- Resposta
-
\[g(x)=\dfrac{1}{x-1}+1 \nonumber \]
Funções gráficas usando reflexões sobre os eixos
Outra transformação que pode ser aplicada a uma função é uma reflexão sobre o eixo x ou y. Uma reflexão vertical reflete um gráfico verticalmente no eixo x, enquanto uma reflexão horizontal reflete um gráfico horizontalmente no eixo y. As reflexões são mostradas na Figura\(\PageIndex{13}\).
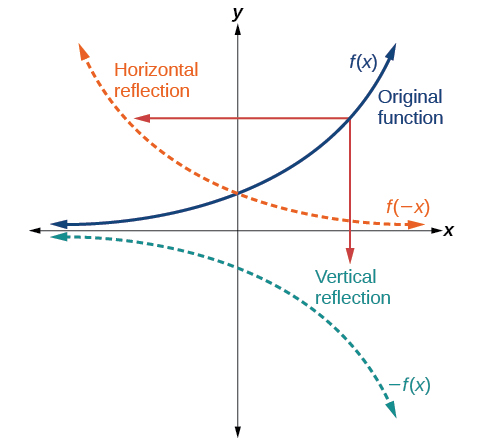 .
.
Observe que a reflexão vertical produz um novo gráfico que é uma imagem espelhada da base ou do gráfico original sobre o eixo x. A reflexão horizontal produz um novo gráfico que é uma imagem espelhada da base ou gráfico original sobre o eixo y.
Definições: Reflexões
Dada uma função\(f(x)\), uma nova função\(g(x)=−f(x)\) é um reflexo vertical da função\(f(x)\), às vezes chamada de reflexão sobre (ou sobre ou através) do eixo x.
Dada uma função\(f(x)\), uma nova função\(g(x)=f(−x)\) é uma reflexão horizontal da função\(f(x)\), às vezes chamada de reflexão sobre o eixo y.
Como...
Dada uma função, reflita o gráfico na vertical e na horizontal.
- Multiplique todas as saídas por —1 para uma reflexão vertical. O novo gráfico é um reflexo do gráfico original sobre o eixo x.
- Multiplique todas as entradas por —1 para uma reflexão horizontal. O novo gráfico é um reflexo do gráfico original sobre o eixo y.
Exemplo\(\PageIndex{10}\): Reflecting a Graph Horizontally and Vertically
Reflita o gráfico de\(s(t)=\sqrt{t}\) (a) na vertical e (b) na horizontal.
Solução
a. Refletir o gráfico verticalmente significa que cada valor de saída será refletido sobre o eixo t horizontal, conforme mostrado na Figura\(\PageIndex{14}\).
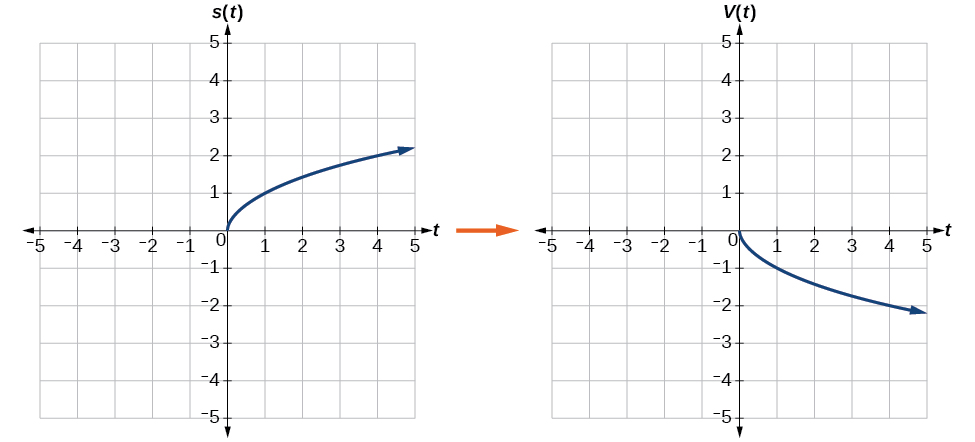
Como cada valor de saída é o oposto do valor de saída original, podemos escrever
\[V(t)=−s(t) \text{ or } V(t)=−\sqrt{t} \nonumber\]
Observe que essa é uma alteração externa, ou mudança vertical, que afeta os\(s(t)\) valores de saída, portanto, o sinal negativo pertence fora da função.
b. Refletir horizontalmente significa que cada valor de entrada será refletido sobre o eixo vertical, conforme mostrado na Figura\(\PageIndex{15}\).
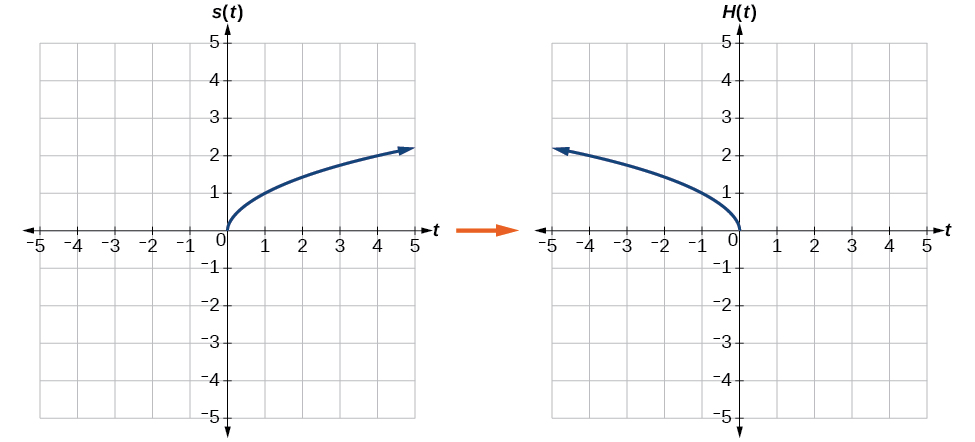
Como cada valor de entrada é o oposto do valor de entrada original, podemos escrever
\[H(t)=s(−t) \text{ or } H(t)=\sqrt{−t} \nonumber\]
Observe que essa é uma mudança interna ou horizontal que afeta os valores de entrada, então o sinal negativo está na parte interna da função.
Observe que essas transformações podem afetar o domínio e o alcance das funções. Enquanto a função de raiz quadrada original tem domínio\(\left[0,\infty\right)\) e alcance\(\left[0,\infty\right)\), a reflexão vertical dá à\(V(t)\) função o alcance\(\left(−\infty,0\right]\) e a reflexão horizontal dá à\(H(t)\) função o domínio\(\left(−\infty, 0\right]\).
Exercício\(\PageIndex{5}\)
Reflita o gráfico de\(f(x)=|x−1|\) (a) na vertical e (b) na horizontal.
- Resposta
-
uma.
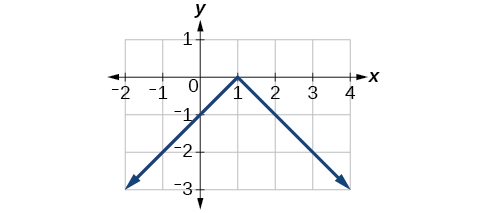
Figura\(\PageIndex{16}\): Gráfico de uma função absoluta refletida verticalmente. b.
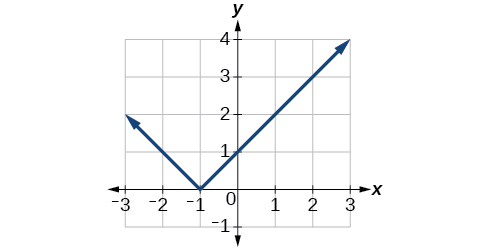
Figura\(\PageIndex{17}\): Gráfico de uma função absoluta traduzida uma unidade à esquerda.
Exemplo\(\PageIndex{11}\): Reflecting a Tabular Function Horizontally and Vertically
Uma função\(f(x)\) é fornecida como Tabela\(\PageIndex{6}\). Crie uma tabela para as funções abaixo.
a.\(g(x)=−f(x)\)
b.\(h(x)=f(−x)\)
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(f(x)\) | 1 | 3 | 7 | 11 |
a. Para\(g(x)\), o sinal negativo fora da função indica uma reflexão vertical, então os valores de x permanecem os mesmos e cada valor de saída será o oposto do valor de saída original. Veja a tabela\(\PageIndex{7}\).
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(g(x)\) | -1 | -3 | -7 | -11 |
b. Para\(h(x)\), o sinal negativo dentro da função indica uma reflexão horizontal, então cada valor de entrada será o oposto do valor de entrada original e os\(h(x)\) valores permanecerão iguais aos\(f(x)\) valores. Veja a tabela\(\PageIndex{8}\).
| \(x\) | -2 | -4 | -6 | -8 |
|---|---|---|---|---|
| \(h(x)\) | 1 | 3 | 7 | 11 |
Exercício\(\PageIndex{6}\)
Uma função\(f(x)\) é fornecida como Tabela\(\PageIndex{9}\). Crie uma tabela para as funções abaixo.
a.\(g(x)=−f(x)\)
b.\(h(x)=f(−x)\)
| \(x\) | -2 | 0 | 2 | 4 |
|---|---|---|---|---|
| \(f(x)\) | 5 | 10 | 15 | 20 |
- Resposta
-
uma.\(g(x)=−f(x)\)
Tabela\(\PageIndex{10}\) \(x\) -2 0 2 4 \(g(x)\) -5 -10 -15 -20 b.\(h(x)=f(−x)\)
Tabela\(\PageIndex{11}\) \(x\) -2 0 2 -4 \(h(x)\) 15 10 5 20
Exemplo\(\PageIndex{12}\): Applying a Learning Model Equation
Um modelo comum de aprendizagem tem uma equação semelhante a\(k(t)=−2^{−t}+1\), onde\(k\) está a porcentagem de domínio que pode ser alcançada após as sessões\(t\) práticas. Essa é uma transformação da função\(f(t)=2^t\) mostrada na Figura\(\PageIndex{18}\). Esboce um gráfico de\(k(t)\).
Solução
Essa equação combina três transformações em uma equação.
- Uma reflexão horizontal:\(f(−t)=2^{−t}\)
- Uma reflexão vertical:\(−f(−t)=−2^{−t}\)
- Uma mudança vertical:\(−f(−t)+1=−2^{−t}+1\)
Podemos esboçar um gráfico aplicando essas transformações uma de cada vez à função original. Vamos seguir dois pontos em cada uma das três transformações. Escolheremos os pontos\((0, 1)\)\((1, 2)\) e.
- Primeiro, aplicamos uma reflexão horizontal:\((0, 1) \; (–1, 2)\).
- Então, aplicamos uma reflexão vertical:\((0, −1) \; (-1, –2)\).
- Finalmente, aplicamos uma mudança vertical:\((0, 0) \; (-1, -1)\).
Isso significa que os pontos originais\((0,1)\) e\((1,2)\) se tornam\((0,0)\) e\((-1,-1)\) depois de aplicarmos as transformações.
Na Figura\(\PageIndex{19}\), o primeiro gráfico resulta de uma reflexão horizontal. O segundo resulta de uma reflexão vertical. O terceiro resulta de uma mudança vertical para cima de 1 unidade.
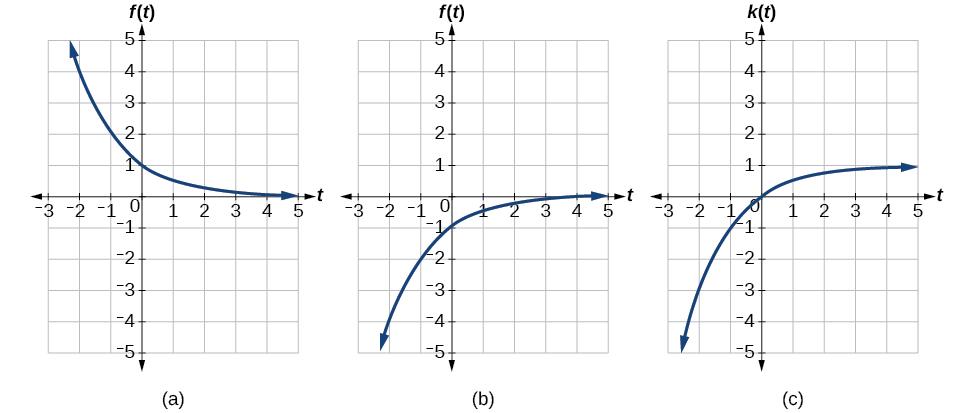
Análise
Como modelo de aprendizagem, essa função seria limitada a um domínio de\(t\geq0\), com alcance correspondente\(\left[0,1\right)\).
Exercício\(\PageIndex{7}\)
Dada a função do kit de ferramentas\(f(x)=x^2\), gráfico\(g(x)=−f(x)\)\(h(x)=f(−x)\) e. Anote qualquer comportamento surpreendente dessas funções.
- Resposta
-
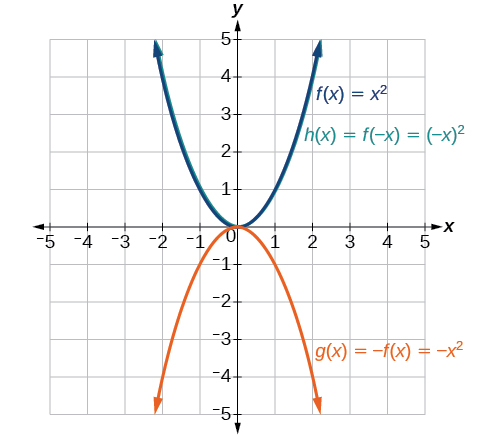
Figura\(\PageIndex{20}\): Gráfico\(x^2\) e suas reflexões. Aviso:\(g(x)=f(−x)\) parece o mesmo que\(f(x)\).
Determinando funções pares e ímpares
Algumas funções exibem simetria, de modo que os reflexos resultam no gráfico original. Por exemplo, refletir horizontalmente as funções do kit de ferramentas\(f(x)=x^2\) ou\(f(x)=|x|\) resultará no gráfico original. Dizemos que esses tipos de gráficos são simétricos em relação ao eixo y. Funções cujos gráficos são simétricos em relação ao eixo y são chamadas de funções pares.
Se os gráficos de\(f(x)=x^3\) ou\(f(x)=\frac{1}{x}\) fossem refletidos em ambos os eixos, o resultado seria o gráfico original, conforme mostrado na Figura\(\PageIndex{21}\).
Dizemos que esses gráficos são simétricos quanto à origem. Uma função com um gráfico simétrico em relação à origem é chamada de função ímpar.
Nota: Uma função não pode ser nem par nem ímpar se não exibir nenhuma simetria. Por exemplo, não\(f(x)=2^x\) é par nem ímpar. Além disso, a única função que é par e ímpar é a função constante\(f(x)=0\).
Definições: Funções pares e ímpares
Uma função é chamada de função par se para cada entrada\(x\)
\(f(x)=f(−x)\)
O gráfico de uma função par é simétrico em relação ao eixo y.
Uma função é chamada de função ímpar se for para cada entrada\(x\)
\(f(x)=−f(−x)\)
O gráfico de uma função ímpar é simétrico em relação à origem.
Como...
Dada a fórmula de uma função, determine se a função é par, ímpar ou nenhuma.
- Determine se a função é satisfatória\(f(x)=f(−x)\). Se isso acontecer, está empatado.
- Determine se a função é satisfatória\(f(x)=−f(−x)\). Se isso acontecer, é estranho.
- Se a função não satisfizer nenhuma das regras, ela não será nem par nem ímpar.
Exemplo\(\PageIndex{13}\): Determining whether a Function Is Even, Odd, or Neither
A função é\(f(x)=x^3+2x\) par, ímpar ou nenhuma?
Solução
Sem olhar para um gráfico, podemos determinar se a função é par ou ímpar encontrando fórmulas para as reflexões e determinando se elas nos retornam à função original. Vamos começar com a regra para funções pares.
\[f(−x)=(−x)^3+2(−x)=−x^3−2x \nonumber\]
Isso não nos retorna à função original, então essa função não é uniforme. Agora podemos testar a regra para funções ímpares.
\[−f(−x)=−(−x^3−2x)=x^3+2x \nonumber\]
Porque\(−f(−x)=f(x)\) essa é uma função estranha.
Análise
Considere o gráfico de\(f\) na Figura\(\PageIndex{22}\). Observe que o gráfico é simétrico em relação à origem. Para cada ponto\((x,y)\) no gráfico, o ponto correspondente também\((−x,−y)\) está no gráfico. Por exemplo,\((1, 3)\) está no gráfico de\(f\), e o ponto correspondente também\((−1,−3)\) está no gráfico.
Exercício\(\PageIndex{8}\)
A função é\(f(s)=s^4+3s^2+7\) par, ímpar ou nenhuma?
- Resposta
-
uniforme
Funções gráficas usando alongamentos e compressões
Adicionar uma constante às entradas ou saídas de uma função alterou a posição de um gráfico em relação aos eixos, mas não afetou a forma de um gráfico. Agora, exploramos os efeitos da multiplicação das entradas ou saídas por alguma quantidade.
Podemos transformar o interior (valores de entrada) de uma função ou podemos transformar o exterior (valores de saída) de uma função. Cada alteração tem um efeito específico que pode ser visto graficamente.
Alongamentos e compressões verticais
Quando multiplicamos uma função por uma constante positiva, obtemos uma função cujo gráfico é esticado ou comprimido verticalmente em relação ao gráfico da função original. Se a constante for maior que 1, obtemos um alongamento vertical; se a constante estiver entre 0 e 1, obtemos uma compressão vertical. A figura\(\PageIndex{23}\) mostra uma função multiplicada pelos fatores constantes 2 e 0,5 e o alongamento e compressão verticais resultantes.
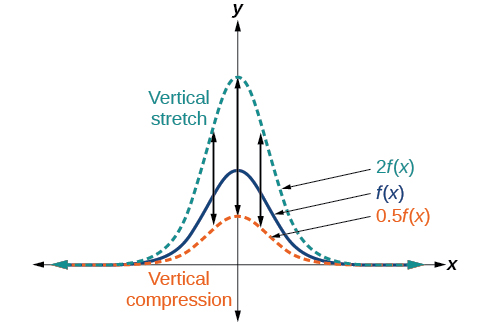
Definições: alongamentos e compressões verticais
Dada uma função\(f(x)\), uma nova função\(g(x)=af(x)\), onde\(a\) é uma constante, é um alongamento vertical ou compressão vertical da função\(f(x)\).
- Se\(a>1\) sim, então o gráfico será esticado.
- Se\(0<a<1\) sim, então o gráfico será compactado.
- Se\(a<0\), então haverá uma combinação de um estiramento ou compressão vertical com uma reflexão vertical.
Como...
Dada uma função, represente graficamente sua extensão vertical.
- Identifique o valor de\(a\).
- Multiplique todos os valores do intervalo por\(a\)
- Se\(a>1\), o gráfico é esticado por um fator de\(a\).
- Se\(0<a<1\), o gráfico é comprimido por um fator de\(a\).
- Se\(a<0\), o gráfico está esticado ou comprimido e também é refletido sobre o eixo x.
Exemplo 1.5.14: Representação gráfica de um trecho vertical
Uma função\(P(t)\) modela a população de moscas-das-frutas. O gráfico é mostrado na Figura\(\PageIndex{24}\).
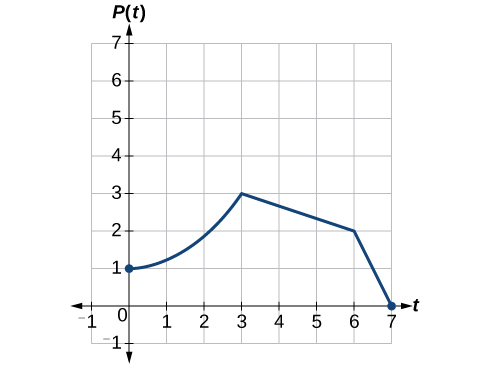
Um cientista está comparando essa população com outra população\(Q\), cujo crescimento segue o mesmo padrão, mas é duas vezes maior. Esboce um gráfico dessa população.
Solução
Como a população é sempre duas vezes maior, os valores de saída da nova população são sempre o dobro dos valores de saída da função original. Graficamente, isso é mostrado na Figura\(\PageIndex{25}\).
Se escolhermos quatro pontos de referência\((0, 1)\)\((3, 3)\),,,\((6, 2)\) e\((7, 0)\) multiplicaremos todas as saídas por 2.
O seguinte mostra onde os novos pontos do novo gráfico estarão localizados.
\[(0, 1)\rightarrow(0, 2)\]
\[(3, 3)\rightarrow(3, 6)\]
\[(6, 2)\rightarrow(6, 4)\]
\[(7, 0)\rightarrow(7, 0)\]
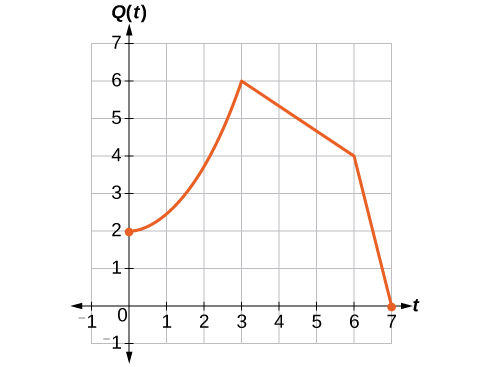
Simbolicamente, o relacionamento é escrito como
\[Q(t)=2P(t) \nonumber\]
Isso significa que, para qualquer entrada\(t\), o valor da função\(Q\) é o dobro do valor da função\(P\). Observe que o efeito no gráfico é um alongamento vertical do gráfico, em que cada ponto dobra sua distância do eixo horizontal. Os valores de entrada,\(t\), permanecem os mesmos, enquanto os valores de saída são duas vezes maiores do que antes.
Como...
Dada uma função tabular e supondo que a transformação seja um alongamento ou compressão vertical, crie uma tabela para uma compressão vertical.
- Determine o valor de\(a\).
- Multiplique todos os valores de saída por\(a\).
Exemplo\(\PageIndex{15}\): Finding a Vertical Compression of a Tabular Function
Uma função\(f\) é fornecida como Tabela\(\PageIndex{12}\). Crie uma tabela para a função\(g(x)=\frac{1}{2}f(x)\).
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(f(x)\) | 1 | 3 | 7 | 11 |
Solução
A fórmula nos\(g(x)=\frac{1}{2}f(x)\) diz que os valores de saída de\(g\) são metade dos valores de saída de\(f\) com as mesmas entradas. Por exemplo, sabemos disso\(f(4)=3\). Então
\[g(4)=\frac{1}{2}f(4)=\frac{1}{2}(3)=\frac{3}{2} \nonumber\]
Fazemos o mesmo com os outros valores para produzir a Tabela\(\PageIndex{13}\).
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(g(x)\) | \(\dfrac{1}{2}\) | \(\dfrac{3}{2}\) | \(\dfrac{7}{2}\) | \(\dfrac{11}{2}\) |
Análise
O resultado é que a função\(g(x)\) foi comprimida verticalmente por\(\frac{1}{2}\). Cada valor de saída é dividido ao meio, então o gráfico tem metade da altura original.
Exercício\(\PageIndex{9}\)
Uma função\(f\) é fornecida como Tabela\(\PageIndex{14}\). Crie uma tabela para a função\(g(x)=\frac{3}{4}f(x)\).
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(f(x)\) | 12 | 16 | 20 | 0 |
- Resposta
-
Tabela\(\PageIndex{15}\) \(x\) 2 4 6 8 \(g(x)\) 9 12 15 0
Exemplo\(\PageIndex{16}\): Recognizing a Vertical Stretch
O gráfico na Figura\(\PageIndex{26}\) é uma transformação da função do kit de ferramentas\(f(x)=x^3\). Relacione essa nova função\(g(x)\) com e\(f(x)\), em seguida, encontre uma fórmula para\(g(x)\).
Ao tentar determinar um alongamento ou desvio vertical, é útil procurar um ponto no gráfico que seja relativamente claro. Neste gráfico, parece que\(g(2)=2\). Com a função cúbica básica na mesma entrada,\(f(2)=2^3=8\). Com base nisso, parece que as saídas de\(g\) são\(\frac{1}{4}\) as saídas da função\(f\) porque\(g(2)=\frac{1}{4}f(2)\). A partir disso, podemos concluir isso com bastante segurança\(g(x)=\frac{1}{4}f(x)\).
Podemos escrever uma fórmula para\(g\) usando a definição da função\(f\).
\[g(x)=\frac{1}{4} f(x)=\frac{1}{4}x^3.\]
Exercício\(\PageIndex{1}\)
Escreva a fórmula para a função que obtemos quando ampliamos a função do kit de ferramentas de identidade em um fator de 3 e, em seguida, diminua-a em 2 unidades.
- Resposta
-
\(g(x)=3x-2\)
Alongamentos e compressões horizontais
Agora vamos considerar as mudanças no interior de uma função. Quando multiplicamos a entrada de uma função por uma constante positiva, obtemos uma função cujo gráfico é esticado ou comprimido horizontalmente em relação ao gráfico da função original. Se a constante estiver entre 0 e 1, obtemos um alongamento horizontal; se a constante for maior que 1, obtemos uma compressão horizontal da função.
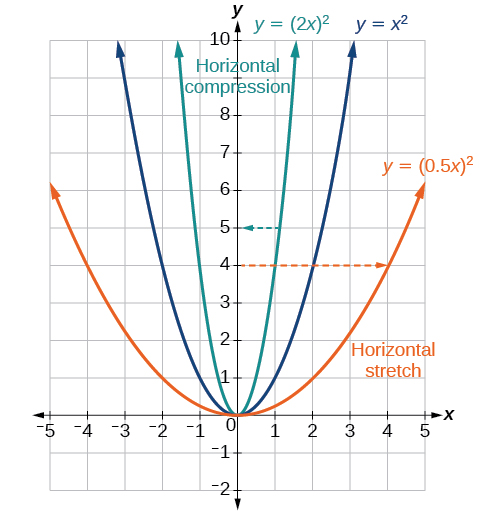
Dada uma função\(y=f(x)\), o formulário\(y=f(bx)\) resulta em um alongamento ou compressão horizontal. Considere a função\(y=x^2\). Observe a figura\(\PageIndex{27}\). O gráfico de\(y=(0.5x)^2\) é um trecho horizontal do gráfico da função\(y=x^2\) por um fator de 2. O gráfico de\(y=(2x)^2\) é uma compressão horizontal do gráfico da função\(y=x^2\) por um fator de 2.
Definições: alongamentos e compressões horizontais
Dada uma função\(f(x)\), uma nova função\(g(x)=f(bx)\), onde\(b\) é uma constante, é um alongamento horizontal ou compressão horizontal da função\(f(x)\).
- Se\(b>1\) sim, então o gráfico será compactado por\(\frac{1}{b}\).
- Se\(0<b<1\) sim, então o gráfico será esticado por\(\frac{1}{b}\).
- Se\(b<0\), então, haverá uma combinação de um estiramento ou compressão horizontal com uma reflexão horizontal.
Como...
Dada a descrição de uma função, desenhe uma compressão ou estiramento horizontal.
- Escreva uma fórmula para representar a função.
- Defina\(g(x)=f(bx)\) onde\(b>1\) para uma compressão ou\(0<b<1\) para um alongamento.
Exemplo\(\PageIndex{17}\): Graphing a Horizontal Compression
Suponha que um cientista esteja comparando uma população de moscas-das-frutas com uma população que progride ao longo de sua vida útil duas vezes mais rápido que a população original. Em outras palavras, essa nova população,\(R\), progredirá em 1 hora na mesma quantidade que a população original em 2 horas e, em 2 horas, progredirá tanto quanto a população original em 4 horas. Esboce um gráfico dessa população.
Solução
Simbolicamente, poderíamos escrever
\(\begin{align} R(1)&=P(2), \\ R(2)&=P(4), &\text{and in general,} \\ R(t)&=P(2t).\end{align}\)
Veja a Figura\(\PageIndex{28}\) para uma comparação gráfica da população original e da população comprimida.
![Dois gráficos lado a lado. O primeiro gráfico tem função para a população original cujo domínio é [0,7] e alcance é [0,3]. O valor máximo ocorre em (3,3). O segundo gráfico tem a mesma forma do primeiro, exceto que tem metade da largura. É um gráfico da população transformada, com um domínio de [0, 3,5] e um intervalo de [0,3]. O máximo ocorre em (1,5, 3).](https://math.libretexts.org/@api/deki/files/995/CNX_Precalc_Figure_01_05_029ab.jpg)
Análise
Observe que o efeito no gráfico é uma compressão horizontal em que todos os valores de entrada são metade da distância original do eixo vertical.
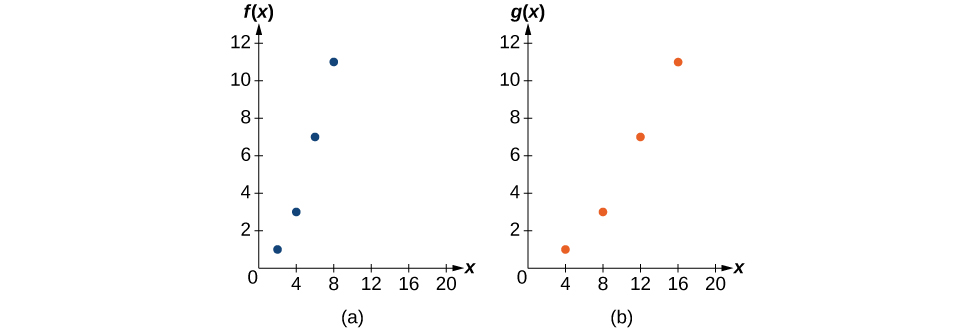
Exemplo\(\PageIndex{18}\): Finding a Horizontal Stretch for a Tabular Function
Uma função\(f(x)\) é fornecida como Tabela\(\PageIndex{16}\). Crie uma tabela para a função\(g(x)=f(\frac{1}{2}x)\).
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(f(x)\) | 1 | 3 | 7 | 11 |
A fórmula nos\(g(x)=f(\frac{1}{2}x)\) diz que os valores de saída para\(g\) são iguais aos valores de saída para a função\(f\) em uma entrada com metade do tamanho. Observe que não temos informações suficientes para determinar\(g(2)\) porque\(g(2)=f(\frac{1}{2}⋅2)=f(1)\), e não temos um valor para\(f(1)\) em nossa tabela. Nossos valores de entrada para\(g\) precisarão ser duas vezes maiores para obter entradas\(f\) que possamos avaliar. Por exemplo, podemos determinar\(g(4)\).
\[g(4)=f(\dfrac{1}{2}⋅4)=f(2)=1\]
Fazemos o mesmo com os outros valores para produzir a Tabela\(\PageIndex{17}\).
| \(x\) | 4 | 8 | 12 | 16 |
|---|---|---|---|---|
| \(g(x)\) | 1 | 3 | 7 | 11 |
A figura\(\PageIndex{29}\) mostra os gráficos de ambos os conjuntos de pontos.
Análise
Como cada valor de entrada foi dobrado, o resultado é que a função\(g(x)\) foi esticada horizontalmente por um fator de 2.
Exemplo\(\PageIndex{19}\): Recognizing a Horizontal Compression on a Graph
Relacione\(g(x)\) a função com a\(f(x)\) Figura\(\PageIndex{30}\).
Solução
O gráfico de\(g(x)\) se parece com o gráfico de comprimido\(f(x)\) horizontalmente. Como\(f(x)\) termina em (6,4) e\(g(x)\) termina em (2,4), podemos ver que os valores de x foram comprimidos por\(\frac{1}{3}\), porque\(6(\frac{1}{3})=2\). Também podemos notar que\(g(2)=f(6)\)\(g(1)=f(3)\) e. De qualquer jeito, podemos descrever esse relacionamento como\(g(x)=f(3x)\). Esta é uma compressão horizontal de\(\frac{1}{3}\).
Análise
Observe que o coeficiente necessário para um alongamento ou compressão horizontal é o inverso do alongamento ou compressão. Então, para esticar o gráfico horizontalmente por um fator de escala de 4, precisamos de um coeficiente de\(\frac{1}{4}\) em nossa função:\(f(\frac{1}{4}x)\). Isso significa que os valores de entrada devem ser quatro vezes maiores para produzir o mesmo resultado, exigindo que a entrada seja maior, causando o alongamento horizontal.
Exercício\(\PageIndex{11}\)
Escreva uma fórmula para a função de raiz quadrada do kit de ferramentas esticada horizontalmente por um fator de 3.
- Resposta
-
\(g(x)=f(\frac{1}{3}x)\), então, usando a função de raiz quadrada, obtemos\(g(x)=\sqrt{\frac{1}{3}x}\)
Executando uma sequência de transformações
Ao combinar transformações, é muito importante considerar a ordem das transformações. Por exemplo, deslocar verticalmente em 3 e depois esticar verticalmente em 2 não cria o mesmo gráfico que esticar verticalmente por 2 e depois deslocar verticalmente por 3, porque quando mudamos primeiro, tanto a função original quanto a mudança são esticadas, enquanto somente a função original é esticada quando estique primeiro.
Quando vemos uma expressão como\(2f(x)+3\), com qual transformação devemos começar? A resposta aqui segue muito bem a ordem das operações. Dado o valor de saída de\(f(x)\), primeiro multiplicamos por 2, causando o alongamento vertical, e depois adicionamos 3, causando a mudança vertical. Em outras palavras, multiplicação antes da adição.
É um pouco mais difícil pensar em transformações horizontais. Quando escrevemos\(g(x)=f(2x+3)\), por exemplo, temos que pensar em como as entradas da função\(g\) se relacionam com as entradas da função\(f\). Suponha que sabemos\(f(7)=12\). Qual entrada\(g\) produziria essa saída? Em outras palavras, que valor\(x\) permitiria\(g(x)=f(2x+3)=12?\) Nós precisaríamos\(2x+3=7\). Para resolver\(x\), primeiro subtrairíamos 3, resultando em uma mudança horizontal, e depois dividiríamos por 2, causando uma compressão horizontal.
Esse formato acaba sendo muito difícil de trabalhar, pois geralmente é muito mais fácil esticar horizontalmente um gráfico antes de deslocá-lo. Podemos contornar isso fatorando dentro da função.
\[f(bx+p)=f(b(x+\frac{p}{b})) \nonumber\]
Vamos analisar um exemplo.
\[f(x)=(2x+4)^2 \nonumber\]
Podemos considerar um 2.
\[f(x)=(2(x+2))^2 \nonumber\]
Agora podemos observar com mais clareza um deslocamento horizontal para a esquerda de 2 unidades e uma compressão horizontal. A fatoração dessa maneira nos permite esticar horizontalmente primeiro e depois mudar horizontalmente.
Combinando transformações
- Ao combinar transformações verticais escritas no formulário\(af(x)+k\), primeiro estique verticalmente\(a\) e depois mude verticalmente\(k\).
- Ao combinar transformações horizontais escritas no formulário\(f(bx+h)\), primeiro mude horizontalmente\(h\) e depois alongue horizontalmente\(\frac{1}{b}\).
- Ao combinar transformações horizontais escritas no formulário\(f(b(x+h))\), primeiro estique horizontalmente\(\frac{1}{b}\) e depois mude horizontalmente\(h\).
- As transformações horizontais e verticais são independentes. Não importa se as transformações horizontais ou verticais são realizadas primeiro.
Exemplo\(\PageIndex{20}\): Finding a Triple Transformation of a Tabular Function
Dada a Tabela\(\PageIndex{18}\) para a função\(f(x)\), crie uma tabela de valores para a função\(g(x)=2f(3x)+1\).
| \(x\) | 6 | 12 | 18 | 24 |
|---|---|---|---|---|
| \(f(x)\) | 10 | 14 | 15 | 17 |
Solução
Há três etapas para essa transformação e trabalharemos de dentro para fora. Começando com as transformações horizontais,\(f(3x)\) é uma compressão horizontal por\(\frac{1}{3}\), o que significa que multiplicamos cada\(x\) valor -por\(\frac{1}{3}\) .Veja a tabela\(\PageIndex{19}\).
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(f(3x)\) | 10 | 14 | 15 | 17 |
Olhando agora para as transformações verticais, começamos com o alongamento vertical, que multiplicará os valores de saída por 2. Nós aplicamos isso à transformação anterior. Veja a tabela\(\PageIndex{20}\).
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(2f(3x)\) | 20 | 28 | 30 | 34 |
Finalmente, podemos aplicar o deslocamento vertical, que adicionará 1 a todos os valores de saída. Veja a tabela\(\PageIndex{21}\).
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(g(x)=2f(3x)+1+1\) | 21 | 29 | 31 | 35 |
Exemplo\(\PageIndex{21}\): Finding a Triple Transformation of a Graph
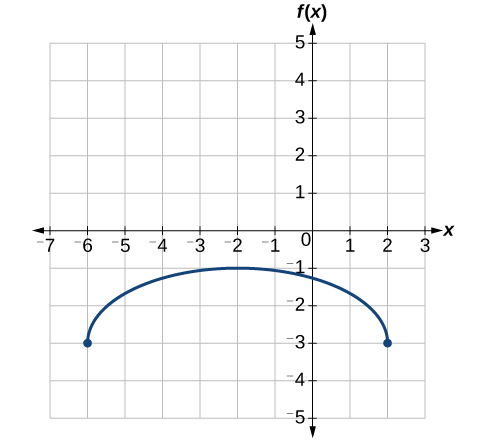
Use o gráfico de\(f(x)\) na Figura\(\PageIndex{31}\) para esboçar um gráfico de\(k(x)=f\Big(\frac{1}{2}x+1\Big)−3\).
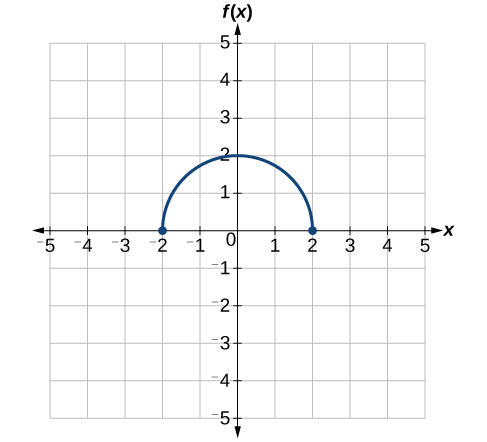
Para simplificar, vamos começar considerando o interior da função.
\[f\Big(\dfrac{1}{2}x+1\Big)−3=f\Big(\dfrac{1}{2}(x+2)\Big)−3\]
Ao fatorar o interior, podemos primeiro esticar horizontalmente\(\frac{1}{2}\) em 2, conforme indicado pela parte interna da função. Lembre-se de que duas vezes o tamanho de 0 ainda é 0, então o ponto\((0,2)\) permanece em até\((0,2)\) onde o ponto se\((2,0)\) estenderá\((4,0)\). Veja a Figura\(\PageIndex{32}\).
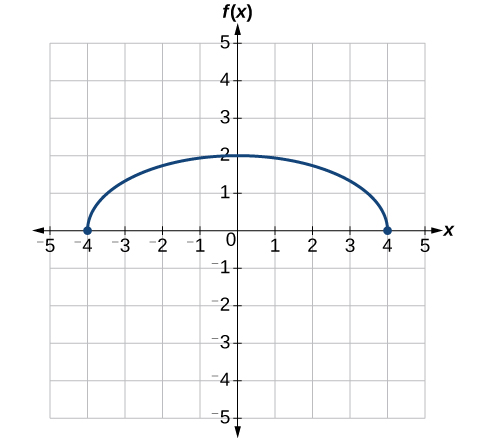
Em seguida, deslocamos horizontalmente para a esquerda em 2 unidades, conforme indicado por\(x+2\). Veja a Figura\(\PageIndex{33}\).
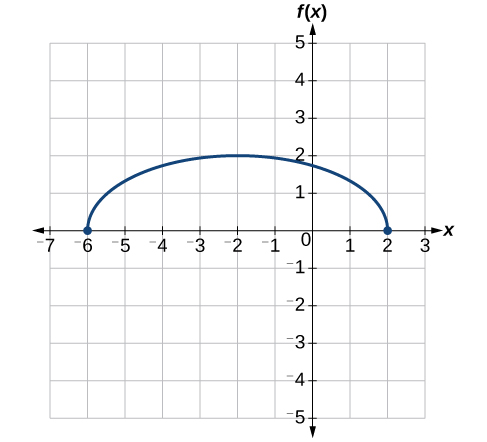
Por último, diminuímos verticalmente em 3 para completar nosso esboço, conforme indicado pelo −3 na parte externa da função. Veja a Figura\(\PageIndex{34}\).
Equações-chave
- Deslocamento vertical\(g(x)=f(x)+k\) (para cima\(k>0\))
- Deslocamento horizontal\(g(x)=f(x−h)\) (à direita) para\(h>0\)
- Reflexão vertical\(g(x)=−f(x)\)
- Reflexão horizontal\(g(x)=f(−x)\)
- Estiramento vertical\(g(x)=af(x)\) (a>0)
- Compressão vertical\(g(x)=af(x)\) (0<a<1)
- Estiramento horizontal\(g(x)=f(bx)(0<b<1)\)
- Compressão horizontal\(g(x)=f(bx)\) (b>1)
Conceitos-chave
- Uma função pode ser deslocada verticalmente adicionando uma constante à saída.
- Uma função pode ser deslocada horizontalmente adicionando uma constante à entrada.
- Relacionar a mudança ao contexto de um problema possibilita comparar e interpretar mudanças verticais e horizontais.
- As mudanças verticais e horizontais geralmente são combinadas.
- Uma reflexão vertical reflete um gráfico sobre o eixo x. Um gráfico pode ser refletido verticalmente multiplicando a saída por —1.
- Uma reflexão horizontal reflete um gráfico sobre o eixo y. Um gráfico pode ser refletido horizontalmente multiplicando a entrada por —1.
- Um gráfico pode ser refletido tanto na vertical quanto na horizontal. A ordem na qual as reflexões são aplicadas não afeta o gráfico final.
- Uma função apresentada em forma de tabela também pode ser refletida multiplicando-se os valores nas linhas ou colunas de entrada e saída de forma adequada.
- Uma função apresentada como uma equação pode ser refletida aplicando transformações uma de cada vez.
- As funções pares são simétricas em relação ao eixo y, enquanto as funções ímpares são simétricas em relação à origem.
- Até mesmo as funções satisfazem a condição\(f(x)=f(−x)\).
- Funções estranhas satisfazem a condição\(f(x)=−f(−x)\).
- Uma função pode ser ímpar, par ou nenhuma delas.
- Uma função pode ser comprimida ou esticada verticalmente multiplicando a saída por uma constante.
- Uma função pode ser comprimida ou esticada horizontalmente multiplicando a entrada por uma constante.
- A ordem na qual diferentes transformações são aplicadas afeta a função final. As transformações verticais e horizontais devem ser aplicadas na ordem indicada. No entanto, uma transformação vertical pode ser combinada com uma transformação horizontal em qualquer ordem.
Glossário
função uniforme
uma função cujo gráfico é inalterado pela reflexão horizontal,\(f(x)=f(−x)\), e é simétrico em relação ao eixo y
compressão horizontal:
uma transformação que comprime o gráfico de uma função horizontalmente, multiplicando a entrada por uma constante b>1
reflexão horizontal:
uma transformação que reflete o gráfico de uma função no eixo y multiplicando a entrada por −1.
deslocamento horizontal -
uma transformação que desloca o gráfico de uma função para a esquerda ou para a direita adicionando uma constante positiva ou negativa à entrada.
estiramento horizontal:
uma transformação que estica o gráfico de uma função horizontalmente multiplicando a entrada por uma constante 0<b<1
função ímpar:
uma função cujo gráfico é inalterado pela reflexão horizontal e vertical combinada\(f(x)=−f(−x)\), e é simétrico quanto à origem
compressão vertical
uma transformação de função que comprime o gráfico da função verticalmente multiplicando a saída por uma constante 0<a<1
reflexão vertical:
uma transformação que reflete o gráfico de uma função no eixo x multiplicando a saída por −1.
deslocamento vertical -
uma transformação que desloca o gráfico de uma função para cima ou para baixo adicionando uma constante positiva ou negativa à saída.
estiramento vertical
uma transformação que estica o gráfico de uma função verticalmente multiplicando a saída por uma constante a>1


