3.3: Domínio e alcance
- Page ID
- 189400
Objetivos de
- Encontre o domínio de uma função definida por uma equação.
- Represente graficamente funções definidas por partes.
Se você está com vontade de assistir a um filme de terror, talvez queira conferir um dos cinco filmes de terror mais populares de todos os tempos: I am Legend, Hannibal, The Ring, The Grudge e The Conjuring. A figura\(\PageIndex{1}\) mostra a quantia, em dólares, que cada um desses filmes arrecadou quando foram lançados, bem como a venda de ingressos para filmes de terror em geral por ano. Observe que podemos usar os dados para criar uma função da quantidade que cada filme ganhou ou do total de vendas de ingressos para todos os filmes de terror por ano. Ao criar várias funções usando os dados, podemos identificar diferentes variáveis independentes e dependentes e analisar os dados e as funções para determinar o domínio e o intervalo. Nesta seção, investigaremos métodos para determinar o domínio e a variedade de funções como essas.
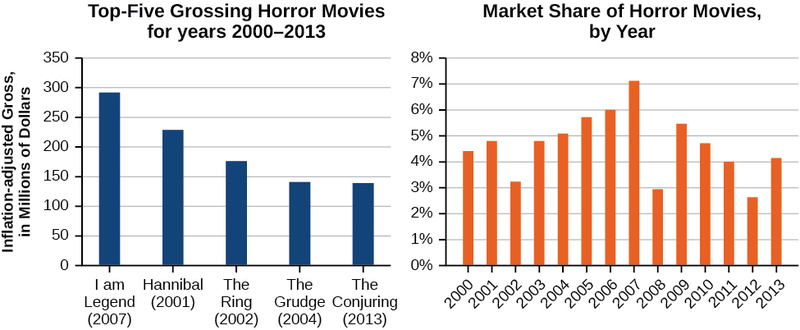
Encontrando o domínio de uma função definida por uma equação
Em Funções e Notação de Função, fomos apresentados aos conceitos de domínio e alcance. Nesta seção, praticaremos a determinação de domínios e intervalos para funções específicas. Lembre-se de que, ao determinar domínios e intervalos, precisamos considerar o que é fisicamente possível ou significativo em exemplos do mundo real, como a venda de ingressos e o ano no exemplo do filme de terror acima. Também precisamos considerar o que é matematicamente permitido. Por exemplo, não podemos incluir nenhum valor de entrada que nos leve a obter uma raiz par de um número negativo se o domínio e o intervalo consistirem em números reais. Ou, em uma função expressa como uma fórmula, não podemos incluir nenhum valor de entrada no domínio que nos leve a dividir por 0.
Podemos visualizar o domínio como uma “área de retenção” que contém “matérias-primas” para uma “máquina funcional” e o alcance como outra “área de retenção” para os produtos da máquina (Figura\(\PageIndex{2}\)).
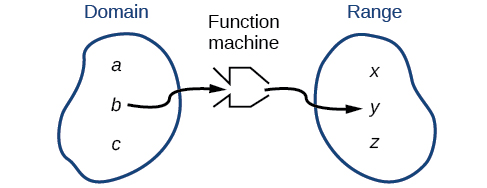
Podemos escrever o domínio e o intervalo em notação de intervalo, que usa valores entre colchetes para descrever um conjunto de números. Na notação de intervalo, usamos um colchete [quando o conjunto inclui o ponto final e um parêntese (para indicar que o ponto final não está incluído ou o intervalo é ilimitado). Por exemplo, se uma pessoa tiver $100 para gastar, ela precisaria expressar o intervalo maior que 0 e menor ou igual a 100 e escrever\(\left(0, 100\right]\). Discutiremos a notação de intervalo com mais detalhes posteriormente.
Vamos voltar nossa atenção para encontrar o domínio de uma função cuja equação é fornecida. Muitas vezes, encontrar o domínio de tais funções envolve lembrar três formas diferentes. Primeiro, se a função não tiver um denominador ou uma raiz par, considere se o domínio pode ser todo números reais. Segundo, se houver um denominador na equação da função, exclua valores no domínio que forçam o denominador a ser zero. Terceiro, se houver uma raiz uniforme, considere excluir valores que tornariam o radical e negativo.
Antes de começarmos, vamos revisar as convenções da notação de intervalo:
- O menor termo do intervalo é escrito primeiro.
- O maior termo no intervalo é escrito em segundo lugar, após uma vírgula.
- Parênteses,\((\) ou\()\), são usados para indicar que um endpoint não está incluído, chamado exclusivo.
- Os colchetes\(]\),\([\) ou, são usados para indicar que um ponto final está incluído, chamado inclusivo.
Consulte a Figura\(\PageIndex{3}\) para obter um resumo da notação de intervalo.
Exemplo\(\PageIndex{1}\): Finding the Domain of a Function as a Set of Ordered Pairs
Encontre o domínio da seguinte função:\(\{(2, 10),(3, 10),(4, 20),(5, 30),(6, 40)\}\).
Solução
Primeiro identifique os valores de entrada. O valor de entrada é a primeira coordenada em um par ordenado. Não há restrições, pois os pares pedidos são simplesmente listados. O domínio é o conjunto das primeiras coordenadas dos pares ordenados.
\[\{2,3,4,5,6\} \nonumber\]
Exercício\(\PageIndex{1}\)
Encontre o domínio da função:
\[\{(−5,4),(0,0),(5,−4),(10,−8),(15,−12)\} \nonumber\]
- Responda
-
\(\{−5, 0, 5, 10, 15\}\)
Como fazer: Dada uma função escrita em forma de equação, encontre o domínio.
- Identifique os valores de entrada.
- Identifique quaisquer restrições na entrada e exclua esses valores do domínio.
- Escreva o domínio em forma de intervalo, se possível.
Exemplo\(\PageIndex{2}\): Finding the Domain of a Function
Encontre o domínio da função\(f(x)=x^2−1\).
Solução
O valor de entrada, mostrado pela variável x na equação, é quadrado e, em seguida, o resultado é reduzido em um. Qualquer número real pode ser quadrado e depois reduzido em um, portanto, não há restrições no domínio dessa função. O domínio é o conjunto de números reais.
Na forma de intervalo, o domínio de f é\((−\infty,\infty)\).
Exercício\(\PageIndex{2}\)
Encontre o domínio da função:
\[f(x)=5−x+x^3 \nonumber\]
- Responda
-
\((−\infty,\infty)\)
Como fazer: Dada uma função escrita em forma de equação que inclui uma fração, encontre o domínio
- Identifique os valores de entrada.
- Identifique quaisquer restrições na entrada. Se houver um denominador na fórmula da função, defina o denominador igual a zero e resolva x. Se a fórmula da função contiver uma raiz par, defina o radicando maior ou igual a 0 e resolva.
- Escreva o domínio em formato de intervalo, certificando-se de excluir quaisquer valores restritos do domínio.
Exemplo\(\PageIndex{3}\): Finding the Domain of a Function Involving a Denominator
Encontre o domínio da função\(f(x)=\dfrac{x+1}{2−x}\).
Solução
Quando há um denominador, queremos incluir somente valores da entrada que não forçam o denominador a ser zero. Então, definiremos o denominador igual a 0 e resolveremos por x.
\[ \begin{align*} 2−x=0 \\[4pt] −x &=−2 \\[4pt] x&=2 \end{align*}\]
Agora, excluiremos 2 do domínio. As respostas são todas números reais onde\(x<2\) ou\(x>2\). Podemos usar um símbolo conhecido como união,\(\cup\), para combinar os dois conjuntos. Na notação de intervalo, escrevemos a solução:\((−\infty,2)∪(2,\infty)\).
![[Gráfico de linha de f (x).]](https://math.libretexts.org/@api/deki/files/893/CNX_Precalc_Figure_01_02_028n.jpg)
Na forma de intervalo, o domínio de f é\((−\infty,2)\cup(2,\infty)\).
Exercício\(\PageIndex{3}\)
Encontre o domínio da função:
\[f(x)=\dfrac{1+4x}{2x−1} \nonumber\]
- Responda
-
\[(−\infty,\dfrac{1}{2})\cup(\dfrac{1}{2},\infty) \nonumber\]
Como fazer: Dada uma função escrita em forma de equação, incluindo uma raiz par, encontre o domínio.
- Identifique os valores de entrada.
- Como existe uma raiz par, exclua qualquer número real que resulte em um número negativo no radicando. Defina o radicando maior ou igual a zero e resolva x.
- A (s) solução (s) são o domínio da função. Se possível, escreva a resposta em forma de intervalo.
Exemplo\(\PageIndex{4}\): Finding the Domain of a Function with an Even Root
Encontre o domínio da função:
\[f(x)=\sqrt{7-x} \nonumber .\]
Solução
Quando há uma raiz par na fórmula, excluímos qualquer número real que resulte em um número negativo no radicando.
Defina o radicando maior ou igual a zero e resolva x.
\[ \begin{align*} 7−x&≥0 \\[4pt] −x&≥−7\\[4pt] x&≤7 \end{align*}\]
Agora, excluiremos qualquer número maior que 7 do domínio. As respostas são todas números reais menores ou iguais a 7, ou\(\left(−\infty,7\right]\).
Exercício\(\PageIndex{4}\)
Encontre o domínio da função
\[f(x)=\sqrt{5+2x}. \nonumber\]
- Responda
-
\[\left[−2.5,\infty\right) \nonumber\]
Perguntas e respostas: Pode haver funções nas quais o domínio e o intervalo não se cruzam?
Sim. Por exemplo, a função\(f(x)=-\dfrac{1}{\sqrt{x}}\) tem o conjunto de todos os números reais positivos como seu domínio, mas o conjunto de todos os números reais negativos como seu intervalo. Como um exemplo mais extremo, as entradas e saídas de uma função podem ser categorias completamente diferentes (por exemplo, nomes de dias da semana como entradas e números como saídas, como em um gráfico de presença). Nesses casos, o domínio e o intervalo não têm elementos em comum.
Usando notações para especificar domínio e intervalo
Nos exemplos anteriores, usamos desigualdades e listas para descrever o domínio das funções. Também podemos usar desigualdades ou outras declarações que possam definir conjuntos de valores ou dados para descrever o comportamento da variável na notação do construtor de conjuntos. Por exemplo,\(\{x|10≤x<30\}\) descreve o comportamento de x na notação do construtor de conjuntos. Os colchetes\(\{\}\) são lidos como “o conjunto de” e a barra vertical\(|\) é lida como “tal que”, então leríamos\( \{x|10≤x<30\}\) como “o conjunto de valores x de forma que 10 seja menor ou igual a x e x seja menor que 30”.
A figura\(\PageIndex{4}\) compara a notação de desigualdade, a notação do construtor de conjuntos e a notação de intervalo.
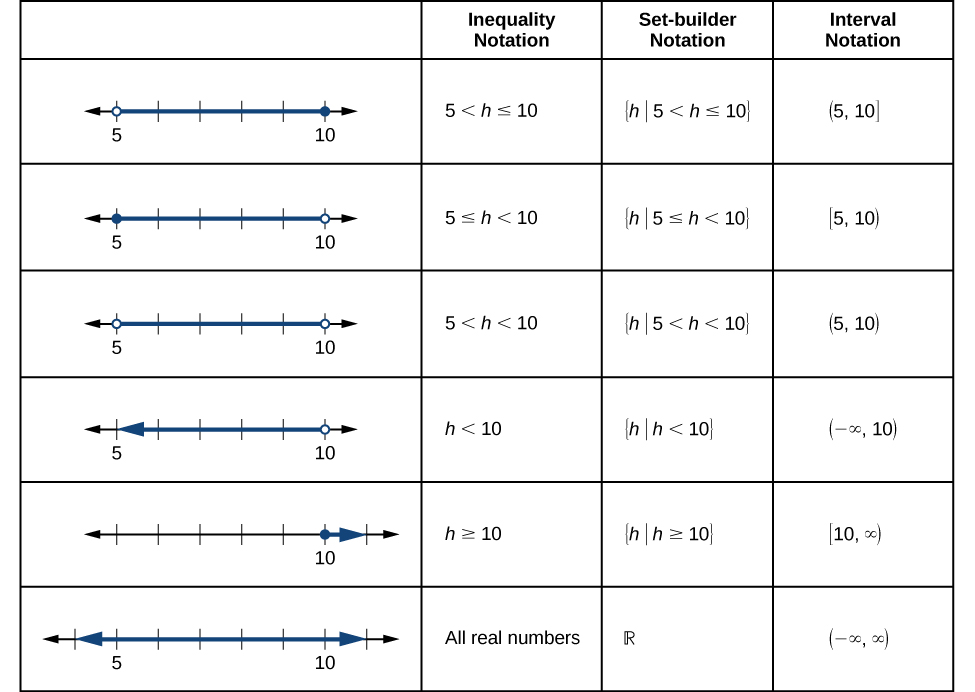
Para combinar dois intervalos usando notação de desigualdade ou notação de construtor de conjuntos, usamos a palavra “ou”. Como vimos em exemplos anteriores, usamos o símbolo de união,\(\cup\), para combinar dois intervalos não conectados. Por exemplo, a união dos conjuntos\(\{2,3,5\}\) e\(\{4,6\}\) é o conjunto\(\{2,3,4,5,6\}\). É o conjunto de todos os elementos que pertencem a um ou outro (ou ambos) dos dois conjuntos originais. Para conjuntos com um número finito de elementos como esses, os elementos não precisam ser listados em ordem crescente de valor numérico. Se os dois conjuntos originais tiverem alguns elementos em comum, esses elementos devem ser listados somente uma vez no conjunto de uniões. Para conjuntos de números reais em intervalos, outro exemplo de união é
\[\{x| |x|≥3\}=\left(−\infty,−3\right]\cup\left[3,\infty\right)\]
Notação Set-Builder e notação de intervalo
A notação de construtor de conjuntos é um método de especificar um conjunto de elementos que satisfazem uma determinada condição. Ele assume a forma\(\{x|\text{ statement about x}\}\) que é lida como “o conjunto de todos os x de forma que a afirmação sobre x seja verdadeira”. Por exemplo,
\[\{x|4<x≤12\} \nonumber\]
A notação de intervalo é uma forma de descrever conjuntos que incluem todos os números reais entre um limite inferior que pode ou não ser incluído e um limite superior que pode ou não ser incluído. Os valores do ponto final estão listados entre colchetes ou parênteses. Um colchete indica inclusão no conjunto e um parêntese indica exclusão do conjunto. Por exemplo,
\[\left(4,12\right] \nonumber\]
![]() Dado um gráfico de linhas, descreva o conjunto de valores usando a notação de intervalo.
Dado um gráfico de linhas, descreva o conjunto de valores usando a notação de intervalo.
- Identifique os intervalos a serem incluídos no conjunto determinando onde a linha pesada se sobrepõe à linha real.
- No final esquerdo de cada intervalo, use [com cada valor final a ser incluído no conjunto (ponto sólido) ou (para cada valor final excluído (ponto aberto).
- Na extremidade direita de cada intervalo, use] com cada valor final a ser incluído no conjunto (ponto preenchido) ou) para cada valor final excluído (ponto aberto).
- Use o símbolo da união\(\cup\) para combinar todos os intervalos em um conjunto.
Exemplo\(\PageIndex{5}\): Describing Sets on the Real-Number Line
Descreva os intervalos dos valores mostrados na Figura\(\PageIndex{5}\) usando notação de desigualdade, notação de construtor de conjuntos e notação de intervalo.
Solução
Para descrever os valores\(x\), incluídos nos intervalos mostrados, diríamos que “\(x\)é um número real maior ou igual a 1 e menor ou igual a 3, ou um número real maior que 5”.
Desigualdade
\[1≤x≤3 \text{ or }x>5 \nonumber\]
Notação Set-Builder
\[\{x|1≤x≤3 \text{ or } x>5\}\nonumber\]
Notação de intervalo
\[[1,3]\cup(5,\infty)\nonumber\]
Lembre-se de que, ao escrever ou ler a notação de intervalo, usar um colchete significa que o limite está incluído no conjunto. Usar um parêntese significa que o limite não está incluído no conjunto.
Exercício\(\PageIndex{5}\)
Figura fornecida\(\PageIndex{6}\), especifique o conjunto representado graficamente em
- palavras
- notação de construtor de conjuntos
- notação de intervalo
![[Gráfico de linha de -2<=x, -1<=x<3.]](https://math.libretexts.org/@api/deki/files/877/CNX_Precalc_Figure_01_02_005.jpg)
- Responda a
-
Valores menores ou iguais a —2, ou valores maiores ou iguais a —1 e menores que 3;
- Resposta b
-
\(\{x|x≤−2 or −1≤x<3\}\)
- Resposta c
-
\(\left(−∞,−2\right]\cup\left[−1,3\right)\)
Encontrando domínio e intervalo a partir de gráficos
Outra forma de identificar o domínio e a variedade de funções é usando gráficos. Como o domínio se refere ao conjunto de possíveis valores de entrada, o domínio de um gráfico consiste em todos os valores de entrada mostrados no eixo x. O intervalo é o conjunto de possíveis valores de saída, que são mostrados no eixo y. Lembre-se de que, se o gráfico continuar além da parte do gráfico que podemos ver, o domínio e o intervalo podem ser maiores do que os valores visíveis. Veja a Figura\(\PageIndex{7}\).
![[Gráfico de um polinômio que mostra que o eixo x é o domínio e o eixo y é o intervalo]](https://math.libretexts.org/@api/deki/files/878/CNX_Precalc_Figure_01_02_006.jpg)
Podemos observar que o gráfico se estende horizontalmente de −5 para a direita sem limite, então o domínio é\(\left[−5,∞\right)\). A extensão vertical do gráfico é de todos os valores do intervalo 5 e abaixo, então o intervalo é\(\left(−∞,5\right]\). Observe que o domínio e o intervalo são sempre escritos de valores menores para maiores, ou da esquerda para a direita para o domínio e da parte inferior do gráfico até a parte superior do gráfico para o intervalo.
Exemplo\(\PageIndex{6A}\): Finding Domain and Range from a Graph
Encontre o domínio e o alcance da função f cujo gráfico é mostrado na Figura 1.2.8.
![[Gráfico de uma função de (-3, 1].]](https://math.libretexts.org/@api/deki/files/879/CNX_Precalc_Figure_01_02_007.jpg)
Solução
Podemos observar que a extensão horizontal do gráfico é de —3 a 1, então o domínio de f é\(\left(−3,1\right]\).
A extensão vertical do gráfico é de 0 a —4, então o intervalo é\(\left[−4,0\right)\). Veja a Figura\(\PageIndex{9}\).
![[O gráfico da função anterior mostra o domínio e o intervalo.]](https://math.libretexts.org/@api/deki/files/880/CNX_Precalc_Figure_01_02_008.jpg)
Exemplo\(\PageIndex{6B}\): Finding Domain and Range from a Graph of Oil Production
Encontre o domínio e o alcance da função f cujo gráfico é mostrado na Figura\(\PageIndex{10}\).
![[Gráfico da produção de petróleo bruto do Alasca, onde o eixo y é de mil barris por dia e o eixo -são os anos.]](https://math.libretexts.org/@api/deki/files/881/CNX_Precalc_Figure_01_02_009.jpg)
Solução
A quantidade de entrada ao longo do eixo horizontal é “anos”, que representamos com a variável t para o tempo. A quantidade produzida é “milhares de barris de petróleo por dia”, que representamos com a variável b para barris. O gráfico pode continuar à esquerda e à direita além do que é visualizado, mas com base na parte do gráfico que é visível, podemos determinar o domínio como\(1973≤t≤2008\) e o intervalo como aproximadamente\(180≤b≤2010\).
Na notação de intervalo, o domínio é\([1973, 2008]\) e o intervalo é de aproximadamente\([180, 2010]\). Para o domínio e o intervalo, aproximamos os menores e maiores valores, pois eles não caem exatamente nas linhas da grade.
Exercício\(\PageIndex{6}\)
Dada a Figura\(\PageIndex{11}\), identifique o domínio e o intervalo usando a notação de intervalo.
![[Gráfico do aumento da população mundial em que o eixo y representa milhões de pessoas e o eixo x representa o ano.]](https://math.libretexts.org/@api/deki/files/882/CNX_Precalc_Figure_01_02_010.jpg)
- Responda
-
domínio =\([1950,2002]\)
intervalo =\([47,000,000,89,000,000]\)
![]() O domínio e o alcance de uma função podem ser os mesmos?
O domínio e o alcance de uma função podem ser os mesmos?
Sim. Por exemplo, o domínio e o intervalo da função raiz cúbica são o conjunto de todos os números reais.
Encontrando domínios e intervalos das funções do kit de ferramentas
Agora retornaremos ao nosso conjunto de funções do kit de ferramentas para determinar o domínio e o alcance de cada uma.
![[Função constante f (x) =c.]](https://math.libretexts.org/@api/deki/files/883/CNX_Precalc_Figure_01_02_011.jpg)
Para a função constante\( f(x)=c\), o domínio consiste em todos os números reais; não há restrições na entrada. O único valor de saída é a constante\(c\), então o intervalo é o conjunto\(\{c\}\) que contém esse único elemento. Na notação de intervalo, isso é escrito como\([c,c]\) o intervalo que começa e termina com\(c\).
![[Função de identidade f (x) =x.]](https://math.libretexts.org/@api/deki/files/884/CNX_Precalc_Figure_01_02_012.jpg)
Figura\(\PageIndex{13}\): Função de identidade f (x) =x.
Para a função de identidade\(f(x)=x\), não há nenhuma restrição em\(x\). Tanto o domínio quanto o intervalo são o conjunto de todos os números reais.
![[Função absoluta f (x) =|x|.]](https://math.libretexts.org/@api/deki/files/885/CNX_Precalc_Figure_01_02_013.jpg)
Para a função de valor absoluto\(f(x)=|x|\), não há restrição em\(x\). No entanto, como o valor absoluto é definido como uma distância de 0, a saída só pode ser maior ou igual a 0.
![[função quadrática f (x) =x^2]](https://math.libretexts.org/@api/deki/files/886/CNX_Precalc_Figure_01_02_014.jpg)
Para a função quadrática\(f(x)=x^2\), o domínio é todo número real, já que a extensão horizontal do gráfico é toda a reta numérica real. Como o gráfico não inclui nenhum valor negativo para o intervalo, o intervalo é somente números reais não negativos.
![[Função cúbica f (x) -x^3.]](https://math.libretexts.org/@api/deki/files/887/CNX_Precalc_Figure_01_02_015.jpg)
Para a função cúbica\(f(x)=x^3\), o domínio é todo números reais porque a extensão horizontal do gráfico é toda a reta numérica real. O mesmo se aplica à extensão vertical do gráfico, portanto, o domínio e o intervalo incluem todos os números reais.
![[Função recíproca f (x) =1/x.]](https://math.libretexts.org/@api/deki/files/888/CNX_Precalc_Figure_01_02_016.jpg)
Para a função recíproca\(f(x)=\dfrac{1}{x}\), não podemos dividir por 0, então devemos excluir 0 do domínio. Além disso, 1 dividido por qualquer valor nunca pode ser 0, então o intervalo também não incluirá 0. Na notação do construtor de conjuntos, também poderíamos escrever\(\{x| x≠0\}\) o conjunto de todos os números reais que não são zero.
![[Função quadrada recíproca...]](https://math.libretexts.org/@api/deki/files/889/CNX_Precalc_Figure_01_02_017.jpg)
Para a função quadrada recíproca\(f(x)=\dfrac{1}{x^2}\), não podemos dividir por 0, então devemos excluir 0 do domínio. Também não há um x que possa fornecer uma saída de 0, então 0 também é excluído do intervalo. Observe que a saída dessa função é sempre positiva devido ao quadrado no denominador, portanto, o intervalo inclui somente números positivos.
![[Função de raiz quadrada f (x) =sqrt (x).]](https://math.libretexts.org/@api/deki/files/890/CNX_Precalc_Figure_01_02_018.jpg)
Figura\(\PageIndex{19}\): Função de raiz quadrada\(f(x)=\sqrt{(x)}\).
Para a função de raiz quadrada\(f(x)=\sqrt{x}\), não podemos usar a raiz quadrada de um número real negativo, então o domínio deve ser 0 ou maior. O intervalo também exclui números negativos porque a raiz quadrada de um número positivo\(x\) é definida como positiva, mesmo que o quadrado do número negativo\(−\sqrt{x}\) também nos forneça\(x\).
![[Função raiz cúbica f (x) =x^ (1/3).]](https://math.libretexts.org/@api/deki/files/891/CNX_Precalc_Figure_01_02_019.jpg)
Para a função raiz cúbica\(f(x)=\sqrt[3]{x}\), o domínio e o intervalo incluem todos os números reais. Observe que não há problema em obter uma raiz cúbica, ou qualquer raiz de número inteiro ímpar, de um número negativo, e a saída resultante é negativa (é uma função ímpar).
![]() Dada a fórmula de uma função, determine o domínio e o intervalo.
Dada a fórmula de uma função, determine o domínio e o intervalo.
- Exclua do domínio quaisquer valores de entrada que resultem na divisão por zero.
- Exclua do domínio quaisquer valores de entrada que tenham saídas numéricas não reais (ou indefinidas).
- Use os valores de entrada válidos para determinar o intervalo dos valores de saída.
- Examine o gráfico da função e os valores da tabela para confirmar o comportamento real da função.
Encontrando o domínio e o intervalo usando as funções do kit de ferramentas
Encontre o domínio e a variedade de\(f(x)=2x^3−x\).
Solução
Não há restrições no domínio, pois qualquer número real pode ser colocado ao cubo e depois subtraído do resultado.
O domínio é\((−\infty,\infty)\) e o intervalo também é\((−\infty,\infty)\).
Exemplo\(\PageIndex{7B}\): Finding the Domain and Range
Encontre o domínio e a variedade de\(f(x)=\frac{2}{x+1}\).
Solução
Não podemos avaliar a função em −1 porque a divisão por zero é indefinida. O domínio é\((−\infty,−1)\cup(−1,\infty)\). Como a função nunca é zero, excluímos 0 do intervalo. O alcance é\((−\infty,0)\cup(0,\infty)\).
Exemplo\(\PageIndex{7C}\): Finding the Domain and Range
Encontre o domínio e a variedade de\(f(x)=2 \sqrt{x+4}\).
Solução
Não podemos obter a raiz quadrada de um número negativo, então o valor dentro do radical não deve ser negativo.
\(x+4≥0\)quando\(x≥−4\)
O domínio de\(f(x)\) é\([−4,\infty)\).
Em seguida, encontramos o alcance. Sabemos\(f(−4)=0\) disso e o valor da função aumenta à medida que\(x\) aumenta, sem nenhum limite superior. Concluímos que o intervalo de f é\(\left[0,\infty\right)\).
Análise
A figura\(\PageIndex{19}\) representa a função\(f\).
 " src="https://math.libretexts.org/@api/dek..._01_02_020.jpg">
" src="https://math.libretexts.org/@api/dek..._01_02_020.jpg">
Exercício\(\PageIndex{7}\)
Encontre o domínio e a variedade de
\(f(x)=\sqrt{−2−x}\).
- Responda
-
domínio:\(\left(−\infty,-2\right]\)
alcance:\(\left[0,\infty\right)\)
Representação gráfica de funções definidas por partes
Às vezes, encontramos uma função que requer mais de uma fórmula para obter a saída dada. Por exemplo, nas funções do kit de ferramentas, introduzimos a função de valor absoluto\(f(x)=|x|\). Com um domínio de todos os números reais e uma faixa de valores maior ou igual a 0, o valor absoluto pode ser definido como a magnitude, ou módulo, de um valor de número real, independentemente do sinal. É a distância de 0 na reta numérica. Todas essas definições exigem que a saída seja maior ou igual a 0.
Se inserirmos 0, ou um valor positivo, a saída é a mesma da entrada.
\[ f(x)=x \; \text{ if } \; x≥0 \nonumber \]
Se inserirmos um valor negativo, a saída é o oposto da entrada.
\[ f(x) = -x \; \text { if } \; x < 0 \nonumber \]
Como isso requer dois processos ou partes diferentes, a função de valor absoluto é um exemplo de função por partes. Uma função por partes é uma função na qual mais de uma fórmula é usada para definir a saída em diferentes partes do domínio.
Usamos funções por partes para descrever situações em que uma regra ou relacionamento muda à medida que o valor de entrada cruza certos “limites”. Por exemplo, muitas vezes encontramos situações nos negócios em que o custo por peça de um determinado item é descontado quando o número pedido excede um determinado valor. Os escalões de impostos são outro exemplo real de funções por partes. Por exemplo, considere um sistema tributário simples no qual rendas de até $10.000 são tributadas em 10% e qualquer renda adicional é tributada em 20%. O imposto sobre a renda total S seria\(0.1S\) se\(S≤$10,000\) e\($1000+0.2(S−$10,000)\) se\(S>$10,000\).
Função por partes
Uma função por partes é uma função na qual mais de uma fórmula é usada para definir a saída. Cada fórmula tem seu próprio domínio, e o domínio da função é a união de todos esses domínios menores. Notamos essa ideia assim:
\[f(x)= \begin{cases} \text{formula 1} & \text{if x is in domain 1} \\ \text{formula 2} &\text{if x is in domain 2} \\ \text{formula 3} &\text{if x is in domain 3}\end{cases} \nonumber \]
Na notação por partes, a função de valor absoluto é
\[|x|= \begin{cases} x & \text{if $x \geq 0$} \\ -x &\text{if $x<0$} \end{cases} \nonumber \]
![]() Dada uma função por partes, escreva a fórmula e identifique o domínio para cada intervalo.
Dada uma função por partes, escreva a fórmula e identifique o domínio para cada intervalo.
- Identifique os intervalos aos quais regras diferentes se aplicam.
- Determine fórmulas que descrevem como calcular uma saída de uma entrada em cada intervalo.
- Use colchetes e declarações if para escrever a função.
Exemplo\(\PageIndex{8A}\): Writing a Piecewise Function
Um museu cobra $5 por pessoa por uma visita guiada com um grupo de 1 a 9 pessoas ou uma taxa fixa de $50 para um grupo de 10 ou mais pessoas. Escreva uma função relacionando o número de pessoas\(n\),, ao custo,\(C\).
Solução
Serão necessárias duas fórmulas diferentes. Para\(n\) -valores abaixo de 10,\(C=5n\). Para valores de n que são 10 ou maiores,\(C=50\).
\[C(n)= \begin{cases} 5n & \text{if $n < 10$} \\ 50 &\text{if $n\geq10$} \end{cases} \nonumber \]
Análise
A função está representada na Figura\(\PageIndex{20}\). O gráfico é uma linha diagonal de\(n=0\) a\(n=10\) e uma constante depois disso. Neste exemplo, as duas fórmulas concordam no ponto de encontro em que\(n=10\), mas nem todas as funções por partes, têm essa propriedade.
![[Gráfico de C (n).]](https://math.libretexts.org/@api/deki/files/894/CNX_Precalc_Figure_01_02_021.jpg)
Exemplo\(\PageIndex{8B}\): Working with a Piecewise Function
Uma empresa de telefonia celular usa a função abaixo para determinar o custo, C, em dólares para g gigabytes de transferência de dados.
\[C(g)= \begin{cases} 25 & \text{if $0<g<2$} \\ 25+10(g-2) &\text{if $g\geq2$} \end{cases} \nonumber \]
Encontre o custo do uso de 1,5 gigabytes de dados e o custo do uso de 4 gigabytes de dados.
Solução
Para descobrir o custo do uso de 1,5 gigabytes de dados\(C(1.5)\), primeiro examinamos em qual parte do domínio nossa entrada se enquadra. Como 1,5 é menor que 2, usamos a primeira fórmula.
\[C(1.5)=$25 \nonumber \]
Para encontrar o custo de usar 4 gigabytes de dados, C (4), vemos que nossa entrada de 4 é maior que 2, então usamos a segunda fórmula.
\[C(4)=25+10(4−2)=$45 \nonumber \]
Análise
A função está representada na Figura\(\PageIndex{21}\). Podemos ver onde a função muda de uma constante para uma identidade deslocada e ampliada\(g=2\). Traçamos os gráficos das diferentes fórmulas em um conjunto comum de eixos, garantindo que cada fórmula seja aplicada em seu domínio adequado.
![[Gráfico de C (g)]](https://math.libretexts.org/@api/deki/files/895/CNX_Precalc_Figure_01_02_022.jpg)
![]() Dada uma função por partes, desenhe um gráfico.
Dada uma função por partes, desenhe um gráfico.
- Indique no eixo x os limites definidos pelos intervalos em cada parte do domínio.
- Para cada parte do domínio, faça um gráfico desse intervalo usando a equação correspondente pertencente a essa peça. Não represente graficamente duas funções em um intervalo, pois isso violaria os critérios de uma função.
Exemplo\(\PageIndex{8C}\): Graphing a Piecewise Function
Esboce um gráfico da função.
\[f(x)= \begin{cases} x^2 & \text{if $x \leq 1$} \\ 3 &\text{if $1<x\leq2$} \\ x &\text{if $x>2$} \end{cases} \nonumber \]
Solução
Cada uma das funções do componente é da nossa biblioteca de funções do kit de ferramentas, então conhecemos suas formas. Podemos imaginar representar graficamente cada função e, em seguida, limitar o gráfico ao domínio indicado. Nos pontos finais do domínio, desenhamos círculos abertos para indicar onde o ponto final não está incluído devido a uma desigualdade menor ou maior que; desenhamos um círculo fechado em que o ponto final é incluído devido a uma desigualdade menor ou igual a ou maior que ou igual a.
A figura\(\PageIndex{20}\) mostra os três componentes da função por partes representados graficamente em sistemas de coordenadas separados.
![[Gráfico de cada parte da função por partes f (x)]](https://math.libretexts.org/@api/deki/files/896/CNX_Precalc_Figure_01_02_023abc.jpg)
Figura\(\PageIndex{20}\): Gráfico de cada parte da função por partes f (x)
(a)\( f(x)=x^2\) se\(x≤1\); (b)\(f(x)=3\) se\(1< x≤2\); (c)\(f(x)=x\) se\(x>2\)
Agora que esboçamos cada peça individualmente, nós as combinamos no mesmo plano de coordenadas. Veja a Figura\(\PageIndex{21}\).
![[Gráfico de toda a função.]](https://math.libretexts.org/@api/deki/files/897/CNX_Precalc_Figure_01_02_026.jpg)
Análise
Observe que o gráfico passa no teste da linha vertical mesmo em\(x=1\) e\(x=2\) porque os pontos\((1,3)\) não\((2,2)\) fazem parte do gráfico da função, embora\((1,1)\) e\((2, 3)\) sejam.
Exercício\(\PageIndex{8}\)
Faça um gráfico da seguinte função por partes.
\[f(x)= \begin{cases} x^3 & \text{if $x < -1$} \\ -2 &\text{if $-1<x<4$} \\ \sqrt{x} &\text{if $x>4$} \end{cases} \nonumber \]
- Responda
-
![[Gráfico de f (x).]](https://math.libretexts.org/@api/deki/files/898/CNX_Precalc_Figure_01_02_027.jpg)
Figura\(\PageIndex{22}\)
![]() Mais de uma fórmula de uma função por partes pode ser aplicada a um valor no domínio?
Mais de uma fórmula de uma função por partes pode ser aplicada a um valor no domínio?
Não. Cada valor corresponde a uma equação em uma fórmula por partes.
Conceitos chave
- O domínio de uma função inclui todos os valores de entrada reais que não nos levariam a tentar uma operação matemática indefinida, como dividir por zero ou obter a raiz quadrada de um número negativo.
- O domínio de uma função pode ser determinado listando os valores de entrada de um conjunto de pares ordenados.
- O domínio de uma função também pode ser determinado identificando os valores de entrada de uma função escrita como uma equação.
- Os valores de intervalo representados em uma linha numérica podem ser descritos usando notação de desigualdade, notação de construtor de conjuntos e notação de intervalo.
- Para muitas funções, o domínio e o intervalo podem ser determinados a partir de um gráfico.
- Uma compreensão das funções do kit de ferramentas pode ser usada para encontrar o domínio e a variedade de funções relacionadas.
- Uma função por partes é descrita por mais de uma fórmula.
- Uma função por partes pode ser representada graficamente usando cada fórmula algébrica em seu subdomínio atribuído.
Notas de pé
1 Os números: onde os dados e a indústria cinematográfica se encontram. “História de bilheteria para filmes de terror”. http://www.the-numbers.com/market/genre/Horror. Acessado em 24/3/2014
2 www.eia.gov/dnav/pet/hist/lea... s=MCRFpak2&f=A.
Glossário
- notação de intervalo
-
um método para descrever um conjunto que inclui todos os números entre um limite inferior e um limite superior; os valores inferior e superior são listados entre colchetes ou parênteses, um colchete indicando inclusão no conjunto e um parêntese indicando exclusão
- função por partes
-
uma função na qual mais de uma fórmula é usada para definir a saída
- notação de construtor de conjuntos
-
um método de descrever um conjunto por meio de uma regra que todos os seus membros obedecem; assume a forma {x| declaração sobre x}


