9.6: Princípios de contagem
- Page ID
- 189485
- Resolva problemas de contagem usando o Princípio de Adição.
- Resolva problemas de contagem usando o Princípio de Multiplicação.
- Resolva problemas de contagem usando permutações envolvendo n objetos distintos.
- Resolva problemas de contagem usando combinações.
- Encontre o número de subconjuntos de um determinado conjunto.
- Resolva problemas de contagem usando permutações envolvendo n objetos não distintos.
Uma nova empresa vende capas personalizáveis para tablets e smartphones. Cada capa vem em uma variedade de cores e pode ser personalizada por uma taxa adicional com imagens ou um monograma. Um cliente pode optar por não personalizar ou pode optar por ter uma, duas ou três imagens ou um monograma. O cliente pode escolher a ordem das imagens e das letras no monograma. A empresa está trabalhando com uma agência para desenvolver uma campanha de marketing com foco no grande número de opções que ela oferece. Contar as possibilidades é um desafio!
Encontramos uma grande variedade de problemas de contagem todos os dias. Há um ramo da matemática dedicado ao estudo de problemas de contagem como este. Outras aplicações de contagem incluem senhas seguras, resultados de corridas de cavalos e opções de agendamento para faculdades. Examinaremos esse tipo de matemática nesta seção.
Usando o princípio da adição
A empresa que vende capas personalizáveis oferece capas para tablets e smartphones. Existem\(3\) modelos de tablets e modelos de smartphones\(5\) compatíveis. O Princípio de Adição nos diz que podemos adicionar o número de opções de tablet ao número de opções de smartphone para encontrar o número total de opções. Pelo Princípio da Adição, existem opções\(8\) totais, como podemos ver na Figura\(\PageIndex{1}\).
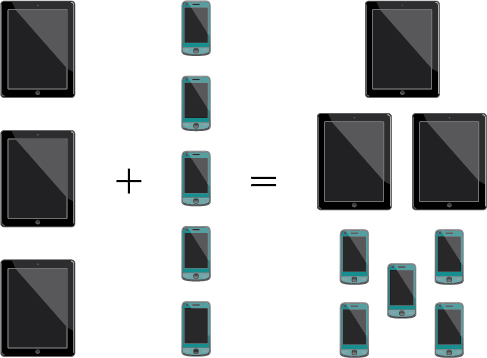
Figura\(\PageIndex{1}\)
De acordo com o Princípio da Adição, se um evento pode ocorrer de\(m\) várias maneiras e um segundo evento sem resultados comuns pode ocorrer de\(n\) maneiras, o primeiro ou o segundo evento pode ocorrer de\(m+n\) maneiras.
Há opções de\(2\) pratos vegetarianos e opções de entrada de\(5\) carne em um menu de jantar. Qual é o número total de opções de entrada?
Solução
Podemos adicionar o número de opções vegetarianas ao número de opções de carne para encontrar o número total de opções de pratos principais.

Existem opções\(7\) totais.
Um estudante está comprando um novo computador. Ele está decidindo entre computadores\(3\) desktop e\(4\) laptops. Qual é o número total de opções de computador?
- Responda
-
\(7\)
Usando o Princípio de Multiplicação
O Princípio de Multiplicação se aplica quando estamos fazendo mais de uma seleção. Suponha que estejamos escolhendo um aperitivo, uma entrada e uma sobremesa. Se houver opções de\(2\) aperitivos, opções de\(3\) entrada e opções de\(2\) sobremesas em um menu de jantar com preço fixo, há um total de opções\(12\) possíveis de uma, conforme mostrado no diagrama da árvore na Figura\(\PageIndex{2}\).
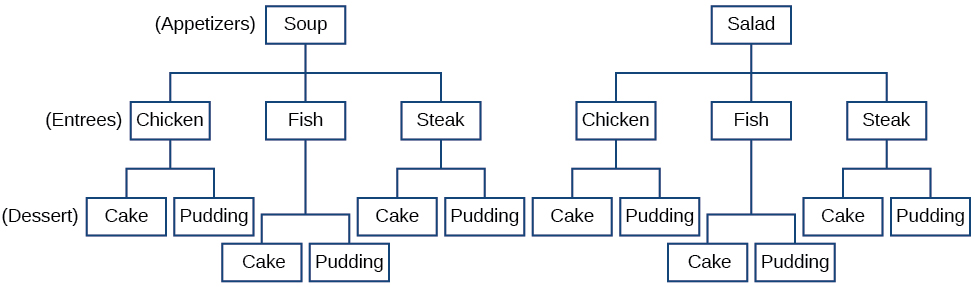
Figura\(\PageIndex{2}\)
As opções possíveis são:
- sopa, frango, bolo
- sopa, frango, pudim
- sopa, peixe, bolo
- sopa, peixe, pudim
- sopa, bife, bolo
- sopa, bife, pudim
- salada, frango, bolo
- salada, frango, pudim
- salada, peixe, bolo
- salada, peixe, pudim
- salada, bife, bolo
- salada, bife, pudim Também podemos encontrar o número total de jantares possíveis multiplicando.
Também podemos concluir que existem\(12\) possíveis opções de jantar simplesmente aplicando o Princípio de Multiplicação.
\(\# \text{of appetizer options} \times \# \text {of entree options} \times \# \text {of dessert options}\)
\(2 × 3 × 2=12\)
De acordo com o Princípio de Multiplicação, se um evento pode ocorrer de\(m\) várias maneiras e um segundo evento pode ocorrer de\(n\) maneiras após a ocorrência do primeiro evento, os dois eventos podem ocorrer de\(m×n\) maneiras. Isso também é conhecido como Princípio Fundamental de Contagem.
Diane embalou\(2\) saias,\(4\) blusas e um suéter para sua viagem de negócios. Ela precisará escolher uma saia e uma blusa para cada roupa e decidir se vai usar o suéter. Use o Princípio de Multiplicação para encontrar o número total de roupas possíveis.
Solução
Para saber o número total de roupas, encontre o produto do número de opções de saias, do número de opções de blusas e do número de opções de suéter.

Existem roupas\(16\) possíveis.
Um restaurante oferece um café da manhã especial que inclui um sanduíche de café da manhã, um acompanhamento e uma bebida. Existem\(3\) tipos de sanduíches de café da manhã, opções de\(4\) acompanhamentos e opções de\(5\) bebidas. Encontre o número total de possíveis especialidades de café da manhã.
- Responda
-
Existem\(60\) possíveis especialidades de café da manhã.
Encontrando o número de permutações de objetos\(n\) distintos
O Princípio de Multiplicação pode ser usado para resolver uma variedade de tipos de problemas. Um tipo de problema envolve colocar objetos em ordem. Organizamos letras em palavras e dígitos em números, fazemos fila para fotografias, decoramos salas e muito mais. Uma ordenação de objetos é chamada de permutação.
Encontrando o número de permutações de objetos\(n\) distintos usando o princípio de multiplicação
Para resolver problemas de permutação, geralmente é útil desenhar segmentos de linha para cada opção. Isso nos permite determinar o número de cada opção para que possamos multiplicar. Por exemplo, suponha que tenhamos quatro pinturas e queiramos descobrir o número de maneiras pelas quais podemos pendurar três das pinturas em ordem na parede. Podemos desenhar três linhas para representar os três lugares na parede.

Existem quatro opções para o primeiro lugar, então escrevemos um\(4\) na primeira linha.

Depois que o primeiro lugar for preenchido, há três opções para o segundo lugar, então escrevemos a\(3\) na segunda linha.
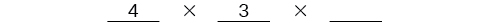
Depois que o segundo lugar for preenchido, há duas opções para o terceiro lugar, então escrevemos um\(2\) na terceira linha. Finalmente, encontramos o produto.
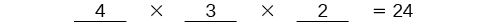
Há\(24\) possíveis permutações das pinturas.
- Determine quantas opções existem para a primeira situação.
- Determine quantas opções faltam para a segunda situação.
- Continue até que todos os pontos estejam preenchidos.
- Multiplique os números juntos.
Em uma competição de natação, nove nadadores competem em uma corrida.
- De quantas maneiras eles podem se posicionar em primeiro, segundo e terceiro?
- De quantas maneiras eles podem ficar em primeiro, segundo e terceiro lugar se um nadador chamado Ariel ganhar o primeiro lugar? (Suponha que haja apenas um concorrente chamado Ariel.)
- De quantas maneiras todos os nove nadadores podem se alinhar para tirar uma foto?
Solução
- Desenhe linhas para cada lugar.

Existem\(9\) opções para o primeiro lugar. Uma vez que alguém tenha conquistado o primeiro lugar,\(8\) restam opções para o segundo lugar. Uma vez conquistados o primeiro e o segundo lugar,\(7\) restam opções para o terceiro lugar.
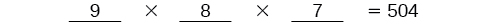
Multiplique para descobrir que existem\(504\) maneiras de os nadadores se posicionarem.
- Desenhe linhas para descrever cada lugar.
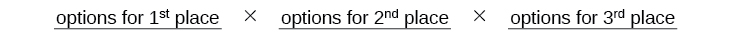
Sabemos que Ariel deve ganhar o primeiro lugar, então só há\(1\) opção para o primeiro lugar. \(8\)Restam opções para o segundo lugar e, em seguida, opções\(7\) restantes para o terceiro lugar.
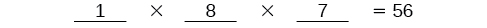
Multiplique para descobrir que existem\(56\) maneiras de os nadadores se posicionarem se Ariel vencer primeiro.
- Desenhe linhas para descrever cada lugar na foto.

Há\(9\) opções para o primeiro lugar, depois\(8\) para o segundo, para o terceiro,\(7\)\(6\) para o quarto, e assim por diante, até que reste apenas\(1\) uma pessoa para a última vaga.
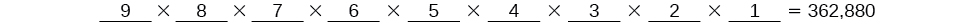
Existem\(362,880\) possíveis permutações para os nadadores se alinharem.
Análise
Observe que na parte c, descobrimos que havia\(9!\) maneiras de as\(9\) pessoas se alinharem. O número de permutações de objetos\(n\) distintos sempre pode ser encontrado por\(n!\).
Uma família de cinco pessoas está tirando retratos. Use o Princípio de Multiplicação para encontrar o seguinte:
- De quantas maneiras a família pode se alinhar para o retrato?
- De quantas maneiras o fotógrafo pode alinhar os membros da\(3\) família?
- De quantas maneiras a família pode fazer fila para o retrato se os pais precisarem ficar em cada extremidade?
- Responda a
-
\(120\)
- Resposta b
-
\(60\)
- Resposta c
-
\(12\)
Encontrando o número de permutações de n objetos distintos usando uma fórmula
Para alguns problemas de permutação, é inconveniente usar o Princípio de Multiplicação porque há muitos números para multiplicar. Felizmente, podemos resolver esses problemas usando uma fórmula. Antes de aprendermos a fórmula, vamos analisar duas notações comuns para permutações. Se tivermos um conjunto de\(n\) objetos e quisermos escolher\(r\) objetos do conjunto em ordem, escrevemos\(P(n,r)\). Outra forma de escrever isso é\(nP_r\) uma notação comumente vista em computadores e calculadoras. Para calcular\(P(n,r)\), começamos\(n!\) encontrando o número de maneiras de alinhar todos os nn objetos. Em seguida, dividimos por\((n−r)!\) para cancelar os\((n−r)\) itens que não desejamos alinhar.
Vamos ver como isso funciona com um exemplo simples. Imagine um clube de seis pessoas. Eles precisam eleger um presidente, um vice-presidente e um tesoureiro. Seis pessoas podem ser eleitas presidente, qualquer uma das cinco pessoas restantes pode ser eleita vice-presidente e qualquer uma das quatro pessoas restantes pode ser eleita tesoureira. O número de maneiras pelas quais isso pode ser feito é\(6×5×4=120\). Usando fatoriais, obtemos o mesmo resultado.
\(\dfrac{6!}{3!}=\dfrac{6·5·4·3!}{3!}=6·5·4=120 \)
Existem\(120\) maneiras de selecionar\(3\) dirigentes em ordem de um clube com\(6\) sócios. Nós nos referimos a isso como uma permutação de\(6\) tomada\(3\) de cada vez. A fórmula geral é a seguinte.
\[P(n,r)=\dfrac{n!}{(n−r)!}\]
Observe que a fórmula ainda funciona se estivermos escolhendo todos os\(n\) objetos e colocando-os em ordem. Nesse caso, estaríamos dividindo por\((n−n)!\) ou\(0!\), o que dissemos anteriormente é igual\(1\) a. Portanto, o número de permutações de\(n\) objetos obtidos por\(n\) vez é\(\dfrac{n!}{1}\) ou apenas\(n!\).
Dados objetos\(n\) distintos, o número de maneiras de selecionar\(r\) objetos do conjunto em ordem é
\[P(n,r)=\dfrac{n!}{(n−r)!}\]
- Identifique a\(n\) partir das informações fornecidas.
- Identifique a\(r\) partir das informações fornecidas.
- Substitua\(n\) e\(r\) na fórmula pelos valores fornecidos.
- Avalie.
Um professor está criando um exame de\(9\) perguntas a partir de um banco de testes de\(12\) perguntas. De quantas maneiras ela pode selecionar e organizar as perguntas?
Solução
Substitua\(n=12\) e\(r=9\) entre na fórmula de permutação e simplifique.
\[\begin{align*} P(n,r)&=\dfrac{n!}{(n-r)!}\\ P(12,9)&=\dfrac{12!}{(12-9)!}\\ &=\dfrac{12!}{3!}\\ &=79,833,600 \end{align*}\]
Existem\(79,833,600\) possíveis permutações de perguntas do exame!
Análise
Também podemos usar uma calculadora para encontrar permutações. Para esse problema, entraríamos, pressionaríamos a\(nP_r\) função\(12\), entraríamos e\(9\), em seguida, pressionaríamos o sinal de igual. A\(nP_r\) função pode estar localizada no menu MATH com comandos de probabilidade.
Poderíamos ter resolvido o exemplo acima usando o Princípio de Multiplicação?
Sim. Poderíamos ter multiplicado\(15⋅14⋅13⋅12⋅11⋅10⋅9⋅8⋅7⋅6⋅5⋅4\) para encontrar a mesma resposta.
Uma peça tem um elenco de\(7\) atores se preparando para fazer sua chamada de cortina. Use a fórmula de permutação para encontrar o seguinte.
De quantas maneiras os\(7\) atores podem se alinhar?
- Responda
-
\(P(7,7)=5,040\)
De quantas maneiras os\(7\) atores podem\(5\) ser escolhidos para se alinhar?
- Responda
-
\(P(7,5)=2,520\)
Encontre o número de combinações usando a fórmula
Até agora, analisamos problemas solicitando que coloquemos objetos em ordem. Há muitos problemas em que queremos selecionar alguns objetos de um grupo de objetos, mas não nos importamos com a ordem. Quando estamos selecionando objetos e a ordem não importa, estamos lidando com combinações. Uma seleção de\(r\) objetos de um conjunto de\(n\) objetos em que a ordem não importa pode ser escrita como\(C(n,r)\). Assim como acontece com as permutações, também\(C(n,r)\) pode ser escrito como\(nC_r\). Nesse caso, a fórmula geral é a seguinte.
\[C(n,r)=\dfrac{n!}{r!(n−r)!} \label{combo}\]
Um problema anterior considerava a escolha\(3\) de\(4\) possíveis pinturas para pendurar na parede. Descobrimos que havia\(24\) maneiras\(3\) de selecionar as\(4\) pinturas em ordem. Mas e se não nos importássemos com o pedido? Esperaríamos um número menor porque selecionar pinturas\(1, 2, 3\) seria o mesmo que selecionar pinturas\(2, 3, 1\). Para descobrir o número de maneiras\(3\) de selecionar as\(4\) pinturas, desconsiderando a ordem das pinturas, divida o número de permutações pelo número de formas de ordenar\(3\) pinturas. Existem\(3!=3·2·1=6\) maneiras de encomendar\(3\) pinturas. Existem\(\dfrac{24}{6}\) ou\(4\) maneiras\(3\) de selecionar as\(4\) pinturas. Esse número faz sentido porque toda vez que estamos selecionando\(3\) pinturas, não estamos selecionando\(1\) pinturas. Existem\(4\) pinturas que poderíamos escolher não selecionar, então existem\(4\) maneiras\(3\) de selecionar as\(4\) pinturas.
Dados objetos\(n\) distintos, o número de maneiras de selecionar\(r\) objetos do conjunto é
\[C(n,r)=\dfrac{n!}{r!(n−r)!}\]
- Identifique a\(n\) partir das informações fornecidas.
- Identifique a\(r\) partir das informações fornecidas.
- Substitua\(n\) e\(r\) na fórmula pelos valores fornecidos.
- Avalie.
Um restaurante de fast food oferece cinco opções de acompanhamentos. Sua refeição vem com dois acompanhamentos.
- De quantas maneiras você pode selecionar seus acompanhamentos?
- De quantas maneiras você pode selecionar\(3\) acompanhamentos?
Solução
- Queremos escolher\(2\) acompanhamentos entre as\(5\) opções.
\(C(5,2)=\dfrac{5!}{2!(5−2)!}=10\)
- Queremos escolher\(3\) acompanhamentos entre as\(5\) opções.
\(C(5,3)=\dfrac{5!}{3!(5−3)!}=10\)
Análise
Também podemos usar uma calculadora gráfica para encontrar combinações. Digite 5, depois pressione\(nC_r\), digite 3 e, em seguida, pressione o sinal de igual. A função\(nC_r\), pode estar localizada no menu MATH com comandos de probabilidade.
É coincidência que as partes (a) e (b) do exemplo acima tenham as mesmas respostas?
Não. Quando escolhemos objetos r de n objetos, não estamos escolhendo\((n–r)\) objetos. Portanto,\(C(n,r)=C(n,n–r)\).
Uma sorveteria oferece\(10\) sabores de sorvete. Quantas maneiras existem de escolher\(3\) sabores para uma banana split?
- Responda
-
\(C(10,3)=120\)
Encontrando o número de subconjuntos de um conjunto
Examinamos apenas problemas de combinação nos quais escolhemos exatamente objetos rr. Em alguns problemas, queremos considerar a escolha de cada número possível de objetos. Considere, por exemplo, uma pizzaria que oferece\(5\) coberturas. Qualquer quantidade de coberturas pode ser solicitada. Quantas pizzas diferentes são possíveis?
Para responder a essa pergunta, precisamos considerar pizzas com qualquer número de coberturas. Existe uma\(C(5,0)=1\) maneira de pedir uma pizza sem coberturas. Existem\(C(5,1)=5\) maneiras de pedir uma pizza com exatamente uma cobertura. Se continuarmos esse processo, obteremos
\(C(5,0)+C(5,1)+C(5,2)+C(5,3)+C(5,4)+C(5,5)=32\)
Existem pizzas\(32\) possíveis. Esse resultado é igual\(2^5\) a.
Somos apresentados a uma sequência de escolhas. Para cada um dos nn objetos, temos duas opções: incluí-lo no subconjunto ou não. Então, para todo o subconjunto, fizemos nn escolhas, cada uma com duas opções. Portanto, há um total de\(2·2·2·…·2\) possíveis subconjuntos resultantes, desde o subconjunto vazio, que obtemos quando dizemos “não” a cada vez, até o conjunto original em si, que obtemos quando dizemos “sim” todas as vezes.
Um conjunto contendo n objetos distintos tem\(2^n\) subconjuntos.
Um restaurante oferece manteiga, queijo, cebolinha e creme de leite como coberturas para uma batata assada. Quantas maneiras diferentes existem de pedir uma batata?
Solução
Estamos procurando o número de subconjuntos de um conjunto com\(4\) objetos. \(n=4\)Substitua na fórmula.
\[\begin{align*} 2^n&=2^4\\ &=16 \end{align*}\]
Existem maneiras\(16\) possíveis de pedir uma batata.
Um bar de sundae em um casamento tem\(6\) coberturas para escolher. Qualquer número de coberturas pode ser escolhido. Quantos sundaes diferentes são possíveis?
- Responda
-
\(64\)sundaes
Encontrando o número de permutações de n objetos não distintos
Estudamos permutações em que todos os objetos envolvidos eram distintos. O que acontece se alguns dos objetos forem indistinguíveis? Por exemplo, suponha que haja uma folha de\(12\) adesivos. Se todos os adesivos fossem distintos, haveria\(12!\) maneiras de encomendá-los. No entanto,\(4\) dos adesivos são estrelas idênticas e\(3\) luas idênticas. Como nem todos os objetos são distintos, muitas das\(12!\) permutações que contamos são duplicatas. A fórmula geral para essa situação é a seguinte.
\[\dfrac{n!}{r_1!r_2!…r_k!}\]
Neste exemplo, precisamos dividir pelo número de maneiras de ordenar as\(4\) estrelas e as formas de ordenar as\(3\) luas para encontrar o número de permutações exclusivas dos adesivos. Existem\(4!\) formas de ordenar as estrelas e\(3!\) formas de ordenar a lua.
\(\dfrac{12!}{4!3!}=3,326,400\)
Existem\(3,326,400\) maneiras de solicitar a folha de adesivos.
Se houver nn elementos em um conjunto e\(r_1\) forem iguais,\(r_2\) forem iguais,\(r_3\) forem iguais e assim por diante\(r_k\), o número de permutações pode ser encontrado por
\[\dfrac{n!}{r_1!r_2!…r_k!}\]
Encontre o número de rearranjos das letras na palavra DISTINCT.
Solução
Existem\(8\) cartas. Ambos\(I\) e\(T\) se repetem\(2\) vezes. Substitua\(n=8\)\(r_1=2\),, e\(r_2=2\) na fórmula.
\(\dfrac{8!}{2!2!}=10,080\)
Existem\(10,080\) arranjos.
Encontre o número de rearranjos das letras na palavra CARRIER.
- Responda
-
\(840\)
Acesse esses recursos on-line para obter instruções e práticas adicionais com combinações e permutações.
Equações-chave
| número de permutações de objetos\(n\) distintos obtidos\(r\) ao mesmo tempo | \(P(n,r)=\dfrac{n!}{(n−r)!}\) |
| número de combinações de objetos\(n\) distintos capturados\(r\) ao mesmo tempo | \(C(n,r)=\dfrac{n!}{r!(n−r)!}\) |
| número de permutações de objetos\(n\) não distintos | \(\dfrac{n!}{r1!r2!…rk!}\) |
Conceitos-chave
- Se um evento pode ocorrer de\(m\) várias maneiras e um segundo evento sem resultados comuns pode ocorrer de\(n\) maneiras, então o primeiro ou o segundo evento pode ocorrer de\(m+n\) maneiras. Veja o exemplo\(\PageIndex{1}\).
- Se um evento pode ocorrer de\(m\) várias maneiras e um segundo evento pode ocorrer de\(n\) maneiras após a ocorrência do primeiro evento, os dois eventos podem ocorrer de\(m×n\) maneiras. Veja o exemplo\(\PageIndex{2}\).
- Uma permutação é uma ordenação de\(n\) objetos.
- Se tivermos um conjunto de\(n\) objetos e quisermos escolher\(r\) objetos do conjunto em ordem, escrevemos\(P(n,r)\).
- Os problemas de permutação podem ser resolvidos usando o Princípio de Multiplicação ou a fórmula para\(P(n,r)\). Veja o exemplo\(\PageIndex{3}\) e o exemplo\(\PageIndex{4}\).
- Uma seleção de objetos em que a ordem não importa é uma combinação.
- Dados objetos\(n\) distintos, o número de maneiras de selecionar\(r\) objetos do conjunto é\(C(n,r)\) e pode ser encontrado usando uma fórmula. Veja o exemplo\(\PageIndex{5}\).
- Um conjunto contendo objetos\(n\) distintos tem\(2n\) subconjuntos. Veja o exemplo\(\PageIndex{6}\).
- Para problemas de contagem envolvendo objetos não distintos, precisamos dividir para evitar contar permutações duplicadas. Veja o exemplo\(\PageIndex{7}\).


