9.4: Sequências geométricas
- Page ID
- 189475
- Encontre a proporção comum para uma sequência geométrica.
- Liste os termos de uma sequência geométrica.
- Use uma fórmula recursiva para uma sequência geométrica.
- Use uma fórmula explícita para uma sequência geométrica.
Muitos empregos oferecem um aumento anual do custo de vida para manter os salários consistentes com a inflação. Suponha, por exemplo, que um recém-formado encontre uma posição como gerente de vendas ganhando um salário anual de\($26,000\). Ele tem a promessa de um aumento no\(2\%\) custo de vida a cada ano. Seu salário anual em qualquer ano pode ser encontrado multiplicando seu salário do ano anterior por\(102\%\). Seu salário será\($26,520\) depois de um ano;\($27,050.40\) depois de dois anos;\($27,591.41\) depois de três anos; e assim por diante. Quando um salário aumenta em uma taxa constante a cada ano, o salário cresce por um fator constante. Nesta seção, analisaremos as sequências que crescem dessa forma.
Encontrando proporções comuns
Os valores salariais anuais descritos formam uma sequência geométrica porque mudam por um fator constante a cada ano. Cada termo de uma sequência geométrica aumenta ou diminui por um fator constante chamado razão comum. A sequência abaixo é um exemplo de uma sequência geométrica porque cada termo aumenta em um fator constante de 6. Multiplicar qualquer termo da sequência pela razão comum 6 gera o termo subsequente.

Uma sequência geométrica é aquela em que qualquer termo dividido pelo termo anterior é uma constante. Essa constante é chamada de proporção comum da sequência. A proporção comum pode ser encontrada dividindo qualquer termo na sequência pelo termo anterior. Se\(a_1\) for o termo inicial de uma sequência geométrica e\(r\) for a razão comum, a sequência será
\[\{a_1, a_1r,a_1r^2,a_1r^3,...\} .\]
- Divida cada termo pelo termo anterior.
- Compare os quocientes. Se forem iguais, existe uma proporção comum e a sequência é geométrica.
A sequência é geométrica? Em caso afirmativo, encontre a proporção comum.
- \(1\),\(2\)\(4\),\(8\),\(16\),...
- \(48\),\(12\)\(4\),\(2\),...
Solução
Divida cada termo pelo termo anterior para determinar se existe uma proporção comum.
- \(\dfrac{2}{1}=2\)\(\dfrac{4}{2}=2\)\(\dfrac{8}{4}=2\)\(\dfrac{16}{8}=2\)
A sequência é geométrica porque há uma proporção comum. A proporção comum é\(2\).
- \(\dfrac{12}{48}=\dfrac{1}{4}\)\(\dfrac{4}{12}=\dfrac{1}{3}\)\(\dfrac{2}{4}=\dfrac{1}{2}\)
A sequência não é geométrica porque não há uma proporção comum.
Análise
O gráfico de cada sequência é mostrado na Figura\(\PageIndex{1}\). Parece pelos gráficos que tanto (a) quanto (b) aparecem na forma do gráfico de uma função exponencial nesta janela de visualização. No entanto, sabemos que (a) é geométrico e, portanto, essa interpretação é válida, mas (b) não é.
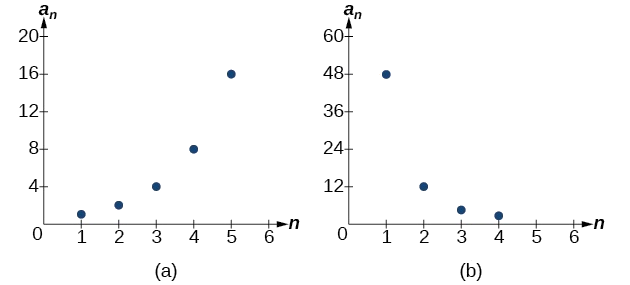
Figura\(\PageIndex{1}\)
Se lhe disserem que uma sequência é geométrica, você precisa dividir cada termo pelo termo anterior para encontrar a proporção comum?
Não. Se você souber que a sequência é geométrica, você pode escolher qualquer termo na sequência e dividi-lo pelo termo anterior para encontrar a proporção comum.
A sequência é geométrica? Em caso afirmativo, encontre a proporção comum.
\(5\),\(10\)\(15\),\(20\),...
- Responda
-
A sequência não é geométrica porque\(\dfrac{10}{5}≠\dfrac{15}{10}\)
A sequência é geométrica? Em caso afirmativo, encontre a proporção comum.
\(100\),\(20\)\(4\),\(\dfrac{4}{5}\),...
- Responda
-
A sequência é geométrica. A proporção comum é\(\dfrac{1}{5}\)
Escrevendo termos de sequências geométricas
Agora que podemos identificar uma sequência geométrica, aprenderemos como encontrar os termos de uma sequência geométrica se recebermos o primeiro termo e a razão comum. Os termos de uma sequência geométrica podem ser encontrados começando com o primeiro termo e multiplicando-se repetidamente pela razão comum. Por exemplo, se o primeiro termo de uma sequência geométrica for\(a_1=−2\) e a razão comum for\(r=4\), podemos encontrar termos subsequentes multiplicando\(−2⋅4\) para obter e\(−8\) depois multiplicando o resultado\(−8⋅4\) para obter\(−32\) e assim por diante.
\[\begin{align*} a_1 &= −2 \\ a_2 &= (−2⋅4)=−8 \\ a_3 &= (−8⋅4)=−32 \\ a_4 &= (−32⋅4)=128 \end{align*}\]
Os primeiros quatro termos são\(\{–2, –8, –32, –128\}\).
- Multiplique o termo inicial,\(a_1\), pela proporção comum para encontrar o próximo termo,\(a_2\).
- Repita o processo, usando\(a_n=a_2\) para localizar\(a_3\) e depois usar\(a_3\) para localizar\(a_4\), até que todos os quatro termos tenham sido identificados.
- Escreva os termos separados por comuns entre colchetes.
Liste os primeiros quatro termos da sequência geométrica com\(a_1=5\)\(r=–2\) e.
Solução
Multiplique\(a_1\) por\(−2\) para encontrar\(a_2\). Repita o processo, usando\(a_2\) para localizar\(a_3\) e assim por diante.
\[\begin{align*} a_1 &= 5 \\ a_2 &= −2a_1=−10 \\ a_3 &= −2a_2=20 \\ a_4 &= −2a_3=−40 \end{align*}\]
Os primeiros quatro termos são\(\{5,–10,20,–40\}\).
Liste os primeiros cinco termos da sequência geométrica com\(a_1=18\)\(r=\dfrac{1}{3}\) e.
- Responda
-
\(\left \{18, 6, 2, \dfrac{2}{3}, \dfrac{2}{9} \right \} \)
Usando fórmulas recursivas para sequências geométricas
Uma fórmula recursiva nos permite encontrar qualquer termo de uma sequência geométrica usando o termo anterior. Cada termo é o produto da proporção comum e do termo anterior. Por exemplo, suponha que a proporção comum seja\(9\). Então, cada termo é nove vezes o termo anterior. Como acontece com qualquer fórmula recursiva, o termo inicial deve ser fornecido.
A fórmula recursiva para uma sequência geométrica com razão comum r e primeiro termo\(a_1\) é
\[a_n=ra_{n−1},\;\;\; n≥2\]
- Indique o termo inicial.
- Encontre a proporção comum dividindo qualquer termo pelo termo anterior.
- Substitua a proporção comum na fórmula recursiva por uma sequência geométrica.
Escreva uma fórmula recursiva para a seguinte sequência geométrica.
\(\{6, 9, 13.5, 20.25, ...\} \nonumber\)
Solução
O primeiro termo é dado como\(6\). A proporção comum pode ser encontrada dividindo o segundo termo pelo primeiro termo.
\(r=\dfrac{9}{6}=1.5 \nonumber\)
Substitua a proporção comum na fórmula recursiva para sequências geométricas e defina\(a_1\).
\[\begin{align*} a_n &= ra_{n−1} \\ a_n &= 1.5a_{n−1} \text{ for }n≥2 \\ a_1 &= 6 \end{align*}\]
Análise
A sequência de pontos de dados segue um padrão exponencial. A razão comum também é a base de uma função exponencial, conforme mostrado na Figura\(\PageIndex{2}\).
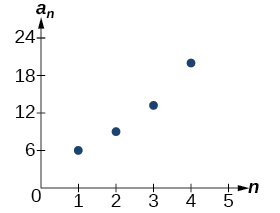
Figura\(\PageIndex{2}\)
Temos que dividir o segundo termo pelo primeiro termo para encontrar a proporção comum?
Não. Podemos dividir qualquer termo na sequência pelo termo anterior. No entanto, é mais comum dividir o segundo termo pelo primeiro, porque geralmente é o método mais fácil de encontrar a proporção comum.
Escreva uma fórmula recursiva para a seguinte sequência geométrica.
\(\{2, 43, 89, 1627, ...\}\)
- Responda
-
\(\begin{align*}a_1 &= 2 \\ a_n &= \dfrac{2}{3}a_{n−1} \text{ for }n≥2 \end{align*}\)
Usando fórmulas explícitas para sequências geométricas
Como uma sequência geométrica é uma função exponencial cujo domínio é o conjunto de números inteiros positivos e a razão comum é a base da função, podemos escrever fórmulas explícitas que nos permitem encontrar termos específicos.
\[a_n=a_1r^{n−1}\]
Vamos dar uma olhada na sequência\(\{18, 36, 72, 144, 288, ...\}\). Esta é uma sequência geométrica com uma proporção comum de\(2\) e uma função exponencial com uma base de\(2\). Uma fórmula explícita para essa sequência é
\(a_n=18·2^{n−1}\)
O gráfico da sequência é mostrado na Figura\(\PageIndex{3}\).
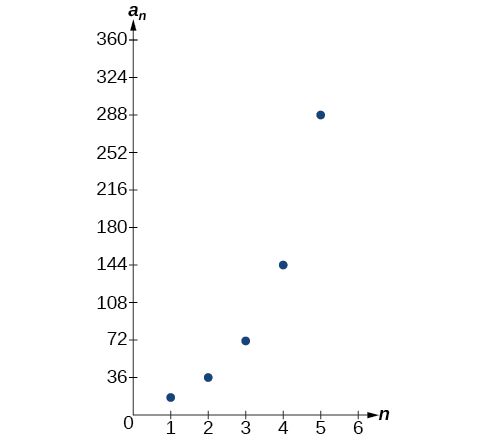
Figura\(\PageIndex{3}\)
O\(n^{th}\) termo de uma sequência geométrica é dado pela fórmula explícita:
\[a_n=a_1r^{n−1}\]
Dada uma sequência geométrica com\(a_1=3\) e\(a_4=24\), encontre\(a_2\).
Solução
A sequência pode ser escrita em termos do termo inicial e da proporção comum\(r\).
\(3\),\(3r\)\(3r^2\),\(3r^3\),...
Encontre a proporção comum usando o quarto termo fornecido.
\[\begin{align*} a_n&=a_1r^{n-1} \\ a_4&=3r^3 \qquad \text{Write the fourth term of sequence in terms of }\alpha_1 \text{ and } r \\ 24&=3r^3 \qquad \text{Substitute }24 \text{ for }a_4 \\ 8&=r^3 \qquad \text{Divide} \\ r&=2 \qquad \text{Solve for the common ratio} \end{align*}\]
Encontre o segundo termo multiplicando o primeiro termo pela proporção comum.
\[\begin{align*} a_2 &= 2 \\ a_1 &= 2(3) \\ & = 6 \end{align*}\]
Análise
A proporção comum é multiplicada pelo primeiro termo uma vez para encontrar o segundo termo, duas vezes para encontrar o terceiro termo, três vezes para encontrar o quarto termo e assim por diante. O décimo termo pode ser encontrado multiplicando o primeiro termo pela razão comum nove vezes ou multiplicando pela proporção comum elevada à nona potência.
Dada uma sequência geométrica com\(a_2=4\) e\(2a_3=32\), encontre\(a_6\).
- Responda
-
\(a_6=16,384\)
Escreva uma fórmula explícita para o enésimo termo da seguinte sequência geométrica.
\(\{2, 10, 50, 250, ...\}\)
Solução
O primeiro termo é\(2\). A proporção comum pode ser encontrada dividindo o segundo termo pelo primeiro termo.
\(\dfrac{10}{2}=5\)
A proporção comum é\(5\). Substitua a proporção comum e o primeiro termo da sequência na fórmula.
\[\begin{align*}a_n &= a_1r^{(n−1)} \\ a_n &= 2⋅5^{n−1} \end{align*}\]
O gráfico dessa sequência na Figura\(\PageIndex{4}\) mostra um padrão exponencial.
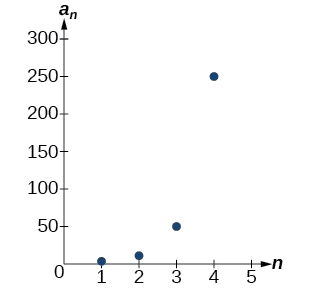
Figura\(\PageIndex{4}\)
Escreva uma fórmula explícita para a seguinte sequência geométrica.
\(\{–1, 3, –9, 27, ...\}\)
- Responda
-
\(a_n=−{(−3)}^{n−1}\)
Resolvendo problemas de aplicação com sequências geométricas
Em cenários reais envolvendo sequências aritméticas, talvez precisemos usar um termo inicial de\(a_0\) em vez de\(a_1\). Nesses problemas, podemos alterar ligeiramente a fórmula explícita usando a seguinte fórmula:
\(a_n=a_0r^n\)
Em 2013, o número de estudantes em uma escola pequena é\(284\). Estima-se que a população estudantil aumente a\(4\%\) cada ano.
- Escreva uma fórmula para a população estudantil.
- Estime a população estudantil em 2020.
Solução
- A situação pode ser modelada por uma sequência geométrica com um termo inicial de\(284\). A população estudantil será\(104\%\) do ano anterior, então a proporção comum é\(1.04\).
\(P\)Seja a população estudantil e\(n\) seja o número de anos após 2013. Usando a fórmula explícita para uma sequência geométrica, obtemos
\(P_n =284⋅{1.04}^n\)
- Podemos encontrar o número de anos desde 2013 subtraindo.
\(2020−2013=7\)
Estamos procurando a população depois de\(7\) anos. Podemos substituir\(7\) para\(n\) estimar a população em 2020.
\(P_7=284⋅{1.04}^7≈374\)
A população estudantil será de aproximadamente\(374\) em 2020.
Uma empresa inicia um novo site. Inicialmente, o número de acessos se\(293\) deve ao fator curiosidade. A empresa estima que o número de acessos aumentará\(2.6%\) por semana.
- Escreva uma fórmula para o número de acertos.
- Estime o número de acessos em\(5\) semanas.
- Responda a
-
\(P_n = 293⋅1.026a^n\)
- Resposta b
-
O número de acessos será de aproximadamente\(333\).
Acesse esses recursos on-line para obter instruções e práticas adicionais com sequências geométricas.
Equações-chave
| fórmula recursiva para o enésimo termo de uma sequência geométrica | \(a_n=ra_{n−1}\),\(n≥2\) |
| fórmula explícita para o enésimo termo de uma sequência geométrica | \(a_n=a_1r^{n−1}\) |
Conceitos-chave
- Uma sequência geométrica é uma sequência na qual a razão entre quaisquer dois termos consecutivos é uma constante.
- A razão constante entre dois termos consecutivos é chamada de razão comum.
- A proporção comum pode ser encontrada dividindo qualquer termo na sequência pelo termo anterior. Veja o exemplo\(\PageIndex{1}\).
- Os termos de uma sequência geométrica podem ser encontrados começando com o primeiro termo e multiplicando-se repetidamente pela razão comum. Veja o exemplo\(\PageIndex{2}\) e o exemplo\(\PageIndex{4}\).
- Uma fórmula recursiva para uma sequência geométrica com proporção comum\(r\) é dada\(a_n=ra_{n–1}\) por for\(n≥2\).
- Como acontece com qualquer fórmula recursiva, o termo inicial da sequência deve ser dado. Veja o exemplo\(\PageIndex{3}\).
- Uma fórmula explícita para uma sequência geométrica com proporção comum\(r\) é dada por\(a_n=a_1r^{n–1}\). Veja o exemplo\(\PageIndex{5}\).
- Em problemas de aplicação, às vezes alteramos ligeiramente a fórmula explícita para\(a_n=a_0r^n\). Veja o exemplo\(\PageIndex{6}\).


