8.6: Seções cônicas em coordenadas polares
- Page ID
- 189257
- Identifique uma cônica na forma polar.
- Representar graficamente as equações polares das cônicas.
- Defina cônicas em termos de foco e diretriz.
A maioria de nós está familiarizada com o movimento orbital, como o movimento de um planeta ao redor do sol ou de um elétron ao redor de um núcleo atômico. Dentro do sistema planetário, as órbitas de planetas, asteróides e cometas ao redor de um corpo celeste maior geralmente são elípticas. Os cometas, no entanto, podem assumir uma órbita parabólica ou hiperbólica. E, na realidade, as características das órbitas dos planetas podem variar com o tempo. Cada órbita está ligada à localização do corpo celeste que está sendo orbitado e à distância e direção do planeta ou outro objeto desse corpo. Como resultado, tendemos a usar coordenadas polares para representar essas órbitas.
Em uma órbita elíptica, a periapsis é o ponto em que os dois objetos estão mais próximos, e a apoapse é o ponto em que eles estão mais afastados. Geralmente, a velocidade do corpo em órbita tende a aumentar à medida que se aproxima da periapsis e a diminuir à medida que se aproxima da apoapse. Alguns objetos atingem uma velocidade de escape, o que resulta em uma órbita infinita. Esses corpos exibem uma órbita parabólica ou hiperbólica em torno de um corpo; o corpo em órbita se liberta da atração gravitacional do corpo celeste e dispara para o espaço. Cada uma dessas órbitas pode ser modelada por uma seção cônica no sistema de coordenadas polares.
Identificando uma cônica na forma polar
Qualquer cônica pode ser determinada por três características: um único foco, uma linha fixa chamada diretriz e a razão entre as distâncias de cada uma e um ponto no gráfico. Considere a parábola\(x=2+y^2\) mostrada na Figura\(\PageIndex{2}\).
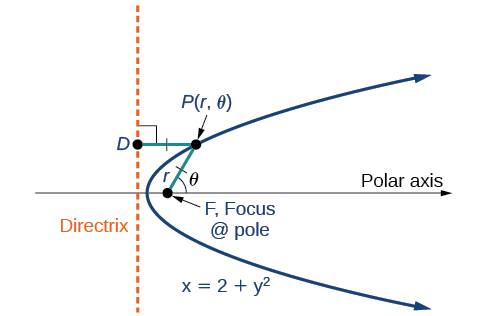
Anteriormente, aprendemos como uma parábola é definida pelo foco (um ponto fixo) e pela diretriz (uma linha fixa). Nesta seção, aprenderemos como definir qualquer cônica no sistema de coordenadas polares em termos de um ponto fixo, o foco\(P(r,\theta)\) no polo e uma linha, a diretriz, que é perpendicular ao eixo polar.
Se\(F\) é um ponto fixo, o foco, e\(D\) é uma linha fixa, a diretriz, então podemos deixar\(e\) ser um número positivo fixo, chamado de excentricidade, que podemos definir como a razão das distâncias de um ponto no gráfico para o foco e o ponto no gráfico para o diretriz. Em seguida, o conjunto de todos os pontos\(P\), de forma que\(e=\dfrac{PF}{PD}\) seja cônica. Em outras palavras, podemos definir uma cônica como o conjunto de todos os pontos\(P\) com a propriedade de que a razão entre\(P\) a distância de e\(F\) a distância de\(P\) até\(D\) é igual à constante\(e\).
Para uma cônica com excentricidade\(e\),
- se\(0≤e<1\), a cônica é uma elipse
- se\(e=1\), a cônica é uma parábola
- se\(e>1\), a cônica é uma hipérbole
Com essa definição, agora podemos definir uma cônica em termos da diretriz\(x=\pm p\), da excentricidade\(e\) e do ângulo\(\theta\). Assim, cada cônica pode ser escrita como uma equação polar, uma equação escrita em termos de\(r\)\(\theta\) e.
Para uma cônica com foco na origem, se a diretriz é\(x=\pm p\), onde\(p\) está um número real positivo e a excentricidade é um número real positivo\(e\), a cônica tem uma equação polar
\[r=\dfrac{ep}{1\pm e \cos \theta}\]
Para uma cônica com foco na origem, se a diretriz é\(y=\pm p\), onde\(p\) está um número real positivo e a excentricidade é um número real positivo\(e\), a cônica tem uma equação polar
\[r=\dfrac{ep}{1\pm e \sin \theta}\]
- Multiplique o numerador e o denominador pelo inverso da constante no denominador para reescrever a equação na forma padrão.
- Identifique a excentricidade\(e\) como o coeficiente da função trigonométrica no denominador.
- Compare\(e\) com\(1\) para determinar a forma da cônica.
- Determine a diretriz como\(x=p\) se o cosseno estivesse no denominador e\(y=p\) se o seno estivesse no denominador. Defina\(ep\) igual ao numerador na forma padrão para resolver\(x\) ou\(y\).
Para cada uma das equações a seguir, identifique a cônica com foco na origem, na diretriz e na excentricidade.
- \(r=\dfrac{6}{3+2 \sin \theta}\)
- \(r=\dfrac{12}{4+5 \cos \theta}\)
- \(r=\dfrac{7}{2−2 \sin \theta}\)
Solução
Para cada uma das três cônicas, reescreveremos a equação na forma padrão. A forma padrão tem a\(1\) como constante no denominador. Portanto, em todas as três partes, o primeiro passo será multiplicar o numerador e o denominador pelo inverso da constante da equação original,\(\dfrac{1}{c}\), onde\(c\) está essa constante.
- Multiplique o numerador e o denominador por\(\dfrac{1}{3}\).
\(r=\dfrac{6}{3+2\sin \theta}⋅\dfrac{\left(\dfrac{1}{3}\right)}{\left(\dfrac{1}{3}\right)}=\dfrac{6\left(\dfrac{1}{3}\right)}{3\left(\dfrac{1}{3}\right)+2\left(\dfrac{1}{3}\right)\sin \theta}=\dfrac{2}{1+\dfrac{2}{3} \sin \theta}\)
Porque\(\sin \theta\) está no denominador, a diretriz está\(y=p\). Comparando com a forma padrão, observe que\(e=\dfrac{2}{3}\) .Portanto, a partir do numerador,
\[\begin{align*} 2&=ep\\ 2&=\dfrac{2}{3}p\\ \left(\dfrac{3}{2}\right)2&=\left(\dfrac{3}{2}\right)\dfrac{2}{3}p\\ 3&=p \end{align*}\]
Desde então\(e<1\), a cônica é uma elipse. A excentricidade é\(e=\dfrac{2}{3}\) e a diretriz é\(y=3\).
- Multiplique o numerador e o denominador por\(\dfrac{1}{4}\).
\[\begin{align*} r&=\dfrac{12}{4+5 \cos \theta}\cdot \dfrac{\left(\dfrac{1}{4}\right)}{\left(\dfrac{1}{4}\right)}\\ r&=\dfrac{12\left(\dfrac{1}{4}\right)}{4\left(\dfrac{1}{4}\right)+5\left(\dfrac{1}{4}\right)\cos \theta}\\ r&=\dfrac{3}{1+\dfrac{5}{4} \cos \theta} \end{align*}\]
Porque\(\cos \theta\) está no denominador, a diretriz está\(x=p\). Comparando com o formulário padrão,\(e=\dfrac{5}{4}\). Portanto, a partir do numerador,
\[\begin{align*} 3&=ep\\ 3&=\dfrac{5}{4}p\\ \left(\dfrac{4}{5}\right)3&=\left(\dfrac{4}{5}\right)\dfrac{5}{4}p\\ \dfrac{12}{5}&=p \end{align*}\]
Desde então\(e>1\), a cônica é uma hipérbole. A excentricidade é\(e=\dfrac{5}{4}\) e a diretriz é\(x=\dfrac{12}{5}=2.4\).
- Multiplique o numerador e o denominador por\(\dfrac{1}{2}\).
\[\begin{align*} r&=\dfrac{7}{2-2 \sin \theta}\cdot \dfrac{\left(\dfrac{1}{2}\right)}{\left(\dfrac{1}{2}\right)}\\ r&=\dfrac{7\left(\dfrac{1}{2}\right)}{2\left(\dfrac{1}{2}\right)-2\left(\dfrac{1}{2}\right) \sin \theta}\\ r&=\dfrac{\dfrac{7}{2}}{1-\sin \theta} \end{align*}\]
Como o seno está no denominador, a diretriz está\(y=−p\). Comparando com o formulário padrão,\(e=1\). Portanto, a partir do numerador,
\[\begin{align*} \dfrac{7}{2}&=ep\\ \dfrac{7}{2}&=(1)p\\ \dfrac{7}{2}&=p \end{align*}\]
Porque\(e=1\) a cônica é uma parábola. A excentricidade é\(e=1\) e a diretriz é\(y=−\dfrac{7}{2}=−3.5\).
Identifique a cônica com foco na origem, a diretriz e a excentricidade de\(r=\dfrac{2}{3−\cos \theta}\).
- Resposta
-
elipse\(e=\dfrac{1}{3}\);\(x=−2\)
Representação gráfica das equações polares das cônicas
Ao representar graficamente em coordenadas cartesianas, cada seção cônica tem uma equação única. Esse não é o caso ao representar graficamente em coordenadas polares. Devemos usar a excentricidade de uma seção cônica para determinar qual tipo de curva representar graficamente e, em seguida, determinar suas características específicas. O primeiro passo é reescrever a cônica na forma padrão, como fizemos no exemplo anterior. Em outras palavras, precisamos reescrever a equação para que o denominador comece com\(1\). Isso nos permite determinar\(e\) e, portanto, a forma da curva. A próxima etapa é substituir valores\(\theta\) e resolvê-los para\(r\) traçar alguns pontos-chave. A configuração é\(\theta\) igual a\(0\)\(\dfrac{\pi}{2}\),\(\pi\), e\(\dfrac{3\pi}{2}\) fornece os vértices para que possamos criar um esboço aproximado do gráfico.
Gráfico\(r=\dfrac{5}{3+3 \cos \theta}\).
Solução
Primeiro, reescrevemos a cônica na forma padrão multiplicando o numerador e o denominador pelo inverso de\(3\), que é\(\dfrac{1}{3}\).
\[\begin{align*} r &= \dfrac{5}{3+3 \cos \theta}=\dfrac{5\left(\dfrac{1}{3}\right)}{3\left(\dfrac{1}{3}\right)+3\left(\dfrac{1}{3}\right)\cos \theta} \\ r &= \dfrac{\dfrac{5}{3}}{1+\cos \theta} \end{align*}\]
Porque\(e=1\), representaremos graficamente uma parábola com foco na origem. A função tem um\(\cos \theta\), e há um sinal de adição no denominador, então a diretriz é\(x=p\).
\[\begin{align*} \dfrac{5}{3}&=ep\\ \dfrac{5}{3}&=(1)p\\ \dfrac{5}{3}&=p \end{align*}\]
A diretriz é\(x=\dfrac{5}{3}\).
Traçar alguns pontos-chave, como na Tabela, nos\(\PageIndex{1}\) permitirá ver os vértices. Veja a Figura\(\PageIndex{3}\).
| UMA | B | C | D | |
|---|---|---|---|---|
| \(\theta\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) |
| \(r=\dfrac{5}{3+3 \cos \theta}\) | \(\dfrac{5}{6}≈0.83\) | \(\dfrac{5}{3}≈1.67\) | indefinida | \(\dfrac{5}{3}≈1.67\) |
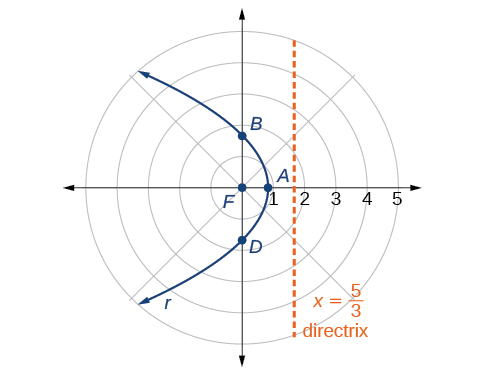
Podemos verificar nosso resultado com um utilitário gráfico. Veja a Figura\(\PageIndex{4}\).
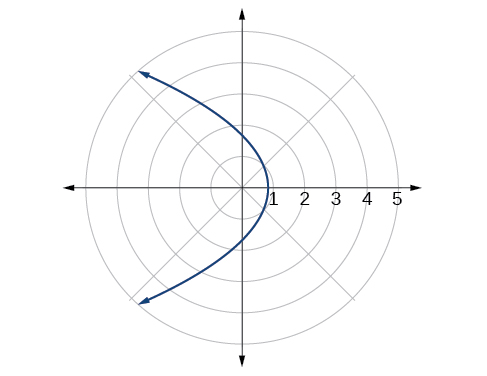
Gráfico\(r=\dfrac{8}{2−3 \sin \theta}\).
Solução
Primeiro, reescrevemos a cônica na forma padrão multiplicando o numerador e o denominador pelo inverso de\(2\), que é\(\dfrac{1}{2}\).
\[\begin{align*} r &=\dfrac{8}{2−3\sin \theta}=\dfrac{8\left(\dfrac{1}{2}\right)}{2\left(\dfrac{1}{2}\right)−3\left(\dfrac{1}{2}\right)\sin \theta} \\ r &= \dfrac{4}{1−\dfrac{3}{2} \sin \theta} \end{align*}\]
Porque\(e=\dfrac{3}{2}\), então\(e>1\), vamos representar graficamente uma hipérbole com foco na origem. A função tem um\(\sin \theta\) termo e há um sinal de subtração no denominador, então a diretriz é\(y=−p\).
\[\begin{align*} 4&=ep\\ 4&=\left(\dfrac{3}{2}\right)p\\ 4\left(\dfrac{2}{3}\right)&=p\\ \dfrac{8}{3}&=p \end{align*}\]
A diretriz é\(y=−\dfrac{8}{3}\).
Traçar alguns pontos-chave, como na Tabela, nos\(\PageIndex{2}\) permitirá ver os vértices. Veja a Figura\(\PageIndex{5}\).
| UMA | B | C | D | |
|---|---|---|---|---|
| \(\theta\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) |
| \(r=\dfrac{8}{2−3\sin \theta}\) | \(4\) | \(−8\) | \(4\) | \(\dfrac{8}{5}=1.6\) |
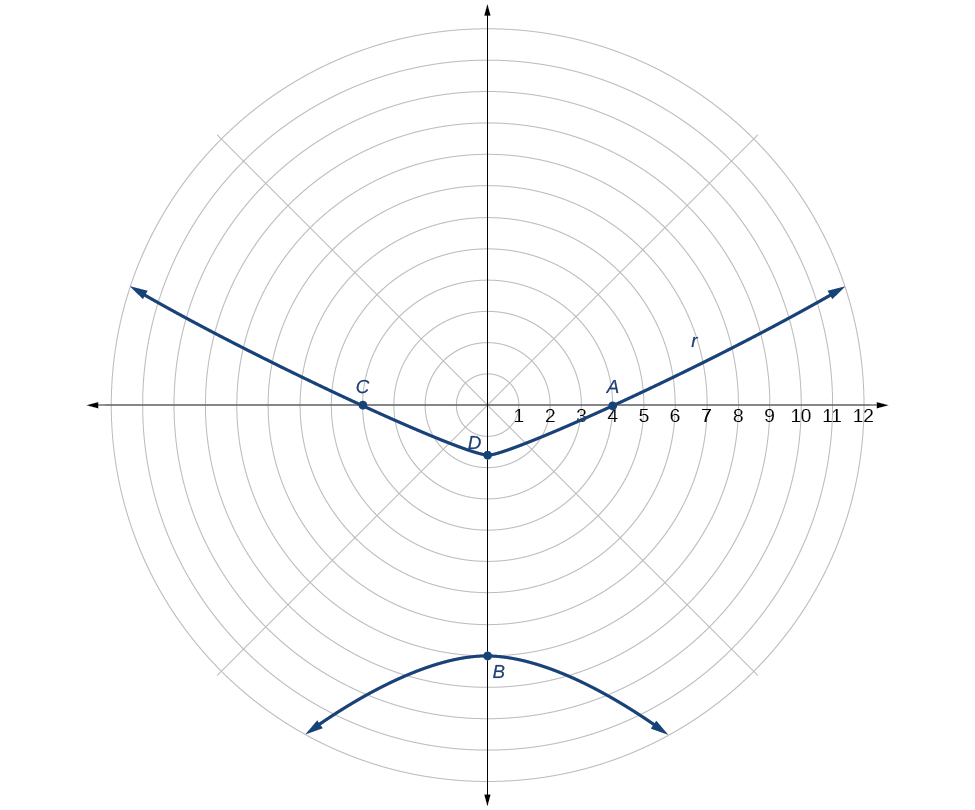
Gráfico\(r=\dfrac{10}{5−4 \cos \theta}\).
Solução
Primeiro, reescrevemos a cônica na forma padrão multiplicando o numerador e o denominador pelo inverso de 5, que é\(\dfrac{1}{5}\).
\[\begin{align*} r &= \dfrac{10}{5−4\cos \theta}=\dfrac{10\left(\dfrac{1}{5}\right)}{5\left(\dfrac{1}{5}\right)−4\left(\dfrac{1}{5}\right)\cos \theta} \\ r &= \dfrac{2}{1−\dfrac{4}{5} \cos \theta} \end{align*}\]
Porque\(e=\dfrac{4}{5}\)\(e<1\), então, vamos representar graficamente uma elipse com foco na origem. A função tem um\(\cos \theta\), e há um sinal de subtração no denominador, então a diretriz é\(x=−p\).
\[\begin{align*} 2&=ep\\ 2&=\left(\dfrac{4}{5}\right)p\\ 2\left(\dfrac{5}{4}\right)&=p\\ \dfrac{5}{2}&=p \end{align*}\]
A diretriz é\(x=−\dfrac{5}{2}\).
Traçar alguns pontos-chave, como na Tabela, nos\(\PageIndex{3}\) permitirá ver os vértices. Veja a Figura\(\PageIndex{6}\).
| UMA | B | C | D | |
|---|---|---|---|---|
| \(\theta\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) |
| \(r=\dfrac{10}{5−4 \cos \theta}\) | \(10\) | \(2\) | \(\dfrac{10}{9}≈1.1\) | \(2\) |
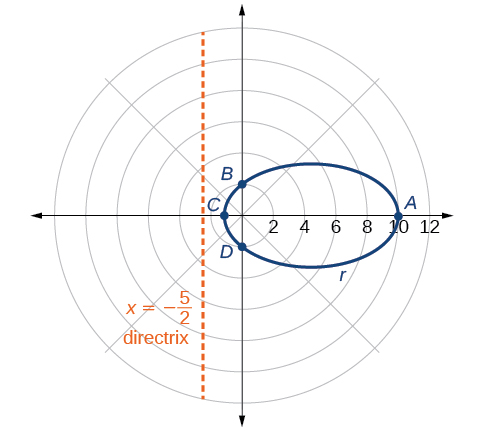
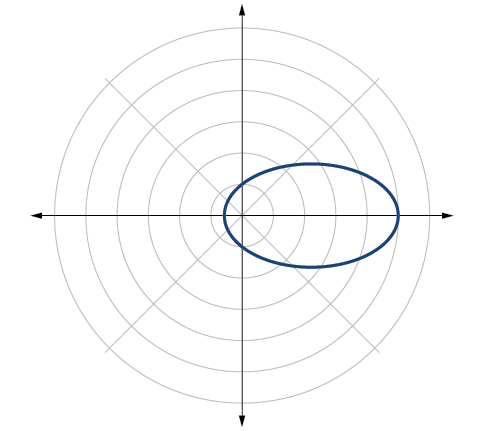
Análise
Podemos verificar nosso resultado usando um utilitário gráfico. Veja a Figura\(\PageIndex{7}\).
Gráfico\(r=\dfrac{2}{4−\cos \theta}\).
- Resposta
-
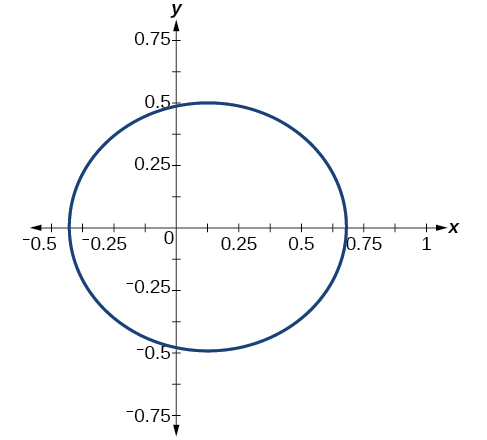
Figura\(\PageIndex{7}\)
Definindo cônicas em termos de um foco e uma diretriz
Até agora, usamos equações polares de cônicas para descrever e representar graficamente a curva. Agora trabalharemos ao contrário; usaremos informações sobre a origem, excentricidade e diretriz para determinar a equação polar.
- Determine se a diretriz é horizontal ou vertical. Se a diretriz for dada em termos de\(y\), usamos a forma polar geral em termos de seno. Se a diretriz for dada em termos de\(x\), usamos a forma polar geral em termos de cosseno.
- Determine o sinal no denominador. Se\(p<0\), use subtração. Se\(p>0\), use adição.
- Escreva o coeficiente da função trigonométrica como a excentricidade dada.
- Escreva o valor absoluto de\(p\) no numerador e simplifique a equação.
Encontre a forma polar da cônica com foco na origem\(e=3\) e na diretriz\(y=−2\).
Solução
A diretriz é\(y=−p\), então sabemos que a função trigonométrica no denominador é seno.
Porque\(y=−2\)\(–2<0\), então sabemos que há um sinal de subtração no denominador. Usamos a forma padrão de
\(r=\dfrac{ep}{1−e \sin \theta}\)
\(e=3\)e\(|−2|=2=p\) e.
Portanto,
\[\begin{align*} r&=\dfrac{(3)(2)}{1-3 \sin \theta}\\ r&=\dfrac{6}{1-3 \sin \theta} \end{align*}\]
Encontre a forma polar de uma cônica com foco na origem\(e=\dfrac{3}{5}\), e na diretriz\(x=4\).
Solução
Como a diretriz é\(x=p\), sabemos que a função no denominador é cosseno. Porque\(x=4\)\(4>0\), então sabemos que há um sinal de adição no denominador. Usamos a forma padrão de
\(r=\dfrac{ep}{1+e \cos \theta}\)
\(e=\dfrac{3}{5}\)e\(|4|=4=p\) e.
Portanto,
\[\begin{align*} r &= \dfrac{\left(\dfrac{3}{5}\right)(4)}{1+\dfrac{3}{5}\cos\theta} \\ r &= \dfrac{\dfrac{12}{5}}{1+\dfrac{3}{5}\cos\theta} \\ r &=\dfrac{\dfrac{12}{5}}{1\left(\dfrac{5}{5}\right)+\dfrac{3}{5}\cos\theta} \\ r &=\dfrac{\dfrac{12}{5}}{\dfrac{5}{5}+\dfrac{3}{5}\cos\theta} \\ r &= \dfrac{12}{5}⋅\dfrac{5}{5+3\cos\theta} \\ r &=\dfrac{12}{5+3\cos\theta} \end{align*}\]
Encontre a forma polar da cônica com foco na origem\(e=1\), e na diretriz\(x=−1\).
- Resposta
-
\(r=\dfrac{1}{1−\cos\theta}\)
Converta a forma cônica\(r=\dfrac{1}{5−5\sin \theta}\) em retangular.
Solução
Vamos reorganizar a fórmula para usar as identidades\(r=\sqrt{x^2+y^2}\)\(x=r \cos \theta\),\(y=r \sin \theta\) e.
\[\begin{align*} r&=\dfrac{1}{5-5 \sin \theta} \\ r\cdot (5-5 \sin \theta)&=\dfrac{1}{5-5 \sin \theta}\cdot (5-5 \sin \theta)\qquad \text{Eliminate the fraction.} \\ 5r-5r \sin \theta&=1 \qquad \text{Distribute.} \\ 5r&=1+5r \sin \theta \qquad \text{Isolate }5r. \\ 25r^2&={(1+5r \sin \theta)}^2 \qquad \text{Square both sides. } \\ 25(x^2+y^2)&={(1+5y)}^2 \qquad \text{Substitute } r=\sqrt{x^2+y^2} \text{ and }y=r \sin \theta. \\ 25x^2+25y^2&=1+10y+25y^2 \qquad \text{Distribute and use FOIL. } \\ 25x^2-10y&=1 \qquad \text{Rearrange terms and set equal to 1.} \end{align*}\]
Converta a forma cônica\(r=\dfrac{2}{1+2 \cos \theta}\) em retangular.
- Resposta
-
\(4−8x+3x^2−y^2=0\)
Acesse esses recursos on-line para obter instruções adicionais e praticar com cônicas em coordenadas polares.
- Equações polares de seções cônicas
- Representação gráfica de equações polares de cônicas - 1
- Representação gráfica de equações polares de cônicas - 2
Visite este site para obter mais perguntas práticas do Learningpod.
Conceitos-chave
- Qualquer cônica pode ser determinada por um único foco, a excentricidade correspondente e a diretriz. Também podemos definir uma cônica em termos de um ponto fixo, o foco\(P(r,\theta)\) no polo e uma linha, a diretriz, que é perpendicular ao eixo polar.
- Uma cônica é o conjunto de todos os pontos\(e=\dfrac{PF}{PD}\), onde a excentricidade\(e\) é um número real positivo. Cada cônica pode ser escrita em termos de sua equação polar. Veja o exemplo\(\PageIndex{1}\).
- As equações polares das cônicas podem ser representadas graficamente. Veja exemplo\(\PageIndex{2}\)\(\PageIndex{3}\), exemplo e exemplo\(\PageIndex{4}\).
- As cônicas podem ser definidas em termos de foco, diretriz e excentricidade. Veja o exemplo\(\PageIndex{5}\) e o exemplo\(\PageIndex{6}\).
- Podemos usar as identidades\(r=\sqrt{x^2+y^2}\),\(x=r \cos \theta\), e\(y=r \sin \theta\) para converter a equação de uma forma cônica da forma polar para a retangular. Veja o exemplo\(\PageIndex{7}\).


