4.3: Modelagem com funções lineares
- Page ID
- 189447
objetivos de aprendizagem
- Crie modelos lineares a partir de descrições verbais.
- Modele um conjunto de dados com uma função linear.
Emily é uma estudante universitária que planeja passar o verão em Seattle. Ela economizou $3.500 para sua viagem e prevê gastar $400 por semana em aluguel, alimentação e atividades. Como podemos escrever um modelo linear para representar a situação dela? O que seria o intercepto X e o que ela pode aprender com isso? Para responder a essas e outras perguntas relacionadas, podemos criar um modelo usando uma função linear. Modelos como esse podem ser extremamente úteis para analisar relacionamentos e fazer previsões com base nesses relacionamentos. Nesta seção, exploraremos exemplos de modelos de funções lineares.

Identificando etapas para modelar e resolver problemas
Ao modelar cenários com funções lineares e resolver problemas envolvendo quantidades com uma taxa de variação constante, normalmente seguimos as mesmas estratégias de problemas que usaríamos para qualquer tipo de função. Vamos analisá-los brevemente:
Identifique quantidades variáveis e, em seguida, defina variáveis descritivas para representar essas quantidades. Quando apropriado, desenhe uma imagem ou defina um sistema de coordenadas.
Leia atentamente o problema para identificar informações importantes. Procure informações que forneçam valores para as variáveis ou valores para partes do modelo funcional, como inclinação e valor inicial.
Leia atentamente o problema para determinar o que estamos tentando encontrar, identificar, resolver ou interpretar.
Identifique um caminho de solução desde as informações fornecidas até o que estamos tentando encontrar. Muitas vezes, isso envolve verificar e rastrear unidades, criar uma tabela ou até mesmo encontrar uma fórmula para a função que está sendo usada para modelar o problema.
Quando necessário, escreva uma fórmula para a função.
Resolva ou avalie a função usando a fórmula.
Reflita se sua resposta é razoável para a situação dada e se ela faz sentido matematicamente.
Transmita claramente seu resultado usando unidades apropriadas e responda em frases completas quando necessário.
Construindo modelos lineares
Agora vamos dar uma olhada no estudante em Seattle. Na situação dela, há duas quantidades variáveis: tempo e dinheiro. A quantidade de dinheiro restante para ela durante as férias depende de quanto tempo ela fica. Podemos usar essas informações para definir nossas variáveis, incluindo unidades.
- Produção:\(M\), dinheiro restante, em dólares
- Entrada:\(t\), tempo, em semanas
Portanto, a quantidade de dinheiro restante depende do número de semanas:\(M(t)\)
Também podemos identificar o valor inicial e a taxa de variação.
- Valor inicial: Ela economizou $3.500, então $3.500 é o valor inicial para M.
- Taxa de mudança: ela prevê gastar $400 por semana, então —$400 por semana é a taxa de mudança, ou inclinação.
Observe que a unidade de dólares por semana corresponde à unidade da nossa variável de saída dividida pela nossa variável de entrada. Além disso, como a inclinação é negativa, a função linear está diminuindo. Isso deve fazer sentido porque ela está gastando dinheiro toda semana.
A taxa de mudança é constante, então podemos começar com o modelo linear\(M(t)=mt+b\). Em seguida, podemos substituir o intercepto e a inclinação fornecidos.
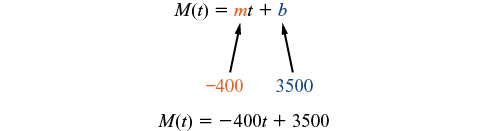
Para encontrar o intercepto x, definimos a saída como zero e resolvemos a entrada.
\[\begin{align*} 0&=−400t+3500 \\ t&=\dfrac{3500}{400} \\ &=8.75 \end{align*}\]
O intercepto X é de 8,75 semanas. Como isso representa o valor de entrada quando a saída for zero, podemos dizer que Emily não terá mais dinheiro após 8,75 semanas.
Ao modelar qualquer cenário da vida real com funções, normalmente há um domínio limitado sobre o qual esse modelo será válido — quase nenhuma tendência continua indefinidamente. Aqui, o domínio se refere ao número de semanas. Nesse caso, não faz sentido falar sobre valores de entrada menores que zero. Um valor de entrada negativo pode se referir a algumas semanas antes de ela economizar $3.500, mas o cenário discutido coloca a questão quando ela economizou $3.500, porque é quando sua viagem e os gastos subsequentes começam. Também é provável que esse modelo não seja válido após o intercepto x, a menos que Emily use um cartão de crédito e entre em dívida. O domínio representa o conjunto de valores de entrada, portanto, o domínio razoável para essa função é\(0{\leq}t{\leq}8.75\).
No exemplo acima, recebemos uma descrição por escrito da situação. Seguimos as etapas de modelagem de um problema para analisar as informações. No entanto, as informações fornecidas podem nem sempre ser as mesmas. Às vezes, podemos receber uma interceptação. Outras vezes, podemos receber um valor de saída. Devemos ter o cuidado de analisar as informações que recebemos e usá-las adequadamente para construir um modelo linear.
Usando um determinado intercepto para criar um modelo
Alguns problemas do mundo real fornecem o intercepto y, que é o valor constante ou inicial. Uma vez que o intercepto y é conhecido, o intercepto x pode ser calculado. Suponha, por exemplo, que Hannah planeje pagar um empréstimo sem juros de seus pais. O saldo do empréstimo dela é de $1.000. Ela planeja pagar $250 por mês até que seu saldo seja $0. O intercepto y é o valor inicial de sua dívida, ou $1.000. A taxa de variação, ou inclinação, é de -$250 por mês. Podemos então usar a forma de interceptação de inclinação e as informações fornecidas para desenvolver um modelo linear.
\[\begin{align*} f(x)&=mx+b \\ &=-250x+1000 \end{align*}\]
Agora podemos definir a função igual a 0 e resolver\(x\) para encontrar o intercepto x.
\[\begin{align*} 0&=-250+1000 \\ 1000&=250x \\ 4&=x \\ x&=4 \end{align*}\]
O intercepto x é o número de meses que ela leva para atingir um saldo de $0. O intercepto X é de 4 meses, então Hannah levará quatro meses para pagar seu empréstimo.
Usando uma determinada entrada e saída para criar um modelo
Muitos aplicativos do mundo real não são tão diretos quanto os que acabamos de considerar. Em vez disso, eles exigem que identifiquemos algum aspecto de uma função linear. Às vezes, podemos ser solicitados a avaliar o modelo linear em uma determinada entrada ou definir a equação do modelo linear igual a uma saída especificada.
![]() Dado um problema de palavras que inclui dois pares de valores de entrada e saída, use a função linear para resolver um problema.
Dado um problema de palavras que inclui dois pares de valores de entrada e saída, use a função linear para resolver um problema.
- Identifique os valores de entrada e saída.
- Converta os dados em dois pares de coordenadas.
- Encontre a inclinação.
- Escreva o modelo linear.
- Use o modelo para fazer uma previsão avaliando a função em um determinado valor x.
- Use o modelo para identificar um valor x que resulta em um determinado valor y.
- Responda à pergunta feita.
Exemplo\(\PageIndex{1}\): Using a Linear Model to Investigate a Town’s Population
A população de uma cidade vem crescendo linearmente. Em 2004, a população era de 6.200. Em 2009, a população havia crescido para 8.100. Suponha que essa tendência continue.
- Preveja a população em 2013.
- Identifique o ano em que a população chegará a 15.000.
Solução
As duas quantidades variáveis são o tamanho da população e o tempo. Embora pudéssemos usar o valor real do ano como a quantidade de entrada, isso tende a levar a equações muito complicadas porque o intercepto y corresponderia ao ano 0, há mais de 2000 anos!
Para tornar a computação um pouco mais agradável, definiremos nossa entrada como o número de anos desde 2004:
- Entrada:\(t\), anos desde 2004
- Saída:\(P(t)\), a população da cidade
Para prever a população em 2013 (\(t=9\)), primeiro precisaríamos de uma equação para a população. Da mesma forma, para descobrir quando a população chegaria a 15.000, precisaríamos resolver a entrada que forneceria uma produção de 15.000. Para escrever uma equação, precisamos do valor inicial e da taxa de variação ou inclinação.
Para determinar a taxa de variação, usaremos a mudança na saída por mudança na entrada.
\[m=\dfrac{\text{change in output}}{\text{change in input}}\]
O problema nos dá dois pares de entrada-saída. Convertendo-os para corresponder às nossas variáveis definidas, o ano de 2004 corresponderia\(t=0\), dando o ponto\((0,6200)\). Observe que, por meio de nossa escolha inteligente de definição de variável, “demos” a nós mesmos o intercepto y da função. O ano de 2009 corresponderia a\(t=5\), dando o ponto\((5,8100)\).
Os dois pares de coordenadas são\((0,6200)\)\((5,8100)\) e. Lembre-se de que encontramos exemplos nos quais nos foram fornecidos dois pontos anteriormente no capítulo. Podemos usar esses valores para calcular a inclinação.
\[\begin{align*} m&=\dfrac{8100-6200}{5-0}\\ &=\dfrac{1900}{5} \\ &=380 \text{ people per year} \end{align*}\]
Já conhecemos o intercepto y da linha, então podemos escrever imediatamente a equação:
\[P(t)=380t+6200\]
Para prever a população em 2013, avaliamos nossa função em\(t=9\).
\[\begin{align*} P(9)&=380(9)+6,200 \\ &=9,620 \end{align*}\]
Se a tendência continuar, nosso modelo prevê uma população de 9.620 em 2013.
Para descobrir quando a população chegará a 15.000, podemos definir\(P(t)=15000\) e resolver\(t\).
\[\begin{align*} 15000&=380t+6200 \\ 8800&=380t \\ t&{\approx}23.158 \end{align*}\]
Nosso modelo prevê que a população chegará a 15.000 em pouco mais de 23 anos após 2004, ou em algum lugar por volta do ano de 2027.
Exercício\(\PageIndex{1A}\)
Uma empresa vende donuts. Eles incorrem em um custo fixo de $25.000 para aluguel, seguro e outras despesas. A produção de cada donut custa $0,25.
- Escreva um modelo linear para representar o custo C da empresa em função do\(x\) número de donuts produzidos.
- Encontre e interprete o intercepto y.
Solução
a.\(C(x)=0.25x+25,000\) b. O intercepto y é\((0,25,000)\). Se a empresa não produzir uma única rosquinha, ela ainda terá um custo de $25.000.
Exercício\(\PageIndex{1B}\)
A população de uma cidade vem crescendo linearmente. Em 2008, a população era de 28.200. Em 2012, a população era de 36.800. Suponha que essa tendência continue.
- Preveja a população em 2014.
- Identifique o ano em que a população chegará a 54.000.
Solução
a. 41.100 b. 2020
Usando um diagrama para modelar um problema
É útil para muitos aplicativos do mundo real desenhar uma imagem para ter uma ideia de como as variáveis que representam a entrada e a saída podem ser usadas para responder a uma pergunta. Para desenhar a imagem, primeiro considere o que o problema está pedindo. Em seguida, determine a entrada e a saída. O diagrama deve relacionar as variáveis. Freqüentemente, formas ou figuras geométricas são desenhadas. As distâncias geralmente são traçadas. Se um triângulo reto for esboçado, o Teorema de Pitágoras relaciona os lados. Se um retângulo for esboçado, rotular a largura e a altura é útil.
Exemplo\(\PageIndex{2}\): Using a Diagram to Model Distance Walked
Anna e Emanuel começam no mesmo cruzamento. Anna caminha para o leste a 4 milhas por hora, enquanto Emanuel caminha para o sul a 3 milhas por hora. Eles estão se comunicando com um rádio bidirecional que tem um alcance de 2 milhas. Quanto tempo depois de começarem a andar, eles perderão o contato por rádio?
Solução
Em essência, podemos responder parcialmente a essa pergunta dizendo que eles perderão o contato por rádio quando estiverem a 3 km de distância, o que nos leva a fazer uma nova pergunta:
“Quanto tempo eles levarão para ficarem separados por 3 km?”
Nesse problema, nossas quantidades variáveis são tempo e posição, mas, em última análise, precisamos saber quanto tempo levará para que elas estejam separadas por 3 km. Podemos ver que o tempo será nossa variável de entrada, então definiremos nossas variáveis de entrada e saída.
- Entrada:\(t\), tempo em horas.
- Saída:\(A(t)\), distância em milhas e\(E(t)\), distância em milhas
Como não é óbvio como definir nossa variável de saída, começaremos desenhando uma imagem como Figura\(\PageIndex{3}\).
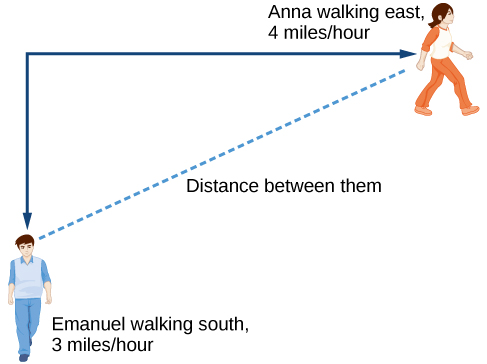
- Valor inicial: Ambos começam na mesma interseção, então\(t=0\), quando, a distância percorrida por cada pessoa também deve ser 0. Assim, o valor inicial para cada um é 0.
- Taxa de mudança: Anna está andando 4 milhas por hora e Emanuel está andando 3 milhas por hora, que são ambas taxas de mudança. A inclinação para\(A\) é 4 e a inclinação para\(E\) é 3.
Usando esses valores, podemos escrever fórmulas para a distância que cada pessoa percorreu.
\[A(t)=4t\]
\[E(t)=3t\]
Para esse problema, as distâncias do ponto de partida são importantes. Para anotá-los, podemos definir um sistema de coordenadas, identificando o “ponto de partida” na interseção onde ambos começaram. Em seguida, podemos usar a variável\(A\), que introduzimos acima, para representar a posição de Anna e defini-la como uma medida do ponto de partida na direção leste. Da mesma forma, pode usar a variável,\(E\), para representar a posição de Emanuel, medida a partir do ponto de partida na direção sul. Observe que, ao definir o sistema de coordenadas, especificamos o ponto inicial da medição e a direção da medida.
Podemos então definir uma terceira variável,\(D\), para ser a medida da distância entre Anna e Emanuel. Mostrar as variáveis no diagrama geralmente é útil, como podemos ver na Figura\(\PageIndex{4}\).
Lembre-se de que precisamos saber quanto tempo leva\(D\), a distância entre eles, para ser igual a 2 milhas. Observe que, para qualquer entrada dada\(t\), as saídas\(A(t)\) e\(D(t)\) representam distâncias.\(E(t)\)
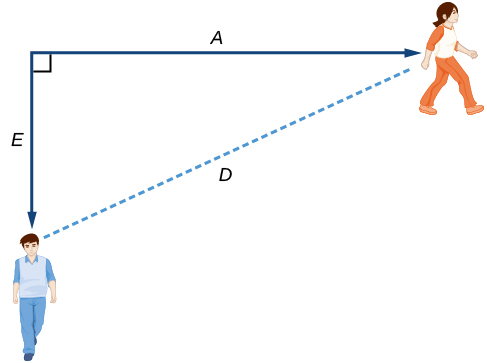
Usando o Teorema de Pitágoras, obtemos:
\[\begin{align*} d(t)^2&=A(t)^2+E(t)^2 \\ &=(4t)^2+(3t)^2 \\ &=16t^2+9t^2 \\ &=25t^2 \\ D(t)&=\pm\sqrt{25t^2} &\text{Solve for $D(t)$ using the square root} \\ &= \pm 5|t| \end{align*}\]
Nesse cenário, estamos considerando apenas valores positivos de\(t\), então nossa distância sempre\(D(t)\) será positiva. Podemos simplificar essa resposta para\(D(t)=5t\). Isso significa que a distância entre Anna e Emanuel também é uma função linear. Como D é uma função linear, agora podemos responder à pergunta de quando a distância entre elas chegará a 2 milhas. Definiremos a saída\(D(t)=2\) e resolveremos\(t\).
\[\begin{align*} D(t)&=2 \\ 5t&=2 \\ t&=\dfrac{2}{5}=0.4 \end{align*}\]
Eles sairão do contato por rádio em 0,4 horas ou 24 minutos.
![]() Devo desenhar diagramas quando recebo informações com base em uma forma geométrica?
Devo desenhar diagramas quando recebo informações com base em uma forma geométrica?
Sim. Desenhe a figura e rotule as quantidades e incógnitas no esboço.
Exemplo\(\PageIndex{3}\): Using a Diagram to Model Distance between Cities
Há uma estrada reta que vai da cidade de Westborough até Agritown 30 milhas a leste e 10 milhas ao norte. No meio desta estrada, ela se cruza com uma segunda estrada, perpendicular à primeira, que leva à cidade de Eastborough. Se a cidade de Eastborough estiver localizada a 20 milhas diretamente a leste da cidade de Westborough, a que distância fica o entroncamento rodoviário de Westborough?
Solução
Aqui, pode ser útil fazer um retrato da situação. Veja a Figura\(\PageIndex{5}\). Seria então útil introduzir um sistema de coordenadas. Embora possamos colocar a origem em qualquer lugar, colocá-la em Westborough parece conveniente. Isso coloca Agritown nas coordenadas\((30, 10)\), e Eastborough em\((20,0)\).
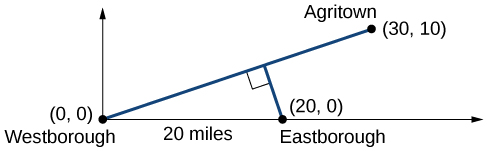
Usando esse ponto junto com a origem, podemos encontrar a inclinação da linha de Westborough a Agritown:
\[m=\dfrac{10-0}{30-0}=\dfrac{1}{3}\]
A equação da estrada de Westborough a Agritown seria
\[W(x)=\dfrac{1}{3}x\]
A partir disso, podemos determinar que a estrada perpendicular para Eastborough terá inclinação\(m=–3\). Como a cidade de Eastborough está no ponto\((20, 0)\), podemos encontrar a equação:
\[\begin{align*} E(x)&=−3x+b \\ 0&=−3(20)+b &\text{Substitute in $(20, 0)$} \\ b&=60 \\ E(x)&=−3x+60 \end{align*}\]
Agora podemos encontrar as coordenadas da junção das estradas encontrando a interseção dessas linhas. Definindo-os iguais,
\[\begin{align*} \dfrac{1}{3}x&=−3x+60 \\ \dfrac{10}{3}x&=60 \\ 10x&=180 \\ x&=18 &\text{Substituting this back into $W(x)$} \\ y&=W(18) \\ &= \dfrac{1}{3}(18) \\&=6 \end{align*}\]
As estradas se cruzam no ponto\((18,6)\). Usando a fórmula da distância, agora podemos encontrar a distância de Westborough até a junção.
\[\begin{align*} \text{distance}&=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \\ &=\sqrt{(18-0)^2+(6-0)^2} \\ &\approx 18.743 \text{miles} \end{align*}\]
Análise
Um bom uso dos modelos lineares é aproveitar o fato de que os gráficos dessas funções são linhas. Isso significa que aplicativos do mundo real que discutem mapas precisam de funções lineares para modelar as distâncias entre os pontos de referência.
Exercício\(\PageIndex{2}\)
Há uma estrada reta que vai da cidade de Timpson até Ashburn 60 milhas a leste e 12 milhas ao norte. No meio da estrada, ele se cruza com uma segunda estrada, perpendicular à primeira, levando à cidade de Garrison. Se a cidade de Garrison estiver localizada 22 milhas diretamente a leste da cidade de Timpson, a que distância fica o entroncamento rodoviário de Timpson?
Solução
21,15 milhas
Construindo sistemas de modelos lineares
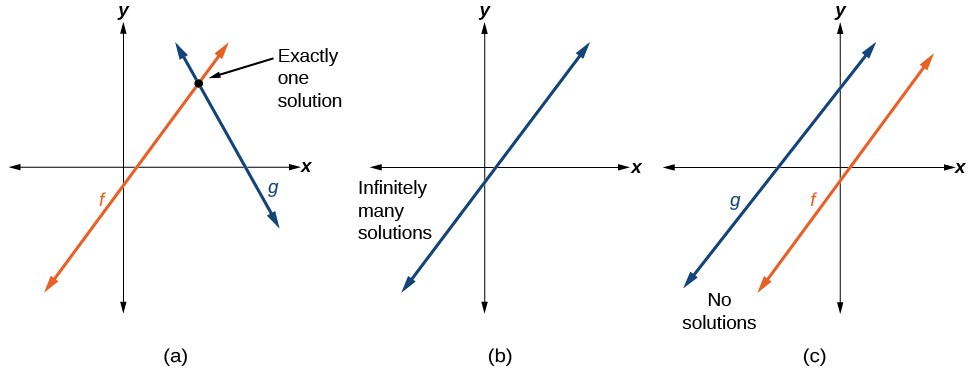
Situações do mundo real, incluindo duas ou mais funções lineares, podem ser modeladas com um sistema de equações lineares. Lembre-se de que, ao resolver um sistema de equações lineares, estamos procurando pontos que as duas retas têm em comum. Normalmente, existem três tipos de respostas possíveis, conforme mostrado na Figura\(\PageIndex{6}\).
![]() Dada uma situação que represente um sistema de equações lineares, escreva o sistema de equações e identifique a solução.
Dada uma situação que represente um sistema de equações lineares, escreva o sistema de equações e identifique a solução.
- Identifique a entrada e a saída de cada modelo linear.
- Identifique a inclinação e o intercepto y de cada modelo linear.
- Encontre a solução definindo as duas funções lineares iguais a outra e resolvendo para\(x\), ou encontre o ponto de interseção em um gráfico.
Exemplo\(\PageIndex{4}\): Building a System of Linear Models to Choose a Truck Rental Company
Jamal está escolhendo entre duas locadoras de caminhões. A primeira, a Keep on Trucking, Inc., cobra uma taxa inicial de $20, depois 59 centavos por milha [1]. O segundo, Move It Your Way, cobra uma taxa inicial de $16, depois 63 centavos por milha. Quando a Keep on Trucking, Inc. será a melhor escolha para Jamal?
Solução
As duas quantidades importantes desse problema são o custo e o número de milhas percorridas. Como temos duas empresas a considerar, definiremos duas funções.
- Entrada:\(d\), distância percorrida em milhas
- Saídas:\(K(d):\) custo, em dólares, para alugar na Keep on Trucking
\(M(d):\)custo, em dólares, para alugar na Move It Your Way
- Valor inicial: taxa inicial:\(K(0)=20\) e\(M(0)=16\)
- Taxa de variação:\(K(d)=\dfrac{$0.59}{\text{mile}}\) e\(P(d)=\dfrac{$0.63}{\text{mile}}\)
Uma função linear tem a forma\(f(x)=mx+b\). Usando as taxas de variação e as cobranças iniciais, podemos escrever as equações
\[K(d)=0.59d+20 \nonumber\]
\[M(d)=0.63d+16 \nonumber\]
Usando essas equações, podemos determinar quando a Keep on Trucking, Inc. será a melhor escolha. Como tudo o que precisamos tomar essa decisão são os custos, estamos procurando quando a Keep on Trucking, Inc. custará menos ou quando\(K(d)<M(d)\). O caminho da solução nos levará a encontrar as equações para as duas funções, encontrar a interseção e, em seguida, ver onde a\(K(d)\) função é menor.
Esses gráficos são esboçados na Figura\(\PageIndex{7}\), com\(K(d)\) em azul.
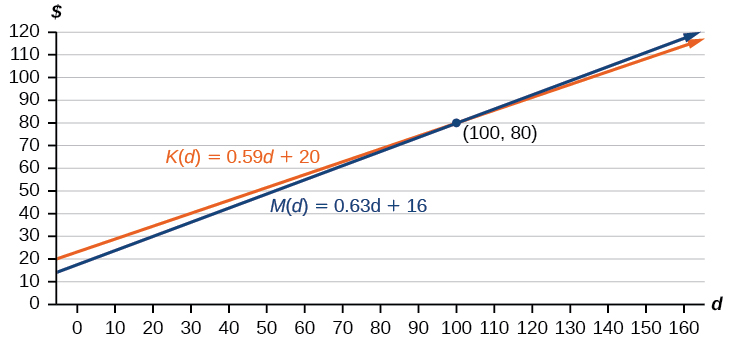
Para encontrar a interseção, definimos as equações iguais e resolvemos:
\[\begin{align*} K(d)&=M(d) \\ 0.59d+20&=0.63d+16 \\ 4&=0.04d \\ 100&=d \\ d&=100 \end{align*}\]
Isso nos diz que o custo das duas empresas será o mesmo se 100 milhas forem percorridas. Olhando o gráfico ou observando que\(K(d)\) está crescendo a uma taxa mais lenta, podemos concluir que a Keep on Trucking, Inc. será o preço mais barato quando mais de 100 milhas forem percorridas, ou seja\(d>100\).
Conceitos chave
- Podemos usar as mesmas estratégias de problemas que usaríamos para qualquer tipo de função.
- Ao modelar e resolver um problema, identifique as variáveis e procure os valores-chave, incluindo a inclinação e o intercepto y.
- Desenhe um diagrama, quando apropriado.
- Verifique a razoabilidade da resposta.
- Modelos lineares podem ser construídos identificando ou calculando a inclinação e usando o intercepto y.
- O intercepto x pode ser encontrado pela configuração\(y=0\), que é definir a expressão\(mx+b\) igual a 0.
- O ponto de interseção de um sistema de equações lineares é o ponto em que os valores x e y são iguais.
- Um gráfico do sistema pode ser usado para identificar os pontos em que uma linha fica abaixo (ou acima) da outra linha.
Notas de pé
1 Tarifas recuperadas em 2 de agosto de 2010 em www.budgettruck.com e http://www.uhaul.com/


