12.2: Entropia

Objetivos de

• Definir entropia
• Explicar a relação entre a entropia e o número de microestados
• Preveja o sinal da mudança de entropia para processos químicos e físicos

Em 1824, aos 28 anos, Nicolas Léonard Sadi Carnot (Figura\(\PageIndex{2}\)) publicou os resultados de um extenso estudo sobre a eficiência dos motores térmicos a vapor. Em uma revisão posterior das descobertas de Carnot, Rudolf Clausius introduziu uma nova propriedade termodinâmica que relaciona o fluxo de calor espontâneo que acompanha um processo com a temperatura na qual o processo ocorre. Essa nova propriedade foi expressa como a razão entre o calor reversível (q _rev) e a temperatura kelvin (T). O termo processo reversível se refere a um processo que ocorre em uma taxa tão lenta que está sempre em equilíbrio e sua direção pode ser alterada (pode ser “revertida”) por uma mudança infinitesimalmente pequena em alguma condição. Observe que a ideia de um processo reversível é um formalismo necessário para apoiar o desenvolvimento de vários conceitos termodinâmicos; nenhum processo real é verdadeiramente reversível, mas sim classificado como irreversível.

Figura\(\PageIndex{1}\): (a) A pesquisa de Nicholas Léonard Sadi Carnot sobre máquinas movidas a vapor e (b) o estudo posterior de Rudolf Clausius sobre essas descobertas levaram a descobertas inovadoras sobre processos espontâneos de fluxo de calor.

Semelhante a outras propriedades termodinâmicas, essa nova quantidade é uma função de estado e, portanto, sua mudança depende apenas dos estados inicial e final de um sistema. Em 1865, Clausius chamou essa propriedade de entropia (S) e definiu sua mudança para qualquer processo da seguinte forma:

\[ΔS=\dfrac{q_\ce{rev}}{T} \label{Eq1} \]

A mudança de entropia para um processo real e irreversível é então igual à do processo teórico reversível que envolve os mesmos estados inicial e final.

Entropia e microestados

Seguindo o trabalho de Carnot e Clausius, Ludwig Boltzmann desenvolveu um modelo estatístico em escala molecular que relacionou a entropia de um sistema ao número de microestados possíveis para o sistema. Um microestado (\(\Omega\))é uma configuração específica das localizações e energias dos átomos ou moléculas que compõem um sistema como o seguinte:

\[S=k \ln \Omega \label{Eq2} \]

Aqui k é a constante de Boltzmann e tem um valor de\(1.38 \times 10^{−23}\, J/K\).

Quanto às outras funções de estado, a mudança na entropia de um processo é a diferença entre seus valores finais (S _f) e iniciais (S _i):

\[\begin{align} ΔS &=S_\ce{f}−S_\ce{i} \nonumber \\[4pt] &=k \ln \Omega_\ce{f} − k \ln \Omega_\ce{i} \nonumber \\[4pt] &=k \ln\dfrac{\Omega_\ce{f}}{\Omega_\ce{i}} \label{Eq2a} \end{align} \]

Para processos que envolvem um aumento no número de microestados do sistema\(\Omega_f > \Omega_i\), a entropia do sistema aumenta,\(ΔS > 0\). Por outro lado, processos que reduzem o número de microestados no sistema,\(\Omega_f < \Omega_i\), produzem uma diminuição na entropia do sistema,\(ΔS < 0\). Essa interpretação da entropia em escala molecular fornece um link para a probabilidade de que um processo ocorra, conforme ilustrado nos próximos parágrafos.

Figura\(\PageIndex{2}\): Os dezesseis microestados associados à colocação de quatro partículas em duas caixas são mostrados. Os microestados são coletados em cinco distribuições — (a), (b), (c), (d) e (e) — com base no número de partículas em cada caixa.

Cinco linhas de diagramas que parecem dominós são mostradas e rotuladas como a, b, c, d e e. A linha a tem um “dominó” com quatro pontos no lado esquerdo, vermelho, verde, azul e amarelo em um padrão no sentido horário a partir do canto superior esquerdo e nenhum ponto no direito. A linha b tem quatro “dominós”, cada um com três pontos à esquerda e um ponto à direita. O primeiro mostra um “dominó” com verde, amarelo e azul à esquerda e vermelho à direita. O segundo “dominó” tem amarelo, azul e vermelho à esquerda e verde à direita. O terceiro “dominó” tem vermelho, verde e amarelo à esquerda e azul à direita, enquanto o quarto tem vermelho, verde e azul à esquerda e amarelo à direita. A linha c tem seis “dominós”, cada um com dois pontos em cada lado. O primeiro tem um vermelho e verde à esquerda e um azul e amarelo à direita. O segundo tem vermelho e azul à esquerda e verde e amarelo à direita, enquanto o terceiro tem amarelo e vermelho à esquerda e verde e azul à direita. O quarto tem um verde e azul à esquerda e um vermelho e amarelo à direita. O quinto tem um verde e amarelo à esquerda e um vermelho e azul à direita. O sexto tem um azul e amarelo à esquerda e um verde e vermelho à direita. A linha d tem quatro “dominós”, cada um com um ponto à esquerda e três à direita. O primeiro “dominó” tem vermelho à esquerda e azul, verde e amarelo à direita. O segundo tem um verde à esquerda e um vermelho, amarelo e azul à direita. O terceiro tem um azul à esquerda e um vermelho, verde e amarelo à direita. O quarto tem um amarelo à esquerda e um vermelho, verde e azul à direita. A linha e tem 1 “dominó” sem pontos à esquerda e quatro pontos à direita que são vermelhos, verdes, azuis e amarelos.

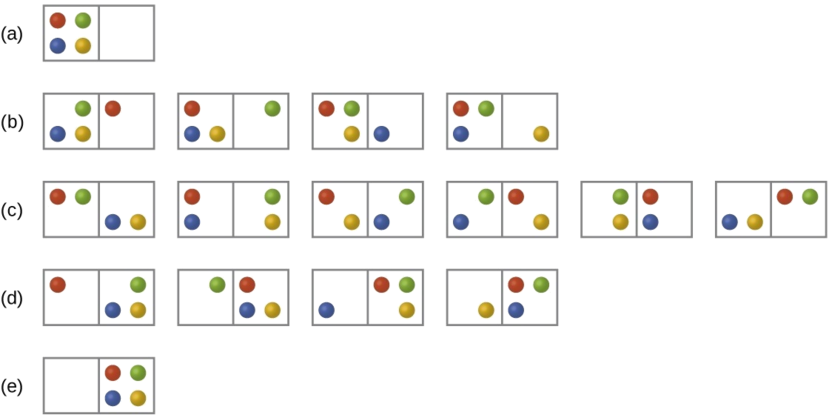
Considere o caso geral de um sistema composto por N partículas distribuídas entre n caixas. O número de microestados possíveis para esse sistema é ^{n N.} Por exemplo, distribuir quatro partículas entre duas caixas resultará em 2 ⁴ = 16 microestados diferentes, conforme ilustrado na Figura\(\PageIndex{2}\). Microestados com arranjos de partículas equivalentes (sem considerar identidades individuais de partículas) são agrupados e chamados de distribuições (às vezes chamados de macroestados ou configurações). A probabilidade de um sistema existir com seus componentes em uma determinada distribuição é proporcional ao número de microestados dentro da distribuição. Como a entropia aumenta logaritmicamente com o número de microestados, a distribuição mais provável é, portanto, a de maior entropia.

Para esse sistema, a configuração mais provável é um dos seis microestados associados à distribuição (c), onde as partículas são distribuídas uniformemente entre as caixas, ou seja, uma configuração de duas partículas em cada caixa. A probabilidade de encontrar o sistema nessa configuração é

 

\[\dfrac{6}{16} = \dfrac{3}{8} \nonumber \]

A configuração menos provável do sistema é aquela em que todas as quatro partículas estão em uma caixa, correspondendo às distribuições (a) e (e), cada uma com uma probabilidade de

\[\dfrac{1}{16} \nonumber \]

A probabilidade de encontrar todas as partículas em apenas uma caixa (seja a caixa esquerda ou a caixa direita) é então

\[\left(\dfrac{1}{16}+\dfrac{1}{16}\right)=\dfrac{2}{16} = \dfrac{1}{8} \nonumber \]

 

À medida que você adiciona mais partículas ao sistema, o número de microestados possíveis aumenta exponencialmente (2 ^N). Um sistema macroscópico (do tamanho de um laboratório) normalmente consistiria em moles de partículas (N ~ 10 ²³), e o número correspondente de microestados seria incrivelmente grande. No entanto, independentemente do número de partículas no sistema, as distribuições nas quais números aproximadamente iguais de partículas são encontrados em cada caixa são sempre as configurações mais prováveis.

A distribuição mais provável é, portanto, a de maior entropia.

A descrição anterior de um gás ideal se expandindo para o vácuo é um exemplo macroscópico desse modelo de partícula em uma caixa. Para esse sistema, confirma-se que a distribuição mais provável é aquela em que a matéria está mais uniformemente dispersa ou distribuída entre os dois frascos. O processo espontâneo pelo qual o gás contido inicialmente em um frasco se expande para encher os dois frascos igualmente, portanto, produz um aumento na entropia para o sistema.

Figura\(\PageIndex{3}\): Isso mostra um modelo de microestado descrevendo o fluxo de calor de um objeto quente para um objeto frio. (a) Antes que o fluxo de calor ocorra, o objeto composto pelas partículas A e B contém ambas as unidades de energia e é representado por uma distribuição de três microestados. (b) Se o fluxo de calor resultar em uma dispersão uniforme da energia (uma unidade de energia transferida), resulta em uma distribuição de quatro microestados. (c) Se ambas as unidades de energia forem transferidas, a distribuição resultante terá três microestados.

Três linhas rotuladas a, b e c são mostradas e cada uma contém retângulos com dois lados, onde o lado esquerdo é rotulado como “A” e “B”, e o direito é rotulado como “C” e “D.” A linha a tem três retângulos, onde o primeiro tem um ponto acima e abaixo da letra A, o segundo tem um ponto acima de A e B e o terceiro tem um ponto acima e abaixo da letra B. A linha b tem quatro retângulos; o primeiro tem um ponto acima de A e C, o segundo tem um ponto acima de A e D, o terceiro tem um ponto acima de B e C e a quarta tem um ponto acima de B e D. A linha c tem três retângulos; a primeira tem um ponto acima e abaixo da letra C, a segunda tem um ponto acima de C e D e a terceira tem um ponto acima e abaixo da letra D.

Uma abordagem semelhante pode ser usada para descrever o fluxo espontâneo de calor. Considere um sistema composto por dois objetos, cada um contendo duas partículas e duas unidades de energia (representadas como “*”) na Figura\(\PageIndex{3}\). O objeto quente é composto pelas partículas A e B e inicialmente contém as duas unidades de energia. O objeto frio é composto por partículas C e D, que inicialmente não têm unidades de energia. A distribuição (a) mostra os três microestados possíveis para o estado inicial do sistema, com ambas as unidades de energia contidas no objeto quente. Se uma das duas unidades de energia for transferida, o resultado será a distribuição (b) consistindo em quatro microestados. Se ambas as unidades de energia forem transferidas, o resultado será uma distribuição (c) que consiste em três microestados. Assim, podemos descrever esse sistema por um total de dez microestados. A probabilidade de o calor não fluir quando os dois objetos são colocados em contato, ou seja, que o sistema permaneça na distribuição (a), é\(\frac{3}{10}\). O mais provável é que o fluxo de calor produza uma das outras duas distribuições, sendo a probabilidade combinada\(\frac{7}{10}\). O resultado mais provável é o fluxo de calor para produzir a dispersão uniforme da energia representada pela distribuição (b), sendo a probabilidade dessa configuração\(\frac{4}{10}\). Quanto ao exemplo anterior de dispersão de matéria, extrapolar esse tratamento para coleções macroscópicas de partículas aumenta dramaticamente a probabilidade da distribuição uniforme em relação às outras distribuições. Isso apóia a observação comum de que colocar objetos quentes e frios em contato resulta em um fluxo de calor espontâneo que, em última análise, equaliza as temperaturas dos objetos. E, novamente, esse processo espontâneo também é caracterizado por um aumento na entropia do sistema.

Exemplo\(\PageIndex{1}\): Determination of ΔS

Considere o sistema mostrado aqui. Qual é a mudança na entropia de um processo que converte o sistema de distribuição (a) para (c)?

 

Um diagrama mostra um retângulo com dois lados que tem quatro pontos, vermelho, verde, amarelo e azul escrito no lado esquerdo. Uma seta voltada para a direita leva a mais seis retângulos de dois lados, cada um com dois pontos nos lados esquerdo e direito. O primeiro retângulo tem um ponto vermelho e verde à esquerda e um azul e amarelo à direita, enquanto o segundo mostra um vermelho e azul à esquerda e um verde e amarelo à direita. O terceiro retângulo tem um ponto vermelho e amarelo à esquerda e um azul e verde à direita, enquanto o quarto mostra um verde e azul à esquerda e um vermelho e amarelo à direita. O quinto retângulo tem um ponto amarelo e verde à esquerda e um azul e vermelho à direita, enquanto o sexto mostra um amarelo e azul à esquerda e um verde e vermelho à direita.

Solução

Estamos interessados na seguinte mudança:

O número inicial de microestados é um, os seis finais:

\[\begin{align} ΔS &=k \ln\dfrac{\Omega_\ce{c}}{\Omega_\ce{a}} \nonumber \\[4pt] &= 1.38×10^{−23}\:J/K × \ln\dfrac{6}{1} \nonumber \\[4pt] &= 2.47×10^{−23}\:J/K \nonumber \end{align} \nonumber \]

O sinal desse resultado é consistente com a expectativa; como há mais microestados possíveis para o estado final do que para o estado inicial, a mudança na entropia deve ser positiva.

Exercício\(\PageIndex{1}\)

Considere o sistema mostrado na Figura\(\PageIndex{3}\). Qual é a mudança na entropia do processo em que toda a energia é transferida do objeto quente (AB) para o objeto frio (CD)?

Resposta

0 KG/KG

Prevendo o sinal de ΔS

As relações entre entropia, microestados e dispersão de matéria/energia descritas anteriormente nos permitem fazer generalizações sobre as entropias relativas das substâncias e prever o sinal de mudanças de entropia para processos químicos e físicos. Considere as mudanças de fase ilustradas na Figura\(\PageIndex{4}\). Na fase sólida, os átomos ou moléculas são restritos a posições quase fixas em relação uns aos outros e são capazes de oscilações apenas modestas em relação a essas posições. Com localizações essencialmente fixas para as partículas componentes do sistema, o número de microestados é relativamente pequeno. Na fase líquida, os átomos ou moléculas são livres para se mover uns sobre os outros, embora permaneçam relativamente próximos uns dos outros. Essa maior liberdade de movimento resulta em uma maior variação nas possíveis localizações das partículas, portanto, o número de microestados é correspondentemente maior do que o do sólido. Como resultado, S _líquido > S _sólido e o processo de conversão de uma substância de sólido em líquido (fusão) são caracterizados por um aumento na entropia, ΔS > 0. Pela mesma lógica, o processo recíproco (congelamento) exibe uma diminuição na entropia, ΔS < 0.

Figura\(\PageIndex{4}\): A entropia de uma substância aumenta (ΔS > 0) à medida que ela se transforma de um sólido relativamente ordenado em um líquido menos ordenado e depois em um gás ainda menos ordenado. A entropia diminui (ΔS < 0) à medida que a substância se transforma de um gás em um líquido e depois em um sólido.

Três frascos com tampa são mostrados com setas voltadas para a direita e para a esquerda entre cada um; o primeiro é rotulado acima como “delta S maior que 0” e abaixo como “delta S menor que 0”, enquanto o segundo é rotulado acima como “delta S maior que 0” e abaixo como “delta S menor que 0”. Uma seta longa voltada para a direita é desenhada acima de todos os frascos e rotulada como “Aumentando a entropia”. O frasco esquerdo contém vinte e sete partículas dispostas em um cubo no fundo do frasco e é rotulado como “Sólido cristalino” abaixo. O frasco do meio contém vinte e sete partículas dispersas aleatoriamente no fundo do frasco e é rotulado como “Líquido” abaixo. O frasco direito contém vinte e sete partículas dispersas dentro do frasco e se movendo rapidamente e é rotulado como “Gás” abaixo.

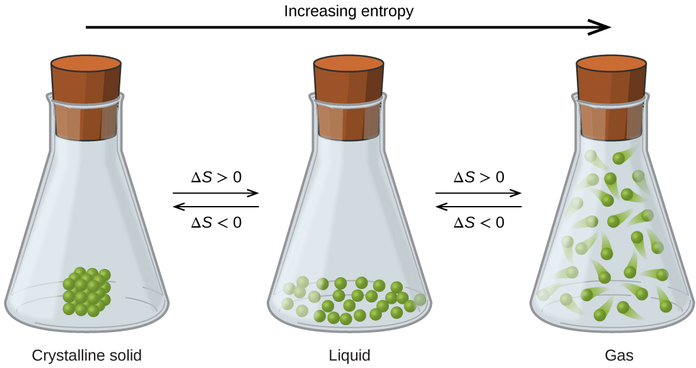
Agora, considere a fase de vapor ou gás. Os átomos ou moléculas ocupam um volume muito maior do que na fase líquida; portanto, cada átomo ou molécula pode ser encontrado em muito mais locais do que na fase líquida (ou sólida). Consequentemente, para qualquer substância, _gás S > S _líquido > S _sólido e os processos de vaporização e sublimação também envolvem aumentos na entropia, ΔS > 0. Da mesma forma, as transições de fase recíprocas, condensação e deposição, envolvem diminuições na entropia, ΔS < 0.

De acordo com a teoria cinético-molecular, a temperatura de uma substância é proporcional à energia cinética média de suas partículas. Aumentar a temperatura de uma substância resultará em vibrações mais extensas das partículas nos sólidos e traduções mais rápidas das partículas em líquidos e gases. Em temperaturas mais altas, a distribuição das energias cinéticas entre os átomos ou moléculas da substância também é mais ampla (mais dispersa) do que em temperaturas mais baixas. Assim, a entropia de qualquer substância aumenta com a temperatura (Figura\(\PageIndex{5}\)).

Figura\(\PageIndex{5}\): A entropia aumenta à medida que a temperatura de uma substância aumenta, o que corresponde à maior disseminação das energias cinéticas. Quando uma substância derrete ou se vaporiza, ela experimenta um aumento significativo na entropia.

Dois gráficos são mostrados. O eixo y do gráfico esquerdo é rotulado como “Fração de moléculas”, enquanto o eixo x é rotulado como “Velocidade, v (m/s)” e tem valores de 0 a 1.500 ao longo do eixo com incrementos de 500. Quatro linhas são traçadas neste gráfico. O primeiro, rotulado como “100 K”, atinge o pico em torno de 200 m/s, enquanto o segundo, denominado “200 K”, atinge o pico próximo a 300 m/s e é um pouco mais baixo no eixo y do que o primeiro. A terceira linha, chamada “500 K”, atinge o pico em torno de 550 m/s e é menor do que as duas primeiras no eixo y. A quarta linha, chamada “1000 K”, atinge o pico em torno de 750 m/s e é a mais baixa das quatro no eixo y. Cada linha fica cada vez mais ampla. O segundo gráfico tem um eixo y chamado “Entropia, S”, com uma seta voltada para cima e um eixo x rotulado como “Temperatura (K)” e uma seta voltada para a direita. O gráfico tem três colunas igualmente espaçadas no fundo, denominadas “Sólido”, “Líquido” e “Gás”, da esquerda para a direita. Uma linha se estende ligeiramente para cima através da primeira coluna em uma direção ligeiramente ascendente e, em seguida, vai direto para cima na transição entre as duas primeiras colunas. Em seguida, progride em uma leve direção ascendente através da segunda coluna, depois sobe dramaticamente entre a segunda e a terceira colunas, depois continua em uma direção ligeiramente ascendente mais uma vez. A primeira região vertical dessa linha é rotulada como “Fusão” e a segunda é chamada de “Ebulição”.

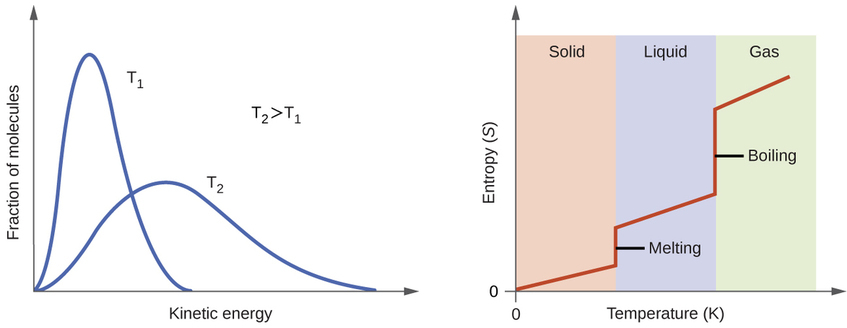
A entropia de uma substância é influenciada pela estrutura das partículas (átomos ou moléculas) que compõem a substância. Com relação às substâncias atômicas, os átomos mais pesados possuem maior entropia em uma determinada temperatura do que os átomos mais leves, o que é uma consequência da relação entre a massa de uma partícula e o espaçamento dos níveis quantizados de energia translacional (que é um tópico além do escopo de nosso tratamento). Para moléculas, um número maior de átomos (independentemente de suas massas) aumenta as formas pelas quais as moléculas podem vibrar e, portanto, o número de microestados possíveis e a entropia do sistema.

Finalmente, variações nos tipos de partículas afetam a entropia de um sistema. Em comparação com uma substância pura, na qual todas as partículas são idênticas, a entropia de uma mistura de dois ou mais tipos diferentes de partículas é maior. Isso se deve às orientações e interações adicionais que são possíveis em um sistema composto por componentes não idênticos. Por exemplo, quando um sólido se dissolve em um líquido, as partículas do sólido experimentam uma maior liberdade de movimento e interações adicionais com as partículas do solvente. Isso corresponde a uma dispersão mais uniforme de matéria e energia e a um maior número de microestados. O processo de dissolução, portanto, envolve um aumento na entropia, ΔS > 0.

Considerar os vários fatores que afetam a entropia nos permite fazer previsões informadas do sinal de ΔS para vários processos químicos e físicos, conforme ilustrado no Exemplo.

Exemplo\(\PageIndex{2}\): Predicting the Sign of ∆S

Preveja o sinal da mudança de entropia para os seguintes processos. Indique o motivo de cada uma de suas previsões.

1. Um mol de água líquida à temperatura ambiente\(⟶\) um mol de água líquida a 50 °C
2. \(\ce{Ag+}(aq)+\ce{Cl-}(aq)⟶\ce{AgCl}(s)\)
3. \(\ce{C6H6}(l)+\dfrac{15}{2}\ce{O2}(g)⟶\ce{6CO2}(g)+\ce{3H2O}(l)\)
4. \(\ce{NH3}(s)⟶\ce{NH3}(l)\)

Solução SS

1. positivo, aumentos de temperatura
2. negativo, redução no número de íons (partículas) em solução, diminuição da dispersão da matéria
3. diminuição líquida negativa na quantidade de espécies gasosas
4. positivo, transição de fase do sólido para o líquido, aumento líquido na dispersão da matéria

Exercício\(\PageIndex{2}\)

Preveja o sinal da mudança de entalpia para os seguintes processos. Dê um motivo para sua previsão.

1. \(\ce{NaNO3}(s)⟶\ce{Na+}(aq)+\ce{NO3-}(aq)\)
2. o congelamento de água líquida
3. \(\ce{CO2}(s)⟶\ce{CO2}(g)\)
4. \(\ce{CaCO}(s)⟶\ce{CaO}(s)+\ce{CO2}(g)\)

Responda a um

Positivo; O sólido se dissolve para dar um aumento de íons móveis na solução.

Resposta b

Negativo; O líquido se torna um sólido mais ordenado.

Resposta c

Positivo; O sólido relativamente ordenado se torna um gás

Resposta d

Positivo; Há uma produção líquida de um mol de gás.

Resumo

Entropia (\(S\)) é uma função de estado que pode estar relacionada ao número de microestados de um sistema (o número de maneiras pelas quais o sistema pode ser organizado) e à razão entre o calor reversível e a temperatura em Kelvin. Pode ser interpretado como uma medida da dispersão ou distribuição de matéria e/ou energia em um sistema e é frequentemente descrito como representando a “desordem” do sistema. Para uma determinada substância,\(S_{solid} < S_{liquid} \ll S_{gas}\) em um determinado estado físico a uma determinada temperatura, a entropia é tipicamente maior para átomos mais pesados ou moléculas mais complexas. A entropia aumenta quando um sistema é aquecido e quando as soluções se formam. Usando essas diretrizes, o sinal de mudanças de entropia para algumas reações químicas pode ser previsto de forma confiável.

Equações-chave

• \(ΔS=\dfrac{q_\ce{rev}}{T}\)
• S = k em W
• \(ΔS=k\ln\dfrac{W_\ce{f}}{W_\ce{i}}\)

Glossário

entropia (S)

função de estado que é uma medida da dispersão de matéria e/ou energia dentro de um sistema, determinada pelo número de microestados do sistema frequentemente descritos como uma medida da desordem do sistema

microestado (W)

possível configuração ou disposição de matéria e energia dentro de um sistema

processo reversível

processo que ocorre tão lentamente que é capaz de reverter a direção em resposta a uma mudança infinitesimalmente pequena nas condições; construção hipotética que só pode ser aproximada por processos reais removidos