3.4: Composição das funções

Objetivos de

• Combine funções usando operações algébricas.
• Crie uma nova função pela composição das funções.
• Avalie funções compostas.
• Encontre o domínio de uma função composta.
• Decomponha uma função composta em suas funções componentes.

Suponha que desejemos calcular quanto custa aquecer uma casa em um determinado dia do ano. O custo do aquecimento de uma casa dependerá da temperatura média diária e, por sua vez, a temperatura média diária depende do dia específico do ano. Observe como acabamos de definir duas relações: o custo depende da temperatura e a temperatura depende do dia.

Usando variáveis descritivas, podemos anotar essas duas funções. A função$C(T)$ fornece o custo$C$ do aquecimento de uma casa para uma determinada temperatura média diária em$T$ graus Celsius. A função$T(d)$ fornece a temperatura média diária no dia d do ano. Para qualquer dia,$Cost=C(T(d))$ significa que o custo depende da temperatura, que por sua vez depende do dia do ano. Assim, podemos avaliar a função de custo na temperatura$T(d)$. Por exemplo, poderíamos avaliar$T(5)$ para determinar a temperatura média diária no 5º dia do ano. Então, poderíamos avaliar a função de custo nessa temperatura. Nós escreveríamos$C(T(5))$.

Figura$\PageIndex{1}$: Explicação de$C(T(5))$, qual é o custo da temperatura e$T(5)$ é a temperatura no dia 5.

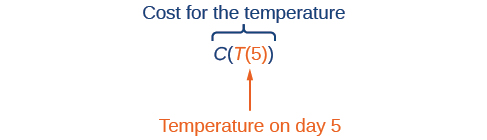
Ao combinar esses dois relacionamentos em uma função, realizamos a composição da função, que é o foco desta seção.

Combinando funções usando operações algébricas

A composição de funções é apenas uma forma de combinar funções existentes. Outra forma é realizar as operações algébricas usuais em funções, como adição, subtração, multiplicação e divisão. Fazemos isso executando as operações com as saídas da função, definindo o resultado como a saída da nossa nova função.

Suponha que precisemos adicionar duas colunas de números que representem a renda anual separada de marido e mulher durante um período de anos, com o resultado sendo a renda familiar total. Queremos fazer isso todos os anos, adicionando apenas a renda desse ano e coletando todos os dados em uma nova coluna. Se$w(y)$ é a renda da esposa e$h(y)$ é a renda anual do marido$y$, e queremos representar$T$ a renda total, então podemos definir uma nova função.

$$T(y)=h(y)+w(y) \nonumber$$

Se isso for válido para todos os anos, podemos nos concentrar na relação entre as funções sem referência a um ano e escrever

$$T=h+w \nonumber$$

Assim como para essa soma de duas funções, podemos definir funções de diferença, produto e razão para qualquer par de funções que tenha os mesmos tipos de entradas (não necessariamente números) e também os mesmos tipos de saídas (que precisam ser números para que as operações usuais de álgebra possam ser aplicadas a elas, e quais também deve ter as mesmas unidades ou nenhuma unidade quando adicionamos e subtraímos). Dessa forma, podemos pensar em somar, subtrair, multiplicar e dividir funções.

Para duas funções$f(x)$ e$g(x)$ com saídas de números reais, definimos novas funções$f+g$$f−g$,$fg$,, e$\frac{f}{g}$ pelas relações.

$$\begin{align*} (f+g)(x) &=f(x)+g(x) \\[4pt] (f−g)(x) &=f(x)−g(x) \\[4pt] (fg)(x)&=f(x)g(x) \\[4pt] \left(\dfrac{f}{g}\right)(x) &=\dfrac{f(x)}{g(x)} \end{align*}$$

Exemplo$\PageIndex{1}$: Performing Algebraic Operations on Functions

Encontre e simplifique as funções$(g−f)(x)$ e$\left(\dfrac{g}{f}\right)(x)$, dado$f(x)=x−1$$g(x)=x^2−1$ e. Eles têm a mesma função?

Solução

Comece escrevendo a forma geral e, em seguida, substitua as funções dadas.

$$\begin{align*} (g−f)(x) &= g(x)−f(x) \\[4pt] (g−f)(x) &=x^2−1−(x−1) \\[4pt] &=x^2−x \\[4pt] &=x(x−1) \end{align*}$$

$$\begin{align*} \left(\dfrac{g}{f}\right)(x)&=g(x)f(x) \\[4pt] \left(\dfrac{g}{f}\right)(x)&=\dfrac{x^2−1}{x−1} \\[4pt] &=\dfrac{(x+1)(x−1)}{x−1} \\[4pt]&=x+1 \end{align*}$$

Não, as funções não são as mesmas.

Nota: Para$\left(\dfrac{g}{f}\right)(x)$, a condição$x\neq1$ é necessária porque quando$x=1$, o denominador é igual a 0, o que torna a função indefinida.

Exercício$\PageIndex{1}$

Encontre e simplifique as funções$(fg)(x)$$(f−g)(x)$ e.

$$f(x)=x−1 \nonumber$$

e

$$g(x)=x^2−1 \nonumber$$

Eles têm a mesma função?

Resposta

$(fg)(x)=f(x)g(x)=(x−1)(x2−1)=x^3−x^2−x+1 \\[4pt] (f−g)(x)=f(x)−g(x)=(x−1)−(x^2−1)=x−x^2$

Não, as funções não são as mesmas.

Criar uma função pela composição de funções

A execução de operações algébricas em funções as combina em uma nova função, mas também podemos criar funções compondo funções. Quando queríamos calcular um custo de aquecimento a partir de um dia do ano, criamos uma nova função que usa um dia como entrada e gera um custo como saída. O processo de combinação de funções para que a saída de uma função se torne a entrada de outra é conhecido como composição de funções. A função resultante é conhecida como função composta. Representamos essa combinação com a seguinte notação:

$$f{\circ}g(x)=f(g(x))$$

Lemos o lado esquerdo como “$f$composto com$g$ em$x$” e o lado direito como “$f$$g$de”$x$. Os dois lados da equação têm o mesmo significado matemático e são iguais. O símbolo de círculo aberto$\circ$ é chamado de operador de composição. Usamos esse operador principalmente quando desejamos enfatizar a relação entre as próprias funções sem nos referir a nenhum valor de entrada específico. A composição é uma operação binária que assume duas funções e forma uma nova função, assim como a adição ou multiplicação usa dois números e fornece um novo número. No entanto, é importante não confundir composição de funções com multiplicação porque, como aprendemos acima, na maioria dos casos$f(g(x)){\neq}f(x)g(x)$.

Também é importante entender a ordem das operações na avaliação de uma função composta. Seguimos a convenção usual com parênteses, começando primeiro com os parênteses mais internos e depois trabalhando para o exterior. Na equação acima, a função$g$ pega a entrada$x$ primeiro e gera uma saída$g(x)$. Em seguida, a função$f$ recebe$g(x)$ como entrada e gera uma saída$f(g(x))$.

Figura$\PageIndex{2}$: Explicação da função composta.

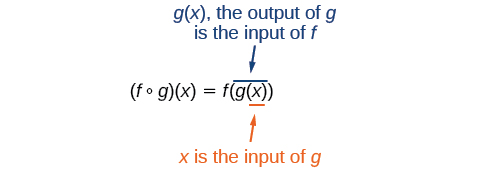
Em geral,$f{\circ}g$ e$g{\circ}f$ são funções diferentes. Em outras palavras, em muitos casos$f(g(x)){\neq}g(f(x))$ para todos$x$. Também veremos que às vezes duas funções podem ser compostas apenas em uma ordem específica.

Por exemplo, se$f(x)=x^2$ e$g(x)=x+2$, então

$$\begin{align*} f(g(x))&= f(x+2) \\[4pt]&=(x+2)^2 \\[4pt] &=x^2+4x+4 \end{align*}$$

mas

$$\begin{align*} g(f(x))&= g(x^2) \\[4pt]&=x^2+2 \end{align*}$$

Essas expressões não são iguais para todos os valores de x, então as duas funções não são iguais. É irrelevante que as expressões sejam iguais para o valor de entrada único$x=−\frac{1}{2}$.

Observe que o intervalo da função interna (a primeira função a ser avaliada) precisa estar dentro do domínio da função externa. Menos formalmente, a composição deve fazer sentido em termos de entradas e saídas.

Composição das funções

Quando a saída de uma função é usada como entrada de outra, chamamos toda a operação de uma composição de funções. Para qualquer entrada$x$ e função$f$ e$g$, essa ação define uma função composta, que escrevemos como$f{\circ}g$ tal que

$$(f{\circ}g)(x)=f(g(x))$$

O domínio da função composta$f{\circ}g$ é tudo$x$ o que$x$ está no domínio de$g$ e$g(x)$ está no domínio de$f$.

É importante perceber que o produto das funções não$fg$ é o mesmo que a composição da função$f(g(x))$, porque, em geral,$f(x)g(x){\neq}f(g(x))$.

Exemplo$\PageIndex{2}$: Determining whether Composition of Functions is Commutative

Usando as funções fornecidas, encontre$f(g(x))$$g(f(x))$ e. Determine se a composição das funções é comutativa.

$$f(x)=2x+1 \;\;\;\; g(x)=3−x \nonumber$$

Solução

Vamos começar$g(x)$ substituindo por$f(x)$.

$$\begin{align*} f(g(x))&= 2(3−x)+1 \\[4pt] &=6−2x+1 \\[4pt] &=7−2x \end{align*}$$

Agora podemos substituir$f(x)$ em$g(x)$.

$$\begin{align*} g(f(x))&= 3−(2x+1) \\[4pt]&=3−2x−1 \\[4pt] &=2-2x \end{align*}$$

Descobrimos que$g(f(x)){\neq}f(g(x))$, portanto, a operação da composição da função não é comutativa.

Exemplo$\PageIndex{3}$: Interpreting Composite Functions

A função$c(s)$ fornece o número de calorias queimadas ao completar os$s$ abdominais e$s(t)$ o número de abdominais que uma pessoa pode completar em$t$ minutos. Interpretar$c(s(3))$.

Solução

A expressão interna na composição é$s(3)$. Porque a entrada para a$s$ função -é tempo,$t=3$ representa 3 minutos e$s(3)$ é o número de flexões concluídas em 3 minutos.

Usar$s(3)$ como entrada para a função nos$c(s)$ dá o número de calorias queimadas durante o número de abdominais que podem ser concluídos em 3 minutos, ou simplesmente o número de calorias queimadas em 3 minutos (fazendo abdominais).

Exemplo$\PageIndex{4}$: Investigating the Order of Function Composition

Suponha que$f(x)$ forneça milhas que podem ser percorridas em$x$ horas e$g(y)$ forneça os galões de gasolina usados para dirigir$y$ milhas. Qual dessas expressões é significativa:$f(g(y))$ ou$g(f(x))$?

Solução

A função$y=f(x)$ é uma função cuja saída é o número de milhas percorridas correspondente ao número de horas percorridas.

$$\text{number of miles } =f (\text{number of hours}) \nonumber$$

A função$g(y)$ é uma função cuja saída é o número de galões usados correspondente ao número de milhas percorridas. Isso significa:

$$\text{number of gallons } =g(\text{number of miles}) \nonumber$$

A expressão$g(y)$ leva milhas como entrada e vários galões como saída. A função$f(x)$ requer um número de horas como entrada. Tentar inserir vários galões não faz sentido. A expressão$f(g(y))$ não tem sentido.

A expressão$f(x)$ leva horas como entrada e um número de milhas percorridas como saída. A função$g(y)$ requer um número de milhas como entrada. Usar$f(x)$ (milhas percorridas) como um valor de entrada para$g(y)$, onde galões de gás dependem das milhas percorridas, faz sentido. A expressão$g(f(x))$ faz sentido e produzirá o número de galões de gás usados$g$, dirigindo um certo número de milhas,$f(x)$, em$x$ horas.

Pergunta/resposta

Há alguma situação$f(g(y))$ em$g(f(x))$ que ambas seriam expressões significativas ou úteis?

Sim. Para muitas funções matemáticas puras, ambas as composições fazem sentido, embora geralmente produzam novas funções diferentes. Em problemas do mundo real, funções cujas entradas e saídas têm as mesmas unidades também podem fornecer composições que são significativas em qualquer ordem

Exercício$\PageIndex{2}$

A força gravitacional em um planeta a uma$r$ distância do sol é dada pela função$G(r)$. A aceleração de um planeta submetido a qualquer força$F$ é dada pela função$a(F)$. Forme uma composição significativa dessas duas funções e explique o que isso significa.

Resposta

Uma força gravitacional ainda é uma força, então$a(G(r))$ faz sentido como a aceleração de um planeta à$r$ distância do Sol (devido à gravidade), mas não$G(a(F))$ faz sentido.

Avaliando funções compostas

Depois de compor uma nova função a partir de duas funções existentes, precisamos ser capazes de avaliá-la para qualquer entrada em seu domínio. Faremos isso com entradas numéricas específicas para funções expressas como tabelas, gráficos e fórmulas e com variáveis como entradas para funções expressas como fórmulas. Em cada caso, avaliamos a função interna usando a entrada inicial e, em seguida, usamos a saída da função interna como entrada para a função externa.

Avaliando funções compostas usando tabelas

Ao trabalhar com funções fornecidas como tabelas, lemos os valores de entrada e saída das entradas da tabela e sempre trabalhamos de dentro para fora. Primeiro, avaliamos a função interna e depois usamos a saída da função interna como entrada para a função externa.

Exemplo$\PageIndex{5}$: Using a Table to Evaluate a Composite Function

Usando a tabela$\PageIndex{1}$,$f(g(3))$ avalie$g(f(3))$ e.

Tabela$\PageIndex{1}$

$x$	$f(x)$	$g(x)$
\ (x\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">1	\ (f (x)\)” style="alinhamento vertical: médio; alinhamento de texto: centro;” class="lt-math-1296">6	\ (g (x)\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">3
\ (x\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">2	\ (f (x)\)” style="alinhamento vertical: médio; alinhamento de texto: centro;” class="lt-math-1296">8	\ (g (x)\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">5
\ (x\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">3	\ (f (x)\)” style="alinhamento vertical: médio; alinhamento de texto: centro;” class="lt-math-1296">3	\ (g (x)\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">2
\ (x\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">4	\ (f (x)\)” style="alinhamento vertical: médio; alinhamento de texto: centro;” class="lt-math-1296">1	\ (g (x)\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">7

Solução

Para avaliar$f(g(3))$, começamos de dentro com o valor de entrada 3. Em seguida, avaliamos a expressão interna$g(3)$ usando a tabela que define a função$g: g(3)=2$. Podemos então usar esse resultado como entrada para a função$f$, então$g(3)$ é substituído por 2 e obtemos$f(2)$. Então, usando a tabela que define a função$f$, descobrimos isso$f(2)=8$.

$$g(3)=2 \nonumber$$

$$f(g(3))=f(2)=8 \nonumber$$

Para avaliar$g(f(3))$, primeiro avaliamos a expressão interna$f(3)$ usando a primeira tabela:$f(3)=3$. Em seguida, usando a tabela para$g$, podemos avaliar

$$g(f(3))=g(3)=2 \nonumber$$

A tabela$\PageIndex{2}$ mostra as funções compostas$f{\circ}g$ e$g{\circ}f$ como tabelas.

Tabela$\PageIndex{2}$

$x$	$g(x)$	$f(g(x))$	$f(x)$	$g(f(x))$
\ (x\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">3	\ (g (x)\)” style="vertical-align:middle; text-align:center;” class="lt-math-1296">2	\ (f (g (x))\)” style="alinhamento vertical: meio; alinhamento de texto: centro;” class="lt-math-1296">8	\ (f (x)\)” style="alinhamento vertical: médio; alinhamento de texto: centro;” class="lt-math-1296">3	\ (g (f (x))\)” style="alinhamento vertical: meio; alinhamento de texto: centro;” class="lt-math-1296">2

Exercício$\PageIndex{3}$

Usando a tabela$\PageIndex{1}$,$f(g(1))$ avalie$g(f(4))$ e.

Resposta

$f(g(1))=f(3)=3$e$g(f(4))=g(1)=3$

Avaliando funções compostas usando gráficos

Quando recebemos funções individuais como gráficos, o procedimento para avaliar funções compostas é semelhante ao processo que usamos para avaliar tabelas. Lemos os valores de entrada e saída, mas desta vez, dos eixos x e y dos gráficos.

Como...

Dada uma função composta e gráficos de suas funções individuais, avalie-a usando as informações fornecidas pelos gráficos.

1. Localize a entrada fornecida para a função interna no eixo x de seu gráfico.
2. Leia a saída da função interna do eixo y de seu gráfico.
3. Localize a saída da função interna no eixo x do gráfico da função externa.
4. Leia a saída da função externa do eixo y de seu gráfico. Essa é a saída da função composta.

Exemplo$\PageIndex{6}$: Using a Graph to Evaluate a Composite Function

Usando a Figura$\PageIndex{3}$, avalie$f(g(1))$.

Figura$\PageIndex{3}$: Dois gráficos de uma parábola positiva e negativa.

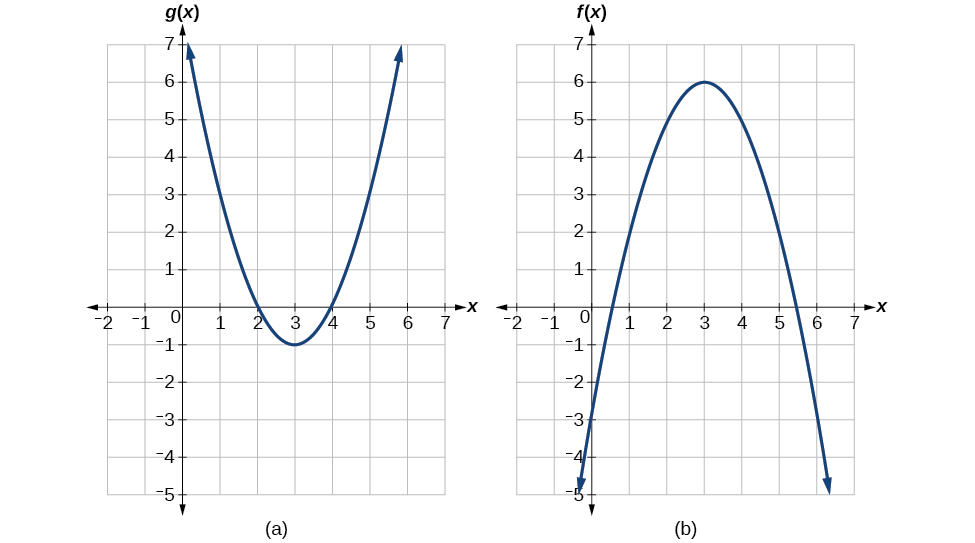
Solução

Para avaliar$f(g(1))$, começamos com a avaliação interna. Veja a Figura$\PageIndex{4}$.

Figura$\PageIndex{4}$: Dois gráficos de uma parábola positiva$g(x)$ e uma parábola negativa$f(x)$. Os seguintes pontos são plotados:$g(1)=3$$f(3)=6$ e.

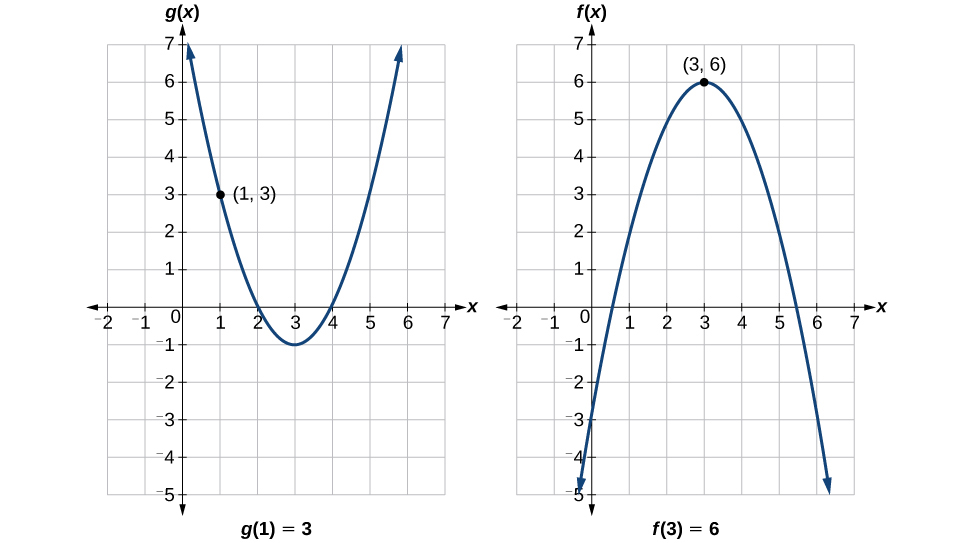
Avaliamos$g(1)$ usando o gráfico de$g(x)$, encontrando a entrada de 1 no eixo x e encontrando o valor de saída do gráfico nessa entrada. Aqui,$g(1)=3$. Usamos esse valor como entrada para a função$f$.

$$f(g(1))=f(3) \nonumber$$

Podemos então avaliar a função composta olhando para o gráfico de$f(x)$, encontrando a entrada de 3 no eixo x e lendo o valor de saída do gráfico nessa entrada. Aqui$f(3)=6$, então$f(g(1))=6$.

Análise

$\PageIndex{5}$A figura mostra como podemos marcar os gráficos com setas para traçar o caminho do valor de entrada até o valor de saída.

Figura$\PageIndex{5}$: Dois gráficos de uma parábola positiva e negativa.

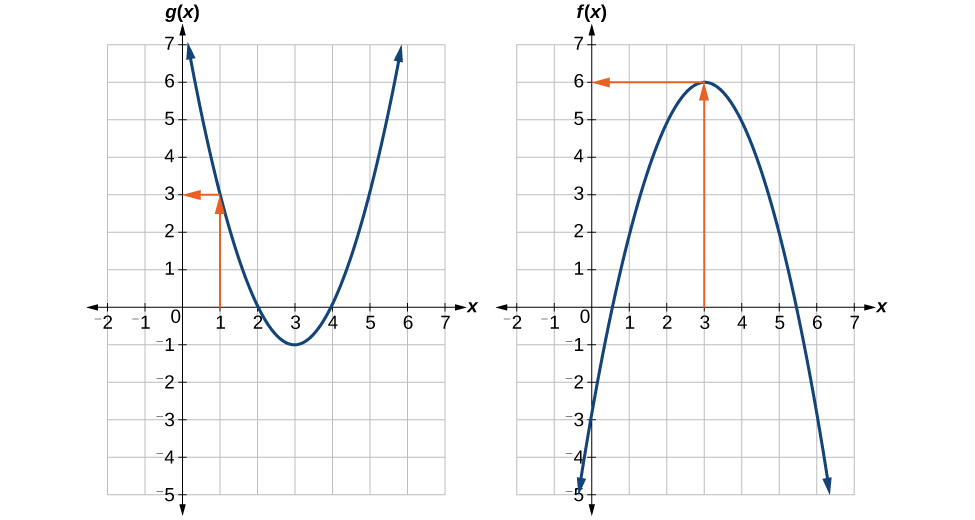
Exercício$\PageIndex{4}$

Usando a Figura$\PageIndex{3}$, avalie$g(f(2))$.

Resposta

$g(f(2))=g(5)=3$

Avaliando funções compostas usando fórmulas

Ao avaliar uma função composta em que criamos ou recebemos fórmulas, a regra de trabalhar de dentro para fora permanece a mesma. O valor de entrada para a função externa será a saída da função interna, que pode ser um valor numérico, um nome de variável ou uma expressão mais complicada.

Embora possamos compor as funções para cada valor de entrada individual, às vezes é útil encontrar uma única fórmula que calcule o resultado de uma composição$f(g(x))$. Para fazer isso, ampliaremos nossa ideia de avaliação de funções. Lembre-se de que, quando avaliamos uma função como$f(t)=t^2−t$, substituímos o valor dentro dos parênteses na fórmula sempre que vemos a variável de entrada.

Como...

Dada uma fórmula para uma função composta, avalie a função.

1. Avalie a função interna usando o valor de entrada ou a variável fornecida.
2. Use a saída resultante como entrada para a função externa.

Exemplo$\PageIndex{7}$: Evaluating a Composition of Functions Expressed as Formulas with a Numerical Input

Dado$f(t)=t^2−t$$h(x)=3x+2$ e avaliado$f(h(1))$.

Solução

Como a expressão interna é$h(1)$, começamos avaliando$h(x)$ em 1.

$$\begin{align*} h(1)=3(1)+2 \\[4pt] h(1)&=5 \end{align*}$$

Então$f(h(1))=f(5)$, então avaliamos$f(t)$ com uma entrada de 5.

$$\begin{align*} f(h(1)) &=f(5) \\[5pt] f(h(1))&=5^2−5 \\[5pt] f(h(1))&=20 \end{align*}$$

Análise

Não faz diferença quais$x$ foram chamadas$t$ as variáveis de entrada nesse problema porque avaliamos valores numéricos específicos.

Exercício$\PageIndex{5}$

Dado$f(t)=t^2−t$$h(x)=3x+2$ e avaliado

a.$h(f(2))$
b.$h(f(−2))$

Responda a um

8

Resposta b

20

Encontrando o domínio de uma função composta

Como discutimos anteriormente, o domínio de uma função composta, como$f{\circ}g$, depende do domínio$g$ e do domínio de$f$. É importante saber quando podemos aplicar uma função composta e quando não podemos, ou seja, conhecer o domínio de uma função como$f{\circ}g$. Vamos supor que conhecemos os domínios das funções$f$ e$g$ separadamente. Se escrevermos a função composta para uma entrada$x$ como$f(g(x))$, podemos ver imediatamente que$x$ deve ser um membro do domínio de g para que a expressão seja significativa, porque, caso contrário, não poderemos concluir a avaliação da função interna. No entanto, também vemos que$g(x)$ deve ser um membro do domínio de$f$, caso contrário, a segunda avaliação da função em$f(g(x))$ não pode ser concluída e a expressão ainda está indefinida. Assim, o domínio de$f{\circ}g$ consiste apenas nas entradas no domínio de$g$ que produzem saídas de$g$ pertencer ao domínio de$f$. Observe que o domínio de$f$ composto com$g$ é o conjunto de tudo$x$ isso que$x$ está no domínio de$g$ e g (x)\) está no domínio de$f$.

Definição: Domínio de uma função composta

O domínio de uma função composta$f(g(x))$ é o conjunto dessas entradas$x$ no domínio do$g$ para o qual$g(x)$ está no domínio de$f$.

Como...

Dada a composição da função$f(g(x))$, determine seu domínio.

1. Encontre o domínio de$g$.
2. Encontre o domínio de$f$.
3. Encontre essas entradas$x$ no domínio de$g$ para o qual$g(x)$ está no domínio de$f$. Ou seja, exclua essas entradas$x$ do domínio de$g$ para o qual não$g(x)$ está no domínio de$f$. O conjunto resultante é o domínio de$f{\circ}g$.

Exemplo$\PageIndex{8A}$: Finding the Domain of a Composite Function

Encontre o domínio de

$$(f∘g)(x) \text{ where } f(x)=\dfrac{5}{x−1} \text{ and } g(x)=\dfrac{4}{3x−2} \nonumber$$

Solução

O domínio de$g(x)$ consiste em todos os números reais$x=\frac{2}{3}$, exceto, pois esse valor de entrada nos faria dividir por 0. Da mesma forma, o domínio de$f$ consiste em todos os números reais, exceto 1. Portanto, precisamos excluir do domínio$g(x)$ esse valor de$x$ para o qual$g(x)=1$.

$$\begin{align*} \dfrac{4}{3x-2}&= 1 \\[4pt] 4 &=3x-2 \\[4pt] 6&=3x \\[4pt] x&= 2 \end{align*}$$

Portanto, o domínio de$f{\circ}g$ é o conjunto de todos os números reais, exceto$\frac{2}{3}$$2$ e. Isso significa que

$$x{\neq} \dfrac{2}{3} \text{ or } x\neq2 \nonumber$$

Podemos escrever isso em notação de intervalo como

$$\left(−\infty,\dfrac{2}{3}\right)\cup \left(\dfrac{2}{3},2 \right)\cup \left(2,\infty \right) \nonumber$$

Exemplo$\PageIndex{8B}$: Finding the Domain of a Composite Function Involving Radicals

Encontre o domínio de

$$(f{\circ}g)(x) \text{ where } f(x)=\sqrt{x+2} \text{ and } g(x)=\sqrt{3−x} \nonumber$$

Solução

Como não podemos obter a raiz quadrada de um número negativo, o domínio de$g$ é$\left(−\infty,3\right]$. Agora verificamos o domínio da função composta

$$(f{\circ}g)(x)=\sqrt{\sqrt{3−x}+2} \nonumber$$

$(f∘g)(x)=\sqrt{ \sqrt{3−x}+2},\sqrt{3−x}+2≥0,$Pois, o radicando de uma raiz quadrada deve ser positivo. Como as raízes quadradas são positivas$\sqrt{3−x}≥0$,, ou,$3−x≥0,$ o que dá um domínio de$(-∞,3]$.

Análise

Este exemplo mostra que o conhecimento da variedade de funções (especificamente a função interna) também pode ser útil para encontrar o domínio de uma função composta. Também mostra que o domínio de$f{\circ}g$ pode conter valores que não estão no domínio de$f$, embora devam estar no domínio de$g$.

Exercício$\PageIndex{6}$

Encontre o domínio de

$$(f{\circ}g)(x) \text{ where } f(x)=\dfrac{1}{x−2} \text{ and } g(x)=\sqrt{x+4} \nonumber$$

Resposta

$[−4,0)∪(0,∞)$

Decompondo uma função composta em suas funções componentes

Em alguns casos, é necessário decompor uma função complicada. Em outras palavras, podemos escrevê-lo como uma composição de duas funções mais simples. Pode haver mais de uma maneira de decompor uma função composta, então podemos escolher a decomposição que parece ser mais conveniente.

Exemplo$\PageIndex{9}$: Decomposing a Function

Escreva$f(x)=\sqrt{5−x^2}$ como a composição de duas funções.

Solução

Estamos procurando duas funções$g$ e$h$, portanto$f(x)=g(h(x))$. Para fazer isso, procuramos uma função dentro de uma função na fórmula para$f(x)$. Como uma possibilidade, podemos notar que a expressão$5−x^2$ está dentro da raiz quadrada. Poderíamos então decompor a função como

$$h(x)=5−x^2 \text{ and } g(x)=\sqrt{x} \nonumber$$

Podemos verificar nossa resposta recompondo as funções.

$$g(h(x))=g(5−x^2)=\sqrt{5−x^2} \nonumber$$

Exercício$\PageIndex{7}$

Escreva$f(x)=\dfrac{4}{3−\sqrt{4+x^2}}$ como a composição de duas funções.

Resposta

Respostas possíveis:

$g(x)=\sqrt{4+x^2}$

$h(x)=\dfrac{4}{3−x}$

$f=h{\circ}g$

Acesse esses recursos on-line para obter instruções e práticas adicionais com funções compostas.

• Funções compostas (http://openstaxcollege.org/l/compfunction)
• Aplicativo de notação de função composta (http://openstaxcollege.org/l/compfuncnot)
• Funções compostas usando gráficos (http://openstaxcollege.org/l/compfuncgraph)
• Funções de decomposição (http://openstaxcollege.org/l/decompfunction)
• Valores de funções compostas (http://openstaxcollege.org/l/compfuncvalue)

Equação chave

• Função composta$(f{\circ}g)(x)=f(g(x))$

Conceitos-chave

• Podemos realizar operações algébricas em funções. Veja o exemplo.
• Quando as funções são combinadas, a saída da primeira função (interna) se torna a entrada da segunda função (externa).
• A função produzida pela combinação de duas funções é uma função composta. Veja o exemplo e o exemplo.
• A ordem da composição da função deve ser considerada ao interpretar o significado das funções compostas. Veja o exemplo.
• Uma função composta pode ser avaliada avaliando a função interna usando o valor de entrada fornecido e, em seguida, avaliando a função externa tomando como entrada a saída da função interna.
• Uma função composta pode ser avaliada a partir de uma tabela. Veja o exemplo.
• Uma função composta pode ser avaliada a partir de um gráfico. Veja o exemplo.
• Uma função composta pode ser avaliada a partir de uma fórmula. Veja o exemplo.
• O domínio de uma função composta consiste nas entradas no domínio da função interna que correspondem às saídas da função interna que estão no domínio da função externa. Veja o exemplo e o exemplo.
• Assim como as funções podem ser combinadas para formar uma função composta, as funções compostas podem ser decompostas em funções mais simples.
• Muitas vezes, as funções podem ser decompostas de mais de uma forma. Veja o exemplo.

Glossário

função composta

a nova função formada pela composição da função, quando a saída de uma função é usada como entrada de outra