9.3: Fórmulas de ângulo duplo, meio ângulo e redução
- Page ID
- 186897
- Use fórmulas de ângulo duplo para encontrar valores exatos
- Use fórmulas de ângulo duplo para verificar identidades
- Use fórmulas de redução para simplificar uma expressão
- Use fórmulas de meio ângulo para encontrar valores exatos
As rampas de bicicleta feitas para competição (veja a Figura\(\PageIndex{1}\)) devem variar em altura, dependendo do nível de habilidade dos competidores. Para competidores avançados, o ângulo formado pela rampa e pelo solo deve ser\(\theta\) tal que\(\tan \theta=\dfrac{5}{3}\). O ângulo é dividido ao meio para iniciantes. Qual é a inclinação da rampa para iniciantes? Nesta seção, investigaremos três categorias adicionais de identidades que podemos usar para responder perguntas como essa.
Usando fórmulas de ângulo duplo para encontrar valores exatos
Na seção anterior, usamos fórmulas de adição e subtração para funções trigonométricas. Agora, vamos dar uma outra olhada nessas mesmas fórmulas. As fórmulas de ângulo duplo são um caso especial das fórmulas de soma, onde\(\alpha=\beta\). A derivação da fórmula de ângulo duplo para o seno começa com a fórmula da soma,
\[\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\]
Se deixarmos\(\alpha=\beta=\theta\), então temos
\[\begin{align*} \sin(\theta+\theta)&= \sin \theta \cos \theta+\cos \theta \sin \theta\\[4pt] \sin(2\theta)&= 2\sin \theta \cos \theta \end{align*}\]
Derivar o ângulo duplo para o cosseno nos dá três opções. Primeiro, começando pela fórmula da soma\(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\), e deixando\(\alpha=\beta=\theta\), temos
\[\begin{align*} \cos(\theta+\theta)&= \cos \theta \cos \theta-\sin \theta \sin \theta\\[4pt] \cos(2\theta)&= {\cos}^2 \theta - {\sin}^2 \theta \end{align*}\]
Usando as propriedades pitagóricas, podemos expandir essa fórmula de ângulo duplo para o cosseno e obter mais duas variações. A primeira variação é:
\[\begin{align*} \cos(2\theta)&= {\cos}^2 \theta - {\sin}^2 \theta \\[4pt] &= (1-{\sin}^2 \theta)-{\sin}^2 \theta \end{align*}\]
A segunda variação é:
\[\begin{align*} \cos(2\theta)&= {\cos}^2 \theta-{\sin}^2 \theta\\[4pt] &= {\cos}^2 \theta-(1-{\cos}^2 \theta)\\[4pt] &= 2 {\cos}^2 \theta-1 \end{align*}\]
Da mesma forma, para derivar a fórmula de ângulo duplo para tangente, substituir\(\alpha=\beta=\theta\) na fórmula de soma fornece
\[\begin{align*} \tan(\alpha+\beta)&= \dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\\[4pt] \tan(\theta+\theta)&= \dfrac{\tan \theta+\tan \theta}{1-\tan \theta \tan \theta}\\[4pt] \tan(2\theta)&= \dfrac{2\tan \theta}{1-{\tan}^2 \theta} \end{align*}\]
As fórmulas de ângulo duplo estão resumidas da seguinte forma:
\[\begin{align} \sin(2\theta)&= 2 \sin \theta \cos \theta\\[4pt] \cos(2\theta)&= {\cos}^2 \theta-{\sin}^2 \theta =1-2 {\sin}^2 \theta = 2{\cos}^2 \theta-1\\[4pt] \tan(2\theta)&= \dfrac{2 \tan \theta}{1-{\tan}^2\theta} \end{align}\]
- Desenhe um triângulo para refletir as informações fornecidas.
- Determine a fórmula correta de ângulo duplo.
- Substitua valores na fórmula com base no triângulo.
- Simplifique.
Dado que\(\tan \theta=−\dfrac{3}{4}\) e\(\theta\) está no quadrante II, encontre o seguinte:
- \(\sin(2\theta)\)
- \(\cos(2\theta)\)
- \(\tan(2\theta)\)
Solução
Se desenharmos um triângulo para refletir as informações fornecidas, poderemos encontrar os valores necessários para resolver os problemas na imagem. Recebemos\(\tan \theta=−\dfrac{3}{4}\), tal que\(\theta\) está no quadrante II. A tangente de um ângulo é igual ao lado oposto sobre o lado adjacente e, como\(\theta\) está no segundo quadrante, o lado adjacente está no eixo x e é negativo. Use o Teorema de Pitágoras para encontrar o comprimento da hipotenusa:
\[\begin{align*} {(-4)}^2+{(3)}^2&= c^2\\[4pt] 16+9&= c^2\\[4pt] 25&= c^2\\[4pt] c&= 5 \end{align*}\]
Agora podemos desenhar um triângulo semelhante ao mostrado na Figura\(\PageIndex{2}\).
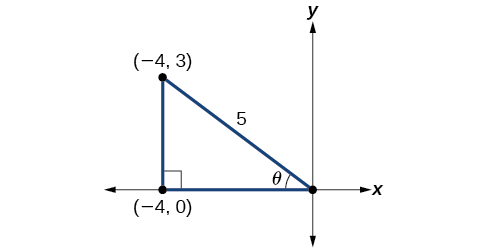
- Vamos começar escrevendo a fórmula de ângulo duplo para seno.
\(\sin(2\theta)=2 \sin \theta \cos \theta\)
Vemos que precisamos encontrar\(\sin \theta\)\(\cos \theta\) e. Com base na Figura\(\PageIndex{2}\), vemos que a hipotenusa é igual a\(5\)\(\sin θ=35\), então\(\sin θ=35\),\(\cos θ=−45\) e. Substitua esses valores na equação e simplifique.
Assim,
\[\begin{align*} \sin(2\theta)&= 2\left(\dfrac{3}{5}\right)\left(-\dfrac{4}{5}\right)\\[4pt] &= -\dfrac{24}{25} \end{align*}\]
- Escreva a fórmula de ângulo duplo para o cosseno.
\(\cos(2\theta)={\cos}^2 \theta−{\sin}^2 \theta\)
Novamente, substitua os valores do seno e do cosseno na equação e simplifique.
\[\begin{align*} \cos(2\theta)&= {\left(-\dfrac{4}{5}\right)}^2-{\left(\dfrac{3}{5}\right)}^2\\[4pt] &= \dfrac{16}{25}-\dfrac{9}{25}\\[4pt] &= \dfrac{7}{25} \end{align*}\]
- Escreva a fórmula de ângulo duplo para tangente.
\(\tan(2\theta)=\dfrac{2 \tan \theta}{1−{\tan}^2\theta}\)
Nesta fórmula, precisamos da tangente, que nos foi dada como\(\tan \theta=−\dfrac{3}{4}\). Substitua esse valor na equação e simplifique.
\ [\ begin {align*}\ tan (2\ theta) &=\ dfrac {2\ left (-\ dfrac {3} {4}\ right)} {1- {\ left (-\ dfrac {3} {4}\ direita)} ^2}\\ [4pt]
&=\ dfrac {-\ dfrac {3} {2}} {1-\ dfrac {9} {16}}\\ [4pt]
&= -\ dfrac {3} {2}\ left (\ dfrac {16} {7}\ direita)\\ [4pt]
&= -\ dfrac {24} {7}
\ end {align*}\]
Dado\(\sin \alpha=\dfrac{5}{8}\), com\(\theta\) no quadrante I, encontre\(\cos(2\alpha)\).
- Responda
-
\(\cos(2\alpha)=\dfrac{7}{32}\)
Use a fórmula de ângulo duplo para que o cosseno escreva\(\cos(6x)\) em termos de\(cos(3x)\).
Solução
\[\begin{align*} \cos(6x)&= \cos(3x+3x)\\[4pt] &= \cos 3x \cos 3x-\sin 3x \sin 3x\\[4pt] &= {\cos}^2 3x-{\sin}^2 3x \end{align*}\]
Análise
Este exemplo ilustra que podemos usar a fórmula de ângulo duplo sem ter valores exatos. Ele enfatiza que o padrão é o que precisamos lembrar e que as identidades são verdadeiras para todos os valores no domínio da função trigonométrica.
Usando fórmulas de ângulo duplo para verificar identidades
O estabelecimento de identidades usando as fórmulas de ângulo duplo é realizado usando as mesmas etapas que usamos para derivar as fórmulas de soma e diferença. Escolha o lado mais complicado da equação e reescreva-a até que ela coincida com o outro lado.
Verifique a seguinte identidade usando fórmulas de ângulo duplo:
\[1+\sin(2\theta)={(\sin\theta+\cos\theta)}^2 \nonumber \]
Solução
Trabalharemos no lado direito do sinal de igual e reescreveremos a expressão até que ela corresponda ao lado esquerdo.
\[\begin{align*} {(\sin \theta+\cos \theta)}^2&= {\sin}^2 \theta+2 \sin \theta \cos \theta+{\cos}^2 \theta\\[4pt] &= ({\sin}^2 \theta+{\cos}^2 \theta)+2 \sin \theta \cos \theta\\[4pt] &= 1+2 \sin \theta \cos \theta\\[4pt] &= 1+\sin(2\theta) \end{align*}\]
Análise
Esse processo não é complicado, desde que nos lembremos da fórmula quadrada perfeita da álgebra:
\[{(a\pm b)}^2=a^2\pm 2ab+b^2 \nonumber \]
onde\(a=\sin \theta\)\(b=\cos \theta\) e. Parte do sucesso em matemática é a capacidade de reconhecer padrões. Embora os termos ou símbolos possam mudar, a álgebra permanece consistente.
Verifique a identidade:\({\cos}^4 \theta−{\sin}^4 \theta=\cos(2\theta)\).
- Responda
-
\({\cos}^4 \theta−{\sin}^4 \theta=({\cos}^2 \theta+{\sin}^2 \theta)({\cos}^2 \theta−{\sin}^2 \theta)=\cos(2\theta)\)
Verifique a identidade:\(\tan(2 \theta)=2\cot \theta−\tan \theta\)
Solução
Nesse caso, trabalharemos com o lado esquerdo da equação e simplificaremos ou reescreveremos até que ela seja igual ao lado direito da equação.
\[\begin{align*} \tan(2\theta)&= \dfrac{2 \tan \theta}{1-{\tan}^2 \theta} \qquad \text{Double-angle formula}\\[4pt] &= \dfrac{2 \tan \theta\left (\dfrac{1}{\tan \theta}\right)}{(1-{\tan}^2 \theta)\left (\dfrac{1}{\tan \theta}\right )} \qquad \text{Multiply by a term that results in desired numerator}\\[4pt] &= \dfrac{2}{\dfrac{1}{\tan \theta}-\dfrac{ {\tan}^2 \theta}{\tan \theta}}\\[4pt] &= \dfrac{2}{\cot \theta-\tan \theta} \qquad \text {Use reciprocal identity for } \dfrac{1}{\tan \theta} \end{align*}\]
Análise
Aqui está um caso em que o lado mais complicado da equação inicial apareceu à direita, mas optamos por trabalhar no lado esquerdo. No entanto, se tivéssemos escolhido o lado esquerdo para reescrever, estaríamos trabalhando de trás para frente para chegar à equivalência. Por exemplo, suponha que quiséssemos mostrar
\[\begin{align*} \dfrac{2\tan \theta}{1-{\tan}^2 \theta}&= \dfrac{2}{\cot \theta-\tan \theta} \\[4pt] \text{Lets work on the right side}\\[4pt] \dfrac{2}{\cot \theta-\tan \theta}&= \frac{2}{\frac{1}{\tan \theta }-\tan \theta }\left ( \frac{\tan \theta }{\tan \theta } \right )\\[4pt] &= \dfrac{2 \tan \theta}{\dfrac{1}{\tan \theta}(\tan \theta)-\tan \theta(\tan \theta)}\\[4pt] &= \dfrac{2 \tan \theta}{1-{\tan}^2 \theta} \end{align*}\]
Ao usar as identidades para simplificar uma expressão trigonométrica ou resolver uma equação trigonométrica, geralmente há vários caminhos para o resultado desejado. Não existe uma regra definida sobre qual lado deve ser manipulado. No entanto, devemos começar com as diretrizes estabelecidas anteriormente.
Verifique a identidade:\(\cos(2\theta)\cos \theta={\cos}^3 \theta−\cos \theta {\sin}^2 \theta\).
- Responda
-
\(\cos(2 \theta)\cos \theta=({\cos}^2 \theta−{\sin}^2 \theta) \cos \theta={\cos}^3 \theta−\cos \theta {\sin}^2 \theta\)
Use fórmulas de redução para simplificar uma expressão
As fórmulas de ângulo duplo podem ser usadas para derivar as fórmulas de redução, que são fórmulas que podemos usar para reduzir a potência de uma determinada expressão envolvendo potências pares de seno ou cosseno. Eles nos permitem reescrever os poderes pares do seno ou cosseno em termos da primeira potência do cosseno. Essas fórmulas são especialmente importantes em cursos de matemática de nível superior, em particular cálculo. Também chamadas de fórmulas de redução de potência, três identidades estão incluídas e são facilmente derivadas das fórmulas de ângulo duplo.
Podemos usar duas das três fórmulas de ângulo duplo para cosseno para derivar as fórmulas de redução para seno e cosseno. Vamos começar com\(\cos(2\theta)=1−2 {\sin}^2 \theta\). Resolver para\({\sin}^2 \theta\):
\[\begin{align*} \cos(2\theta)&= 1-2 {\sin}^2 \theta\\[4pt] 2 {\sin}^2 \theta&= 1-\cos(2\theta)\\[4pt] {\sin}^2 \theta&= \dfrac{1-\cos(2\theta)}{2} \end{align*}\]
Em seguida, usamos a fórmula\(\cos(2\theta)=2 {\cos}^2 \theta−1\). Resolver para\({\cos}^2 \theta\):
\[\begin{align*} \cos(2\theta)&= 2 {\cos}^2 \theta-1\\[4pt] 1+\cos(2\theta)&= 2 {\cos}^2 \theta\\[4pt] \dfrac{1+\cos(2\theta)}{2}&= {\cos}^2 \theta \end{align*}\]
A última fórmula de redução é derivada escrevendo a tangente em termos de seno e cosseno:
\[\begin{align*} \tan^2 \theta &= \frac{\sin^2 \theta}{\cos^2 \theta} \\[4pt] &= \dfrac{\dfrac{1-\cos(2\theta)}{2}}{\dfrac{1+\cos(2\theta)}{2}} \qquad \tag{Substitute the reduction formulas} \\[4pt] &= \left(\dfrac{1-\cos(2 \theta)}{2}\right)\left(\dfrac{2}{1+\cos(2 \theta)}\right) \\[4pt] &= \dfrac{1-\cos(2 \theta)}{1+\cos(2 \theta)} \end{align*}\]
As fórmulas de redução estão resumidas da seguinte forma:
\[{\sin}^2 \theta=\dfrac{1−\cos(2 \theta)}{2}\]
\[{\cos}^2 \theta=\dfrac{1+\cos(2 \theta)}{2}\]
\[{\tan}^2 \theta=\dfrac{1−\cos(2 \theta)}{1+\cos(2 \theta)}\]
Escreva uma expressão equivalente para\({\cos}^4 x\) que não envolva nenhuma potência de seno ou cosseno maior que\(1\).
Solução
Aplicaremos a fórmula de redução do cosseno duas vezes.
\ [\ begin {align*}
{\ cos} ^4 x&= {({\ cos} ^2 x)} ^2\\ [4pt]
&= {\ left (\ dfrac {1+\ cos (2x)} {2}\ right)} ^2\ quad\ text {Fórmula de redução substituta}\\ [4pt]
&=\ dfrac {1} {4} (1+2\ cos (2x) + {\ cos} ^2 (2x))\\ [4pt]
&=\ dfrac {1} {4} +\ dfrac {1} {2}\ cos (2x) +\ dfrac {1} {4}\ left (\ dfrac {1+ {\ cos} ^2 (2x)} {2}\ right)\ quad\ text {Fórmula de redução substituta para} {\ cos} ^2 x\\ [4pt]
&=\ dfrac {1} {4} +\ dfrac {1} {2}\ cos (2x) +\ dfrac {1} {2}\ cos (2x) +\ dfrac c {1} {8} +\ dfrac {1} {8}\ cos (4x)\\ [4pt]
&=\ dfrac {3} {8} +\ dfrac {1} {2}\ cos (2x) +\ dfrac {1} {8}\ cos (4x)
\ fim {align*}\]
Análise
A solução é encontrada usando a fórmula de redução duas vezes, conforme observado, e a fórmula quadrada perfeita da álgebra.
Use as fórmulas de redução de potência para provar\({\sin}^3(2x)=\left[ \dfrac{1}{2} \sin(2x) \right] [ 1−\cos(4x) \)
Solução
Trabalharemos para simplificar o lado esquerdo da equação:
\[\begin{align*} {\sin}^3(2x)&= [\sin(2x)][{\sin}^2(2x)]\\[4pt] &= \sin(2x)\left [\dfrac{1-\cos(4x)}{2}\right ]\qquad \text{Substitute the power-reduction formula.}\\[4pt] &= \sin(2x)\left(\dfrac{1}{2}\right)[1-\cos(4x)]\\[4pt] &= \dfrac{1}{2}[\sin(2x)][1-\cos(4x)] \end{align*}\]
Análise
Observe que, neste exemplo, substituímos\(\dfrac{1−\cos(4x)}{2}\) por\({\sin}^2(2x)\). A fórmula afirma\({\sin}^2 \theta=\dfrac{1−\cos(2\theta)}{2}\)
Nós deixamos\(\theta=2x\), então\(2\theta=4x\).
Use as fórmulas de redução de potência para provar isso\(10{\cos}^4 x=\dfrac{15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x)\).
- Responda
-
\[\begin{align*} 10{\cos}^4 x&= 10{({\cos}^2x)}^2\\[4pt] &= 10{\left[\dfrac{ 1+\cos(2x)}{2} \right]}^2\qquad \text{Substitute reduction formula for } {\cos}^2x\\[4pt] &= \dfrac{10}{4}[1+2\cos(2x)+{\cos}^2(2x)]\\[4pt] &= \dfrac{10}{4}+\dfrac{10}{2}\cos(2x)+\dfrac{10}{4}\left(\dfrac{1+{\cos}^2(2x)}{2}\right)\qquad \text{ Substitute reduction formula for } {\cos}^2 x\\[4pt] &= \dfrac{10}{4}+\dfrac{10}{2} \cos(2x)+\dfrac{10}{8}+\dfrac{10}{8}\cos(4x)\\[4pt] &= \dfrac{30}{8}+5\cos(2x)+\dfrac{10}{8}\cos(4x)\\[4pt] &= \dfrac{15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x) \end{align*}\]
Usando fórmulas de meio ângulo para encontrar valores exatos
O próximo conjunto de identidades é o conjunto de fórmulas de meio ângulo, que pode ser derivado das fórmulas de redução e podemos usar quando temos um ângulo com metade do tamanho de um ângulo especial. Se\(\theta\) substituirmos por\(\dfrac{\alpha}{2}\), a fórmula do meio ângulo para o seno é encontrada simplificando a equação e resolvendo para\(\sin\left(\dfrac{\alpha}{2}\right)\). Observe que as fórmulas de meio ângulo são precedidas por um\(\pm\) sinal. Isso não significa que as expressões positivas e negativas sejam válidas. Pelo contrário, depende do quadrante em que\(\dfrac{\alpha}{2}\) termina.
A fórmula de meio ângulo para seno é derivada da seguinte forma:
\[\begin{align*} {\sin}^2 \theta&= \dfrac{1-\cos(2\theta)}{2}\\[4pt] {\sin}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\left(\cos 2\cdot \dfrac{\alpha}{2}\right)}{2}\\[4pt] &= \dfrac{1-\cos \alpha}{2}\\[4pt] \sin \left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1-\cos \alpha}{2}} \end{align*}\]
Para derivar a fórmula do meio ângulo para o cosseno, temos
\[\begin{align*} {\cos}^2 \theta&= \dfrac{1+\cos(2\theta)}{2}\\[4pt] {\cos}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1+\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{2}\\[4pt] &= \dfrac{1+\cos \alpha}{2}\\[4pt] \cos\left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1+\cos \alpha}{2}} \end{align*}\]
Para a identidade tangente, temos
\[\begin{align*} {\tan}^2 \theta&= \dfrac{1-\cos(2\theta)}{1+\cos(2\theta)}\\[4pt] {\tan}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{1+\cos\left(2\cdot \dfrac{\alpha}{2}\right)}\\[4pt] \tan\left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}} \end{align*}\]
As fórmulas de meio ângulo são as seguintes:
\[\begin{align} \sin\left(\dfrac{\alpha}{2}\right)&=\pm \sqrt{\dfrac{1-\cos \alpha}{2}} \label{halfsine} \\[4pt] \cos \left(\dfrac{\alpha}{2} \right) &=\pm \sqrt{\dfrac{1+\cos \alpha}{2}} \\[4pt] \tan\left(\dfrac{\alpha}{2}\right) &=\pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}} =\dfrac{\sin \alpha}{1+\cos \alpha} =\dfrac{1-\cos \alpha}{\sin \alpha}\end{align}\]
Usando uma fórmula de meio ângulo para encontrar o valor exato de uma função senoidal. Encontre\(\sin(15°)\) usando uma fórmula de meio ângulo.
Solução
Desde então\(15°=\dfrac{30°}{2}\), usamos a fórmula de meio ângulo para seno (Equation\ ref {halfsine}):
\ [\ begin {align*}
\ sin\ dfrac {30^ {\ circ}} {2} &=\ sqrt {\ dfrac {1-\ cos 30^ {\ circ}} {2}\ [4pt]
&=\ sqrt {\ dfrac {1-\ dfrac {\ sqrt {3}} {2}} {2}}\\\ [4pt]
&=\ sqrt {\ dfrac {\ dfrac {2-\ sqrt {3}} {2}} {2}}\\ [4pt]
&=\ sqrt {\ dfrac {2-\ sqrt {3}} {4}}\\ [4pt]
&=\ dfrac {\ sqrt {2-\ sqrt {3}}} {2}
\ end {align*}\]
Lembre-se de que podemos verificar a resposta com uma calculadora gráfica.
Análise
Observe que usamos apenas a raiz positiva porque\(\sin(15°)\) é positiva.
- Desenhe um triângulo para representar as informações fornecidas.
- Determine a fórmula correta do meio ângulo.
- Substitua valores na fórmula com base no triângulo.
- Simplifique.
Dado que\(\tan \alpha=\dfrac{8}{15}\)\(α\) está no quadrante III, encontre o valor exato do seguinte:
- \(\sin\left(\dfrac{\alpha}{2}\right)\)
- \(\cos\left(\dfrac{\alpha}{2}\right)\)
- \(\tan\left(\dfrac{\alpha}{2}\right)\)
Solução
Usando as informações fornecidas, podemos desenhar o triângulo mostrado na Figura\(\PageIndex{3}\). Usando o Teorema de Pitágoras, descobrimos que a hipotenusa é 17. Portanto, podemos calcular\(\sin \alpha=−\dfrac{8}{17}\)\(\cos \alpha=−\dfrac{15}{17}\) e.
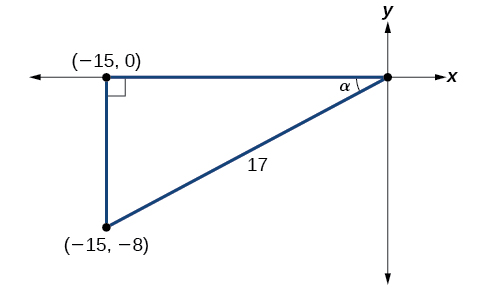
- Antes de começarmos, devemos lembrar que se\(α\) estiver no quadrante III, então\(180°<\alpha<270°\), sim\(\dfrac{180°}{2}<\dfrac{\alpha}{2}<\dfrac{270°}{2}\). Isso significa que o lado terminal de\(\dfrac{\alpha}{2}\) está no quadrante II, uma vez que\(90°<\dfrac{\alpha}{2}<135°\). Para descobrir\(\sin \dfrac{\alpha}{2}\), começamos escrevendo a fórmula de meio ângulo para seno. Em seguida, substituímos o valor do cosseno que encontramos no triângulo na Figura\(\PageIndex{3}\) e simplificamos. \[\begin{align*} \sin \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1-(-\dfrac{15}{17})}{2}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{32}{17}}{2}}\\[4pt] &= \pm \sqrt{\dfrac{32}{17}\cdot \dfrac{1}{2}}\\[4pt] &= \pm \sqrt{\dfrac{16}{17}}\\[4pt] &= \pm \dfrac{4}{\sqrt{17}}\\[4pt] &= \dfrac{4\sqrt{17}}{17} \end{align*}\]Escolhemos o valor positivo de\(\sin \dfrac{\alpha}{2}\) porque o ângulo termina no quadrante II e o seno é positivo no quadrante II.
- Para descobrir\(\cos \dfrac{\alpha}{2}\), escreveremos a fórmula do meio ângulo para o cosseno, substituiremos o valor do cosseno que encontramos do triângulo na Figura\(\PageIndex{3}\) e simplificaremos. \[\begin{align*} \cos \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1+\cos \alpha}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1+\left(-\dfrac{15}{17}\right)}{2}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{2}{17}}{2}}\\[4pt] &= \pm \sqrt{\dfrac{2}{17}\cdot \dfrac{1}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1}{17}}\\[4pt] &= -\dfrac{\sqrt{17}}{17} \end{align*}\]Escolhemos o valor negativo de\(\cos \dfrac{\alpha}{2}\) porque o ângulo está no quadrante II porque o cosseno é negativo no quadrante II.
- Para descobrir\(\tan \dfrac{\alpha}{2}\), escrevemos a fórmula de meio ângulo para tangente. Novamente, substituímos o valor do cosseno que encontramos no triângulo na Figura\(\PageIndex{3}\) e simplificamos. \[\begin{align*} \tan \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}}\\[4pt] &= \pm \sqrt{\dfrac{1-\left(-\dfrac{15}{17}\right)}{1+\left(-\dfrac{15}{17}\right)}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{32}{17}}{\dfrac{2}{17}}}\\[4pt] &= \pm \sqrt{\dfrac{32}{2}}\\[4pt] &= -\sqrt{16}\\[4pt] &= -4 \end{align*}\]Escolhemos o valor negativo de\(\tan \dfrac{\alpha}{2}\) porque\(\dfrac{\alpha}{2}\) está no quadrante II e a tangente é negativa no quadrante II.
Dado isso\(\sin \alpha=−\dfrac{4}{5}\) e se\(\alpha\) encontra no quadrante IV, encontre o valor exato de\(\cos \left(\dfrac{\alpha}{2}\right)\).
- Responda
-
\(-\dfrac{2}{\sqrt{5}}\)
Agora, retornaremos ao problema apresentado no início da seção. Uma rampa para bicicletas é construída para competições de alto nível com um ângulo\(θ\) formado pela rampa e pelo solo. Outra rampa deve ser construída com metade da inclinação para a competição de iniciantes. Se for\(tan θ=53\) para competição de alto nível, qual é a medida do ângulo da competição novata?
Solução
Como o ângulo da competição novata mede metade da inclinação do ângulo para a competição de alto nível e\(\tan \theta=\dfrac{5}{3}\) para a alta competição, podemos encontrar a\(\cos \theta\) partir do triângulo direito e do teorema de Pitágoras para que possamos usar as identidades de meio ângulo. Veja a Figura\(\PageIndex{4}\).
\[\begin{align*} 3^2+5^2&=34\\[4pt] c&=\sqrt{34} \end{align*}\]
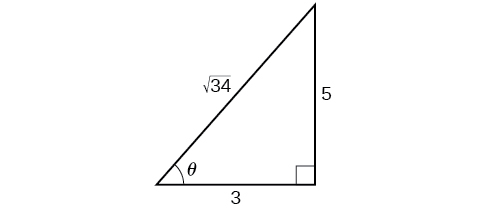
Nós vemos isso\(\cos \theta=\dfrac{3}{\sqrt{34}}=\dfrac{3\sqrt{34}}{34}\). Podemos usar a fórmula do meio ângulo para tangente:\(\tan \dfrac{\theta}{2}=\sqrt{\dfrac{1−\cos \theta}{1+\cos \theta}}\). Como\(\tan \theta\) está no primeiro quadrante, o mesmo acontece\(\tan \dfrac{\theta}{2}\).
\ [\ begin {align*}
\ tan\ dfrac {\ theta} {2} &=\ sqrt {\ dfrac {1-\ dfrac {3\ sqrt {34}} {34} {1+\ dfrac {3\ sqrt {34}} {34}}\\ [4pt]
&=\ sqrt {\ dfrac {\ dfrac {\ dfrac {\ dfrac {\ dfrac {\ dfrac {\ dfrac {\ dfrac {\ dfrac {\ dfrac {\ dfrac {\ dfrac {\ dfrac 34-3\ sqrt {34}} {34}} {\ dfrac {34+3\ sqrt {34}} {34}}\\ [4pt]
&=\ sqrt {\ dfrac {34-3\ sqrt {34}} {34+3\ sqrt {34}}}\\ [4pt]
&\ aprox. 0,57
\ end {align*}\]
Podemos pegar a tangente inversa para encontrar o ângulo:\({\tan}^{−1}(0.57)≈29.7°\). Portanto, o ângulo da rampa para a competição novata é\(≈29.7°\).
Acesse esses recursos on-line para obter instruções e práticas adicionais com fórmulas de ângulo duplo, meio ângulo e redução.
- Identidades de ângulo duplo
- Identidades de meio ângulo
Equações-chave
| Fórmulas de ângulo duplo |
\(\sin(2\theta)=2\sin \theta \cos \theta\) \(\cos(2\theta)={\cos}^2 \theta−{\sin}^2 \theta\) \(=1−2{\sin}^2 \theta\) \(=2{\cos}^2 \theta−1\) \(\tan(2\theta)=\dfrac{2\tan \theta}{1−{\tan}^2 \theta}\) |
| Fórmulas de redução |
\({\sin}^2 \theta=\dfrac{1−\cos(2\theta)}{2}\) \({\cos}^2 \theta=\dfrac{1+\cos(2\theta)}{2}\) \({\tan}^2 \theta=\dfrac{1−\cos(2\theta)}{1+\cos(2\theta)}\) |
| Fórmulas de meio ângulo |
\(\sin \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1−\cos \alpha}{2}}\) \(\cos \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1+\cos \alpha}{2}}\) \(\tan \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1−\cos \alpha}{1+\cos \alpha}}\) \(=\dfrac{\sin \alpha}{1+\cos \alpha}\) \(=\dfrac{1−\cos \alpha}{\sin \alpha}\) |
Conceitos-chave
- As identidades de ângulo duplo são derivadas das fórmulas de soma das funções trigonométricas fundamentais: seno, cosseno e tangente. Veja exemplo\(\PageIndex{1}\), exemplo\(\PageIndex{2}\)\(\PageIndex{3}\), exemplo e exemplo\(\PageIndex{4}\).
- As fórmulas de redução são especialmente úteis no cálculo, pois permitem reduzir o poder do termo trigonométrico. Veja o exemplo\(\PageIndex{5}\) e o exemplo\(\PageIndex{6}\).
- As fórmulas de meio ângulo nos permitem encontrar o valor das funções trigonométricas envolvendo meio-ângulos, independentemente de o ângulo original ser conhecido ou não. Veja exemplo\(\PageIndex{7}\)\(\PageIndex{8}\), exemplo e exemplo\(\PageIndex{9}\).


