9.2: Identidades de soma e diferença
- Page ID
- 186842
- Use fórmulas de soma e diferença para cosseno.
- Use fórmulas de soma e diferença para seno.
- Use fórmulas de soma e diferença para tangente.
- Use fórmulas de soma e diferença para cofunções.
- Use fórmulas de soma e diferença para verificar identidades.
Como a altura de uma montanha pode ser medida? E a distância da Terra ao sol? Como muitos problemas aparentemente impossíveis, contamos com fórmulas matemáticas para encontrar as respostas. As identidades trigonométricas, comumente usadas em provas matemáticas, têm sido aplicadas no mundo real há séculos, incluindo seu uso no cálculo de longas distâncias.
As identidades trigonométricas que examinaremos nesta seção podem ser atribuídas a um astrônomo persa que viveu por volta de 950 d.C., mas os antigos gregos descobriram essas mesmas fórmulas muito antes e as declararam em termos de acordes. São equações ou postulados especiais, verdadeiros para todos os valores inseridos nas equações e com inúmeras aplicações.

Nesta seção, aprenderemos técnicas que nos permitirão resolver problemas como os apresentados acima. As fórmulas a seguir simplificarão muitas expressões e equações trigonométricas. Lembre-se de que, ao longo desta seção, o termo fórmula é usado como sinônimo da palavra identidade.
Usando as fórmulas de soma e diferença para cosseno
Encontrar o valor exato do seno, cosseno ou tangente de um ângulo geralmente é mais fácil se pudermos reescrever o ângulo dado em termos de dois ângulos que têm valores trigonométricos conhecidos. Podemos usar os ângulos especiais, que podemos revisar no círculo unitário mostrado na Figura\(\PageIndex{2}\).
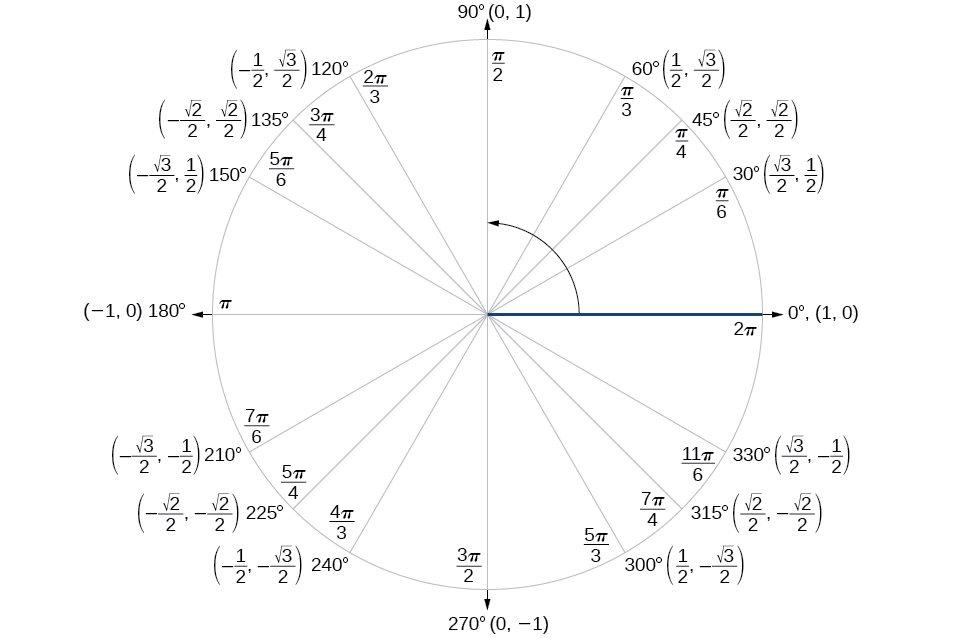
Começaremos com as fórmulas de soma e diferença para cosseno, para que possamos encontrar o cosseno de um determinado ângulo se pudermos dividi-lo na soma ou diferença de dois dos ângulos especiais (Tabela\(\PageIndex{1}\)).
| Fórmula de soma para cosseno | \(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\) |
| Fórmula de diferença para cosseno | \(\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\) |
Primeiro, provaremos a fórmula da diferença para cossenos. Vamos considerar dois pontos no círculo unitário (Figura\(\PageIndex{3}\)). \(P\)O ponto está em um ângulo\(\alpha\) do eixo positivo\(x\) com coordenadas\((\cos \alpha,\sin \alpha)\) e o ponto\(Q\) está em um ângulo\(\beta\) do eixo positivo\(x\) com coordenadas\((\cos \beta,\sin \beta)\). Observe que a medida do ângulo\(POQ\) é\(\alpha−\beta\).
Identifique mais dois pontos:\(A\) em um ângulo em relação ao eixo positivo\(x\) com coordenadas\((\cos(\alpha−\beta),\sin(\alpha−\beta))\); e ponto\(B\) com coordenadas\((1,0)\).\((\alpha−\beta)\) O triângulo\(POQ\) é uma rotação do triângulo\(AOB\) e, portanto, a distância de\(P\) para\(Q\) é a mesma que\(A\) a distância de\(B\) a.
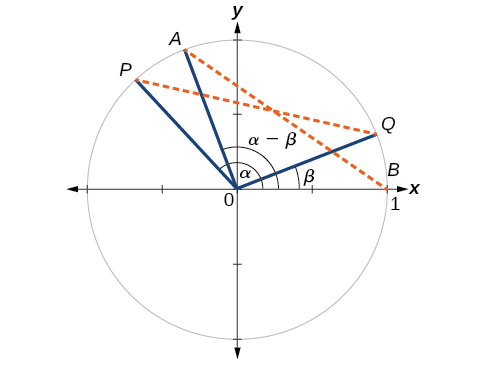
Podemos encontrar a distância de\(P\) até\(Q\) usando a fórmula da distância.
\ [\ begin {align*}
d_ {PQ} &=\ sqrt {{(\ cos\ alpha -\ cos\ beta)} ^2+ {(sin\ alpha - sin\ beta)} ^2}\\ [4pt]
&=\ sqrt {{\ cos} ^2\ alpha-2\ cos\ alpha\ cos\ beta+ {\ cos} ^2\ beta+\ sin} ^2\ alpha-2\ sin\ alpha\ sin\ beta+ {\ sin} ^2\ beta} & &\ text {Aplicar identidade pitagórica e simplificar.}\\ [4pt]
&=\ sqrt {({\ cos} ^2\ alpha+ {\ sin} ^2\ alpha) + ({\ cos} ^2\ beta+ {\ sin} ^2\ beta) -2\ cos\ alpha\ cos\ cos\ beta-2\ sin\ alpha\ sin\ beta}\\ [4pt]
&=\ sqrt {1+1-2\ cos\ alpha\ cos\ beta-2\ sin\ alpha\ sin\ beta}\\ [4pt]
&=\ sqrt {2-2\ cos\ alpha\ cos\ cos\ beta-2\ sin\ alpha\ sin\ beta}\ end {align*}\]
Da mesma forma, usando a fórmula da distância, podemos encontrar\(A\) a distância de\(B\) a.
\ [\ begin {align*}
d_ {AB} &=\ sqrt {{(\ cos (\ alpha-\ beta) -1)} ^2+ {(\ sin (\ alpha-\ beta) -0)} ^2}\\ [4pt]
&=\ sqrt {{\ cos} ^2 (\ alpha-\ beta) -2\ cos (\ alpha-\ beta) +1+ {sin} ^2 (\ alpha-\ beta)} & &\ text {Aplique a identidade pitagórica e simplifique}\\ [4pt]
&=\ sqrt {({\ cos} ^2 (\ alpha-\ beta) + {\ sin} ^2 (\ alpha-\ beta)) -2\ cos (\ alpha-\ beta) +1}\\ [4pt]
&=\ sqrt {1-2\ cos (\ alpha-\ beta) +1}\\ [4pt]
&=\ sqrt {2-2\ cos (\ alpha-\ beta)} & &\ text {Subtraia 2 de ambos os lados e divida ambos os lados por −2.}\\ [4pt]
\ cos\ alpha\ cos\ beta+\ sin\ alpha\ sin\ beta&=\ cos (\ alpha-\ beta)
\ end {align*}\]
Assim, temos a fórmula da diferença para o cosseno. Podemos usar métodos similares para derivar o cosseno da soma de dois ângulos.
Essas fórmulas podem ser usadas para calcular o cosseno de somas e diferenças de ângulos.
\[\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\]
\[\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\]
- Escreva a fórmula da diferença para o cosseno.
- Substitua os valores dos ângulos fornecidos na fórmula.
- Simplifique.
Usando a fórmula para o cosseno da diferença de dois ângulos, encontre o valor exato de\(\cos\left(\dfrac{5\pi}{4}−\dfrac{\pi}{6}\right)\).
Solução
Comece escrevendo a fórmula para o cosseno da diferença de dois ângulos. Em seguida, substitua os valores fornecidos.
\[\begin{align*} \cos(\alpha-\beta)&= \cos \alpha \cos \beta+\sin \alpha \sin \beta\\[4pt] \cos\left(\dfrac{5\pi}{4}-\dfrac{\pi}{6}\right)&= \cos\left(\dfrac{5\pi}{4}\right)\cos\left(\dfrac{\pi}{6}\right)+\sin\left(\dfrac{5\pi}{4}\right)\sin\left(\dfrac{\pi}{6}\right)\\[4pt] &= \left(-\dfrac{\sqrt{2}}{2}\right)\left(\dfrac{\sqrt{3}}{2}\right)-\left(\dfrac{\sqrt{2}}{2}\right )\left(\dfrac{1}{2}\right)\\[4pt] &= -\dfrac{\sqrt{6}}{4}-\dfrac{\sqrt{2}}{4}\\[4pt] &= \dfrac{-\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Lembre-se de que sempre podemos verificar a resposta usando uma calculadora gráfica no modo radiano.
Encontre o valor exato de\(\cos\left(\dfrac{\pi}{3}−\dfrac{\pi}{4}\right)\).
- Responda
-
\(\dfrac{\sqrt{2}+\sqrt{6}}{4}\)
Encontre o valor exato de\(\cos(75°)\).
Solução
Como\(75°=45°+30°\), podemos avaliar\(\cos(75°)\) como\(\cos(45°+30°)\).
\[\begin{align*} \cos(\alpha+\beta)&= \cos \alpha \cos \beta -\sin \alpha \sin \beta\\[4pt] \cos(45^{\circ}+30^{\circ})&= \cos(45^{\circ})\cos(30^{\circ})-\sin(45^{\circ})\sin(30^{\circ})\\[4pt] &= \dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}\right)-\dfrac{\sqrt{2}}{2}\left(\dfrac{1}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}}{4}-\dfrac{\sqrt{2}}{4}\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Lembre-se de que sempre podemos verificar a resposta usando uma calculadora gráfica no modo de graduação.
Análise
Observe que também poderíamos ter resolvido esse problema usando o fato de que\( 75°=135°−60°\).
\[\begin{align*} \cos(\alpha-\beta)&= \cos \alpha \cos \beta+\sin \alpha \sin \beta\\[4pt] \cos(135^{\circ}-60^{\circ})&= \cos(135^{\circ})\cos(60^{\circ})+\sin(135^{\circ})\sin(60^{\circ})\\[4pt] &= \left(-\dfrac{\sqrt{2}}{2}\right)\left(\dfrac{1}{2}\right)+\left(\dfrac{\sqrt{2}}{2}\right )\left(\dfrac{\sqrt{3}}{2}\right)\\[4pt] &= -\dfrac{\sqrt{2}}{4}+\dfrac{\sqrt{6}}{4}\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Encontre o valor exato de\(\cos(105°)\).
- Responda
-
\(\dfrac{\sqrt{2}-\sqrt{6}}{4}\)
Usando as fórmulas de soma e diferença para seno
As fórmulas de soma e diferença para o seno podem ser derivadas da mesma maneira que as do cosseno e se assemelham às fórmulas do cosseno.
Essas fórmulas podem ser usadas para calcular os senos de somas e diferenças de ângulos.
\[\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\]
\[\sin(\alpha−\beta)=\sin \alpha \cos \beta−\cos \alpha \sin \beta\]
- Escreva a fórmula da diferença para o seno.
- Substitua os ângulos fornecidos na fórmula.
- Simplifique.
Use as identidades de soma e diferença para avaliar a diferença dos ângulos e mostrar que a parte a é igual à parte b.
- \(\sin(45°−30°)\)
- \(\sin(135°−120°)\)
Solução
- Vamos começar escrevendo a fórmula e substituindo os ângulos fornecidos.
\[\begin{align*} \sin(\alpha-\beta)&= \sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] \sin(45^{\circ}-30^{\circ})&= \sin(45^{\circ})\cos(30^{\circ})-\cos(45^{\circ})\sin(30^{\circ}) \end{align*}\]
Em seguida, precisamos encontrar os valores das expressões trigonométricas.
\(\sin(45°)=\frac{\sqrt{2}}{2}, \qquad \cos(30°)=\frac{\sqrt{3}}{2}, \qquad \cos(45°)=\frac{\sqrt{2}}{2}, \qquad \sin(30°)=\frac{1}{2}\)
Agora podemos substituir esses valores na equação e simplificar.
\[\begin{align*} \sin(45°-30°)&= \dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}\right)-\dfrac{\sqrt{2}}{2}\left(\dfrac{1}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
- Novamente, escrevemos a fórmula e substituímos os ângulos fornecidos.
\[\begin{align*} \sin(\alpha-\beta)&= \sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] \sin(135^{\circ}-120^{\circ})&= \sin(135^{\circ})\cos(120^{\circ})-\cos(135^{\circ})\sin(120^{\circ}) \end{align*}\]
Em seguida, encontramos os valores das expressões trigonométricas.
\(\sin(135°)=\frac{\sqrt{2}}{2}, \qquad \cos(120°)=-\frac{1}{2}, \qquad \cos(135°)=\frac{\sqrt{2}}{2}, \qquad \sin(120°)=\frac{\sqrt{3}}{2}\)
Agora podemos substituir esses valores na equação e simplificar.
\[\begin{align*} \sin(135^{\circ}-120^{\circ})&= \dfrac{\sqrt{2}}{2}\left(-\dfrac{1}{2}\right)-\left(-\dfrac{\sqrt{2}}{2}\right)\left (\dfrac{\sqrt{3}}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Encontre o valor exato de\(\sin\left ({\cos}^{−1}\frac{1}{2}+{\sin}^{−1}\frac{3}{5}\right)\). Em seguida, verifique a resposta com uma calculadora gráfica.
Solução
O padrão exibido nesse problema é\(\sin(\alpha+\beta)\). Deixe\(\alpha={\cos}^{−1}\frac{1}{2}\)\(\beta={\sin}^{−1}\frac{3}{5}\) e. Então podemos escrever
\ [\ begin {align*}
\ cos\ alpha&=\ dfrac {1} {2},\ quad 0\ leq\ alpha\ leq\ pi\\ [4pt]
\ sin\ beta&=\ dfrac {3} {5},\ quad -\ dfrac {\ pi} {2}\ leq\ beta\ leq\ leq\ dfrac {\ pi} {2}\\[4pt]\end{align*}\]
Usaremos as identidades pitagóricas para encontrar\(\sin \alpha\) e\(\cos \beta\)
\ [\ begin {align*}
\ sin\ alpha&=\ sqrt {1- {\ cos} ^2\ alpha}\\ [4pt]
&=\ sqrt {1-\ dfrac {1} {4}\ [4pt]
&=\ sqrt {\ dfrac {3} {4}}\\ [4pt]
&=\ dfrac {\ sqrt {3}} {2}\\ [4pt]
\ cos\ beta&=\ sqrt {1- {\ sin} ^2\ beta}\\ [4pt]
& =\ sqrt {1-\ dfrac {9} {25}}\\ [4pt]
&=\ sqrt {\ dfrac {16} {25}}\\ [4pt]
&=\ dfrac {4} {5}
\ end {align*}\]
Usando a fórmula de soma para seno,
\[\begin{align*} \sin \left({\cos}^{-1}\tfrac{1}{2}+{\sin}^{-1}\tfrac{3}{5}\right)&= \sin(\alpha+\beta)\\[4pt] &= \sin \alpha \cos \beta+\cos \alpha \sin \beta\\[4pt] &= \dfrac{\sqrt{3}}{2}\cdot \dfrac{4}{5}+\dfrac{1}{2}\cdot \dfrac{3}{5}\\[4pt] &= \dfrac{4\sqrt{3}+3}{10} \end{align*}\]
Usando as fórmulas de soma e diferença para tangente
Encontrar valores exatos para a tangente da soma ou diferença de dois ângulos é um pouco mais complicado, mas, novamente, é uma questão de reconhecer o padrão.
Encontrar a soma da fórmula de dois ângulos para tangente envolve pegar o quociente das fórmulas de soma para seno e cosseno e simplificar. Lembre-se\(\tan x=\dfrac{\sin x}{\cos x}\), quando\(\cos x≠0\).
Vamos derivar a fórmula da soma da tangente.
\ [\ begin {align*}
\ tan\ left (\ alpha+\ beta\ right) &=\ dfrac {\ sin\ left (\ alpha+\ beta\ right)} {\ cos (\ alpha+\ beta)}\\ [6pt]
&=\ dfrac {\ sin\ alpha\ cos\ beta+\ cos\ alpha\ sin\ beta} {\\ alpha\ cos\ cos\ beta-\ sin\ alpha\ sin\ beta}\\ [6pt]
&=\ dfrac {\ dfrac {\ sin\ alpha \ cos\ beta+\ cos\ alpha\ sin\ beta} {\ cos\ alpha\ cos\ beta} {\ dfrac {\ cos\ alpha\ cos\ beta-\ sin\ alpha\ sin\ beta} {\ cos\ alpha\ cos\ beta}\\ [6pt]
&=\ dfrac {\ dfrac {\ sin\ alpha\ cos\ beta} {\\ alpha\ cos\ cos\ cos\ cos\ beta} +\ dfrac {\ cos\ alpha\ sin\ beta} {\ cos\ alpha\ cos\ beta} {\ dfrac {\ cos\ alpha\ cos\ cos\ cos\ cos\ beta} {\ cos\ alpha\ cos\ beta} -\ dfrac {\ sin\ alpha\ sin\ beta} {\ cos\ alpha\ cos\ beta}\\ [6pt]
&=\ dfrac {\ dfrac {\ sin\ alpha} {\ cos\ alpha} +\ dfrac {\ sin\ beta} {\ cos\ beta} {\ cos\ beta} {1-\ dfrac {\ sin\ sin\ alpha\ sin\ beta} {\ cos\ alpha\ cos\ beta}\\ [6pt]
&=\ dfrac {\ tan\ alpha+\ tan\ beta} {1-\ tan\ tan\ alfa\ tan\ beta}
\ end {align*}\]
Podemos derivar a fórmula da diferença para a tangente de forma semelhante.
As fórmulas de soma e diferença para tangente são:
\[\tan(\alpha+\beta)=\dfrac{\tan \alpha+\tan \beta}{1−\tan \alpha \tan \beta}\]
\[\tan(\alpha-\beta)=\dfrac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}\]
- Escreva a fórmula da soma para a tangente.
- Substitua os ângulos fornecidos na fórmula.
- Simplifique.
Encontre o valor exato de\(\tan\left(\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)\).
Solução
Vamos primeiro escrever a fórmula da soma da tangente e depois substituir os ângulos fornecidos na fórmula.
\ [\ begin {align*}
\ tan (\ alpha+\ beta) &=\ dfrac {\ tan\ alpha+\ tan\ beta} {1-\ tan\ alpha\ tan\ beta}\\ [4pt]
\ tan\ left (\ dfrac {\ pi} {6} +\ dfrac {\ pi} {4}\ direita) &=\ dfrac {\ tan esquerda (\ dfrac {\ pi} {6}\ direita) +\ tan\ left (\ dfrac {\ pi} {4}\ right)} {1-\ left (\ tan\ left (\ dfrac {\ pi} {6}\ direita)\ direita )\ left (\ tan\ left (\ dfrac {\ pi} {4}\ right)\ right)}\ end {align*}\]
Em seguida, determinamos os valores individuais da função dentro da fórmula:
\[\tan\left (\dfrac{\pi}{6}\right )= \dfrac{1}{\sqrt{3}}, \quad \text{and} \quad \tan\left (\dfrac{\pi}{4}\right) = 1\]
Então temos,
\ [\ begin {align*}\ tan\ left (\ dfrac {\ pi} {6} +\ dfrac {\ pi} {4}\ right) &=\ dfrac {\ dfrac {1} {\ sqrt {3}} +1} {1-\ left (\ dfrac {1} {\ sqrt {3}}\ right) (1)}\\ [6pt]
&=\ dfrac {\ dfrac {1+\ sqrt {3}} {\ sqrt {3}}} {\ dfrac {\ sqrt {3} -1} {\ sqrt {3}}\\ [6pt]
& amp; =\ dfrac {1+\ sqrt {3}} {\ sqrt {3}}\ cdot\ dfrac {\ sqrt {3}} {\ sqrt {3} -1}\\ [6pt]
&=\ dfrac {\ sqrt {3} +1} {\ sqrt {3} -1}
\ end {align*}\]
Encontre o valor exato de\(\tan\left (\dfrac{2\pi}{3}+\dfrac{\pi}{4}\right )\).
- Responda
-
\(\dfrac{1-\sqrt{3}}{1+\sqrt{3}}\)
Dado\(\sin \alpha=\frac{3}{5}, \quad 0<\alpha<\frac{\pi}{2},\) e\(\cos \beta=−\frac{5}{13}, \quad \pi<\beta<\frac{3\pi}{2}\),
achar
- \(\sin(\alpha+\beta)\)
- \(\cos(\alpha+\beta)\)
- \(\tan(\alpha+\beta)\)
- \(\tan(\alpha−\beta)\)
Solução
Podemos usar as fórmulas de soma e diferença para identificar a soma ou a diferença dos ângulos quando a razão de seno, cosseno ou tangente é fornecida para cada um dos ângulos individuais. Para fazer isso, construímos o que é chamado de triângulo de referência para ajudar a encontrar cada componente das fórmulas de soma e diferença.
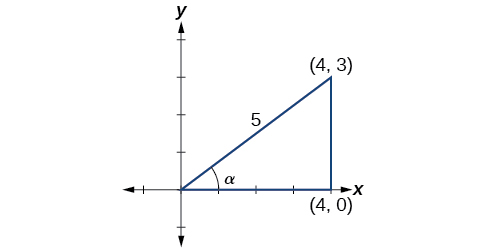
- Para encontrar\(\sin(\alpha+\beta)\), começamos com\(\sin \alpha=\dfrac{3}{5}\)\(0<\alpha<\dfrac{\pi}{2}\) e. O lado oposto\(\alpha\) tem comprimento 3, a hipotenusa tem comprimento 5 e\(\alpha\) está no primeiro quadrante. Veja a Figura\(\PageIndex{4}\). Usando o Teorema de Pitágoras, podemos encontrar o comprimento do lado\(a\):
\[\begin{align*} a^2+3^2&= 5^2\\[4pt] a^2&= 16\\[4pt] a&= 4 \end{align*}\]
Como\(\cos \beta=−\dfrac{5}{13}\) e\(\pi<\beta<\dfrac{3\pi}{2}\), o lado adjacente a\(\beta\)\(−5\) ele, a hipotenusa está\(13\) e\(\beta\) está no terceiro quadrante. Veja a Figura\(\PageIndex{5}\). Novamente, usando o Teorema de Pitágoras, temos
\[\begin{align*} {(-5)}^2+a^2&= {13}^2\\[4pt] 25+a^2&= 169\\[4pt] a^2&= 144\\[4pt] a&= \pm 12 \end{align*}\]
Já que\(\beta\) está no terceiro quadrante,\(a=–12\).
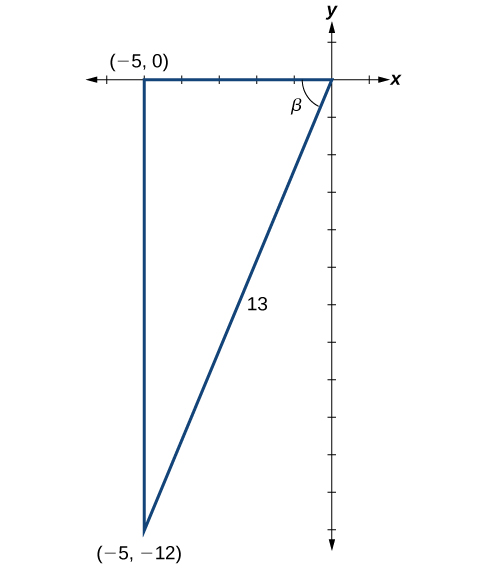
A próxima etapa é encontrar o cosseno de\(\alpha\) e o seno de\(\beta\). O cosseno de α α é o lado adjacente à hipotenusa. Podemos encontrá-lo no triângulo na Figura\(\PageIndex{5}\):\(\cos \alpha=\dfrac{4}{5}\). Também podemos encontrar o seno de\(\beta\) do triângulo na Figura\(\PageIndex{5}\), como lado oposto à hipotenusa:\(\sin \beta=−\dfrac{12}{13}\). Agora estamos prontos para avaliar\(\sin(\alpha+\beta)\).
\[\begin{align*} \sin(\alpha+\beta)&= \sin \alpha \cos \beta+\cos \alpha \sin \beta\\[4pt] &= \left(\dfrac{3}{5}\right)\left(-\dfrac{5}{13}\right )+\left (\dfrac{4}{5}\right )\left(-\dfrac{12}{13}\right )\\[4pt] &= -\dfrac{15}{65}-\dfrac{48}{65}\\[4pt] &= -\dfrac{63}{65} \end{align*}\]
- Podemos encontrar\(\cos(\alpha+\beta)\) de uma maneira semelhante. Substituímos os valores de acordo com a fórmula.
\[\begin{align*} \cos(\alpha+\beta)&= \cos \alpha \cos \beta-\sin \alpha \sin \beta\\[4pt] &= \left(\dfrac{4}{5}\right)\left(-\dfrac{5}{13}\right)-\left(\dfrac{3}{5}\right )\left(-\dfrac{12}{13}\right)\\[4pt] &= -\dfrac{20}{65}+\dfrac{36}{65}\\[4pt] &= \dfrac{16}{65} \end{align*}\]
- Para\(\tan(\alpha+\beta)\), se\(\sin \alpha=\dfrac{3}{5}\) e\(\cos \alpha=\dfrac{4}{5}\), então
\(\tan \alpha=\dfrac{\dfrac{3}{5}}{\dfrac{4}{5}}=\dfrac{3}{4}\)
Se\(\sin \beta=−\dfrac{12}{13}\) e\(\cos \beta=−\dfrac{5}{13}\), então
\(\tan \beta=\dfrac{−\dfrac{12}{13}}{−\dfrac{5}{13}}=\dfrac{12}{5}\)
Em seguida,
\ [\ begin {align*}
\ tan (\ alpha+\ beta) &=\ dfrac {\ tan\ alpha+\ tan\ beta} {1-\ tan\ alfa\ tan\ beta}\\ [6pt]
&=\ dfrac {\ dfrac {3} {4} +\ dfrac {12} {5}} {1-\ dfrac {3} {4}}\ left (\ dfrac {12} {5}\ direita)}\\ [6pt]
&=\ dfrac {\ dfrac {63} {20}} {-\ dfrac {16} {20}\ [6pt]
& amp; = -\ dfrac {63} {16}
\ end {align*}\]
- Para descobrir\(\tan(\alpha−\beta)\), temos os valores de que precisamos. Podemos substituí-los e avaliar.
\ [\ begin {align*}
\ tan (\ alpha-\ beta) &=\ dfrac {\ tan\ alpha-\ tan\ beta} {1+\ tan\ alfa\ tan\ beta}\\ [6pt]
&=\ dfrac {\ dfrac {\ dfrac {3} {4} -\ dfrac {12} {5}} {1+\ dfrac {3} {4} left (\ dfrac {12} {5}\ right)}\\ [6pt]
&=\ dfrac {-\ dfrac {33} {20}} {\ dfrac {56} {20}}\\ [6pt]
& amp; = -\ dfrac {33} {56}
\ end {align*}\]
Análise
Um erro comum ao abordar problemas como este é que podemos ficar tentados a pensar assim\(\alpha\) e\(\beta\) somos ângulos no mesmo triângulo, o que, claro, não são. Observe também que
\(\tan(\alpha+\beta)=\sin(\alpha+\beta)\cos(\alpha+\beta)\)
Usando fórmulas de soma e diferença para cofunções
Agora que podemos encontrar as funções seno, cosseno e tangente para as somas e diferenças de ângulos, podemos usá-las para fazer o mesmo com suas cofunções. Você pode se lembrar da Trigonometria do Triângulo Reto que, se a soma de dois ângulos positivos for\(\frac{\pi}{2}\), esses dois ângulos são complementos, e a soma dos dois ângulos agudos em um triângulo reto é\(\frac{\pi}{2}\), então eles também são complementos. Na Figura\(\PageIndex{6}\), observe que se um dos ângulos agudos for rotulado como\(\theta\), o outro ângulo agudo deverá ser rotulado\(\frac{\pi}{2}−\theta\).
Observe também isso\(\sin \theta=\cos\left(\frac{\pi}{2}−\theta\right)\), o que é oposto à hipotenusa. Assim, quando dois ângulos são complementares, podemos dizer que o seno de\(\theta\) é igual à cofunção do complemento de\(\theta\). Da mesma forma, tangente e cotangente são cofunções, e secante e cossecante são cofunções.
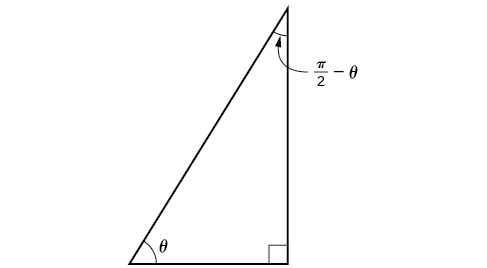
A partir dessas relações, as identidades de cofunção são formadas. Lembre-se de que você encontrou essas identidades pela primeira vez em The Unit Circle: Sine and Cosseno Functions.
As identidades da cofunção estão resumidas na Tabela\(\PageIndex{2}\).
| \(\sin \theta=\cos\left(\dfrac{\pi}{2}−\theta\right)\) | \(\cos \theta=\sin\left(\dfrac{\pi}{2}−\theta\right)\) |
| \(\tan \theta=\cot\left(\dfrac{\pi}{2}−\theta\right)\) | \(\cot \theta=\tan\left(\dfrac{\pi}{2}−\theta\right )\) |
| \(\sec \theta=\csc\left (\dfrac{\pi}{2}−\theta\right )\) | \(\csc \theta=\sec\left (\dfrac{\pi}{2}−\theta\right )\) |
Observe que as fórmulas na tabela também podem ser justificadas algebricamente usando as fórmulas de soma e diferença. Por exemplo, usando
\(\cos(\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\)
Nós podemos escrever
\[\begin{align*} \cos\left (\dfrac{\pi}{2}-\theta \right )&= \cos \dfrac{\pi}{2} \cos \theta+\sin \dfrac{\pi}{2} \sin \theta \\[4pt] &=(0)\cos \theta+(1)\sin \theta \\[4pt] &=\sin \theta \end{align*}\]
Escreva\(\tan \dfrac{\pi}{9}\) em termos de sua cofunção.
Solução
A cofunção de\(\tan \theta=\cot\left (\dfrac{\pi}{2}−\theta\right )\). Assim,
\[\begin{align*} \tan\left (\dfrac{\pi}{9}\right )&= \cot\left (\dfrac{\pi}{2}-\dfrac{\pi}{9}\right )\\[4pt] &= \cot\left (\dfrac{9\pi}{18}-\dfrac{2\pi}{18}\right )\\[4pt] &= \cot\left (\dfrac{7\pi}{18}\right ) \end{align*}\]
\(\sin \dfrac{\pi}{7}\) in terms of its Confunção de gravação.
- Responda
-
\(\cos\left (\dfrac{5\pi}{14}\right )\)
Usando as fórmulas de soma e diferença para verificar identidades
Verificar uma identidade significa demonstrar que a equação vale para todos os valores da variável. É útil estar muito familiarizado com as identidades ou ter uma lista delas acessível enquanto se trabalha com os problemas. A revisão das regras gerais apresentadas anteriormente pode ajudar a simplificar o processo de verificação de uma identidade.
- Comece com a expressão ao lado do sinal de igual que parece mais complexa. Reescreva essa expressão até que ela corresponda ao outro lado do sinal de igual. Ocasionalmente, podemos ter que alterar os dois lados, mas trabalhar em apenas um lado é o mais eficiente.
- Procure oportunidades de usar as fórmulas de soma e diferença.
- Reescreva somas ou diferenças de quocientes como quocientes únicos.
- Se o processo se tornar complicado, reescreva a expressão em termos de senos e cossenos.
Verifique a identidade\(\sin(\alpha+\beta)+\sin(\alpha−\beta)=2\sin \alpha \cos \beta\).
Solução
Vemos que o lado esquerdo da equação inclui os senos da soma e a diferença dos ângulos.
\(\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\)
\(\sin(\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta\)
Podemos reescrever cada uma usando as fórmulas de soma e diferença.
\[\begin{align*} \sin(\alpha+\beta)+\sin(\alpha-\beta)&= \sin \alpha \cos \beta+\cos \alpha \sin \beta+\sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] &= 2\sin \alpha \cos \beta \end{align*}\]
Vemos que a identidade foi verificada.
Verifique a identidade a seguir.
\(\dfrac{\sin(\alpha−\beta)}{\cos \alpha \cos \beta}=\tan \alpha−\tan \beta\)
Solução
Podemos começar reescrevendo o numerador no lado esquerdo da equação.
\[\begin{align*} \dfrac{\sin(\alpha-\beta)}{\cos \alpha \cos \beta}&= \dfrac{\sin \alpha \cos \beta-\cos \alpha \sin \beta}{\cos \alpha \cos \beta}\\[4pt] &= \dfrac{\sin \alpha \cos \beta}{\cos \alpha \cos \beta}-\dfrac{\cos \alpha \sin \beta}{\cos \alpha \cos \beta} & & \text{Rewrite using a common denominator}\\[4pt] &= \dfrac{\sin \alpha}{\cos \alpha}-\dfrac{\sin \beta}{\cos \beta} & & \text{Cancel}\\[4pt] &= \tan \alpha-\tan \beta & & \text{Rewrite in terms of tangent} \end{align*}\]
Verifique a identidade:\(\tan(\pi−\theta)=−\tan \theta\).
- Responda
-
\[\begin{align*} \tan(\pi-\theta)&= \dfrac{\tan(\pi)-\tan \theta}{1+\tan(\pi)\tan \theta}\\[4pt] &= \dfrac{0-\tan \theta}{1+0\cdot \tan \theta}\\[4pt] &= -\tan \theta \end{align*}\]
Deixe\(L_1\) e\(L_2\) denote duas linhas de interseção não verticais e deixe\(θ\) denotar o ângulo agudo entre\(L_1\)\(L_2\) e. Veja a Figura\(\PageIndex{7}\). Mostre isso
\(\tan \theta=\dfrac{m_2-m_1}{1+m_1m_2}\)
onde\(m_1\) e\(m_2\) são as inclinações de\(L_1\) e\(L_2\) respectivamente. (Dica: Use o fato de que\(\tan \theta_1=m_1\)\(\tan \theta_2=m_2\) e.)
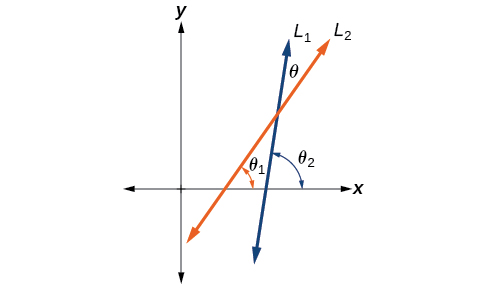
Solução
Usando a fórmula de diferença para tangente, esse problema não parece tão assustador quanto poderia.
\[\begin{align*} \tan \theta&= \tan(\theta_2-\theta_1)\\[4pt] &= \dfrac{\tan \theta_2-\tan \theta_1}{1+\tan \theta_1 \tan \theta_2}\\[4pt] &= \dfrac{m_2-m_1}{1+m_1m_2} \end{align*}\]
Para uma parede de escalada, um arame\(R\) é preso com\(47\) pés de altura em um poste vertical. O suporte adicional é fornecido por outro fio\(S\) preso,\(40\) pés acima do solo, no mesmo poste. Se os fios estiverem conectados aos\(50\) pés do solo a partir do poste, encontre o ângulo\(\alpha\) entre os fios. Veja a Figura\(\PageIndex{8}\).
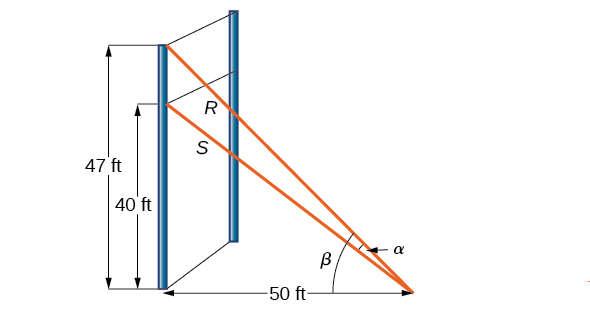
Solução
Primeiro, vamos resumir as informações que podemos coletar do diagrama. Como somente os lados adjacentes ao ângulo reto são conhecidos, podemos usar a função tangente. Observe isso\(\tan \beta=\frac{47}{50}\),\(\tan(\beta−\alpha)=\frac{40}{50}=\frac{4}{5}\) e. Podemos então usar a fórmula de diferença para tangente.
\[\tan(\beta-\alpha) = \dfrac{\tan \beta-\tan \alpha}{1+\tan \beta \tan \alpha}\]
Agora, substituindo os valores que conhecemos na fórmula, temos
\ [\ begin {align*}\ dfrac {4} {5} &=\ dfrac {\ tfrac {47} {50} -\ tan\ alpha} {1+\ tfrac {47} {50}\ tan\ alpha}\\ [4pt]
4\ left (1+\ tfrac {47} {47} 50}\ tan\ alpha\ direita) &= 5\ left (\ tfrac {47} {50} -\ tan\ alpha\ right)\ end {align*}\]
Use a propriedade distributiva e, em seguida, simplifique as funções.
\ [\ begin {align*} 4 (1) +4\ left (\ tfrac {47} {50}\ right)\ tan\ alpha &= 5\ left (\ tfrac {47} {50}\ direita) -5\ tan\ alpha\\ [4pt]
4+3,76\ tan\ alpha&= 4,7-5\ tan\ alpha\\ [4pt] 5\ tan\ alpha&= 4,7-5\ tan\ alpha\\ [4pt] 5\ tan\ alpha&= 4,7-5\ tan\ alpha\\ [4pt]
5\ tan\ alpha&= 4,7-5\ tan\ alpha\ +3,76\ tan\ alpha&= 0,7\\ [4 pontos]
8,76\ tan\ alpha&= 0,7\\ [4 pt]
\ tan\ alpha&\ approx 0,07991\\ [4pt]
\ tan^ {-1} (0,07991) &\ approx .079741\ end {align*}\]
Agora podemos calcular o ângulo em graus.
\ [\ begin {align*}\ alpha &\ approx 0,079741\ left (\ dfrac {180} {\ pi}\ right)\\ [4pt]
&\ approx 4,57^ {\ circ}
\ end {align*}\]
Análise
Ocasionalmente, quando aparece uma aplicação que inclui um triângulo reto, podemos pensar que resolver é uma questão de aplicar o Teorema de Pitágoras. Isso pode ser parcialmente verdade, mas depende do que o problema está perguntando e das informações fornecidas.
Acesse esses recursos on-line para obter instruções e práticas adicionais com identidades de soma e diferença.
- Identidades de soma e diferença para cosseno
- Identidades de soma e diferença para Sine
- Identidades de soma e diferença para tangente
Equações-chave
| Fórmula de soma para cosseno | \(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\) |
| Fórmula de diferença para cosseno | \(\cos(\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\) |
| Fórmula de soma para Sine | \(\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\) |
| Fórmula de diferença para Sine | \(\sin(\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta\) |
| Fórmula de soma para tangente | \(\tan(\alpha+\beta)=\dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\) |
| Fórmula de diferença para tangente | \(\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\) |
| Identidades de cofunção |
\(\sin \theta=\cos\left(\dfrac{\pi}{2}-\theta\right)\) \(\cos \theta=\sin\left(\dfrac{\pi}{2}-\theta\right)\) \(\tan \theta=\cot\left(\dfrac{\pi}{2}-\theta\right)\) \(\cot \theta=\tan\left(\dfrac{\pi}{2}-\theta\right)\) \(\sec \theta=\csc\left(\dfrac{\pi}{2}-\theta\right)\) \(\csc \theta=\sec\left(\dfrac{\pi}{2}-\theta\right)\) |
Conceitos-chave
- A fórmula da soma dos cossenos afirma que o cosseno da soma de dois ângulos é igual ao produto dos cossenos dos ângulos menos o produto dos senos dos ângulos. A fórmula da diferença para cossenos afirma que o cosseno da diferença de dois ângulos é igual ao produto dos cossenos dos ângulos mais o produto dos senos dos ângulos.
- As fórmulas de soma e diferença podem ser usadas para encontrar os valores exatos do seno, cosseno ou tangente de um ângulo. Veja o exemplo\(\PageIndex{1}\) e o exemplo\(\PageIndex{2}\).
- A fórmula da soma dos senos afirma que o seno da soma de dois ângulos é igual ao produto do seno do primeiro ângulo e cosseno do segundo ângulo mais o produto do cosseno do primeiro ângulo e do seno do segundo ângulo. A fórmula de diferença para senos afirma que o seno da diferença de dois ângulos é igual ao produto do seno do primeiro ângulo e cosseno do segundo ângulo menos o produto do cosseno do primeiro ângulo e do seno do segundo ângulo. Veja o exemplo\(\PageIndex{3}\).
- As fórmulas de soma e diferença para seno e cosseno também podem ser usadas para funções trigonométricas inversas. Veja o exemplo\(\PageIndex{4}\).
- A fórmula da soma da tangente afirma que a tangente da soma de dois ângulos é igual à soma das tangentes dos ângulos dividida por\(1\) menos o produto das tangentes dos ângulos. A fórmula de diferença para tangente afirma que a tangente da diferença de dois ângulos é igual à diferença das tangentes dos ângulos dividida por\(1\) mais o produto das tangentes dos ângulos. Veja o exemplo\(\PageIndex{5}\).
- O Teorema de Pitágoras, juntamente com as fórmulas de soma e diferença, podem ser usados para encontrar várias somas e diferenças de ângulos. Veja o exemplo\(\PageIndex{6}\).
- As identidades de cofunção se aplicam a ângulos complementares e pares de funções recíprocas. Veja o exemplo\(\PageIndex{7}\).
- As fórmulas de soma e diferença são úteis na verificação de identidades. Veja o exemplo\(\PageIndex{8}\) e o exemplo\(\PageIndex{9}\).
- Os problemas de aplicação geralmente são mais fáceis de resolver usando fórmulas de soma e diferença. Veja o exemplo\(\PageIndex{10}\) e o exemplo\(\PageIndex{11}\).


