9.1: Resolvendo equações trigonométricas com identidades
- Page ID
- 186870
- Verifique as identidades trigonométricas fundamentais.
- Simplifique as expressões trigonométricas usando a álgebra e as identidades.
Nos filmes de espionagem, vemos espiões internacionais com vários passaportes, cada um alegando uma identidade diferente. No entanto, sabemos que cada um desses passaportes representa a mesma pessoa. As identidades trigonométricas agem de forma semelhante a vários passaportes — há muitas maneiras de representar a mesma expressão trigonométrica. Assim como um espião escolhe um passaporte italiano ao viajar para a Itália, escolhemos a identidade que se aplica a um determinado cenário ao resolver uma equação trigonométrica.

Nesta seção, iniciaremos um exame das identidades trigonométricas fundamentais, incluindo como podemos verificá-las e como podemos usá-las para simplificar expressões trigonométricas.
Verificando as identidades trigonométricas fundamentais
As identidades nos permitem simplificar expressões complicadas. Eles são as ferramentas básicas da trigonometria usadas na resolução de equações trigonométricas, assim como fatorar, encontrar denominadores comuns e usar fórmulas especiais são as ferramentas básicas para resolver equações algébricas. Na verdade, usamos técnicas algébricas constantemente para simplificar as expressões trigonométricas. As propriedades básicas e as fórmulas da álgebra, como a fórmula da diferença dos quadrados e a fórmula dos quadrados perfeitos, simplificarão o trabalho envolvido com expressões e equações trigonométricas. Já sabemos que todas as funções trigonométricas estão relacionadas porque todas são definidas em termos do círculo unitário. Consequentemente, qualquer identidade trigonométrica pode ser escrita de várias maneiras.
Para verificar as identidades trigonométricas, geralmente começamos com o lado mais complicado da equação e essencialmente reescrevemos a expressão até que ela seja transformada na mesma expressão do outro lado da equação. Às vezes, precisamos fatorar expressões, expandir expressões, encontrar denominadores comuns ou usar outras estratégias algébricas para obter o resultado desejado. Nesta primeira seção, trabalharemos com as identidades fundamentais: as identidades pitagóricas, as identidades pares, as identidades recíprocas e as identidades quocientes.
Começaremos com as identidades pitagóricas (Tabela\(\PageIndex{1}\)), que são equações envolvendo funções trigonométricas baseadas nas propriedades de um triângulo reto. Já vimos e usamos a primeira dessas identificações, mas agora também usaremos identidades adicionais.
| \({\sin}^2 \theta+{\cos}^2 \theta=1\) | \(1+{\cot}^2 \theta={\csc}^2 \theta\) | \(1+{\tan}^2 \theta={\sec}^2 \theta\) |
A segunda e a terceira identidades podem ser obtidas manipulando a primeira. A identidade\(1+{\cot}^2 \theta={\csc}^2 \theta\) é encontrada reescrevendo o lado esquerdo da equação em termos de seno e cosseno.
Prove:\(1+{\cot}^2 \theta={\csc}^2 \theta\)
\[\begin{align*} 1+{\cot}^2 \theta&= (1+\dfrac{{\cos}^2}{{\sin}^2})\qquad \text{Rewrite the left side}\\ &= \left(\dfrac{{\sin}^2}{{\sin}^2}\right)+\left (\dfrac{{\cos}^2}{{\sin}^2}\right)\qquad \text{Write both terms with the common denominator}\\ &= \dfrac{{\sin}^2+{\cos}^2}{{\sin}^2}\\ &= \dfrac{1}{{\sin}^2}\\ &= {\csc}^2 \end{align*}\]
Da mesma forma,\(1+{\tan}^2 \theta={\sec}^2 \theta\) pode ser obtido reescrevendo o lado esquerdo dessa identidade em termos de seno e cosseno. Isso dá
\[\begin{align*} 1+{\tan}^2 \theta&= 1+{\left(\dfrac{\sin \theta}{\cos \theta}\right )}^2\qquad \text{Rewrite left side}\\ &= {\left (\dfrac{\cos \theta}{\cos \theta}\right )}^2+{\left (\dfrac{\sin \theta}{\cos \theta}\right)}^2\qquad \text{Write both terms with the common denominator}\\ &= \dfrac{{\cos}^2 \theta+{\sin}^2 \theta}{{\cos}^2 \theta}\\ &= \dfrac{1}{{\cos}^2 \theta}\\ &= {\sec}^2 \theta \end{align*}\]
Lembre-se de que determinamos quais funções trigonométricas são ímpares e quais são pares. O próximo conjunto de identidades fundamentais é o conjunto de identidades pares e ímpares. As identidades pares e ímpares relacionam o valor de uma função trigonométrica em um determinado ângulo com o valor da função no ângulo oposto (Tabela\(\PageIndex{2}\)).
| \(\tan(−\theta)=−\tan \theta\) | \(\sin(−\theta)=−\sin \theta\) | \(\cos(−\theta)=\cos \theta\) |
| \(\cot(−\theta)=−\cot \theta\) | \(\csc(−\theta)=−\csc \theta\) | \(\sec(−\theta)=\sec \theta\) |
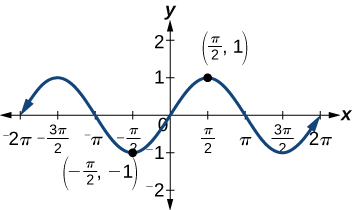
Lembre-se de que uma função ímpar é aquela em que,\(f(−x)= −f(x)\) para todos,\(x\) no domínio desligado. f. A função seno é uma função ímpar porque\(\sin(−\theta)=−\sin \theta\). O gráfico de uma função ímpar é simétrico em relação à origem. Por exemplo, considere as entradas correspondentes de\(\dfrac{\pi}{2}\)\(−\dfrac{\pi}{2}\) e. A saída de\(\sin\left (\dfrac{\pi}{2}\right )\) é oposta à saída de\(\sin \left (−\dfrac{\pi}{2}\right )\). Assim,
\[\begin{align*} \sin\left (\dfrac{\pi}{2}\right)&=1 \\[4pt] \sin\left (-\dfrac{\pi}{2}\right) &=-\sin\left (\dfrac{\pi}{2}\right) \\[4pt] &=-1 \end{align*}\]
Isso é mostrado na Figura\(\PageIndex{2}\).
Lembre-se de que uma função par é aquela em que
\(f(−x)=f(x)\)para todos\(x\) no domínio da\(f\)
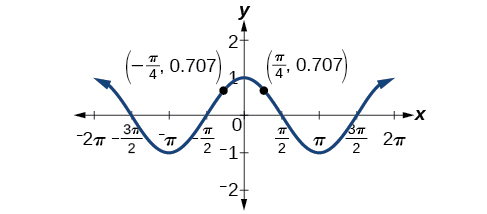
O gráfico de uma função par é simétrico em relação ao eixo y. A função cosseno é uma função uniforme porque\(\cos(−\theta)=\cos \theta\). Por exemplo, considere as entradas correspondentes\(\dfrac{\pi}{4}\)\(−\dfrac{\pi}{4}\) e. A saída de\(\cos\left (\dfrac{\pi}{4}\right)\) é a mesma que a saída de\(\cos\left (−\dfrac{\pi}{4}\right)\). Assim,
\[\begin{align*} \cos\left (−\dfrac{\pi}{4}\right ) &=\cos\left (\dfrac{\pi}{4}\right) \\[4pt] &≈0.707 \end{align*}\]
Veja a Figura\(\PageIndex{3}\).
Para todos\(\theta\) no domínio das funções seno e cosseno, respectivamente, podemos afirmar o seguinte:
- Desde então\(\sin(−\theta)=−\sin \theta\), seno é uma função estranha.
- Desde então\(\cos(−\theta)=\cos \theta\), o cosseno é uma função uniforme.
As outras identidades pares derivam da natureza par e ímpar das funções seno e cosseno. Por exemplo, considere a identidade tangente,\(\tan(−\theta)=−\tan \theta\). Podemos interpretar a tangente de um ângulo negativo como
\[\tan (−\theta)=\dfrac{\sin (−\theta)}{\cos (−\theta)}=\dfrac{−\sin \theta}{\cos \theta}=−\tan \theta. \nonumber\]
A tangente é, portanto, uma função ímpar, o que significa que\(\tan(−\theta)=−\tan(\theta)\) para todos\(\theta\) no domínio da função tangente.
A identidade cotangente,\(\cot(−\theta)=−\cot \theta\), também decorre das identidades seno e cosseno. Podemos interpretar a cotangente de um ângulo negativo como
\[\cot(−\theta)=\dfrac{\cos(−\theta)}{\sin(−\theta)}=\dfrac{\cos \theta}{−\sin \theta}=−\cot \theta.\nonumber\]
A cotangente é, portanto, uma função ímpar, o que significa que\(\cot(−\theta)=−\cot(\theta)\) para todos\(\theta\) no domínio da função cotangente.
A função cossecante é a recíproca da função senoidal, o que significa que a cossecante de um ângulo negativo será interpretada como
\[\csc(−\theta)=\dfrac{1}{\sin(−\theta)}=\dfrac{1}{−\sin \theta}=−\csc \theta. \nonumber\]
A função cossecante é, portanto, ímpar.
Finalmente, a função secante é a recíproca da função cosseno, e a secante de um ângulo negativo é interpretada como
\[\sec(−\theta)=\dfrac{1}{\cos(−\theta)}=\dfrac{1}{\cos \theta}=\sec \theta. \nonumber\]
A função secante é, portanto, uniforme.
Resumindo, apenas duas das funções trigonométricas, cosseno e secante, são pares. As outras quatro funções são ímpares, verificando as identidades pares e ímpares.
O próximo conjunto de identidades fundamentais é o conjunto de identidades recíprocas, que, como o nome indica, relacionam funções trigonométricas que são recíprocas entre si. (Tabela\(\PageIndex{3}\)). Lembre-se de que encontramos essas identidades pela primeira vez ao definir funções trigonométricas de ângulos retos na trigonometria de ângulo reto.
| \(\sin \theta=\dfrac{1}{\csc \theta}\) | \(\csc \theta=\dfrac{1}{\sin \theta}\) |
| \(\cos \theta = \dfrac{1}{\sec \theta}\) | \(\sec \theta=\dfrac{1}{\cos \theta}\) |
| \(\tan \theta=\dfrac{1}{\cot \theta}\) | \(\cot \theta=\dfrac{1}{\tan \theta}\) |
O conjunto final de identidades é o conjunto de identidades quocientes, que define relações entre certas funções trigonométricas e pode ser muito útil na verificação de outras identidades (Tabela\(\PageIndex{4}\)).
| \(\tan \theta=\dfrac{\sin \theta}{\cos \theta}\) | \(\cot \theta=\dfrac{\cos \theta}{\sin \theta}\) |
As identidades recíprocas e quocientes são derivadas das definições das funções trigonométricas básicas.
As identidades pitagóricas são baseadas nas propriedades de um triângulo reto.
\[{\cos}^2 \theta+{\sin}^2 \theta=1\]
\[1+{\cot}^2 \theta={\csc}^2 \theta\]
\[1+{\tan}^2 \theta={\sec}^2 \theta\]
As identidades pares e ímpares relacionam o valor de uma função trigonométrica em um determinado ângulo com o valor da função no ângulo oposto.
\[\tan(−\theta)=−\tan \theta\]
\[\cot(−\theta)=−\cot \theta\]
\[\sin(−\theta)=−\sin \theta\]
\[\csc(−\theta)=−\csc \theta\]
\[\cos(−\theta)=\cos \theta\]
\[\sec(−\theta)=\sec \theta\]
As identidades recíprocas definem os recíprocos das funções trigonométricas.
\[\sin \theta=\dfrac{1}{\csc \theta}\]
\[\cos \theta=\dfrac{1}{\sec \theta}\]
\[\tan \theta=\dfrac{1}{\cot \theta}\]
\[\csc \theta=\dfrac{1}{\sin \theta}\]
\[\sec \theta=\dfrac{1}{\cos \theta}\]
\[\cot \theta=\dfrac{1}{\tan \theta}\]
As identidades do quociente definem a relação entre as funções trigonométricas.
\[\tan \theta=\dfrac{\sin \theta}{\cos \theta}\]
\[\cot \theta=\dfrac{\cos \theta}{\sin \theta}\]
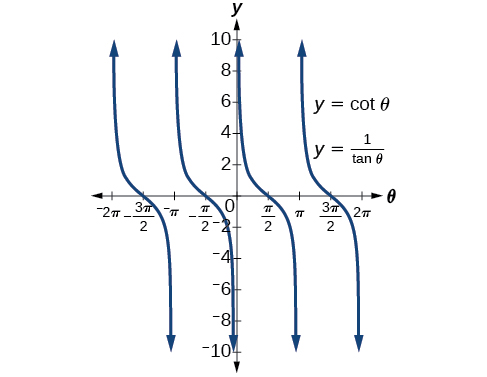
Faça um gráfico dos dois lados da identidade\(\cot \theta=\dfrac{1}{\tan \theta}\). Em outras palavras, na calculadora gráfica, gráfico\(y=\cot \theta\)\(y=\dfrac{1}{\tan \theta}\) e.
Solução
Veja a Figura\(\PageIndex{4}\).
Análise
Vemos apenas um gráfico porque ambas as expressões geram a mesma imagem. Um está em cima do outro. Essa é uma boa maneira de provar qualquer identidade. Se ambas as expressões fornecerem o mesmo gráfico, elas devem ser identidades.
- Trabalhe em um lado da equação. Geralmente, é melhor começar pelo lado mais complexo, pois é mais fácil simplificar do que construir.
- Procure oportunidades de fatorar expressões, quadrar um binômio ou adicionar frações.
- Observando quais funções estão na expressão final, procure oportunidades de usar as identidades e fazer as substituições adequadas.
- Se essas etapas não produzirem o resultado desejado, tente converter todos os termos em senos e cossenos.
Verificar\(\tan \theta \cos \theta=\sin \theta\).
Solução
Começaremos pelo lado esquerdo, pois é o lado mais complicado:
\[ \begin{align*} \tan \theta \cos \theta &=\left(\dfrac{\sin \theta}{\cos \theta}\right)\cos \theta \\[4pt] &=\sin \theta \end{align*}\]
Análise
Essa identidade era bastante simples de verificar, pois só exigia escrita\(\tan \theta\) em termos de\(\sin \theta\)\(\cos \theta\) e.
Verifique a identidade\(\csc \theta \cos \theta \tan \theta=1\).
- Responda
-
\[ \begin{align*} \csc \theta \cos \theta \tan \theta=\left(\dfrac{1}{\sin \theta}\right)\cos \theta\left(\dfrac{\sin \theta}{\cos \theta}\right) \\[4pt] & =\dfrac{\cos \theta}{\sin \theta}(\dfrac{\sin \theta}{\cos \theta}) \\[4pt] & =\dfrac{\sin \theta \cos \theta}{\sin \theta \cos \theta} \\[4pt] &=1 \end{align*}\]
Verifique a seguinte equivalência usando as identidades pares e ímpares:
\((1+\sin x)[1+\sin(−x)]={\cos}^2 x\)
Solução
Trabalhando no lado esquerdo da equação, temos
\( (1+\sin x)[1+\sin(−x)]=(1+\sin x)(1-\sin x)\)
Desde
\[\begin{align*} \sin(-x)&= -\sin x \\ [5pt] &=1-{\sin}^2 x\qquad \text{Difference of squares} \\ [5pt] &={\cos}^2 x \\ {\cos}^2 x&= 1-{\sin}^2 x \\ \end{align*}\]
Verifique a identidade\(\dfrac{{\sec}^2 \theta−1}{{\sec}^2 \theta}={\sin}^2 \theta\)
Solução
Como o lado esquerdo é mais complicado, vamos começar por aí.
\ [\ begin {align*}
\ dfrac {{\ sec} ^2\ theta-1} {{\ sec} ^2\ theta} &=\ dfrac {({\ tan} ^2\ theta +1) -1} {{\ sec} ^2\ theta}\\
{\ sec} ^2\ theta&= {\ tan} ^2\ theta +1\\
&=\ dfrac {{\ tan} ^2\ theta} {{\ sec} ^2\ theta}\\
&= {\ tan} ^2\ theta\ left (\ dfrac {1} {{\ sec} ^2\ theta}\ direita)\\
&= {\ tan} ^2\ theta\ esquerda ({\ cos} ^2\ theta\ direita)\\
{\ cos} ^2\ theta&=\ dfrac {1} {{\ sec} ^2\ theta}\\
&=\ left (\ dfrac {{\ sin} ^2\ theta} {{\ cos} ^2\ theta}\ right)\\
{\ tan} ^2\ theta&=\ dfrac {{\ sin} ^2\ theta} {{\ cos} ^2\ theta }\\
&= {\ sin} ^2\ theta
\ end {align*}\]
Há mais de uma maneira de verificar uma identidade. Aqui está outra possibilidade. Novamente, podemos começar pelo lado esquerdo.
\[\begin{align*} \dfrac{{\sec}^2 \theta-1}{{\sec}^2 \theta}&= \dfrac{{\sec}^2 \theta}{{\sec}^2 \theta}-\dfrac{1}{{\sec}^2 \theta}\\ &= 1-{\cos}^2 \theta\\ &= {\sin}^2 \theta \end{align*}\]
Análise
No primeiro método, usamos a identidade\({\sec}^2 \theta={\tan}^2 \theta+1\) e continuamos a simplificar. No segundo método, dividimos a fração, colocando os dois termos no numerador sobre o denominador comum. Esse problema ilustra que há várias maneiras de verificar uma identidade. Empregar um pouco de criatividade às vezes pode simplificar um procedimento. Desde que as substituições estejam corretas, a resposta será a mesma.
Mostre isso\(\dfrac{\cot \theta}{\csc \theta}=\cos \theta\).
- Responda
-
\[\begin{align*} \dfrac{\cot \theta}{\csc \theta}&= \dfrac{\tfrac{\cos \theta}{\sin \theta}}{\dfrac{1}{\sin \theta}}\\ &= \dfrac{\cos \theta}{\sin \theta}\cdot \dfrac{\sin \theta}{1}\\ &= \cos \theta \end{align*}\]
Crie uma identidade para a expressão\(2 \tan \theta \sec \theta\) reescrevendo estritamente em termos de seno.
Solução
Há várias maneiras de começar, mas aqui usaremos o quociente e as identidades recíprocas para reescrever a expressão:
\[\begin{align*} 2 \tan \theta \sec \theta&= 2\left (\dfrac{\sin \theta}{\cos \theta}\right )\left(\dfrac{1}{\cos \theta}\right )\\ &= \dfrac{2\sin \theta}{{\cos}^2 \theta}\\ &= \dfrac{2\sin \theta}{1-{\sin}^2 \theta}\qquad \text{Substitute } 1-{\sin}^2 \theta \text{ for } {\cos}^2 \theta \end{align*}\]
Assim,
\(2 \tan \theta \sec \theta=\dfrac{2 \sin \theta}{1−{\sin}^2 \theta}\)
Verifique a identidade:
\(\dfrac{{\sin}^2(−\theta)−{\cos}^2(−\theta)}{\sin(−\theta)−\cos(−\theta)}=\cos \theta−\sin \theta\)
Solução
Vamos começar pelo lado esquerdo e simplificar:
\[\begin{align*} \dfrac{{\sin}^2(-\theta)-{\cos}^2(-\theta)}{\sin(-\theta)-\cos(-\theta)}&= \dfrac{{[\sin(-\theta)]}^2-{[\cos(-\theta)]}^2}{\sin(-\theta)-\cos(-\theta)}\\ &= \dfrac{{(-\sin \theta)}^2-{(\cos \theta)}^2}{-\sin \theta -\cos \theta} \;\; \; , \sin(-x) = -\sin\space x\text { and } \cos(-x)=\cos \space x\\ &= \dfrac{{(\sin \theta)}^2-{(\cos \theta)}^2}{-\sin \theta -\cos \theta}\qquad \text{Difference of squares}\\ &= \dfrac{(\sin \theta-\cos \theta)(\sin \theta+\cos \theta)}{-(\sin \theta+\cos \theta)}\\ &= \cos \theta-\sin \theta \end{align*}\]
Verifique a identidade\(\dfrac{{\sin}^2 \theta−1}{\tan \theta \sin \theta−\tan \theta}=\dfrac{\sin \theta+1}{\tan \theta}\).
- Responda
-
\[\begin{align*} \dfrac{{\sin}^2 \theta-1}{\tan \theta \sin \theta-\tan \theta}&= \dfrac{(\sin \theta +1)(\sin \theta -1)}{\tan \theta(\sin \theta -1)}\\ &= \dfrac{\sin \theta+1}{\tan \theta} \end{align*}\]
Verifique a identidade:\((1−{\cos}^2 x)(1+{\cot}^2 x)=1\).
Solução
\[\begin{align*} (1-{\cos}^2 x)(1+{\cot}^2 x)&= (1-{\cos}^2 x)\left(1+\dfrac{{\cos}^2 x}{{\sin}^2 x}\right)\\ &= (1-{\cos}^2 x)\left(\dfrac{{\sin}^2 x}{{\sin}^2 x}+\dfrac{{\cos}^2 x}{{\sin}^2 x}\right )\qquad \text{Find the common denominator}\\ &= (1-{\cos}^2 x)\left(\dfrac{{\sin}^2 x +{\cos}^2 x}{{\sin}^2 x}\right)\\ &= ({\sin}^2 x)\left (\dfrac{1}{{\sin}^2 x}\right )\\ &= 1 \end{align*}\]
Usando álgebra para simplificar expressões trigonométricas
Vimos que a álgebra é muito importante na verificação de identidades trigonométricas, mas também é fundamental para simplificar expressões trigonométricas antes da resolução. Estar familiarizado com as propriedades e fórmulas básicas da álgebra, como a fórmula da diferença dos quadrados, a fórmula do quadrado perfeito ou a substituição, simplificará o trabalho envolvido com expressões e equações trigonométricas.
Por exemplo, a equação\((\sin x+1)(\sin x−1)=0\) se assemelha à equação\((x+1)(x−1)=0\), que usa a forma fatorada da diferença dos quadrados. Usar álgebra torna a busca de uma solução simples e familiar. Podemos definir cada fator igual a zero e resolver. Esse é um exemplo de reconhecimento de padrões algébricos em expressões ou equações trigonométricas.
Outro exemplo é a fórmula da diferença dos quadrados\(a^2−b^2=(a−b)(a+b)\), que é amplamente usada em muitas áreas além da matemática, como engenharia, arquitetura e física. Também podemos criar nossas próprias identidades expandindo continuamente uma expressão e fazendo as substituições apropriadas. O uso de propriedades e fórmulas algébricas torna muitas equações trigonométricas mais fáceis de entender e resolver.
Escreva a seguinte expressão trigonométrica como uma expressão algébrica:\(2{\cos}^2 \theta+\cos \theta−1\).
Solução
Observe que o padrão exibido tem a mesma forma de uma expressão quadrática padrão,\(ax^2+bx+c\). Deixando\(\cos \theta=x\), podemos reescrever a expressão da seguinte forma:
\(2x^2+x−1\)
Essa expressão pode ser considerada como\((2x+1)(x−1)\). Se fosse igual a zero e quiséssemos resolver a equação, usaríamos a propriedade do fator zero e resolveríamos cada fator para\(x\). Nesse ponto, substituiríamos por\(x\)\(\cos \theta\) e resolveríamos\(\theta\).
Reescreva a expressão trigonométrica usando a diferença de quadrados:\(4{cos}^2 \theta−1\).
Solução
Observe que tanto o coeficiente quanto a expressão trigonométrica no primeiro termo são quadrados, e o quadrado do número 1 é 1. Essa é a diferença dos quadrados.
\[\begin{align*} 4{\cos}^2 \theta-1&= {(2\cos \theta)}^2-1\\ &= (2\cos \theta-1)(2\cos \theta+1) \end{align*}\]
Análise
Se essa expressão fosse escrita na forma de um conjunto de equações igual a zero, poderíamos resolver cada fator usando a propriedade do fator zero. Também poderíamos usar a substituição como fizemos no problema anterior e deixar\(\cos \theta=x\), reescrever a expressão como\(4x^2−1\) e fatorar\((2x−1)(2x+1)\). Em seguida,\(x\) substitua por\(\cos \theta\) e resolva o ângulo.
Reescreva a expressão trigonométrica usando a diferença de quadrados:\(25−9{\sin}^2 \theta\).
- Responda
-
Esta é uma fórmula de diferença de quadrados:\(25−9{\sin}^2 \theta=(5−3\sin \theta)(5+3\sin \theta)\).
Simplifique a expressão reescrevendo e usando identidades:
\({\csc}^2 \theta−{\cot}^2 \theta\)
Solução
Podemos começar com a identidade pitagórica.
\[\begin{align*} 1+{\cot}^2 \theta&= {\csc}^2 \theta\\ \text{Now we can simplify by substituting } 1+{\cot}^2 \theta \text{ for } {\csc}^2 \theta\\ {\csc}^2 \theta-{\cot}^2 \theta&= 1+{\cot}^2 \theta-{\cot}^2 \theta\\ &= 1 \end{align*}\]
Use técnicas algébricas para verificar a identidade:\(\dfrac{\cos \theta}{1+\sin \theta}=\dfrac{1−\sin \theta}{\cos \theta}\).
(Dica: multiplique o numerador e o denominador no lado esquerdo por\(1−\sin \theta\).)
- Responda
-
\[\begin{align*} \dfrac{\cos \theta}{1+\sin \theta}\left(\dfrac{1-\sin \theta}{1-\sin \theta}\right)&= \dfrac{\cos \theta (1-\sin \theta)}{1-{\sin}^2 \theta}\\ &= \dfrac{\cos \theta (1-\sin \theta)}{{\cos}^2 \theta}\\ &= \dfrac{1-\sin \theta}{\cos \theta} \end{align*}\]
Acesse esses recursos on-line para obter instruções e práticas adicionais com as identidades trigonométricas fundamentais.
- Identidades trigonométricas fundamentais
- Verificando identidades trigonométricas
Equações-chave
| Identidades pitagóricas |
\({\cos}^2 \theta+{\sin}^2 \theta=1\) \(1+{\cot}^2 \theta={\csc}^2 \theta\) \(1+{\tan}^2 \theta={\sec}^2 \theta\) |
| Identidades pares ímpares |
\(\tan(−\theta)=-\tan \theta\) \(\cot(-\theta)=-\cot \theta\) \(\sin(-\theta)=-\sin \theta\) \(\csc(-\theta)=-\csc \theta\) \(\cos(-\theta)=\cos \theta\) \(\sec(-\theta)=\sec \theta\) |
| Identidades recíprocas |
\(\sin \theta=\dfrac{1}{\csc \theta}\) \(\cos \theta=\dfrac{1}{\sec \theta}\) \(\tan \theta=\dfrac{1}{\cot \theta}\) \(\csc \theta=\dfrac{1}{\sin \theta}\) \(\sec \theta=\dfrac{1}{\cos \theta}\) \(\cot \theta=\dfrac{1}{\tan \theta}\) |
| Identidades de quociente |
\(\tan \theta=\dfrac{\sin \theta}{\cos \theta}\) \(\cot \theta=\dfrac{\cos \theta}{\sin \theta}\) |
Conceitos-chave
- Há várias maneiras de representar uma expressão trigonométrica. A verificação das identidades ilustra como as expressões podem ser reescritas para simplificar um problema.
- Representar graficamente os dois lados de uma identidade a verificará. Veja o exemplo\(\PageIndex{1}\).
- Simplificar um lado da equação para igualar o outro lado é outro método para verificar uma identidade. Veja o exemplo\(\PageIndex{2}\) e o exemplo\(\PageIndex{3}\).
- A abordagem para verificar uma identidade depende da natureza da identidade. Muitas vezes, é útil começar pelo lado mais complexo da equação. Veja o exemplo\(\PageIndex{4}\).
- Podemos criar uma identidade e depois verificá-la. Veja o exemplo\(\PageIndex{5}\).
- Verificar uma identidade pode envolver álgebra com as identidades fundamentais. Veja o exemplo\(\PageIndex{6}\) e o exemplo\(\PageIndex{7}\).
- Técnicas algébricas podem ser usadas para simplificar expressões trigonométricas. Usamos técnicas algébricas em todo este texto, pois elas consistem nas regras fundamentais da matemática. Veja exemplo\(\PageIndex{8}\)\(\PageIndex{9}\), exemplo e exemplo\(\PageIndex{10}\).


