5.6: Funções racionais
- Page ID
- 187155
Objetivos de
- Use a notação de seta.
- Resolva problemas aplicados envolvendo funções racionais.
- Encontre os domínios das funções racionais.
- Identifique assíntotas verticais.
- Identifique assíntotas horizontais.
- Grafe funções racionais.
Suponha que saibamos que o custo de fabricação de um produto depende do número de itens,\(x\), produzidos. Isso é dado pela equação.\(C (x)=15,000x−0.1x^2+1000.\) Se quisermos saber o custo médio de produção de\(x\) itens, dividiríamos a função de custo pelo número de itens,\(x\). A função de custo médio, que gera o custo médio por item dos\(x\) itens produzidos, é
\[f(x)=\dfrac{15,000x−0.1x^2+1000}{x} \nonumber\]
Muitos outros problemas de aplicação exigem encontrar um valor médio de forma semelhante, fornecendo variáveis no denominador. Escrita sem uma variável no denominador, essa função conterá uma potência inteira negativa.
Nas últimas seções, trabalhamos com funções polinomiais, que são funções com números inteiros não negativos para expoentes. Nesta seção, exploramos funções racionais, que têm variáveis no denominador.
Usando a notação de seta
Vimos os gráficos da função recíproca básica e da função recíproca quadrada em nosso estudo das funções do kit de ferramentas. Examine esses gráficos, conforme mostrado na Figura\(\PageIndex{1}\), e observe algumas de suas características.
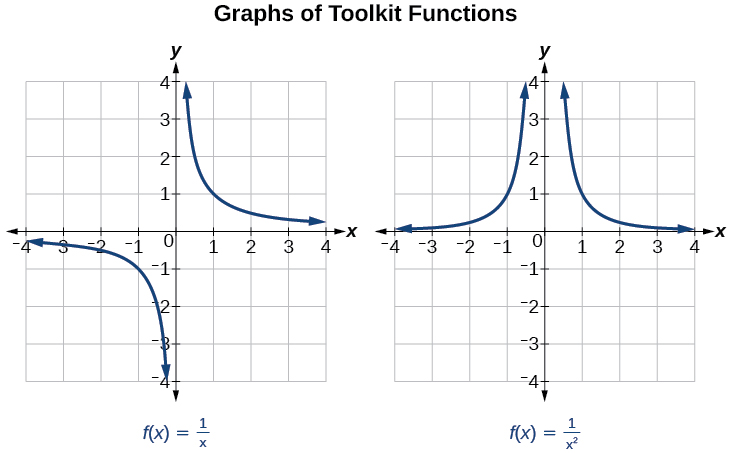
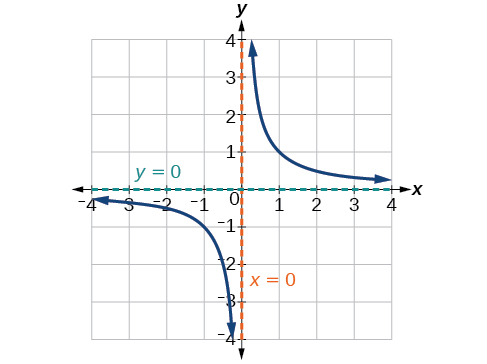
Várias coisas ficam aparentes se examinarmos o gráfico de\(f(x)=\frac{1}{x}\).
- No ramo esquerdo do gráfico, a curva se aproxima do\(x\) eixo\((y=0)\) -como\(x\rightarrow -\infty\).
- À medida que o gráfico se aproxima\(x = 0\) da esquerda, a curva cai, mas quando nos aproximamos de zero pela direita, a curva aumenta.
- Finalmente, na ramificação direita do gráfico, as curvas se aproximam do\(x\) eixo\((y=0) \) -como\(x\rightarrow \infty\).
Para resumir, usamos a notação de seta para mostrar que\(x\) ou\(f (x)\) está se aproximando de um determinado valor (Tabela\(\PageIndex{1}\)).
| Símbolo | Significado |
|---|---|
| \(x\rightarrow a^-\) | \(x\)se aproxima de a pela esquerda (\(x<a\)mas perto de\(a\)) |
| \(x\rightarrow a^+\) | \(x\)se aproxima de a pela direita (\(x>a\)mas perto de\(a\)) |
| \(x\rightarrow \infty\) | \(x\)se aproxima do infinito (\(x\)aumenta sem limite) |
| \(x\rightarrow −\infty\) | \(x\)se aproxima do infinito negativo (\(x\)diminui sem limite) |
| \(f(x)\rightarrow \infty\) | a saída se aproxima do infinito (a saída aumenta sem limite) |
| \(f(x)\rightarrow −\infty\) | a saída se aproxima do infinito negativo (a saída diminui sem limite) |
| \(f(x)\rightarrow a\) | as abordagens de saída\(a\) |
Comportamento local de\(f(x)=\frac{1}{x}\)
Vamos começar examinando a função recíproca,\(f(x)=\frac{1}{x}\). Não podemos dividir por zero, o que significa que a função é indefinida em\(x=0\); então zero não está no domínio. À medida que os valores de entrada se aproximam de zero do lado esquerdo (tornando-se valores muito pequenos e negativos), os valores da função diminuem sem limite (em outras palavras, eles se aproximam do infinito negativo). Podemos ver esse comportamento na Tabela\(\PageIndex{2}\).
| \(x\) | —0,1 | —0,01 | —0,001 | —0,0001 |
|---|---|---|---|---|
| \(f(x)=\frac{1}{x}\) | —10 | —100 | —1000 | —10.000 |
Nós escrevemos em notação de seta
À medida que os valores de entrada se aproximam de zero do lado direito (tornando-se valores muito pequenos e positivos), os valores da função aumentam sem limite (aproximando-se do infinito). Podemos ver esse comportamento na Tabela\(\PageIndex{3}\).
| \(x\) | 0.1 | 0,01 | 0,001 | 0,0001 |
|---|---|---|---|---|
| \(f(x)=\frac{1}{x}\) | 10 | 100 | 1000 | 10.000 |
Nós escrevemos em notação de seta
Veja a Figura\(\PageIndex{2}\).
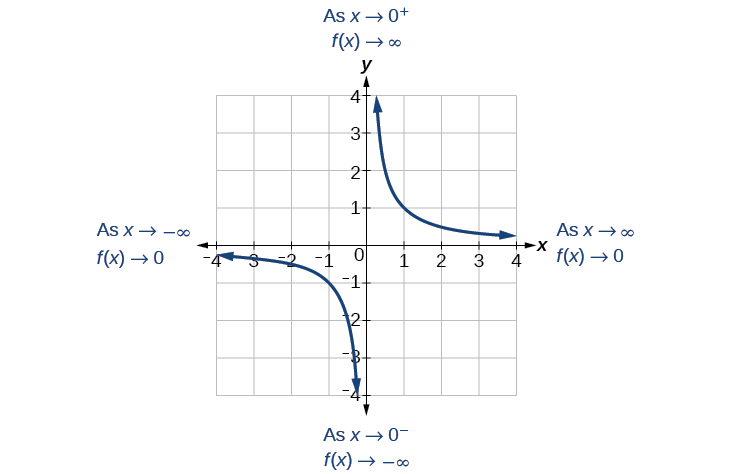
Esse comportamento cria uma assíntota vertical, que é uma linha vertical que o gráfico se aproxima, mas nunca cruza. Nesse caso, o gráfico está se aproximando da linha vertical à\(x=0\) medida que a entrada se aproxima de zero (Figura\(\PageIndex{3}\)).
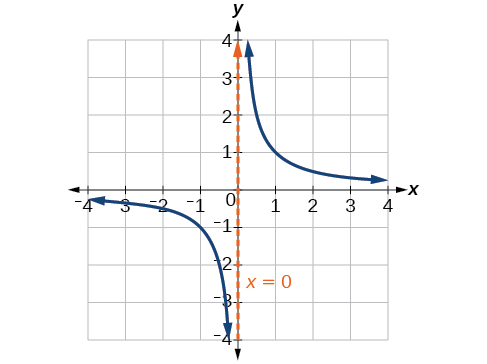
Definição: ASSÍNTOTA VERTICAL
Uma assíntota vertical de um gráfico é uma linha vertical em\(x=a\) que o gráfico tende para o infinito positivo ou negativo à medida que as entradas se aproximam\(a\). Nós escrevemos
Como\(x\rightarrow a\)\(f(x)\rightarrow \infty\), ou como\(x\rightarrow a\),\(f(x)\rightarrow −\infty\).Comportamento final de\(f(x)=\frac{1}{x}\)
À medida que os valores\(x\) se aproximam do infinito, os valores da função se aproximam\(0\). À medida que os valores\(x\) se aproximam do infinito negativo, os valores da função se aproximam\(0\) (Figura\(\PageIndex{4}\)). Simbolicamente, usando a notação de seta
Como\(x\rightarrow \infty\)\(f(x)\rightarrow 0\), e como\(x\rightarrow −\infty\),\(f(x)\rightarrow 0\).
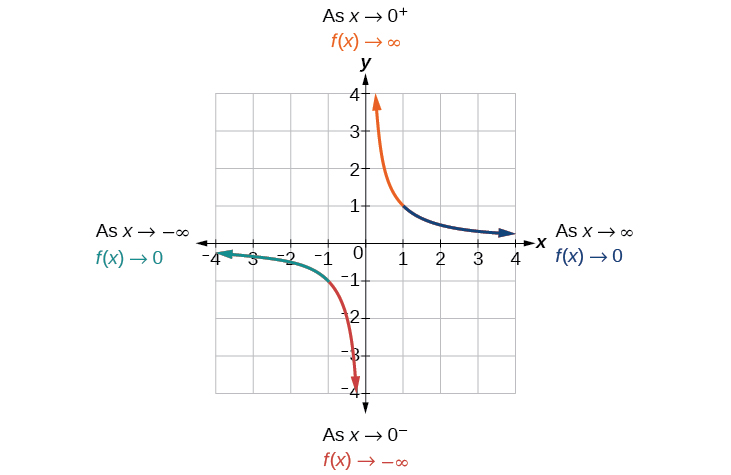
Com base nesse comportamento geral e no gráfico, podemos ver que a função se aproxima de 0, mas nunca chega a 0; parece se estabilizar à medida que as entradas se tornam grandes. Esse comportamento cria uma assíntota horizontal, uma linha horizontal da qual o gráfico se aproxima à medida que a entrada aumenta ou diminui sem limite. Nesse caso, o gráfico está se aproximando da linha horizontal\(y=0\). Veja a Figura\(\PageIndex{5}\).
Definição: ASSÍNTOTA HORIZONTAL
Uma assíntota horizontal de um gráfico é uma linha horizontal em\(y=b\) que o gráfico se aproxima da linha à medida que as entradas aumentam ou diminuem sem limite. Nós escrevemos
Exemplo\(\PageIndex{1}\): Using Arrow Notation.
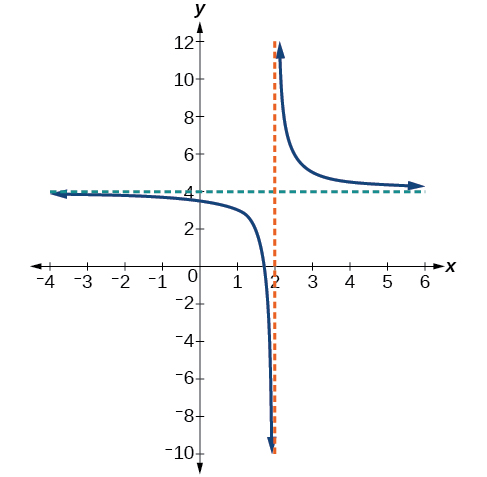
Use a notação de seta para descrever o comportamento final e o comportamento local da função representada graficamente na Figura\(\PageIndex{6}\).
Solução
Observe que o gráfico está mostrando uma assíntota vertical em\(x=2\), o que nos diz que a função é indefinida em\(x=2\).
E à medida que as entradas diminuem sem limite, o gráfico parece estar se nivelando nos valores de saída de\(4\), indicando uma assíntota horizontal em\(y=4\). À medida que as entradas aumentam sem limite, o gráfico se estabiliza em\(4\).
Exercícios\(\PageIndex{1}\)
Use a notação de seta para descrever o comportamento final e o comportamento local da função quadrada recíproca.
- Responda
-
Comportamento final: como\(x\rightarrow \pm \infty\),\(f(x)\rightarrow 0\);
Comportamento local: como\(x\rightarrow 0\),\(f(x)\rightarrow \infty\) (não há interceptações x ou y)
Exemplo\(\PageIndex{2}\): Using Transformations to Graph a Rational Function.
Esboce um gráfico da função recíproca deslocada duas unidades para a esquerda e três unidades para cima. Identifique as assíntotas horizontais e verticais do gráfico, se houver.
Solução
Deslocar o gráfico para a esquerda 2 e para cima 3 resultaria na função
\[f(x)=\dfrac{1}{x+2}+3\]
ou equivalentemente, dando aos termos um denominador comum,
\[f(x)=\dfrac{3x+7}{x+2}\]
O gráfico da função deslocada é exibido na Figura\(\PageIndex{7}\).
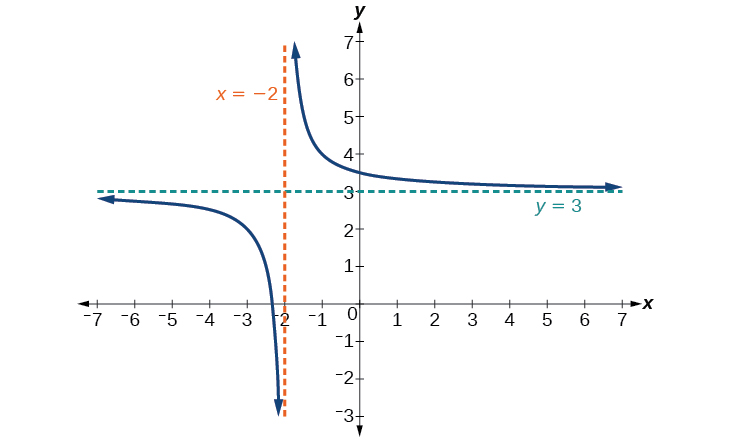
Observe que essa função é indefinida em\(x=−2\), e o gráfico também mostra uma assíntota vertical em\(x=−2\).
À medida que as entradas aumentam e diminuem sem limite, o gráfico parece estar se nivelando em valores de saída de 3, indicando uma assíntota horizontal em\(y=3\).
Análise
Observe que as assíntotas horizontais e verticais são deslocadas para a esquerda 2 e para cima 3 junto com a função.
Exercício\(\PageIndex{2}\)
Desenhe o gráfico e encontre as assíntotas horizontais e verticais da função quadrada recíproca que foi deslocada para a direita 3 unidades e para baixo 4 unidades.
Solução
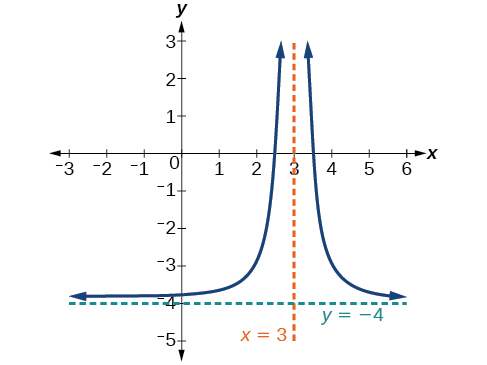
A função e as assíntotas são deslocadas 3 unidades para a direita e 4 unidades para baixo. Como\(x\rightarrow 3\), \(f(x)\rightarrow \infty\), and as \(x\rightarrow \pm \infty\), \(f(x)\rightarrow −4\).
A função é\(f(x)=\frac{1}{{(x−3)}^2}−4\).
Resolvendo problemas aplicados envolvendo funções racionais
No exemplo\(\PageIndex{2}\), mudamos uma função do kit de ferramentas de uma forma que resultou na função\(f(x)=\frac{3x+7}{x+2}\). Esse é um exemplo de função racional. Uma função racional é uma função que pode ser escrita como o quociente de duas funções polinomiais. Muitos problemas do mundo real exigem que encontremos a proporção de duas funções polinomiais. Problemas envolvendo taxas e concentrações geralmente envolvem funções racionais.
Definição: FUNÇÃO RACIONAL
Uma função racional é uma função que pode ser escrita como o quociente de duas funções polinomiais\(P(x)\)\(Q(x)\) e.
\[f(x)=\dfrac{P(x)}{Q(x)}=\dfrac{a_px^p+a_{p−1}x^{p−1}+...+a_1x+a_0}{b_qx^q+b_{q−1}x^{q−1}+...+b_1x+b_0},\space Q(x)≠0\]Exemplo\(\PageIndex{3}\): Solving an Applied Problem Involving a Rational Function
Atualmente, um grande tanque de mistura contém 100 galões de água nos quais 5 libras de açúcar foram misturadas. Uma torneira se abrirá despejando 10 galões por minuto de água no tanque ao mesmo tempo em que o açúcar é despejado no tanque a uma taxa de 1 libra por minuto. Encontre a concentração (libras por galão) de açúcar no tanque após 12 minutos. Essa é uma concentração maior do que no início?
Solução
Seja o número de minutos desde que a torneira abriu. Como a água aumenta a 10 galões por minuto e o açúcar aumenta a 1 libra por minuto, essas são taxas de variação constantes. Isso nos diz que a quantidade de água no tanque está mudando linearmente, assim como a quantidade de açúcar no tanque. Podemos escrever uma equação de forma independente para cada uma:
A concentração,\(C\), será a proporção de libras de açúcar para galões de água
\[C(t)=\dfrac{5+t}{100+10t}\]
A concentração após 12 minutos é dada avaliando\(C(t)\) em\(t= 12\).
\[\begin{align} C(12) & =\dfrac{5+12}{100+10(12)} \\ &= \dfrac{17}{220} \end{align} \]
Isso significa que a concentração é de 17 libras de açúcar para 220 galões de água.
No início, a concentração é
\[\begin{align} C(0) & =\dfrac{5+0}{100+10(0)} \\ & =\dfrac{1}{20} \end{align} \]
Pois\(\frac{17}{220}≈0.08>\frac{1}{20}=0.05\), a concentração é maior após 12 minutos do que no início.
Análise
Para encontrar a assíntota horizontal, divida o coeficiente principal no numerador pelo coeficiente principal no denominador:
\[\dfrac{1}{10}=0.1\]
Observe que a assíntota horizontal é\(y= 0.1.\) Isso significa que a concentração,\(C,\) a proporção de libras de açúcar para galões de água, se aproximará de 0,1 a longo prazo.
Exercício\(\PageIndex{3}\)
Há 1.200 calouros e 1.500 alunos do segundo ano em um comício preparatório ao meio-dia. Depois das 12h, 20 calouros chegam ao comício a cada cinco minutos, enquanto 15 alunos do segundo ano saem do comício. Encontre a proporção de calouros para alunos do segundo ano às 13h.
- Responda
-
\(\frac{12}{11}\)
Encontrando os domínios das funções racionais
Uma assíntota vertical representa um valor no qual uma função racional é indefinida, então esse valor não está no domínio da função. Uma função recíproca não pode ter valores em seu domínio que façam com que o denominador seja igual a zero. Em geral, para encontrar o domínio de uma função racional, precisamos determinar quais entradas causariam a divisão por zero.
Definição: DOMÍNIO DE UMA FUNÇÃO RACIONAL
O domínio de uma função racional inclui todos os números reais, exceto aqueles que fazem com que o denominador seja igual a zero.
Como fazer: Dada uma função racional, encontre o domínio.
- Defina o denominador igual a zero.
- Resolva para encontrar os valores de x que fazem com que o denominador seja igual a zero.
- O domínio contém todos os números reais, exceto aqueles encontrados na Etapa 2.
Exemplo\(\PageIndex{4}\): Finding the Domain of a Rational Function
Encontre o domínio de\(f(x)=\dfrac{x+3}{x^2−9}\).
Solução
Comece definindo o denominador igual a zero e resolvendo.
\[x^2-9=0 \nonumber \]
\[x^2=9 \nonumber \]\[x=\pm 3 \nonumber \]
O denominador é igual a zero quando\(x=\pm 3\). O domínio da função é composto por todos os números reais, exceto\(x=\pm 3\).
Análise
Um gráfico dessa função, conforme mostrado na Figura\(\PageIndex{9}\), confirma que a função não está definida quando\(x=\pm 3\).
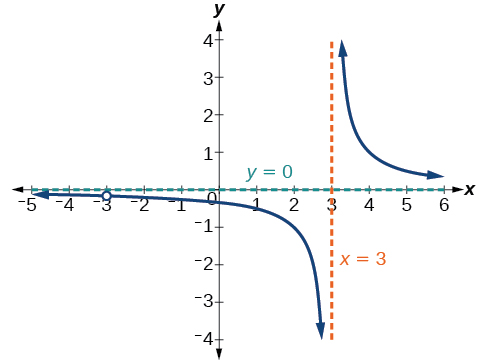
Há uma assíntota vertical em\(x=3\) e um orifício no gráfico em\(x=−3\). Discutiremos esses tipos de furos com mais detalhes posteriormente nesta seção.
Exercício\(\PageIndex{4}\)
Encontre o domínio de\(f(x)=\dfrac{4x}{5(x−1)(x−5)}\).
- Responda
-
O domínio é composto por todos números reais, exceto\(x=1\)\(x=5\) e.
Identificação de assíntotas verticais de funções racionais
Ao observar o gráfico de uma função racional, podemos investigar seu comportamento local e ver facilmente se há assíntotas. Talvez até consigamos aproximar sua localização. Mesmo sem o gráfico, no entanto, ainda podemos determinar se uma determinada função racional tem alguma assíntota e calcular sua localização.
Assíntotas verticais
As assíntotas verticais de uma função racional podem ser encontradas examinando os fatores do denominador que não são comuns aos fatores no numerador. As assíntotas verticais ocorrem nos zeros desses fatores.
Como fazer: Dada uma função racional, identifique quaisquer assíntotas verticais de seu gráfico
- Fator o numerador e o denominador.
- Observe todas as restrições no domínio da função.
- Reduza a expressão cancelando fatores comuns no numerador e no denominador.
- Observe todos os valores que fazem com que o denominador seja zero nesta versão simplificada. É aqui que ocorrem as assíntotas verticais.
- Observe todas as restrições no domínio em que as assíntotas não ocorrem. Essas são descontinuidades removíveis ou “furos”.
Exemplo\(\PageIndex{5}\): Identifying Vertical Asymptotes
Encontre as assíntotas verticais do gráfico de\(k(x)=\dfrac{5+2x^2}{2−x−x^2}\).
Solução
Primeiro, fatore o numerador e o denominador.
\[k(x)=\dfrac{5+2x^2}{2−x−x^2} \nonumber \]
\[=\dfrac{5+2x^2}{(2+x)(1-x)} \nonumber \]
Para encontrar as assíntotas verticais, determinamos onde essa função será indefinida definindo o denominador igual a zero:
\[(2+x)(1−x)=0 \nonumber \]
\[x=−2, \; x=1 \nonumber \]
\(x=–2\)Nem\(x=1\) os zeros do numerador, então os dois valores indicam duas assíntotas verticais. O gráfico na Figura\(\PageIndex{10}\) confirma a localização das duas assíntotas verticais.
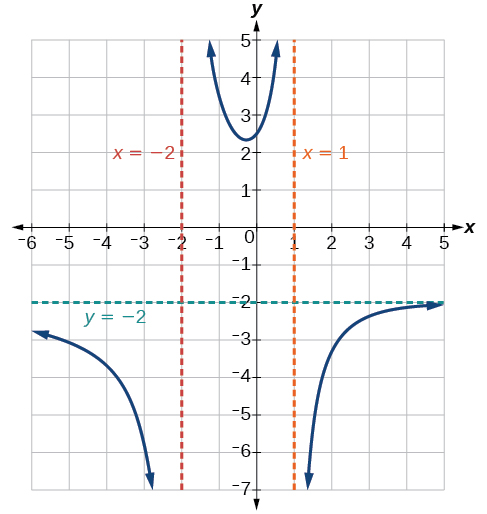
Descontinuidades removíveis
Ocasionalmente, um gráfico conterá um furo: um único ponto onde o gráfico não está definido, indicado por um círculo aberto. Chamamos esse buraco de descontinuidade removível. Por exemplo, a função\(f(x)=\dfrac{x^2−1}{x^2−2x−3}\) pode ser reescrita fatorando o numerador e o denominador.
Observe que\(x+1\) é um fator comum ao numerador e ao denominador. O zero desse fator,\(x=−1\), é a localização da descontinuidade removível. Observe também que isso não\( (x–3) \) é um fator tanto no numerador quanto no denominador. O zero desse fator,\(x=3\), é a assíntota vertical. Veja a Figura\(\PageIndex{11}\). [Observe que as descontinuidades removíveis podem não ser visíveis quando usamos uma calculadora gráfica, dependendo da janela selecionada.]
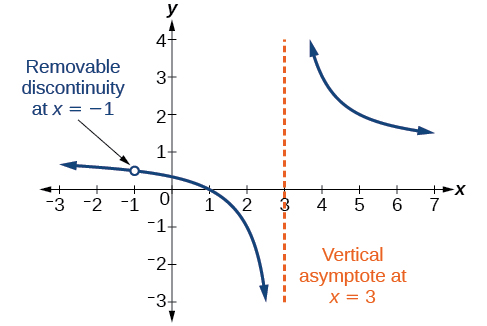
DESCONTINUIDADES REMOVÍVEIS DE FUNÇÕES RACIONAIS
Uma descontinuidade removível ocorre no gráfico de uma função racional em\(x=a\) se\(a\) for zero para um fator no denominador que é comum a um fator no numerador. Fatoramos o numerador e o denominador e verificamos fatores comuns. Se encontrarmos algum, definimos o fator comum igual a 0 e resolvemos. Esse é o local da descontinuidade removível. Isso é verdade se a multiplicidade desse fator for maior ou igual à do denominador. Se a multiplicidade desse fator for maior no denominador, ainda haverá uma assíntota nesse valor.
Exemplo\(\PageIndex{6}\): Identifying Vertical Asymptotes and Removable Discontinuities for a Graph
Encontre as assíntotas verticais e as descontinuidades removíveis do gráfico de\(k(x)=\dfrac{x−2}{x^2−4}\).
Solução
Fator o numerador e o denominador.
\[k(x)=\dfrac{x−2}{(x−2)(x+2)} \nonumber \]
Observe que há um fator comum no numerador e no denominador,\(x–2\). O zero para esse fator é\(x=2\). Esse é o local da descontinuidade removível.
Observe que há um fator no denominador que não está no numerador,\(x+2\). O zero para esse fator é\(x=−2\). A assíntota vertical é\(x=−2\). Veja a Figura\(\PageIndex{12}\).
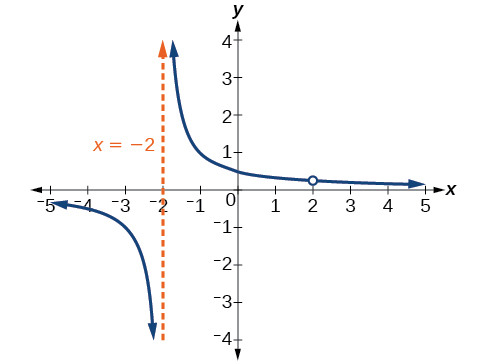
O gráfico dessa função terá a assíntota vertical em\(x=−2\), mas\(x=2\) no gráfico terá um furo.
Exercício\(\PageIndex{5}\)
Encontre as assíntotas verticais e as descontinuidades removíveis do gráfico de\(f(x)=\dfrac{x^2−25}{x^3−6x^2+5x}\).
- Responda
-
Descontinuidade removível em\(x=5\).
Assíntotas verticais:\(x=0\),\(x=1\).
Identificação de assíntotas horizontais de funções racionais
Enquanto as assíntotas verticais descrevem o comportamento de um gráfico à medida que a saída fica muito grande ou muito pequena, as assíntotas horizontais ajudam a descrever o comportamento de um gráfico à medida que a entrada fica muito grande ou muito pequena. Lembre-se de que o comportamento final de um polinômio refletirá o do termo principal. Da mesma forma, o comportamento final de uma função racional refletirá o da razão da função que é a razão dos termos principais.
Há três resultados distintos na verificação de assíntotas horizontais:
Caso 1: Se o grau do denominador > grau do numerador, há uma assíntota horizontal em\(y=0\).
Nesse caso, o comportamento final é\(f(x)≈\dfrac{4x}{x^2}=\dfrac{4}{x}\). Isso nos diz que, à medida que as entradas aumentam ou diminuem sem limite, essa função se comportará de forma semelhante à função\(g(x)=\dfrac{4}{x}\), e as saídas se aproximarão de zero, resultando em uma assíntota horizontal em\(y=0\). Veja a Figura\(\PageIndex{13}\). Observe que esse gráfico cruza a assíntota horizontal.
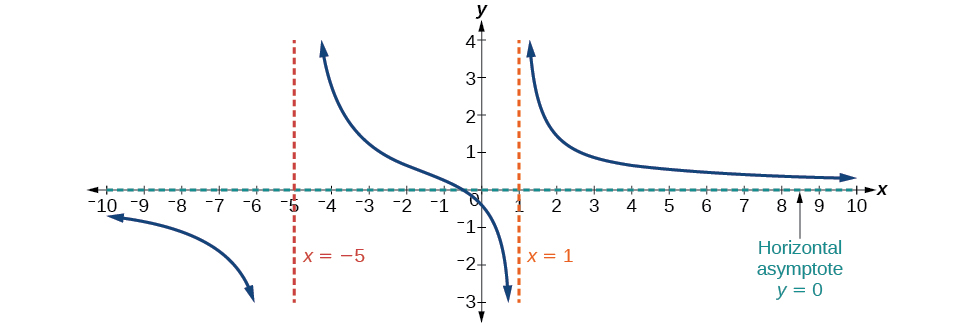
Figura\(\PageIndex{13}\): Assíntota horizontal\(y=0\) quando\(f(x)=\dfrac{p(x)}{q(x)}\),\(q(x)≠0\) onde grau de\(p\) < grau de\(q\).
Caso 2: Se o grau do denominador < grau do numerador em um, obtemos uma assíntota inclinada.
Nesse caso, o comportamento final é\(f(x)≈\dfrac{3x^2}{x}=3x\). Isso nos diz que, à medida que as entradas aumentam ou diminuem sem limite, essa função se comportará de forma semelhante à função\(g(x)=3x\). À medida que as entradas aumentam, as saídas aumentam e não se nivelam, portanto, esse gráfico não tem assíntota horizontal. No entanto, o gráfico de\(g(x)=3x\) parece uma linha diagonal e, como se\(f\) comportará de forma semelhante\(g\), ele se aproximará de uma linha próxima\(y=3x\) a. Essa linha é uma assíntota inclinada.
Para encontrar a equação da assíntota inclinada, divida\(\dfrac{3x^2−2x+1}{x−1}\). O quociente é\(3x+1\), e o restante é 2. A assíntota inclinada é o gráfico da linha\(g(x)=3x+1\). Veja a Figura\(\PageIndex{14}\).
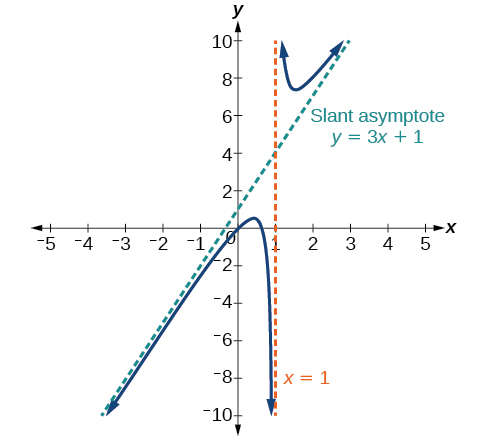
Figura\(\PageIndex{14}\): Assíntota inclinada quando\(f(x)=\dfrac{p(x)}{q(x)}\),\(q(x)≠0\) onde grau de\(p\) >grau de\(q\) por 1.
Caso 3: Se o grau do denominador = grau do numerador, há uma assíntota horizontal em\(y=\dfrac{a_n}{b_n}\), onde\(a_n\) e\(b_n\) são respectivamente os coeficientes principais de\(p(x)\) e\(q(x)\) para\(f(x)=\dfrac{p(x)}{q(x)}\),\(q(x)≠0\).
Nesse caso, o comportamento final é\(f(x)≈\dfrac{3x^2}{x^2}=3\). Isso nos diz que, à medida que as entradas aumentam, essa função se comportará como a função\(g(x)=3\), que é uma linha horizontal. Como\(x\rightarrow \pm \infty\)\(f(x)\rightarrow 3\), resultando em uma assíntota horizontal em\(y=3\). Veja a Figura\(\PageIndex{15}\). Observe que esse gráfico cruza a assíntota horizontal.
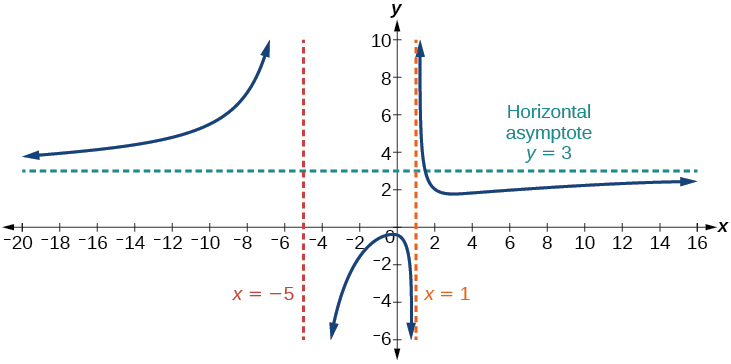
Figura\(\PageIndex{15}\): Assíntota horizontal quando\(f(x)=\dfrac{p(x)}{q(x)}\),\(q(x)≠0\) onde grau de\(p\) = grau de\(q\).
Observe que, embora o gráfico de uma função racional nunca cruze uma assíntota vertical, o gráfico pode ou não cruzar uma assíntota horizontal ou inclinada. Além disso, embora o gráfico de uma função racional possa ter muitas assíntotas verticais, o gráfico terá no máximo uma assíntota horizontal (ou inclinada).
Deve-se notar que, se o grau do numerador for maior que o grau do denominador em mais de um, o comportamento final do gráfico imitará o comportamento da fração reduzida do comportamento final. Por exemplo, se tivéssemos a função
\[f(x)=\dfrac{3x^5−x^2}{x+3} \nonumber \]
com comportamento final
\[f(x)≈\dfrac{3x^5}{x}=3x^4 \nonumber \]
o comportamento final do gráfico seria semelhante ao de um polinômio par com um coeficiente inicial positivo.
ASSÍNTOTAS HORIZONTAIS DE FUNÇÕES RACIONAIS
A assíntota horizontal de uma função racional pode ser determinada observando os graus do numerador e do denominador.
- O grau do numerador é menor que o grau do denominador: assíntota horizontal em\(y=0\).
- O grau do numerador é maior do que o grau do denominador em um: sem assíntota horizontal; assíntota inclinada.
- O grau do numerador é igual ao grau do denominador: assíntota horizontal na proporção dos coeficientes principais.
Exemplo\(\PageIndex{7}\): Identifying Horizontal and Slant Asymptotes
Para as funções listadas, identifique a assíntota horizontal ou inclinada.
- \(g(x)=\dfrac{6x^3−10x}{2x^3+5x^2}\)
- \(h(x)=\dfrac{x^2−4x+1}{x+2}\)
- \(k(x)=\dfrac{x^2+4x}{x^3−8}\)
Solução
Para essas soluções, usaremos\(f(x)=\dfrac{p(x)}{q(x)},\space q(x)≠0\).
- \(g(x)=\dfrac{6x^3−10x}{2x^3+5x^2}\): O grau de\(p = \) grau de\(q=3\), para que possamos encontrar a assíntota horizontal tomando a proporção dos termos principais. Há uma assíntota horizontal em\(y =\frac{6}{2}\) ou\(y=3\).
- \(h(x)=\dfrac{x^2−4x+1}{x+2}\): O grau\(p=2\) e o grau de\(q=1\). Desde\(p>q\) 1, há uma assíntota inclinada encontrada em\(\dfrac{x^2−4x+1}{x+2}\).
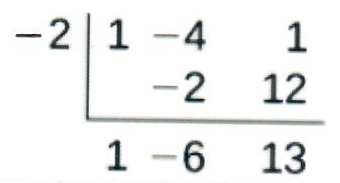
- \(k(x)=\dfrac{x^2+4x}{x^3−8}\): O grau de\(p=2\) < grau de\(q=3\), então há uma assíntota horizontal\(y=0\).
Exemplo\(\PageIndex{8}\) Identifying Horizontal Asymptotes
Encontre a assíntota horizontal e interprete-a no contexto do problema.
Solução
Tanto o numerador quanto o denominador são lineares (grau 1). Como os graus são iguais, haverá uma assíntota horizontal na proporção dos coeficientes principais. No numerador, o termo principal é\(t\), com coeficiente 1. No denominador, o termo principal é 10t, com coeficiente 10. A assíntota horizontal estará na proporção desses valores:
Essa função terá uma assíntota horizontal em\(y=\frac{1}{10}\).
Isso nos diz que, à medida que os valores de\(t\) aumentam, os valores da\(C\) vontade se aproximam\(\frac{1}{10}\). No contexto, isso significa que, com o passar do tempo, a concentração de açúcar no tanque se aproximará de um décimo de libra de açúcar por galão de água ou\(\frac{1}{10}\) libras por galão.
Exemplo\(\PageIndex{9}\): Identifying Horizontal and Vertical Asymptotes
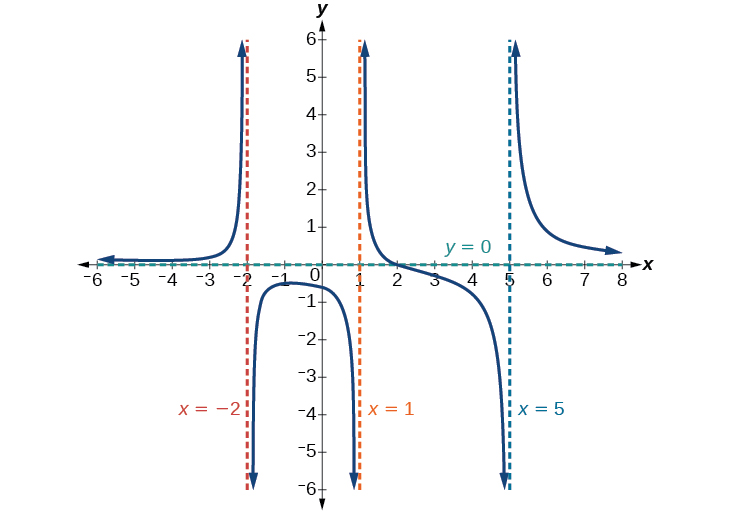
Encontre as assíntotas horizontal e vertical da função\(f(x)=\dfrac{(x−2)(x+3)}{(x−1)(x+2)(x−5)}\)
Primeiro, observe que essa função não tem fatores comuns, portanto, não há possíveis descontinuidades removíveis.
A função terá assíntotas verticais quando o denominador for zero, fazendo com que a função seja indefinida. O denominador será zero em\(x=1,–2,\) e\(5\), indicando assíntotas verticais nesses valores.
O numerador tem grau\(2\), enquanto o denominador tem grau 3. Como o grau do denominador é maior que o grau do numerador, o denominador crescerá mais rápido que o numerador, fazendo com que as saídas tendam para zero à medida que as entradas aumentam, e assim\(x\rightarrow \pm \infty\) por diante\(f(x)\rightarrow 0\). Esta função terá uma assíntota horizontal em\(y =0.\) See Figure\(\PageIndex{16}\).
Exercício\(\PageIndex{6}\)
Encontre as assíntotas verticais e horizontais da função:
\(f(x)=\dfrac{(2x−1)(2x+1)}{(x−2)(x+3)}\)
- Responda
-
Assíntotas verticais em\(x=2\) e\(x=–3\)
assíntota horizontal em\(y =4\).
INTERCEPTAÇÕES DE FUNÇÕES RACIONAIS
Uma função racional terá um\(y\) intercepto -em\(f(0),\) se a função for definida em zero. Uma função racional não terá um\(y\) intercepto -se a função não estiver definida em zero.
Da mesma forma, uma função\(x\) racional terá interceptações nas entradas que fazem com que a saída seja zero. Como uma fração só é igual a zero quando o numerador é zero, as interceptações x só podem ocorrer quando o numerador da função racional é igual a zero.
Exemplo\(\PageIndex{10}\): Finding the Intercepts of a Rational Function
Encontre as interceptações de \(f(x)=\dfrac{(x−2)(x+3)}{(x−1)(x+2)(x−5)}\).
Solução
Podemos encontrar o intercepto y avaliando a função em zero
As interceptações x ocorrerão quando a função for igual a zero:
\[ 0=(x−2)(x+3) \qquad \qquad \qquad \qquad \qquad \nonumber \]
\[ x=2, x=−3 \qquad \qquad \qquad \qquad \qquad \nonumber \]
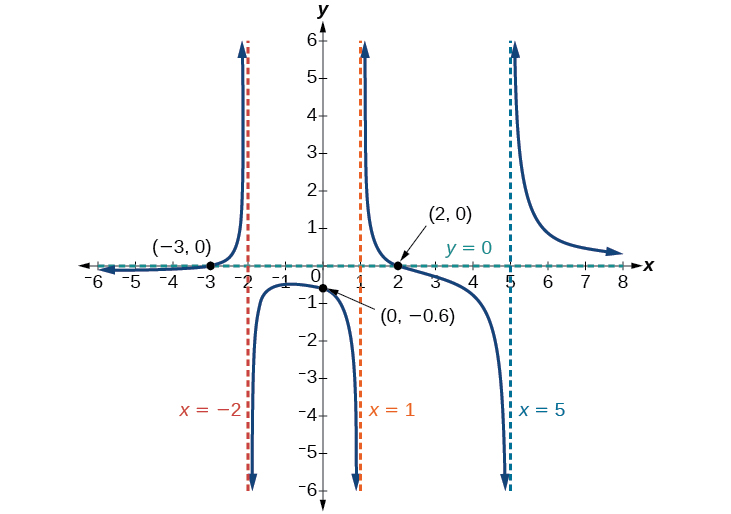
O intercepto y é\((0,–0.6)\), os interceptos x são\((2,0)\)\((–3,0)\) e. Veja a Figura\(\PageIndex{17}\).
Exercício\(\PageIndex{7}\)
Dada a função quadrada recíproca que é deslocada para a direita 3 unidades e para baixo 4 unidades, escreva isso como uma função racional. Em seguida, encontre as interceptações x e y e as assíntotas horizontal e vertical.
- Responda
-
Para a função quadrada recíproca transformada, encontramos a forma racional.
\(f(x)=\dfrac{1}{{(x−3)}^2}−4=\dfrac{1−4{(x−3)}^2}{{(x−3)}^2}=\dfrac{1−4(x^2−6x+9)}{(x−3)(x−3)}=\dfrac{−4x^2+24x−35}{x^2−6x+9}\)
Como o numerador tem o mesmo grau do denominador, sabemos que\(x\rightarrow \pm \infty\),\(f(x)\rightarrow −4\); assim como\(y=–4\) a assíntota horizontal. Em seguida, definimos o denominador igual a zero e descobrimos que a assíntota vertical é\(x=3\), porque como\(x\rightarrow 3\),\(f(x)\rightarrow \infty\). Em seguida, definimos o numerador igual a\(0\) e descobrimos que os interceptos x estão em\((2.5,0)\)\((3.5,0)\) e. Finalmente, calculamos a função em 0 e descobrimos que o intercepto y está em\((0,−\frac{35}{9})\).
Representação gráfica de funções racionais
No exemplo\(\PageIndex{10}\), vemos que o numerador de uma função racional revela os interceptos x do gráfico, enquanto o denominador revela as assíntotas verticais do gráfico. Assim como acontece com os polinômios, os fatores do numerador podem ter potências inteiras maiores que um. Felizmente, o efeito na forma do gráfico nessas interceptações é o mesmo que vimos com os polinômios.
As assíntotas verticais associadas aos fatores do denominador refletirão uma das duas funções recíprocas do kit de ferramentas. Quando o grau do fator no denominador é ímpar, a característica distintiva é que, em um lado da assíntota vertical, o gráfico se dirige para o infinito positivo e, do outro lado, o gráfico segue para o infinito negativo. Veja a Figura\(\PageIndex{18}\).
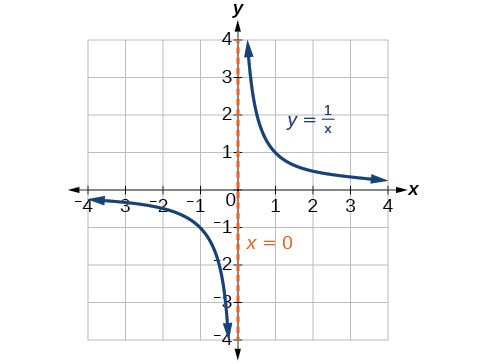
Quando o grau do fator no denominador é par, a característica distintiva é que o gráfico avança em direção ao infinito positivo em ambos os lados da assíntota vertical ou segue em direção ao infinito negativo em ambos os lados. Veja a Figura\(\PageIndex{19}\).
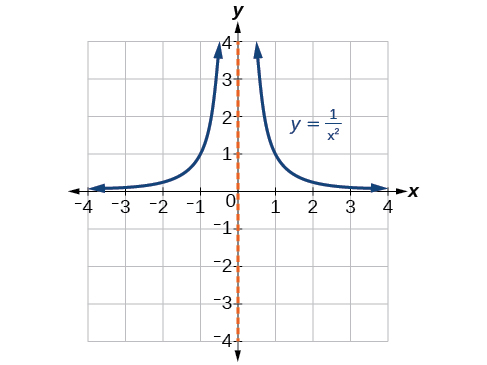
Por exemplo, o gráfico de \(f(x)=\dfrac{{(x+1)}^2(x−3)}{{(x+3)}^2(x−2)}\)é mostrado na Figura\(\PageIndex{20}\).

- No intercepto x\(x=−1\) correspondente ao\({(x+1)}^2\) fator do numerador, o gráfico “salta”, consistente com a natureza quadrática do fator.
- No intercepto x\(x=3\) correspondente ao\((x−3)\) fator do numerador, o gráfico passa pelo eixo como esperaríamos de um fator linear.
- Na assíntota vertical\(x=−3\) correspondente ao\({(x+3)}^2\) fator do denominador, o gráfico segue em direção ao infinito positivo em ambos os lados da assíntota, consistente com o comportamento da função\(f(x)=\dfrac{1}{x^2}\).
- Na assíntota vertical\(x=2\), correspondente ao\((x−2)\) fator do denominador, o gráfico segue para o infinito positivo no lado esquerdo da assíntota e para o infinito negativo no lado direito, consistente com o comportamento da função\(f(x)=\dfrac{1}{x}\).
Como fazer: Dada uma função racional, esboce um gráfico.
- Avalie a função em 0 para encontrar o intercepto y.
- Fator o numerador e o denominador.
- Para fatores no numerador não comuns ao denominador, determine onde cada fator do numerador é zero para encontrar os interceptos x.
- Encontre as multiplicidades dos interceptos x para determinar o comportamento do gráfico nesses pontos.
- Para fatores no denominador, observe as multiplicidades dos zeros para determinar o comportamento local. Para aqueles fatores não comuns ao numerador, encontre as assíntotas verticais definindo esses fatores iguais a zero e depois resolva.
- Para fatores no denominador comuns aos fatores no numerador, encontre as descontinuidades removíveis definindo esses fatores iguais a 0 e resolva.
- Compare os graus do numerador e do denominador para determinar as assíntotas horizontais ou inclinadas.
- Esboce o gráfico.
Exemplo\(\PageIndex{11}\): Graphing a Rational Function
Esboce um gráfico de\(f(x)=\frac{(x+2)(x−3)}{{(x+1)}^2(x−2)}\).
Solução
Podemos começar observando que a função já está fatorada, economizando uma etapa.
Em seguida, encontraremos as interceptações. Avaliar a função em zero fornece o intercepto y:
Para encontrar os interceptos x, determinamos quando o numerador da função é zero. Definindo cada fator igual a zero, encontramos interceptos x em\(x=–2\)\(x=3\) e. Em cada um, o comportamento será linear (multiplicidade 1), com o gráfico passando pelo intercepto.
Temos um intercepto y em\((0,3)\) e intercepta x em\((–2,0)\)\((3,0)\) e.
Para encontrar as assíntotas verticais, determinamos quando o denominador é igual a zero. Isso ocorre quando\(x+1=0\) e quando\(x–2=0\), nos dando assíntotas verticais em\(x=–1\)\(x=2\) e.
Não há fatores comuns no numerador e no denominador. Isso significa que não há descontinuidades removíveis.
Finalmente, o grau do denominador é maior que o grau do numerador, nos dizendo que este gráfico tem uma assíntota horizontal em\(y =0\).
Para esboçar o gráfico, podemos começar traçando as três interceptações. Como o gráfico não tem interceptos x entre as assíntotas verticais e o intercepto y é positivo, sabemos que a função deve permanecer positiva entre as assíntotas, permitindo preencher a parte central do gráfico, conforme mostrado na Figura\(\PageIndex{21}\).
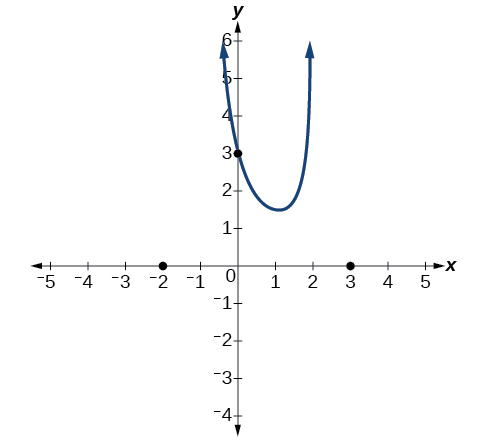
O fator associado à assíntota vertical at\(x=−1\) foi quadrado, então sabemos que o comportamento será o mesmo em ambos os lados da assíntota. O gráfico segue em direção ao infinito positivo à medida que as entradas se aproximam da assíntota à direita, então o gráfico também se dirige para o infinito positivo à esquerda.
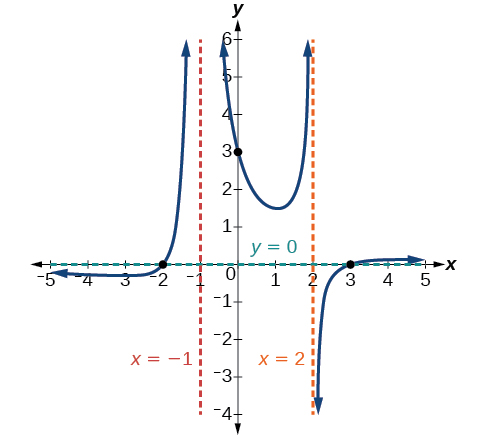
Para a assíntota vertical em\(x=2\), o fator não foi quadrado, então o gráfico terá um comportamento oposto em ambos os lados da assíntota. Veja a Figura\(\PageIndex{22}\). Depois de passar pelas interceptações x, o gráfico então se nivelará em direção a uma saída de zero, conforme indicado pela assíntota horizontal.
Exercício\(\PageIndex{8}\)
Dada a função\(f(x)=\frac{{(x+2)}^2(x−2)}{2{(x−1)}^2(x−3)}\), use as características de polinômios e funções racionais para descrever seu comportamento e esboçar a função.
- Responda
-
Assíntota horizontal em\(y=\frac{1}{2}\). Assíntotas verticais em\(x=1\)\(x=3\) e. intercepto y em\((0,\frac{4}{3})\).
x intercepta em\((2,0)\)\((–2,0)\) e. \((–2,0)\)é um zero com multiplicidade\(2\), e o gráfico salta do eixo x nesse ponto. \((2,0)\)é um único zero e o gráfico cruza o eixo nesse ponto.

Figura\(\PageIndex{23}\).
Escrevendo funções racionais
Agora que analisamos as equações para funções racionais e como elas se relacionam com um gráfico da função, podemos usar as informações fornecidas por um gráfico para escrever a função. Uma função racional escrita em forma fatorada terá um intercepto x em que cada fator do numerador é igual a zero. (Uma exceção ocorre no caso de uma descontinuidade removível.) Como resultado, podemos formar um numerador de uma função cujo gráfico passará por um conjunto de interceptos x introduzindo um conjunto correspondente de fatores. Da mesma forma, como a função terá uma assíntota vertical em que cada fator do denominador é igual a zero, podemos formar um denominador que produzirá as assíntotas verticais introduzindo um conjunto correspondente de fatores.
ESCREVER FUNÇÕES RACIONAIS A PARTIR DE INTERCEPTAÇÕES E ASSÍNTOTAS
Se uma função racional tem interceptos x em\(x=x_1,x_2,...,x_n\), assíntotas verticais em\(x=v_1,v_2,…,v_m\) e\(x_i=\) nenhuma\(v_j\), então a função pode ser escrita na forma:
onde as potências\(p_i\) ou\(q_i\) em cada fator podem ser determinadas pelo comportamento do gráfico na interceptação ou assíntota correspondente, e o fator de estiramento\(a\) pode ser determinado dado um valor da função diferente do intercepto x ou pela assíntota horizontal se for diferente de zero.
Dado um gráfico de uma função racional, escreva a função.
- Determine os fatores do numerador. Examine o comportamento do gráfico nas interceptações x para determinar os zeros e suas multiplicidades. (Isso é fácil de fazer ao encontrar a função “mais simples” com multiplicidades pequenas, como 1 ou 3, mas pode ser difícil para multiplicidades maiores, como 5 ou 7, por exemplo.)
- Determine os fatores do denominador. Examine o comportamento em ambos os lados de cada assíntota vertical para determinar os fatores e seus poderes.
- Use qualquer ponto claro no gráfico para encontrar o fator de estiramento.
Exemplo\(\PageIndex{12}\): Writing a Rational Function from Intercepts and Asymptotes
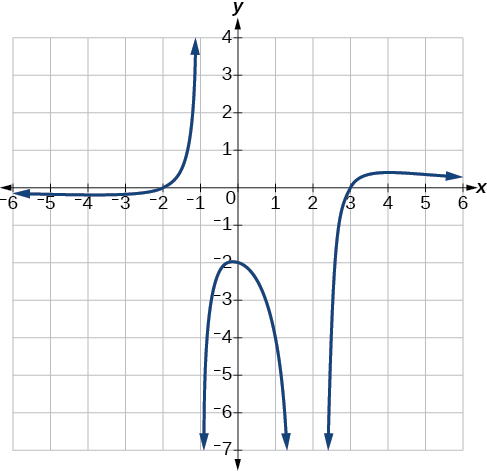
Escreva uma equação para a função racional mostrada na Figura\(\PageIndex{24}\).
Solução
O gráfico parece ter interceptações x em\(x=–2\)\(x=3\) e. Em ambos, o gráfico passa pelo intercepto, sugerindo fatores lineares. O gráfico tem duas assíntotas verticais. Aquele em\(x=–1\) parece exibir um comportamento básico semelhante ao\(\dfrac{1}{x}\), com o gráfico indo em direção ao infinito positivo de um lado e indo em direção ao infinito negativo do outro. A assíntota at\(x=2\) está exibindo um comportamento semelhante a\(\dfrac{1}{x^2}\), com o gráfico indo em direção ao infinito negativo em ambos os lados da assíntota. Veja a Figura\(\PageIndex{25}\).
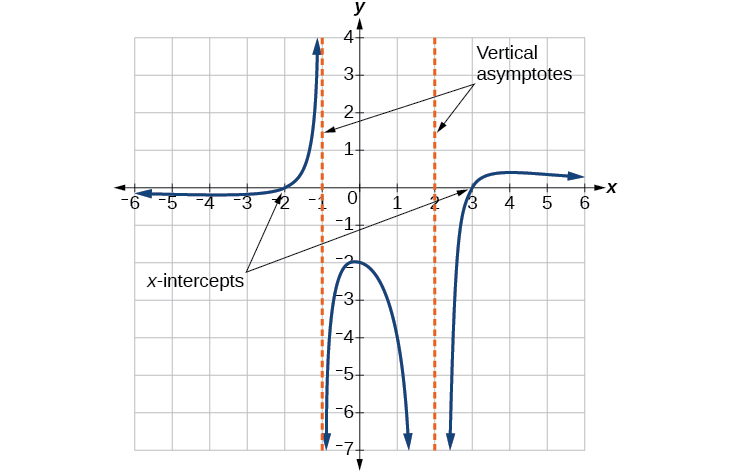
Podemos usar essas informações para escrever uma função do formulário
Para encontrar o fator de estiramento, podemos usar outro ponto claro no gráfico, como o intercepto \((0,–2)\)y.
Isso nos dá uma função final de\(f(x)=\dfrac{4(x+2)(x−3)}{3(x+1){(x−2)}^2}\).
Mídia
Acesse esses recursos on-line para obter instruções e práticas adicionais com funções racionais.
Equações chave
Função racional\( \qquad \)\(f(x)=\dfrac{P(x)}{Q(x)}=\dfrac{a_px^p+a_{p−1}x^{p−1}+...+a_1x+a_0}{b_qx^q+b_{q−1}x^{q−1}+...+b_1x+b_0},\space Q(x)≠0\)
Conceitos chave
- Podemos usar a notação de seta para descrever o comportamento local e o comportamento final das funções do kit de ferramentas\(f(x)=\frac{1}{x}\)\(f(x)=\frac{1}{x^2}\) e. Veja o exemplo\(\PageIndex{1}\).
- Uma função que se nivela em um valor horizontal tem uma assíntota horizontal. Uma função pode ter mais de uma assíntota vertical. Veja o exemplo.
- Problemas de aplicação envolvendo taxas e concentrações geralmente envolvem funções racionais. Veja o exemplo.
- O domínio de uma função racional inclui todos os números reais, exceto aqueles que fazem com que o denominador seja igual a zero. Veja o exemplo.
- As assíntotas verticais de uma função racional ocorrerão onde o denominador da função é igual a zero e o numerador não é zero. Veja o exemplo.
- Uma descontinuidade removível pode ocorrer no gráfico de uma função racional se uma entrada fizer com que o numerador e o denominador sejam zero. Veja o exemplo.
- O comportamento final de uma função racional refletirá o da razão dos termos principais das funções numerador e denominador. Veja exemplo, exemplo, exemplo e exemplo.
- Represente graficamente funções racionais encontrando as interceptações, o comportamento nas interceptações e assíntotas e o comportamento final. Veja o exemplo.
- Se uma função racional tem interceptos x em\(x=x_1,x_2,…,x_n\), assíntotas verticais em\(x=v_1,v_2,…,v_m\) e\(x_i=\) nenhuma\(v_j\), então a função pode ser escrita na forma


