Skip to main content
Global

5.3E: Gráficos de funções polinomiais (exercícios)

  1. Last updated
  2. Save as PDF
  • Page ID
    187115

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Para os exercícios a seguir, encontre todos os zeros da função polinomial, observando as multiplicidades.

    13. \(f(x)=(x+3)^{2}(2 x-1)(x+1)^{3}\)

    14. \(f(x)=x^{5}+4 x^{4}+4 x^{3}\)

    15. \(f(x)=x^{3}-4 x^{2}+x-4\)

    Para os exercícios a seguir, com base no gráfico fornecido, determine os zeros da função e observe a multiplicidade.

    16.

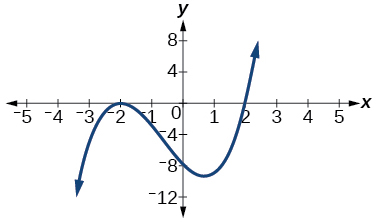
    Gráfico de um polinômio de grau ímpar com dois pontos de inflexão.

    17.

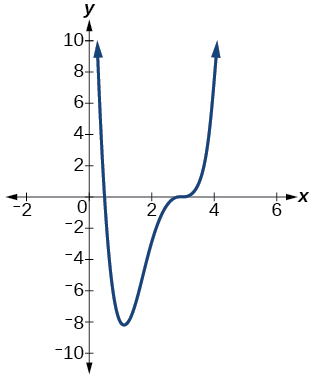
    Gráfico de um polinômio de grau par com dois pontos de inflexão.

    18.

    Use o Teorema do Valor Intermediário para mostrar que pelo menos um zero está entre 2 e 3 para a função\[f(x)=x^{3}-5 x+1 \nonumber\]