4.3E: Ajustando modelos lineares aos dados (exercícios)

Last updated
Save as PDF

Page ID: 186595

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

34.

Desenhe um gráfico de dispersão para os dados na Tabela 2. Em seguida, determine se os dados parecem estar relacionados linearmente.

Tabela 2
0	-105
2	-50
4	1
6	55
8	105
10	160

35.

Desenhe um gráfico de dispersão para os dados na Tabela 3. Se quiséssemos saber quando a população chegaria a 15.000, a resposta envolveria interpolação ou extrapolação?

Tabela 3
Ano	População
1990	5.600
1995	5.950
2000	6.300
2005	6.600
2010	6.900

36.

Oito alunos foram convidados a estimar sua pontuação em um questionário de 10 pontos. Suas pontuações estimadas e reais são dadas na Tabela 4. Faça um gráfico dos pontos e, em seguida, desenhe uma linha que se ajuste aos dados.

Tabela 4
Previsto	Real
6	6
7	7
7	8
8	8
7	9
9	10
10	10
10	9

37. Desenhe uma linha de melhor ajuste para os dados plotados.

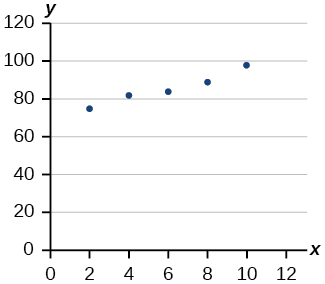
$Gráfico de dispersão dos pontos: (2,78); (4,81); (6,85); (8,90); e (10,99).$

Para os exercícios a seguir, considere os dados da Tabela 5, que mostra a porcentagem de desempregados em uma cidade de pessoas com 25 anos ou mais que são graduados universitários, é apresentada abaixo, por ano.

Tabela 5
Ano	2000	2002	2005	2007	2010
Percentual de graduados	6.5	7.0	7.4	8.2	9.0

38.

Determine se a tendência parece ser linear. Se sim, e supondo que a tendência continue, encontre um modelo de regressão linear para prever a porcentagem de desempregados em um determinado ano com três casas decimais.

39.

Em que ano o percentual ultrapassará 12%?

40.

Com base no conjunto de dados fornecido na Tabela 6, calcule a linha de regressão usando uma calculadora ou outra ferramenta tecnológica e determine o coeficiente de correlação com três casas decimais.

Tabela 6
xx	17	20	23	26	29
yy	15	25	31	37	40

Com base no conjunto de dados fornecido na Tabela 7, calcule a linha de regressão usando uma calculadora ou outra ferramenta tecnológica e determine o coeficiente de correlação com três casas decimais.

Tabela 7
xx	10	12	15	18	20
yy	36	34	30	28	22

Para os exercícios a seguir, considere este cenário: A população de uma cidade aumentou constantemente ao longo de um período de dez anos. Os seguintes pares ordenados mostram a população e o ano ao longo do período de dez anos (população, ano) para anos registrados específicos:

\[(3,600,2000) ;(4,000,2001) ;(4,700,2003) ;(6,000,2006)\]

42. Use a regressão linear para determinar uma função$y,$ em que o ano depende da população, com três casas decimais de precisão.

43. Preveja quando a população atingirá 12.000.

44. Qual é o coeficiente de correlação desse modelo com três casas decimais de precisão?

45. De acordo com o modelo, qual é a população em$2014 ?$