1.1: Números reais - Fundamentos da álgebra
- Page ID
- 186847
- Classifique um número real como um número natural, inteiro, inteiro, racional ou irracional.
- Execute cálculos usando a ordem das operações.
- Use as seguintes propriedades dos números reais: comutativo, associativo, distributivo, inverso e identidade.
- Avalie expressões algébricas.
- Simplifique as expressões algébricas.
Costuma-se dizer que a matemática é a linguagem da ciência. Se isso for verdade, a linguagem da matemática são os números. O primeiro uso de números ocorreu há\(100\) séculos no Oriente Médio para contar ou enumerar itens. Agricultores, pecuaristas e comerciantes usavam fichas, pedras ou marcadores para indicar uma única quantidade — um feixe de grãos, uma cabeça de gado ou um pedaço fixo de tecido, por exemplo. Isso tornou o comércio possível, levando à melhoria das comunicações e à disseminação da civilização.
Três a quatro mil anos atrás, os egípcios introduziram frações. Eles os usaram pela primeira vez para mostrar recíprocos. Posteriormente, eles os usaram para representar a quantidade quando uma quantidade foi dividida em partes iguais.
Mas e se não houvesse gado para comercializar ou se uma safra inteira de grãos fosse perdida em uma inundação? Como alguém poderia indicar a existência de nada? Desde os primeiros tempos, as pessoas pensaram em um “estado base” enquanto contavam e usavam vários símbolos para representar essa condição nula. No entanto, foi somente por volta do século V d.C. na Índia que o zero foi adicionado ao sistema numérico e usado como numeral nos cálculos.
Claramente, também havia a necessidade de números que representassem perdas ou dívidas. Na Índia, no século VII d.C., números negativos foram usados como soluções para equações matemáticas e dívidas comerciais. Os opostos dos números de contagem expandiram ainda mais o sistema numérico.
Devido à evolução do sistema numérico, agora podemos realizar cálculos complexos usando essas e outras categorias de números reais. Nesta seção, exploraremos conjuntos de números, cálculos com diferentes tipos de números e o uso de números em expressões.
Classificando um número real
Os números que usamos para contar ou enumerar itens são os números naturais,\(1, 2, 3, 4, 5\) e assim por diante. Nós os descrevemos em notação definida como\(\{1,2,3,...\}\) quando as reticências\((\cdots)\) indicam que os números continuam até o infinito. Os números naturais são, obviamente, também chamados de números de contagem. Sempre que enumeramos os membros de uma equipe, contamos as moedas de uma coleção ou contamos as árvores em um bosque, estamos usando o conjunto de números naturais. O conjunto de números inteiros é o conjunto de números naturais mais zero:\(\{0,1,2,3,...\}\).
O conjunto de números inteiros soma os opostos dos números naturais ao conjunto de números inteiros:\(\{\cdots,-3,-2,-1,0,1,2,3,\cdots\}\). É útil observar que o conjunto de números inteiros é composto por três subconjuntos distintos: números inteiros negativos, zero e números inteiros positivos. Nesse sentido, os números inteiros positivos são apenas os números naturais. Outra forma de pensar sobre isso é que os números naturais são um subconjunto dos números inteiros.
\[ \overbrace{\cdots, -3,-2,-1}^{\text{negative integers}}, \underbrace{0}_{\text{zero}}, \overbrace{1,\, 2,\,3,\, \cdots}^{\text{positive integers}} \nonumber\]
O conjunto de números racionais é escrito como\(\{\frac{m}{n}| \text{m and n are integers and } n \neq 0\}\) .Observe na definição que números racionais são frações (ou quocientes) contendo números inteiros no numerador e no denominador, e o denominador nunca é\(0\). Também podemos ver que todo número natural, número inteiro e inteiro é um número racional com um denominador de\(1\).
Por serem frações, qualquer número racional também pode ser expresso na forma decimal. Qualquer número racional pode ser representado como:
- um decimal final:\(\frac{15}{8} =1.875\), ou
- um decimal repetido:\(\frac{4}{11} =0.36363636\cdots = 0.\bar{36}\)
Usamos uma linha traçada sobre o bloco repetido de números em vez de escrever o grupo várias vezes.
Escreva cada um dos itens a seguir como um número racional. Escreva uma fração com o número inteiro no numerador e\(1\) in the denominator.
- \(7\)
- \(0\)
- \(-8\)
Solução
uma.\(7= \frac{7}{1}\)
b.\(0= \frac{0}{1}\)
c.\(-8= \frac{-8}{1}\)
Escreva cada um dos itens a seguir como um número racional.
- \(11\)
- \(3\)
- \(-4\)
- Resposta
-
- \(\frac{11}{1}\)
- \(\frac{3}{1}\)
- \(-\frac{4}{1}\)
Escreva cada um dos seguintes números racionais como decimal final ou repetitivo.
- \(-\frac{5}{7}\)
- \(\frac{15}{5}\)
- \(\frac{13}{25}\)
Solução
a. um decimal repetido
b.\(\frac{15}{5} = 3\) (ou\(3.0\)), um decimal de terminação
c.\(\frac{13}{25} =0.52\), um decimal final
Escreva cada um dos seguintes números racionais como decimal final ou repetitivo.
- \(\frac{68}{17}\)
- \(\frac{8}{13}\)
- \(-\frac{13}{25}\)
- Resposta
-
- \(4\)(ou\(4.0\)), encerrando
- \(0.\overline{615384}\), repetindo
- \(-0.85\), terminando
Números irracionais
Em algum momento do passado antigo, alguém descobriu que nem todos os números são números racionais. Um construtor, por exemplo, pode ter descoberto que a diagonal de um quadrado com lados unitários não era\(2\) ou uniforme\(32\), mas era outra coisa. Ou um fabricante de roupas pode ter observado que a proporção entre a circunferência e o diâmetro de um rolo de tecido era um pouco maior do que\(3\), mas ainda não era um número racional. Diz-se que esses números são irracionais porque não podem ser escritos como frações. Esses números compõem o conjunto de números irracionais. Números irracionais não podem ser expressos como uma fração de dois números inteiros. É impossível descrever esse conjunto de números por uma única regra, exceto para dizer que um número é irracional se não for racional. Então, escrevemos isso conforme mostrado.
\[\{h\mid h \text { is not a rational number}\}\]
Determine se cada um dos números a seguir é racional ou irracional. Se for racional, determine se é um decimal de terminação ou repetição.
- \(\sqrt{25}\)
- \(\frac{33}{9}\)
- \(\sqrt{11}\)
- \(\frac{17}{34}\)
- \(0.3033033303333…\)
Solução
- \(\sqrt{25}\): Isso pode ser simplificado como\(\sqrt{25} = 5\) .Portanto,\(\sqrt{25}\) é racional.
- \(\frac{33}{9}\): Porque é uma fração,\(\frac{33}{9}\) é um número racional. Em seguida, simplifique e divida. \[\frac{33}{9}=\cancel{\frac{33}{9}} \nonumber\]Então,\(\frac{33}{9}\) é racional e um decimal repetido.
- \(\sqrt{11}\): Isso não pode ser simplificado ainda mais. Portanto,\(\sqrt{11}\) é um número irracional.
- \(\frac{17}{34}\): Porque é uma fração,\(\frac{17}{34}\) é um número racional. Simplifique e divida. \[\frac{17}{34} = 0.5 \nonumber\]Então,\(\frac{17}{34}\) é racional e um decimal final.
- \(0.3033033303333…\)não é um decimal final. Observe também que não há um padrão de repetição porque o grupo de\(3s\) aumenta a cada vez. Portanto, não é um decimal final nem repetitivo e, portanto, não é um número racional. É um número irracional.
Determine se cada um dos números a seguir é racional ou irracional. Se for racional, determine se é um decimal de terminação ou repetição.
- \(\frac{7}{77}\)
- \(\sqrt{81}\)
- \(4.27027002700027…\)
- \(\frac{91}{13}\)
- \(\sqrt{39}\)
- Resposta
-
- racional e repetitivo;
- racional e terminador;
- irracional;
- racional e terminador;
- irracional
Números reais
Dado qualquer número\(n\), sabemos que\(n\) é racional ou irracional. Não pode ser as duas coisas. Os conjuntos de números racionais e irracionais juntos formam o conjunto de números reais. Como vimos com números inteiros, os números reais podem ser divididos em três subconjuntos: números reais negativos, zero e números reais positivos. Cada subconjunto inclui frações, decimais e números irracionais de acordo com seu sinal algébrico (+ ou —). O zero não é considerado positivo nem negativo.
Os números reais podem ser visualizados em uma reta numérica horizontal com um ponto arbitrário escolhido como\(0\), com números negativos à esquerda\(0\) e números positivos à direita de\(0\). Uma distância unitária fixa é então usada para marcar cada número inteiro (ou outro valor básico) em cada lado do\(0\). Qualquer número real corresponde a uma posição única na linha numérica. O inverso também é verdadeiro: cada localização na linha numérica corresponde exatamente a um número real. Isso é conhecido como correspondência individual. Nós nos referimos a isso como a reta numérica real, conforme mostrado na Figura (\(\PageIndex{1}\).

Classifique cada número como positivo ou negativo e como racional ou irracional. O número está à esquerda ou à direita\(0\) na reta numérica?
- \(-\frac{10}{3}\)
- \(-\sqrt{5}\)
- \(-6π\)
- \(0.615384615384…\)
Solução
- \(-\frac{10}{3}\)é negativo e racional. Está à\(0\) esquerda da reta numérica.
- \(-\sqrt{5}\)é positivo e irracional. Está à direita de\(0\).
- \(-\sqrt{289} = -\sqrt{17^2} = -17\)é negativo e racional. Está à esquerda de\(0\).
- \(-6π\)é negativo e irracional. Está à esquerda de\(0\).
- \(0.615384615384…\)é um decimal repetido, então é racional e positivo. Está à direita de\(0\).
Classifique cada número como positivo ou negativo e como racional ou irracional. O número está à esquerda ou à direita\(0\) na reta numérica?
- \(\sqrt{73}\)
- \(-11.411411411…\)
- \(\frac{47}{19}\)
- \(-\frac{\sqrt{5}}{2}\)
- \(6.210735\)
- Resposta
-
- positivo, irracional
- certo, negativo, racional
- esquerda positiva, racional
- certo, negativo, irracional
- esquerda positiva, racional; direita
Conjuntos de números como subconjuntos
Começando com os números naturais, expandimos cada conjunto para formar um conjunto maior, o que significa que há uma relação de subconjunto entre os conjuntos de números que encontramos até agora. Essas relações se tornam mais óbvias quando vistas como um diagrama, como Figura (\(\PageIndex{2}\)).
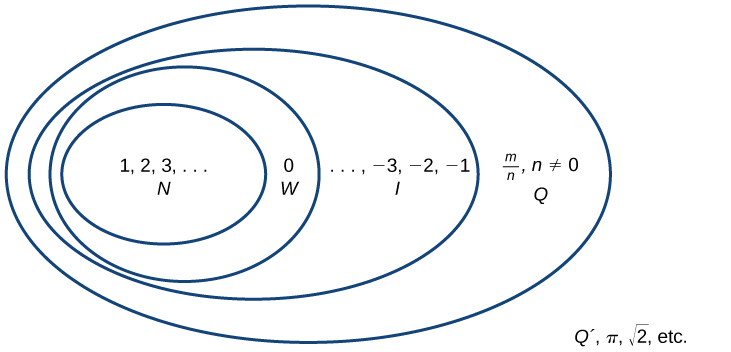
O conjunto de números naturais inclui os números usados para contar:\(\{1,2,3,...\}\).
O conjunto de números inteiros é o conjunto de números naturais mais zero:\(\{0,1,2,3,...\}\).
O conjunto de números inteiros soma os números naturais negativos ao conjunto de números inteiros:\(\{...,-3,-2,-1,0,1,2,3,...\}\).
O conjunto de números racionais inclui frações escritas como\(\{\frac{m}{n} | \text{m and n are integers and } n \neq 0\}\).
O conjunto de números irracionais é o conjunto de números que não são racionais, não se repetem e não terminam:\(\{h\parallel \text{h is not a rational number}\}\).
Classifique cada número como sendo um número natural (N), número inteiro (W), inteiro (I), número racional (Q) e/ou número irracional (Q).
- \(\sqrt{36}\)
- \(\frac{8}{3}\)
- \(\sqrt{73}\)
- \(-6\)
- \(3.2121121112…\)
Solução
| N | W | EU | Q | Q' | |
|---|---|---|---|---|---|
| uma.\(\sqrt{36} = 6\) | X | X | X | X | |
| b.\(\frac{8}{3} =2.\overline{6}\) | X | ||||
| c.\(\sqrt{73}\) | X | ||||
| d.\(-6\) | X | X | |||
| e.\(3.2121121112...\) | X |
Classifique cada número como sendo um número natural (N), número inteiro (W), inteiro (I), número racional (Q) e/ou número irracional (Q).
- \(-\frac{35}{7}\)
- \(0\)
- \(\sqrt{169}\)
- \(\sqrt{24}\)
- \(4.763763763...\)
- Resposta
-
N W EU Q Q' uma.\(-\frac{35}{7}\) X X b.\(0\) X X X c.\(\sqrt{169}\) X X X X d.\(\sqrt{24}\) X e.\(4.763763763...\) X
Executando cálculos usando a ordem das operações
Quando multiplicamos um número por si só, nós o elevamos ao quadrado ou o elevamos à potência de\(2\). Por exemplo,\(4^2 =4\times4=16\). Podemos elevar qualquer número a qualquer potência. Em geral, a notação exponencial an significa que o número ou a variável\(a\) é usado como um fator\(n\) vezes.
\[a^n=a\cdot a\cdot a\cdots a \qquad \text{ n factors} \nonumber \]
Nesta notação,\(a^n\) é lida como a\(n^{th}\) potência de\(a\), onde\(a\) é chamada de base e\(n\) é chamada de expoente. Um termo em notação exponencial pode fazer parte de uma expressão matemática, que é uma combinação de números e operações. Por exemplo,\(24+6 \times \dfrac{2}{3} − 4^2\) é uma expressão matemática.
Para avaliar uma expressão matemática, realizamos as várias operações. No entanto, não os executamos em nenhuma ordem aleatória. Usamos a ordem das operações. Essa é uma sequência de regras para avaliar essas expressões.
Lembre-se de que, em matemática, usamos parênteses (), colchetes [] e colchetes {} para agrupar números e expressões para que qualquer coisa que apareça dentro dos símbolos seja tratada como uma unidade. Além disso, barras fracionárias, radicais e barras de valor absoluto são tratadas como símbolos de agrupamento. Ao avaliar uma expressão matemática, comece simplificando as expressões dentro dos símbolos de agrupamento.
A próxima etapa é abordar quaisquer expoentes ou radicais. Depois, realize a multiplicação e a divisão da esquerda para a direita e, finalmente, a adição e subtração da esquerda para a direita.
Vamos dar uma olhada na expressão fornecida.
\[24+6 \times \dfrac{2}{3} − 4^2 \nonumber\]
Não há símbolos de agrupamento, então passamos para expoentes ou radicais. O número\(4\) é aumentado para uma potência de\(2\), então simplifique\(4^2\) quanto\(16\).
\[24+6 \times \dfrac{2}{3} − 4^2 \nonumber \]
\[24+6 \times \dfrac{2}{3} − 16 \nonumber\]
Em seguida, execute a multiplicação ou divisão, da esquerda para a direita.
\[24+6 \times \dfrac{2}{3} − 16 \nonumber\]
\[24+4-16 \nonumber\]
Por fim, faça adição ou subtração, da esquerda para a direita.
\[24+4−16 \nonumber\]
\[28−16 \nonumber\]
\[12 \nonumber\]
Portanto,
\[24+6 \times \dfrac{2}{3} − 4^2 =12 \nonumber\]
Para algumas expressões complicadas, várias passagens pela ordem das operações serão necessárias. Por exemplo, pode haver uma expressão radical entre parênteses que deve ser simplificada antes que os parênteses sejam avaliados. Seguir a ordem das operações garante que qualquer pessoa que simplifique a mesma expressão matemática obtenha o mesmo resultado.
As operações em expressões matemáticas devem ser avaliadas em uma ordem sistemática, que pode ser simplificada usando a sigla PEMDAS:
- P (próteses)
- (Expoentes)
- (Multiplicação) e D (Divisão)
- (Adição) e (Subtração)
- Simplifique qualquer expressão em símbolos de agrupamento.
- Simplifique qualquer expressão que contenha expoentes ou radicais.
- Execute qualquer multiplicação e divisão em ordem, da esquerda para a direita.
- Execute qualquer adição e subtração em ordem, da esquerda para a direita.
Use a ordem das operações para avaliar cada uma das expressões a seguir.
- \(\dfrac{5^2-4}{7}- \sqrt{11-2}\)
- \(\dfrac{14-3 \times2}{2 \times5-3^2}\)
- \(7\times(5\times3)−2\times[(6−3)−4^2]+1\)
Solução
- \[\begin{align*} (3\times2)^2-4\times(6+2)&=(6)^2-4\times(8) && \qquad \text{Simplify parentheses}\\ &=36-4\times8 && \qquad \text{Simplify exponent}\\ &=36-32 && \qquad \text{Simplify multiplication}\\ &=4 && \qquad \text{Simplify subtraction}\\ \end{align*}\]
- \[\begin{align*} \dfrac{5^2-4}{7}- \sqrt{11-2}&= \dfrac{5^2-4}{7}-\sqrt{9} && \qquad \text{Simplify grouping symbols (radical)}\\ &=\dfrac{5^2-4}{7}-3 && \qquad \text{Simplify radical}\\ &=\dfrac{25-4}{7}-3 && \qquad \text{Simplify exponent}\\ &=\dfrac{21}{7}-3 && \qquad \text{Simplify subtraction in numerator}\\ &=3-3 && \qquad \text{Simplify division}\\ &=0 && \qquad \text{Simplify subtraction} \end{align*}\]
Observe que na primeira etapa, o radical é tratado como um símbolo de agrupamento, como parênteses. Além disso, na terceira etapa, a barra fracionária é considerada um símbolo de agrupamento, então o numerador é considerado agrupado.
- \[\begin{align*} 6-\mid 5-8\mid +3\times(4-1)&=6-|-3|+3\times3 && \qquad \text{Simplify inside grouping symbols}\\ &=6-3+3\times3 && \qquad \text{Simplify absolute value}\\ &=6-3+9 && \qquad \text{Simplify multiplication}\\ &=3+9 && \qquad \text{Simplify subtraction}\\ &=12 && \qquad \text{Simplify addition}\\ \end{align*}\]
- \[\begin{align*} \dfrac{14-3 \times2}{2 \times5-3^2}&=\dfrac{14-3 \times2}{2 \times5-9} && \qquad \text{Simplify exponent}\\ &=\dfrac{14-6}{10-9} && \qquad \text{Simplify products}\\ &=\dfrac{8}{1} && \qquad \text{Simplify differences}\\ &=8 && \qquad \text{Simplify quotient}\\ \end{align*}\]
Neste exemplo, a barra de fração separa o numerador e o denominador, o que simplificamos separadamente até a última etapa.
- \[\begin{align*} 7\times(5\times3)-2\times[(6-3)-4^2]+1&=7\times(15)-2\times[(3)-4^2]+1 && \qquad \text{Simplify inside parentheses}\\ &=7\times(15)-2\times(3-16)+1 && \qquad \text{Simplify exponent}\\ &=7\times(15)-2\times(-13)+1 && \qquad \text{Subtract}\\ &=105+26+1 && \qquad \text{Multiply}\\ &=132 && \qquad \text{Add} \end{align*}\]
Use a ordem das operações para avaliar cada uma das expressões a seguir.
- \(\sqrt{5^2-4^2}+7\times(5-4)^2\)
- \(1+\dfrac{7\times5-8\times4}{9-6}\)
- \(|1.8-4.3|+0.4\times\sqrt{15+10}\)
- \(\dfrac{1}{2}\times[5\times3^2-7^2]+\dfrac{1}{3}\times9^2\)
- \([(3-8^2)-4]-(3-8)\)
- Resposta
-
- \(10\)
- \(2\)
- \(4.5\)
- \(25\)
- \(26\)
Usando propriedades de números reais
Para algumas atividades que realizamos, a ordem de determinadas operações não importa, mas a ordem de outras operações sim. Por exemplo, não faz diferença se calçarmos o sapato direito antes do esquerdo ou vice-versa. No entanto, importa se calçamos sapatos ou meias primeiro. O mesmo vale para operações em matemática.
Propriedades comutativas
A propriedade comutativa da adição afirma que os números podem ser adicionados em qualquer ordem sem afetar a soma.
\[a+b=b+a\]
Podemos ver melhor essa relação ao usar números reais.
\((−2)+7 = 5 \text{ and } 7+(−2)=5\)
Da mesma forma, a propriedade comutativa da multiplicação afirma que os números podem ser multiplicados em qualquer ordem sem afetar o produto.
\[a\times b=b\times a\]
Novamente, considere um exemplo com números reais.
É importante observar que nem a subtração nem a divisão são comutativas. Por exemplo, não\(17−5\) é o mesmo que\(5−17\). Da mesma forma,\(20÷5≠5÷20\).
Propriedades associativas
A propriedade associativa da multiplicação nos diz que não importa como agrupamos números ao multiplicar. Podemos mover os símbolos de agrupamento para facilitar o cálculo, e o produto permanece o mesmo.
\[a(bc)=(ab)c\]
Considere este exemplo.
\((3\times4)\times5=60 \text{ and } 3\times(4\times5)=60\)
A propriedade associativa da adição nos diz que os números podem ser agrupados de forma diferente sem afetar a soma.
\[a+(b+c)=(a+b)+c\]
Essa propriedade pode ser especialmente útil ao lidar com números inteiros negativos. Considere este exemplo.
\([15+(−9)]+23=29 \text{ and } 15+[(−9)+23]=29\)
A subtração e a divisão são associativas? Analise esses exemplos.
\[\begin{align*} 8-(3-15)\overset{?}{=}&(8-3)-15\\ 8-(-12)\overset{?}{=}&5-15\\ 20 \neq &10\\ 64\div (8\div 4)\overset{?}{=}&(64\div 8)\div 4\\ 64\div 2\overset{?}{=}&8\div 4\\ 32 \neq & 2 \end{align*}\]
Como podemos ver, nem a subtração nem a divisão são associativas.
Propriedade distributiva
A propriedade distributiva afirma que o produto de um fator vezes uma soma é a soma do fator vezes cada termo na soma.
\[a\times(b+c)=a\times b+a\times c\]
Essa propriedade combina adição e multiplicação (e é a única propriedade a fazer isso). Vamos considerar um exemplo.
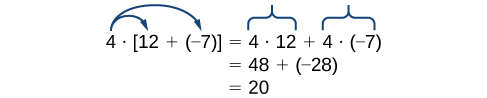
Note que\(4\) is outside the grouping symbols, so we distribute the \(4\) by multiplying it by \(12\), multiplying it by \(–7\), and adding the products.
To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.
\[\begin{align*} 6+(3\times5)\overset{?}{=}&(6+3)\times(6\times5)\\ 6+(15)\overset{?}{=}&(9)\times(11)\\ 21 \neq &99 \end{align*}\]
Multiplication does not distribute over subtraction, and division distributes over neither addition nor subtraction.
A special case of the distributive property occurs when a sum of terms is subtracted.
\[a−b=a+(−b)\]
For example, consider the difference \(12−(5+3)\). We can rewrite the difference of the two terms \(12\) and \((5+3)\) by turning the subtraction expression into addition of the opposite. So instead of subtracting \( (5+3)\), we add the opposite.
Now, distribute \(-1\) and simplify the result.
\[\begin{align*} 12-(5+3)&=12+(-1)\times(5+3)\\ &=12+[(-1)\times5+(-1)\times3]\\ &=12+(-8)\\ &=4 \end{align*}\]
This seems like a lot of trouble for a simple sum, but it illustrates a powerful result that will be useful once we introduce algebraic terms. To subtract a sum of terms, change the sign of each term and add the results. With this in mind, we can rewrite the last example.
\[\begin{align*} 12-(5+3)&=12+(-5-3)\\ &=12-8\\ &=4 \end{align*}\]
Identity Properties
The identity property of addition states that there is a unique number, called the additive identity \((0)\) that, when added to a number, results in the original number.
\[a+0=a\]
The identity property of multiplication states that there is a unique number, called the multiplicative identity \((1)\) that, when multiplied by a number, results in the original number.
\[a\times 1=a\]
For example, we have \( (−6)+0=−6\) and\( 23\times1=23\). There are no exceptions for these properties; they work for every real number, including \(0\) and \(1\).
Inverse Properties
The inverse property of addition states that, for every real number a, there is a unique number, called the additive inverse (or opposite), denoted \(−a\), that, when added to the original number, results in the additive identity, \(0\).
\[a+(−a)=0\]
For example, if \(a =−8\), the additive inverse is \(8\), since \((−8)+8=0\).
The inverse property of multiplication holds for all real numbers except \(0\) because the reciprocal of \(0\) is not defined. The property states that, for every real number \(a\), there is a unique number, called the multiplicative inverse (or reciprocal), denoted \(1a\), that, when multiplied by the original number, results in the multiplicative identity, \(1\).
\[a\times \dfrac{1}{a}=1\]
For example, if \(a =−\dfrac{2}{3}\), the reciprocal, denoted \(\dfrac{1}{a}\), is \(-\dfrac{3}{2}\) because
\[a⋅\dfrac{1}{a}=\left(−\dfrac{2}{3}\right)\times\left(−\dfrac{3}{2}\right)=1 \nonumber\]
The following properties hold for real numbers \(a\), \(b\), and \(c\).
| Addition | Multiplication | |
|---|---|---|
| Commutative Property | \(a+b=b+a\) | \(a\times b=b\times a\) |
| Associative Property | \(a+(b+c)=(a+b)+c\) | \(a(bc)=(ab)c\) |
| Distributive Property | \(a\times (b+c)=a\times b+a\times c\) | |
| Identity Property |
There exists a unique real number called the additive identity, 0, such that, for any real number a \(a+0=a\)
|
There exists a unique real number called the multiplicative identity, 1, such that, for any real number a \(a\times 1=a\)
|
| Inverse Property |
Every real number a has an additive inverse, or opposite, denoted –a, such that \(a+(−a)=0\)
|
Every nonzero real number a has a multiplicative inverse, or reciprocal, denoted 1a , such that \(a\times \left(\dfrac{1}{a}\right)=1\)
|
Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.
- \(3\times 6+3\times 4\)
- \((5+8)+(−8)\)
- \(6−(15+9)\)
- \(\dfrac{4}{7}\times\left(\dfrac{2}{3}\times \dfrac{7}{4}\right)\)
- \(100\times[0.75+(−2.38)]\)
Solution
- \[\begin{align*} 3\times6+3\times4&=3\times(6+4)\qquad \text{Distributive property}\\ &=3\times10\qquad \text{Simplify}\\ &=30\qquad \text{Simplify}\\ \end{align*}\]
- \[\begin{align*} (5+8)+(-8)&=5+[8+(-8)]\qquad \text{Associative property of addition}\\ &=5+0\qquad \text{Inverse property of addition}\\ &=5\qquad \text{Identity property of addition}\\ \end{align*}\]
- \[\begin{align*} 6-(15+9)&=6+[(-15)+(-9)]\qquad \text{Distributive property}\\ &=6+(-24)\qquad \text{Simplify}\\ &=-18\qquad \text{Simplify}\\ \end{align*}\]
- \[\begin{align*} \dfrac{4}{7}\times\left(\dfrac{2}{3}\times\dfrac{7}{4}\right)&=\dfrac{4}{7}\times\left(\dfrac{7}{4}\times\dfrac{2}{3}\right)\qquad \text{Commutative property of multiplication}\\ &=\left(\dfrac{4}{7}\times\dfrac{7}{4}\right)\times\dfrac{2}{3}\qquad \text{Associative property of multiplication}\\ &=1\times\dfrac{2}{3}\qquad \text{Inverse property of multiplication}\\ &=\dfrac{2}{3}\qquad \text{Identity property of multiplication}\\ \end{align*}\]
- \[\begin{align*} 100\times[0.75+(-2.38)]&=100\times0.75+100\times(-2.38)\qquad \text{Distributive property}\\ &=75+(-238)\qquad \text{Simplify}\\ &=-163\qquad \text{Simplify} \end{align*}\]
Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.
- \(\left(-\dfrac{23}{5}\right)\times\left[11\times\left(-\dfrac{5}{23}\right)\right]\)
- \(5\times(6.2+0.4)\)
- \(18-(7-15)\)
- \(\dfrac{17}{18}+\left[\dfrac{4}{9}+\left(-\dfrac{17}{18}\right)\right]\)
- \(6\times(-3)+6\times3\)
- Answer
-
- \(11)\), commutative property of multiplication
- \(33\), distributive property
- \(26\), distributive property
- \(\dfrac{4}{9}\), commutative property of addition, associative property of addition, inverse property of addition, identity property of addition
- \(0\), distributive property, inverse property of addition, identity property of addition
Evaluating Algebraic Expressions
So far, the mathematical expressions we have seen have involved real numbers only. In mathematics, we may see expressions such as \(x +5\), \(\dfrac{4}{3}\pi r^3\), or \(\sqrt{2m^3 n^2}\). In the expression \(x +5\), \(5\) is called a constant because it does not vary and \(x\) is called a variable because it does. (In naming the variable, ignore any exponents or radicals containing the variable.) An algebraic expression is a collection of constants and variables joined together by the algebraic operations of addition, subtraction, multiplication, and division.
We have already seen some real number examples of exponential notation, a shorthand method of writing products of the same factor. When variables are used, the constants and variables are treated the same way.
\[\begin{align*} (-3)^5 &=(-3)\times(-3)\times(-3)\times(-3)\times(-3)\Rightarrow x^5=x\times x\times x\times x\times x\\ (2\times7)^3&=(2\times7)\times(2\times7)\times(2\times7)\qquad \; \; \Rightarrow (yz)^3=(yz)\times(yz)\times(yz) \end{align*}\]
In each case, the exponent tells us how many factors of the base to use, whether the base consists of constants or variables.
Any variable in an algebraic expression may take on or be assigned different values. When that happens, the value of the algebraic expression changes. To evaluate an algebraic expression means to determine the value of the expression for a given value of each variable in the expression. Replace each variable in the expression with the given value, then simplify the resulting expression using the order of operations. If the algebraic expression contains more than one variable, replace each variable with its assigned value and simplify the expression as before.
List the constants and variables for each algebraic expression.
- \(x + 5\)
- \(\dfrac{4}{3}\pi r^3\)
- \(\sqrt{2m^3 n^2}\)
Solution
| Constants | Variables | |
|---|---|---|
| a. \(x + 5\) | \(5\) | \(x\) |
| b. \(\dfrac{4}{3}\pi r^3\) | \(\dfrac{4}{3}\), \(\pi\) | \(r\) |
| c. \(\sqrt{2m^3 n^2}\) | \(2\) | \(m\),\(n\) |
List the constants and variables for each algebraic expression.
- \(2(L + W)\)
- \(4y^3+y\)
- Answer
-
Constants Variables a. \(2\pi r(r+h)\) \(2\),\(\pi\) \(r\),\(h\) b. \(2(L + W)\) \(2\) \(L\), \(W\) c. \(4y^3+y\) \(4\) \(y\)
Evaluate the expression \(2x−7\) for each value for \(x\).
- \(x=0\)
- \(x=1\)
- \(x=12\)
- \(x=−4\)
Solution
- Substitute \(0\) for \(x\). \[\begin{align*} 2x-7 &= 2(0)-7 \\ &= 0-7\\ &= -7\\ \end{align*}\]
- Substitute \(1\) for \(x\). \[\begin{align*} 2x-7 &= 2(1)-7 \\ &= 2-7\\ &= -5\\ \end{align*}\]
- Substitute \(\dfrac{1}{2}\) for \(x\). \[\begin{align*} 2x-7 &= 2\left (\dfrac{1}{2} \right )-7 \\ &= 1-7\\ &= -6\\ \end{align*}\]
- Substitute \(-4\) for \(x\). \[\begin{align*} 2x-7 &= 2(-4)-7 \\ &= -8-7\\ &= -15\\ \end{align*}\]
Evaluate the expression \(11−3y\) for each value for \(y\).
- \(y=2\)
- \(y=0\)
- \(y=\dfrac{2}{3}\)
- \(y=−5\)
- Answer
-
- \(11\)
- \(26\)
Evaluate each expression for the given values.
- \(x+5\) for \(x=-5\)
- \(\dfrac{t}{2t-1}\) for \(t=10\)
- \(\dfrac{4}{3}\pi r^3\) for \(r=5\)
- \(a+ab+b\) for \(a=11\), \(b=-8\)
- \(\sqrt{2m^3 n^2}\) for \(m=2\), \(n=3\)
Solution
- Substitute
\(-5\) for \(x\). \[\begin{align*} x+5 &= (-5)+5 \\ &= 0\\ \end{align*}\] - Substitute \(10\) for \(t\). \[\begin{align*} \dfrac{t}{2t-1} &= \dfrac{(10)}{2(10)-1} \\ &= \dfrac{10}{20-1}\\ &= \dfrac{10}{19}\\ \end{align*}\]
- Substitute \(5\) for \(r\)
. \[\begin{align*} \dfrac{4}{3} \pi r^3 &= \dfrac{4}{3}\pi (5)^3 \\ &= \dfrac{4}{3}\pi (125)\\ &= \dfrac{500}{3}\pi\\ \end{align*}\] - Substitute \(11\) for \(a\) and \(-8\) for \(b\)
. \[\begin{align*} a+ab+b &= (11)+(11)(-8)+(-8) \\ &= 11-88-8 \\ &= -85\\ \end{align*}\] - Substitute \(2\) for \(m\) and \(3\) for \(n\). \[\begin{align*} \sqrt{2m^3 n^2} &= \sqrt{2(2)^3 (3)^2} \\ &= \sqrt{2(8)(9)} \\ &= \sqrt{144} \\ &= 12 \end{align*}\]
Evaluate each expression for the given values.
- \(\dfrac{y+3}{y-3}\) for \(y=5\)
- \(7-2t\) for \(t=-2\)
- \(\dfrac{1}{3}\pi r^2\) for \(r=11\)
- \((p^2 q)^3\) for \(p=-2\), \(q=3\)
- \(4(m-n)-5(n-m)\) for \(m=\dfrac{2}{3}\) \(n=\dfrac{1}{3}\)
- Answer
-
- \(4\)
- \(11\)
- \(\dfrac{121}{3}\pi\)
- \(1728\)
- \(3\)
Formulas
An equation is a mathematical statement indicating that two expressions are equal. The expressions can be numerical or algebraic. The equation is not inherently true or false, but only a proposition. The values that make the equation true, the solutions, are found using the properties of real numbers and other results. For example, the equation \(2x +1= 7\) has the unique solution of \(3\) because when we substitute \(3\) for \(x\) in the equation, we obtain the true statement \(2(3)+1=7\).
A formula is an equation expressing a relationship between constant and variable quantities. Very often, the equation is a means of finding the value of one quantity (often a single variable) in terms of another or other quantities. One of the most common examples is the formula for finding the area \(A\) of a circle in terms of the radius \(r\) of the circle: \( A= \pi r^2\). For any value of \(r\), the area \(A\) can be found by evaluating the expression \(\pi r^2\).
A right circular cylinder with radius \(r\) and height \(h\) has the surface area \(S\) (in square units) given by the formula \(S=2\pi r(r+h)\). See Figure \(\PageIndex{3}\). Find the surface area of a cylinder with radius \(6\) in. and height \(9\) in. Leave the answer in terms of \(\pi\).
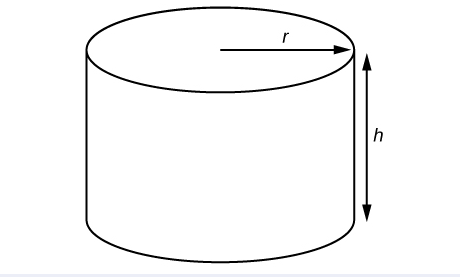
Evaluate the expression \(2\pi r(r+h)\) for \(r=6\) and \(h=9\).
Solution
\[\begin{align*} S &= 2\pi r(r+h) \\ &= 2\pi (6)[(6)+(9)] \\ &= 2\pi(6)(15) \\ &= 180\pi \end{align*}\]
The surface area is \(180\pi\) square inches.
A photograph with length \(L\) and width \(W\) is placed in a matte of width \(8\) centimeters (cm). The area of the matte (in square centimeters, or \(cm^2\) is found to be \(A=(L+16)(W+16) - L\)⋅W
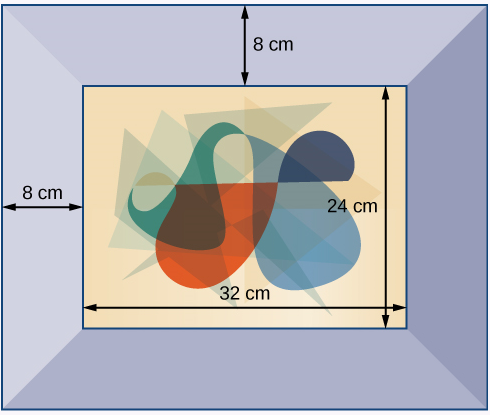
- Answer
-
\(1152cm^2\)
Simplifying Algebraic Expressions
Sometimes we can simplify an algebraic expression to make it easier to evaluate or to use in some other way. To do so, we use the properties of real numbers. We can use the same properties in formulas because they contain algebraic expressions.
Simplify each algebraic expression.
- \(3x-2y+x-3y-7\)
- \(2r-5(3-r)+4\)
- \(\left(4t-\dfrac{5}{4}s\right)-\left(\dfrac{2}{3}t+2s\right)\)
- \(2mn-5m+3mn+n\)
Solution
- \[\begin{align*} 3x-2y+x-3y-7&=3x+x-2y-3y-7 && \qquad \text{Commutative property of addition}\\ &=4x-5y-7 && \qquad \text{Simplify}\\ \end{align*}\]
- \[\begin{align*} 2r-5(3-r)+4&=2r-15+5r+4 && \qquad \qquad \qquad \text {Distributive property}\\ &=2r+5y-15+4 && \qquad \qquad \qquad \text{Commutative property of addition}\\ &=7r-11 && \qquad \qquad \qquad \text{Simplify}\\ \end{align*}\]
- \[\begin{align*} \left(4t-\dfrac{5}{4}s\right)-\left(\dfrac{2}{3}t+2s\right)&=4t-\dfrac{5}{4}s-\dfrac{2}{3}t-2s && \qquad \text{Distributive property}\\ &=4t-\dfrac{2}{3}t-\dfrac{5}{4}s-2s && \qquad \text{Commutative property of addition}\\ &=\dfrac{10}{3}t-\dfrac{13}{4}s && \qquad \text{Simplify}\\ \end{align*}\]
- \[\begin{align*} 2mn-5m+3mn+n&=2mn+3mn-5m+n && \qquad \text{Commutative property of addition}\\ &=5mn-5m+n && \qquad \text{Simplify}\\ \end{align*}\]
Simplify each algebraic expression.
- \(\dfrac{2}{3}y−2\left(\dfrac{4}{3}y+z\right)\)
- \(\dfrac{5}{t}−2−\dfrac{3}{t}+1\)
- \(4p(q−1)+q(1−p)\)
- \(9r−(s+2r)+(6−s)\)
- Answer
-
- \(−2y−2z\) or \(−2(y+z)\)
- \(\dfrac{2}{t}−1\)
- \(3pq−4p+q\)
- \(7r−2s+6\)
A rectangle with length \(L\) and width \(W\) has a perimeter \(P\) given by \(P =L+W+L+W\). Simplify this expression.
Solution
\[\begin{align*} P &=L+W+L+W\\ P &=L+L+W+W && \qquad \text{Commutative property of addition}\\ P &=2L+2W && \qquad \text{Simplify}\\ P &=2(L+W) && \qquad \text{Distributive property} \end{align*}\]
If the amount \(P\) is deposited into an account paying simple interest \(r\) for time \(t\), the total value of the deposit \(A\) is given by \(A =P+Prt\). Simplify the expression. (This formula will be explored in more detail later in the course.)
- Answer
-
\(A=P(1+rt)\)
Access these online resources for additional instruction and practice with real numbers.
Key Concepts
- Rational numbers may be written as fractions or terminating or repeating decimals. See Example and Example.
- Determine whether a number is rational or irrational by writing it as a decimal. See Example.
- The rational numbers and irrational numbers make up the set of real numbers. See Example. A number can be classified as natural, whole, integer, rational, or irrational. See Example.
- The order of operations is used to evaluate expressions. See Example.
- The real numbers under the operations of addition and multiplication obey basic rules, known as the properties of real numbers. These are the commutative properties, the associative properties, the distributive property, the identity properties, and the inverse properties. See Example.
- Algebraic expressions are composed of constants and variables that are combined using addition, subtraction, multiplication, and division. See Example. They take on a numerical value when evaluated by replacing variables with constants. See Example,Example, and Example
- Formulas are equations in which one quantity is represented in terms of other quantities. They may be simplified or evaluated as any mathematical expression. See Example and Example.
Glossary
- algebraic expression
- constants and variables combined using addition, subtraction, multiplication, and division
- associative property of addition
- the sum of three numbers may be grouped differently without affecting the result; in symbols,a+(b+c)=(a+b)+c
- associative property of multiplication
- the product of three numbers may be grouped differently without affecting the result; in symbols,a⋅(b⋅c)=(a⋅b)⋅c
- base
- in exponential notation, the expression that is being multiplied
- commutative property of addition
- two numbers may be added in either order without affecting the result; in symbols,a+b=b+a
- commutative property of multiplication
- two numbers may be multiplied in any order without affecting the result; in symbols,a⋅b=b⋅a
- constant
- a quantity that does not change value
- distributive property
- the product of a factor times a sum is the sum of the factor times each term in the sum; in symbols,a⋅(b+c)=a⋅b+a⋅c
- equation
- a mathematical statement indicating that two expressions are equal
- exponent
- in exponential notation, the raised number or variable that indicates how many times the base is being multiplied
- exponential notation
- a shorthand method of writing products of the same factor
- formula
- an equation expressing a relationship between constant and variable quantities
- identity property of addition
- there is a unique number, called the additive identity, 0, which, when added to a number, results in the original number; in symbols,a+0=a
- identity property of multiplication
- there is a unique number, called the multiplicative identity, 1, which, when multiplied by a number, results in the original number; in symbols,a⋅1=a
- integers
- the set consisting of the natural numbers, their opposites, and 0:{…,−3,−2,−1,0,1,2,3,…}
- inverse property of addition
- for every real numbera,there is a unique number, called the additive inverse (or opposite), denoted−a,which, when added to the original number, results in the additive identity, 0; in symbols,a+(−a)=0
- inverse property of multiplication
- for every non-zero real numbera,there is a unique number, called the multiplicative inverse (or reciprocal), denoted1a,which, when multiplied by the original number, results in the multiplicative identity, 1; in symbols,a⋅1a=1
- irrational numbers
- the set of all numbers that are not rational; they cannot be written as either a terminating or repeating decimal; they cannot be expressed as a fraction of two integers
- natural numbers
- the set of counting numbers:{1,2,3,…}
- order of operations
- a set of rules governing how mathematical expressions are to be evaluated, assigning priorities to operations
- rational numbers
- the set of all numbers of the formmn,wheremandnare integers andn≠0.Any rational number may be written as a fraction or a terminating or repeating decimal.
- real number line
- a horizontal line used to represent the real numbers. An arbitrary fixed point is chosen to represent 0; positive numbers lie to the right of 0 and negative numbers to the left.
- real numbers
- the sets of rational numbers and irrational numbers taken together
- variable
- a quantity that may change value
- whole numbers
- the set consisting of 0 plus the natural numbers:{0,1,2,3,…}


