18.10: Introdução à rotação de eixo fixo
- Page ID
- 184882
Verifique sua compreensão
10.1. a. 40,0 rev/s = 2\(pi\) (40,0) rad/s,\(\bar{\alpha} = \frac{\Delta \omega}{\Delta t} = \frac{2 \pi (40.0) − 0\; rad/s}{20.0\; s}\) = 2\(\pi\) (2,0) = 4,0\(\pi\) rad/s 2
b. Como a velocidade angular aumenta linearmente, deve haver uma aceleração constante ao longo do tempo indicado. Portanto, a aceleração angular instantânea a qualquer momento é a solução para 4,0\(\pi\) rad/s 2.
10.2. a. Usando a Equação 10.25, temos 7000 rpm =\(\frac{7000.0(2 \pi\; rad)}{60.0\; s}\) = 733,0 rad/s, $$\ alpha =\ frac {\ omega -\ omega_ {0}} {t} =\ frac {733.0\; rad/s} {10.0\; s} = 73.3\; rad/s^ {2}\]
b. Usando a Equação 10.29, temos $$\ omega^ {2} =\ omega_ {0} ^ {2} + 2\ alpha\ Delta\ theta\ Rightarrow\ Delta\ theta =\ frac {\ omega^ {2} -\ omega_ {0} ^ {2}} {2\ alpha} =\ frac {0 - (733.0\; rad/s) ^ {2}} {2 (73,3\; rad/s^ {2})} = 3665,2\; rad\]
10.3. A aceleração angular é\(\alpha = \frac{(5.0 − 0)\; rad/s}{20.0\; s}\) = 0,25 rad/s 2. Portanto, o ângulo total pelo qual o garoto passa é $$\ Delta\ theta =\ frac {\ omega^ {2} -\ omega_ {0} ^ {2}} {2\ alpha} =\ frac {(5.0) ^ {2} - 0} {2 (0,25)} = 50\; Rad$$Assim, calculamos $$s = r\ theta = (5,0\ m)) (50,0\; rad) = 250,0\; m\]
10.4. A energia cinética rotacional inicial da hélice é $$K_ {0} =\ frac {1} {2} I\ omega^ {2} =\ frac {1} {2} (800,0\; kg\ cdotp m^ {2}) (4,0\ times 2\ pi\; rad/s) ^ {2} = 2,53\ times 10^ {5}\; J\ LDOTP$$at 5,0 s a nova energia cinética rotacional da hélice é $$K_ {f} = 2,03\ times 10^ {5}\; J\ ldotp$$ e o a nova velocidade angular é $$\ omega =\ sqrt {\ frac {2 (2.03\ times 10^ {5}\; J)} {800.0\; kg\ cdotp m^ {2}}} = 22,53\; rad/s$$que é 3,58 rev/s.
10,5. I eixo paralelo = I centro de massa + md 2 = mR 2 + mR 2 = 2mR 2
10.6. O ângulo entre o braço da alavanca e o vetor de força é de 80°; portanto, r \(\perp\)= 100 m (sin 80°) = 98,5 m. O produto transversal\(\vec{\tau} = \vec{r} \times \vec{F}\) fornece um torque negativo ou no sentido horário. O torque é então\(\tau = - r_{\perp} F\) = −98,5 m (5,0 x 10 5 N) = −4,9 x 10 7 N • m.
10,7. a. A aceleração angular é\(\alpha = \frac{20.0(2 \pi)\; rad/s − 0}{10.0 \; s}\) = 12,56 rad/s 2. Resolvendo o torque, temos\(\sum_{i} \tau_{i} = I \alpha\) = (30,0 kg • m 2) (12,56 rad/s 2) = 376,80 N • m
b. A aceleração angular é\(\alpha = \frac{0 − 20.0(2 \pi)\; rad/s}{20.0\; s}\) = −6,28 rad/s 2. Resolvendo o torque, temos\(\sum_{i} \tau_{i} = I \alpha\) = (30,0 kg • m 2) (−6,28 rad/s 2) = −188,50 N • m
10,8. 3 MW
Perguntas conceituais
1. A segunda mão gira no sentido horário, então, pela regra da direita, o vetor de velocidade angular está na parede.
3. Eles têm a mesma velocidade angular. Os pontos mais distantes do bastão têm maiores velocidades tangenciais.
5. Linha reta, linear na variável de tempo
7. Constante
9. O vetor de aceleração centrípeta é perpendicular ao vetor de velocidade.
11. a. Ambos; b. aceleração centrípeta diferente de zero; c. ambos
13. A esfera oca, já que a massa é distribuída mais longe do eixo de rotação.
15. a. Diminui. b. Os braços podem ser aproximados com hastes e o disco com um disco. O torso está próximo ao eixo de rotação, então não contribui muito para o momento de inércia.
17. Porque o momento de inércia varia como o quadrado da distância até o eixo de rotação. A massa da haste localizada a distâncias maiores que L/2 forneceria a maior contribuição para tornar seu momento de inércia maior do que a massa pontual em\(\frac{L}{2}\).
19. Magnitude da força, comprimento do braço da alavanca e ângulo do braço da alavanca e vetor de força
21. O momento de inércia das rodas é reduzido, portanto, é necessário um torque menor para acelerá-las.
23. Sim
25. |\(\vec{r}\) | pode ser igual ao braço da alavanca, mas nunca menor que o braço da alavanca
27. Se as forças estiverem ao longo do eixo de rotação ou se tiverem o mesmo braço de alavanca e forem aplicadas em um ponto da haste.
Problemas
29. \(\omega = \frac{2 \pi\; rad}{45.0\; s}\)= 0,14 rad/s
31. a.\(\theta = \frac{s}{r} = \frac{3.0\; m}{1.5\; m}\) = 2,0 rad
b.\(\omega = \frac{2.0\; rad}{1.0\; s}\) = 2,0 rad/s
c.\(\frac{v^{2}}{r} = \frac{(3.0\; m/s)^{2}}{1.5\; m}\) = 6,0 m/s 2.
33. A hélice leva apenas\(\Delta\) t\(\frac{\Delta \omega}{\alpha} = \frac{0\; rad/s − 10.0(2 \pi)\; rad/s}{−2.0\; rad/s^{2}}\) = 31,4 s para descansar, quando a hélice está a 0 rad/s, ela começa a girar na direção oposta. Isso seria impossível devido à magnitude das forças envolvidas em fazer com que a hélice parasse e começasse a girar na direção oposta.
35. a.\(\omega\) = 25,0 (2,0 s) = 50,0 rad/s
b.\(\alpha = \frac{d \omega}{dt}\) = 25,0 rad/s 2
37. a.\(\omega\) = 54,8 rad/s
b. t = 11,0 s
39. a. 0,87 rad/s 2
b.\(\theta\) = 66.264 rad
41. a.\(\omega\) = 42,0 rad/s
b.\(\theta\) = 220 rad
c. v t = 42 m/s, a t = 4,0 m/s 2
43. a.\(\omega\) = 7,0 rad/s
b.\(\theta\) = 22,5 rad
c. a t = 0,1 m/s
45. \(\alpha\)= 28,6 rad/s 2.
47. r = 0,78 m
49. a.\(\alpha\) = −0,314 rad/s 2
b. a c = 197,4 m/s 2
c. a\(\sqrt{a_{c}^{2} + a_{t}^{2}} = \sqrt{197.4^{2} + (−6.28)^{2}}\) = 197,5 m/s 2,\(\theta\) = tan −1\(\frac{−6.28}{197.4}\) = −1,8° no sentido horário a partir do vetor de aceleração centrípeta
51. ma = 40,0 kg (5,1 m/s 2) = 204,0 N
A força máxima de atrito é\(\mu_{S}\) N = 0,6 (40,0 kg) (9,8 m/s 2) = 235,2 N para que a criança ainda não caia.
53. $$\ begin {split} v_ {t} & = r\ omega = 1,0 (2,0t)\; m/s\\ a_ {c} & =\ frac {v_ {t} ^ {2}} {r} =\ frac {(2,0t) ^ {2}} {1,0\; m} = 4,0t^ {2}\; m/s^ {2}\ a_ {t} (t) & = r\ alpha (t) = r\ frac {d\ omega} {dt} = 1,0\; m (2,0) = 2,0\; m/s^ {2}\ ldotp\ end {split} $$Traçar ambas as acelerações dá
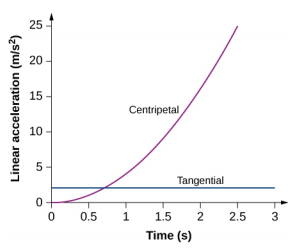
A aceleração tangencial é constante, enquanto a aceleração centrípeta depende do tempo e aumenta com o tempo para valores muito maiores do que a aceleração tangencial após t = 1s. Por vezes menores que 0,7 s e se aproximando de zero, a aceleração centrípeta é muito menor que a aceleração tangencial.
55. a. K = 2,56 x 10 29 J
b. K = 2,68 x 10 33 J
57. K = 434,0 J
59. a. v f = 86,5 m/s
b. A taxa de rotação da hélice permanece a mesma em 20 rotações/s.
61. K = 3,95 x 10 42 J
63. a. I = 0,315 kg • m 2
b. K = 621,8 J
65. I =\(\frac{7}{36}\) mL 2
67. v = 7,14 m/s.
69. \(\theta\)= 10,2°
71. F = 30 N
73. a. 0,85 m (55,0 N) = 46,75 N • m
b. Não importa em que altura você empurra.
75. m 2\(\frac{4.9\; N \cdotp m}{9.8(0.3\; m)}\) = 1,67 kg
77. \(\tau_{net}\)= −9,0 N • m + 3,46 N • m + 0 − 3,28 N • m = −8,82 N • m
79. \(\tau\)= 5,66 N • m
81. \(\sum \tau\)= 57,82 N • m
83. \(\vec{r} \times \vec{F}\)= 4,0\(\hat{i}\) + 2,0\(\hat{j}\) − 16,0\(\hat{k}\) N • m
85. a.\(\tau\) = (0,280 m) (180,0 N) = 50,4 N • m
b.\(\alpha\) = 17,14 rad/s 2
c.\(\alpha\) = 17,04 rad/s 2
87. \(\tau\)= 8,0 N • m
89. \(\tau\)= −43,6 N • m
91. a.\(\alpha\) = 1,4 x 10 −10 rad/s 2
b.\(\tau\) = 1,36 x 10 28 N • m
c. F = 2,1 x 10 21 N
93. a = 3,6 m/s 2
95. a. a = r\(\alpha\) = 14,7 m/s 2
b. a\(\frac{L}{2} \alpha\) =\(\frac{3}{4}\) g
97. \(\tau = \frac{P}{\omega} = \frac{2.0 \times 10^{6}\; W}{2.1\; rad/s}\)= 9,5 x 10 5 N • m
99. a. K = 888,50 J
b.\(\Delta \theta\) = 294,6 rev.
101. a. I = 114,6 kg • m 2
b. P = 104.700 W
103. v = L\(\omega\) =\(\sqrt{3Lg}\)
105. a. a = 5,0 m/s 2
b. W = 1,25 N • m
Problemas adicionais
107. \(\Delta\)t = 10,0 s
109. a. 0,06 rad/s 2
b.\(\theta\) = 105,0 rad
111. s = 405,26 m
113. a. I = 0,363 kg • m 2
b. I = 2,34 kg • m 2
115. \(\omega =\sqrt{\frac{5.36\; J}{4.4\; kg \cdotp m^{2}}}\)= 1,10 rad/s
117. F = 23,3 N
119. \(\alpha = \frac{190.0\; N \cdotp m}{2.94\; kg \cdotp m^{2}}\)= 64,4 rad/s 2
Problemas de desafio
121. a.\(\omega\) = 2,0 t − 1,5 t 2
b.\(\theta\) = t 2 − 0,5 t 3
c.\(\theta\) = −400,0 rad
d. o vetor está em −0,66 (360°) = −237,6°
123. I =\(\frac{2}{5}\) mR 2
125. a.\(\omega\) = 8,2 rad/s
b.\(\omega\) = 8,0 rad/s


