11.2: Movimento de rolamento

Last updated
Save as PDF

Page ID: 184782

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Descreva a física do movimento de rolamento sem escorregar
Explicar como as variáveis lineares estão relacionadas às variáveis angulares no caso de movimento de rolamento sem escorregamento
Encontre as acelerações lineares e angulares em movimento de rolamento com e sem escorregamento
Calcule a força de atrito estática associada ao movimento de rolamento sem escorregar
Use a conservação de energia para analisar o movimento de rolamento

O movimento de rolamento é aquela combinação comum de movimento rotacional e translacional que vemos em todos os lugares, todos os dias. Pense nas diferentes situações de rodas se movendo em um carro ao longo de uma rodovia, ou rodas em um avião pousando em uma pista ou rodas em um explorador robótico em outro planeta. Compreender as forças e torques envolvidos no movimento de rolamento é um fator crucial em muitos tipos diferentes de situações.

Para analisar o movimento de rolamento neste capítulo, consulte a Figura 10.5.4 em Rotação de eixo fixo para encontrar momentos de inércia de alguns objetos geométricos comuns. Você também pode achá-lo útil em outros cálculos que envolvem rotação.

Movimento de rolamento sem escorregar

As pessoas observaram o movimento de rolamento sem escorregar desde a invenção da roda. Por exemplo, podemos observar a interação dos pneus de um carro com a superfície da estrada. Se o motorista pressionar o acelerador no chão, de forma que os pneus girem sem que o carro avance, deve haver atrito cinético entre as rodas e a superfície da estrada. Se o motorista pressionar o acelerador lentamente, fazendo com que o carro avance, os pneus rolarão sem escorregar. É surpreendente para a maioria das pessoas que, de fato, a parte inferior da roda esteja em repouso em relação ao solo, indicando que deve haver atrito estático entre os pneus e a superfície da estrada. Na Figura$\PageIndex{1}$, a bicicleta está em movimento com o motociclista em pé. Os pneus entram em contato com a superfície da estrada e, mesmo rolando, a parte inferior dos pneus se deforma levemente, não escorregam e ficam em repouso em relação à superfície da estrada por um período mensurável de tempo. Para que isso aconteça, deve haver atrito estático entre o pneu e a superfície da estrada.

A Figura a é uma fotografia de uma pessoa andando de bicicleta. A câmera acompanhou a bicicleta, então a imagem da bicicleta e do ciclista é nítida, o fundo ficou desfocado devido ao movimento da bicicleta. A Figura b é uma fotografia de uma roda de bicicleta rolando no chão, com a câmera parada em relação ao solo. A roda e os raios estão borrados na parte superior, mas transparentes na parte inferior. — Figura$\PageIndex{1}$: (a) A bicicleta avança e seus pneus não escorregam. A parte inferior do pneu levemente deformado fica em repouso em relação à superfície da estrada por um período mensurável de tempo. (b) Esta imagem mostra que a parte superior de uma roda giratória parece embaçada por seu movimento, mas a parte inferior da roda fica instantaneamente em repouso. (crédito a: modificação da obra de Nelson Lourenço; crédito b: modificação da obra de Colin Rose)

Para analisar o rolamento sem escorregar, primeiro derivamos as variáveis lineares de velocidade e aceleração do centro de massa da roda em termos das variáveis angulares que descrevem o movimento da roda. A situação é mostrada na Figura$\PageIndex{2}$.

A Figura a mostra um diagrama de corpo livre de uma roda, incluindo o local onde as forças atuam. Quatro forças são mostradas: M g é uma força descendente que atua no centro da roda. N é uma força ascendente atuando na parte inferior da roda. F é uma força para a direita, atuando no centro da roda, e f sub s é uma força para a esquerda atuando na parte inferior da roda. A força f sub s é menor ou igual a mu sub s vezes N. A Figura b é uma ilustração de uma roda rolando sem escorregar em uma superfície horizontal. O ponto P é o ponto de contato entre a parte inferior da roda e a superfície. A roda tem uma rotação no sentido horário, uma aceleração à direita de um sub C M e uma velocidade à direita de v sub V M. As relações ômega é igual a v sub C M sobre R e alfa igual a sub C M sobre R são dadas. Um sistema de coordenadas com x positivo à direita e y positivo para cima é mostrado. A Figura c mostra a roda no centro da estrutura de massa. O ponto P tem vetor de velocidade na direção negativa em relação ao centro de massa da roda. Esse vetor é mostrado no diagrama e rotulado como menos R ômega i hat. É tangente à roda na parte inferior e aponta para a esquerda. Vetores adicionais em vários locais na borda da roda são mostrados, todos tangentes à roda e apontando no sentido horário. — Figura$\PageIndex{2}$: (a) Uma roda é puxada através de uma superfície horizontal por uma força$\vec{F}$. A força de atrito estático$\vec{f}_{s}$,$|\vec{f}_{s}|$ ≤$\mu_{s}$ N, é grande o suficiente para evitar que escorregue. (b) Os vetores lineares de velocidade e aceleração do centro de massa e as expressões relevantes para$\omega$$\alpha$ e. O ponto P está em repouso em relação à superfície. (c) Em relação à estrutura do centro de massa (CM), o ponto P tem velocidade linear −R$\omega \hat{i}$.

Na Figura$\PageIndex{2}$ (a), vemos os vetores de força envolvidos na prevenção do deslizamento da roda. Em (b), o ponto P que toca a superfície está em repouso em relação à superfície. Em relação ao centro de massa, o ponto P tem velocidade −R$\omega \hat{i}$, onde R é o raio da roda e$\omega$ é a velocidade angular da roda em torno de seu eixo. Como a roda está rolando, a velocidade de P em relação à superfície é sua velocidade em relação ao centro de massa mais a velocidade do centro de massa em relação à superfície:

\[\vec{v}_{P} = -R \omega \hat{i} + v_{CM} \hat{i} \ldotp\]

Como a velocidade de P em relação à superfície é zero, v _P = 0, isso diz que

\[v_{CM} = R \omega \ldotp \label{11.1}\]

Assim, a velocidade do centro de massa da roda é seu raio vezes a velocidade angular em torno de seu eixo. Mostramos a correspondência da variável linear no lado esquerdo da equação com a variável angular no lado direito da equação. Isso é feito abaixo para a aceleração linear.

Se diferenciarmos a Equação\ ref {11.1} no lado esquerdo da equação, obtemos uma expressão para a aceleração linear do centro de massa. No lado direito da equação, R é uma constante e$\alpha = \frac{d \omega}{dt}$, desde então, temos

\[a_{CM} = R \alpha \ldotp \label{11.2}\]

Além disso, podemos encontrar a distância que a roda percorre em termos de variáveis angulares consultando a Figura$\PageIndex{3}$. À medida que a roda rola do ponto A para o ponto B, sua superfície externa mapeia o solo exatamente pela distância percorrida, que é d _CM.

Vemos na Figura$\PageIndex{3}$ que o comprimento da superfície externa que mapeia o solo é o comprimento do arco$\theta$ R. Equacionando as duas distâncias, obtemos

\[d_{CM} = R \theta \ldotp \label{11.3}\]

Uma roda, raio R, rolando em uma superfície horizontal e se movendo para a direita em v sub C M é desenhada em duas posições. Na primeira posição, o ponto A na roda está na parte inferior, em contato com a superfície, e o ponto B está na parte superior. O comprimento do arco de A a B ao longo da borda da roda é destacado e rotulado como sendo R teta. Na segunda posição, o ponto B da roda está na parte inferior, em contato com a superfície, e o ponto A está na parte superior. A distância horizontal entre o ponto de contato da roda com a superfície nas duas posições ilustradas é d sub C M. O comprimento do arco A B agora está do outro lado da roda. — Figura$\PageIndex{3}$: À medida que a roda rola na superfície, o comprimento do arco R$\theta$ de A a B é mapeado na superfície, correspondendo à distância d _CM que o centro de massa se moveu.

Exemplo$\PageIndex{1}$: Rolling Down an Inclined Plane

Um cilindro sólido desce por um plano inclinado sem escorregar, começando do repouso. Tem massa m e raio r. (a) Qual é sua aceleração? (b) Em que condição o coeficiente de atrito estático deve$\mu_{S}$ satisfazer para que o cilindro não escorregue?

Estratégia

Desenhe um esboço e um diagrama de corpo livre e escolha um sistema de coordenadas. Colocamos x na direção abaixo do plano e y para cima perpendicularmente ao plano. Identifique as forças envolvidas. Essas são a força normal, a força da gravidade e a força devido ao atrito. Anote as leis de Newton nas direções x e y e a lei de Newton para rotação e resolva a aceleração e a força devidas ao atrito.

Solução

O diagrama de corpo livre e o esboço são mostrados na Figura$\PageIndex{4}$, incluindo a força normal, os componentes do peso e a força de atrito estática. Quase não há atrito suficiente para manter o cilindro rolando sem escorregar. Como não há deslizamento, a magnitude da força de atrito é menor ou igual a$\mu_{S}$ N. Escrevendo as leis de Newton nas direções x e y, temos

\[\sum F_{x} = ma_{x};\; \sum F_{y} = ma_{y} \ldotp\]

Um diagrama de um cilindro rolando sem deslizar por um plano inclinado e um diagrama de corpo livre do cilindro. À esquerda está uma ilustração mostrando o plano inclinado, que forma um ângulo de teta com a horizontal. Mostra-se que o cilindro está em repouso na parte superior e, em seguida, se movendo ao longo da inclinação quando está mais baixo. À direita está um diagrama corporal gratuito. O sistema de coordenadas x y é inclinado de forma que a direção x positiva seja paralela ao plano inclinado e aponte para sua parte inferior, e a direção y positiva seja para fora, perpendicular ao plano. Quatro forças são mostradas. N j hat atua no centro do cilindro e aponta na direção y positiva. m g sine theta i hat atua no centro do cilindro e aponta na direção x positiva. Menos m g cosseno theta j hat atua no centro do cilindro e aponta na direção y negativa. Menos f sub s i que atua no ponto de contato e aponta na direção negativa x. — Figura$\PageIndex{4}$: Um cilindro sólido desce por um plano inclinado sem escorregar do repouso. O sistema de coordenadas tem x na direção abaixo do plano inclinado e y perpendicular ao plano. O diagrama de corpo livre é mostrado com a força normal, a força de atrito estática e os componentes do peso$\vec{g}$ m. O atrito faz com que o cilindro role pelo avião em vez de escorregar.

Substituindo a partir do diagrama de corpo livre

\[\begin{split} mg \sin \theta - f_{s} & = m(a_{CM}) x, \\ N - mg \cos \theta & = 0 \end{split}\]

podemos então resolver a aceleração linear do centro de massa a partir dessas equações:

\[a_{CM} = g\sin \theta - \frac{f_s}{m} \ldotp\]

No entanto, é útil expressar a aceleração linear em termos do momento de inércia. Para isso, escrevemos a segunda lei de rotação de Newton,

\[\sum \tau_{CM} = I_{CM} \alpha \ldotp\]

Os torques são calculados em torno do eixo que passa pelo centro de massa do cilindro. O único torque diferente de zero é fornecido pela força de atrito. Nós temos

\[f_{s} r = I_{CM} \alpha \ldotp\]

Finalmente, a aceleração linear está relacionada à aceleração angular por

\[(a_{CM})_{x} = r \alpha \ldotp\]

Essas equações podem ser usadas para resolver um _CM,$\alpha$, e f _S em termos do momento de inércia, onde eliminamos o subíndice x. Escrevemos um _CM em termos do componente vertical da gravidade e da força de atrito e fazemos as seguintes substituições.

\[f_{S} = \frac{I_{CM} \alpha}{r} = \frac{I_{CM} a_{CM}}{r^{2}}\]

A partir disso, obtemos

\[\begin{split} a_{CM} & = g \sin \theta - \frac{I_{CM} a_{CM}}{mr^{2}}, \\ & = \frac{mg \sin \theta}{m + \left(\dfrac{I_{CM}}{r^{2}}\right)} \ldotp \end{split}\]

Observe que esse resultado é independente do coeficiente de atrito estático,$\mu_{s}$.

Como temos um cilindro sólido, da Figura 10.5.4, temos I _CM =$\frac{mr^{2}}{2}$ e

\[a_{CM} = \frac{mg \sin \theta}{m + \left(\dfrac{mr^{2}}{2r^{2}}\right)} = \frac{2}{3} g \sin \theta \ldotp\]

Portanto, temos

\[\alpha = \frac{a_{CM}}{r} = \frac{2}{3r} g \sin \theta \ldotp\]

Como o deslizamento não ocorre, f _S ≤$\mu_{s}$ N. Resolvendo a força de atrito, $$f_ {s} = I_ {CM}\ frac {\ alpha} {r} = I_ {CM}\ frac {(a_ {CM})} {r^ {2}} =\ left (\ dfrac {I_ {CM}} {r^ {2}}\ right)\ left (\ dfrac {I_ {CM}} {r^ {2}}\ right)\ left (\ dfrac {I_ {CM}} {r^ {2}}\ right)\ left (\ dfradfrac {mg\ sin\ theta} {m +\ left (\ dfrac {I_ {CM}} {r^ {2}}\ direita)}\ direita) =\ frac {mg I_ {CM}\ sin\ theta} {mr^ {2} + I_ {CM}}\ LDOTP$$ Substituindo essa expressão na condição para não escorregar, e observando que N = mg cos$\theta$, temos $$\ frac {mg I_ {CM}\ sin\ theta} {mr^ {2} + I_ {CM}}\ leq\ mu_ {s} mg\ cos\ theta$ou $$\ mu_ {s}\ geq\ frac {\ tan\ theta} {1 +\ left (\ dfrac {mr^ {2}} {I_ {CM}}\ right)}\ ldotp$$para o sólido cilindro, isso se torna $$\ mu_ {s}\ geq\ frac {\ tan\ theta} {1 +\ left (\ dfrac {2mr^ {2}} {mr^ {2}}\ right)} =\ frac {1} {3}\ tan\ theta\ ldotp$$

Significância

A aceleração linear é linearmente proporcional ao pecado$\theta$. Assim, quanto maior o ângulo da inclinação, maior a aceleração linear, como seria de se esperar. A aceleração angular, entretanto, é linearmente proporcional ao pecado$\theta$ e inversamente proporcional ao raio do cilindro. Assim, quanto maior o raio, menor a aceleração angular.
Para que não ocorra escorregamento, o coeficiente de atrito estático deve ser maior ou igual a$\frac{1}{3}$ tan$\theta$. Assim, quanto maior o ângulo de inclinação, maior deve ser o coeficiente de atrito estático para evitar que o cilindro escorregue.

Exercício$\PageIndex{2}$

Um cilindro oco está inclinado em um ângulo de 60°. O coeficiente de atrito estático na superfície é$\mu_{s}$ = 0,6. (a) O cilindro rola sem escorregar? (b) Um cilindro sólido rolará sem escorregar?

Vale a pena repetir a equação derivada neste exemplo para a aceleração de um objeto rolando sem escorregar:

\[a_{CM} = \frac{mg \sin \theta}{m + \left(\dfrac{I_{CM}}{r^{2}}\right)} \ldotp \label{11.4}\]

Essa é uma equação muito útil para resolver problemas envolvendo rolar sem escorregar. Observe que a aceleração é menor do que a de um objeto deslizando por um plano sem atrito sem rotação. A aceleração também será diferente para dois cilindros rotativos com diferentes inércias rotacionais.

Movimento de rolamento com deslizamento

No caso de movimento de rolamento com escorregamento, devemos usar o coeficiente de atrito cinético, que dá origem à força de atrito cinético, pois o atrito estático não está presente. A situação é mostrada na Figura$\PageIndex{5}$. No caso de escorregamento, v _CM − R$\omega$ ≠ 0, porque o ponto P na roda não está em repouso na superfície, e v _P ≠ 0. Assim,$\omega$ ≠$\frac{v_{CM}}{R}$,$\alpha \neq \frac{a_{CM}}{R}$.

Exemplo$\PageIndex{2}$: Rolling Down an Inclined Plane with Slipping

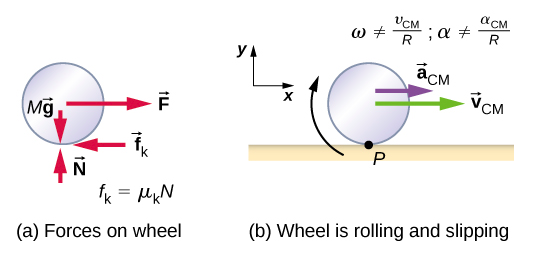
Um cilindro sólido desce de um plano inclinado do repouso e sofre escorregões (Figura$\PageIndex{6}$). Tem massa m e raio r. (a) Qual é sua aceleração linear? (b) Qual é sua aceleração angular em torno de um eixo que passa pelo centro de massa?

Estratégia

Desenhe um esboço e um diagrama de corpo livre mostrando as forças envolvidas. O diagrama de corpo livre é semelhante ao da caixa antiderrapante, exceto pela força de atrito, que é cinética em vez de estática. Use a segunda lei de Newton para resolver a aceleração na direção x. Use a segunda lei de rotação de Newton para resolver a aceleração angular.

Solução

Um diagrama de um cilindro rolando e deslizando por um plano inclinado e um diagrama de corpo livre do cilindro. À esquerda está uma ilustração mostrando o plano inclinado, que forma um ângulo de teta com a horizontal. Mostra-se que o cilindro está em repouso na parte superior e, em seguida, se movendo ao longo da inclinação quando está mais baixo. À direita está um diagrama corporal gratuito. O sistema de coordenadas x y é inclinado de forma que a direção x positiva seja paralela ao plano inclinado e aponte para sua parte inferior, e a direção y positiva seja para fora, perpendicular ao plano. Quatro forças são mostradas. N j hat atua no centro do cilindro e aponta na direção y positiva. m g sine theta i hat atua no centro do cilindro e aponta na direção x positiva. Menos m g cosseno theta j hat atua no centro do cilindro e aponta na direção y negativa. Menos f sub k i que atua no ponto de contato e aponta na direção negativa x. — Figura$\PageIndex{6}$: Um cilindro sólido desce de um plano inclinado do repouso e sofre escorregões. O sistema de coordenadas tem x na direção abaixo do plano inclinado e y para cima perpendicular ao plano. O diagrama de corpo livre mostra a força normal, a força de atrito cinético e os componentes do peso$\vec{g}$ m.

A soma das forças na direção y é zero, então a força de atrito agora é f _k =$\mu_{k}$ N =$\mu_{k}$ mg cos$\theta$. A segunda lei de Newton na direção x se torna

\[\sum F_{x} = ma_{x}, \nonumber\]

\[mg \sin \theta - \mu_{k} mg \cos \theta = m(a_{CM})_{x}, \nonumber\]

\[(a_{CM})_{x} = g(\sin \theta - \mu_{k} \cos \theta) \ldotp \nonumber\]

A força de atrito fornece o único torque em torno do eixo através do centro de massa, então a segunda lei de rotação de Newton se torna

\[\sum \tau_{CM} = I_{CM} \alpha, \nonumber\]

\[f_{k} r = I_{CM} \alpha = \frac{1}{2} mr^{2} \alpha \ldotp \nonumber\]

Resolvendo para$\alpha$, temos

\[\alpha = \frac{2f_{k}}{mr} = \frac{2 \mu_{k} g \cos \theta}{r} \ldotp \nonumber\]

Significância

Escrevemos as acelerações lineares e angulares em termos do coeficiente de atrito cinético. A aceleração linear é a mesma encontrada para um objeto deslizando por um plano inclinado com atrito cinético. A aceleração angular em torno do eixo de rotação é linearmente proporcional à força normal, que depende do cosseno do ângulo de inclinação. Em$\theta$ → 90°, essa força vai para zero e, portanto, a aceleração angular vai para zero.

Conservação de energia mecânica em movimento de rolamento

No capítulo anterior, introduzimos a energia cinética rotacional. Qualquer objeto rolante carrega energia cinética rotacional, bem como energia cinética translacional e energia potencial, se o sistema exigir. Incluindo a energia potencial gravitacional, a energia mecânica total de um objeto rolando é

\[E_{T} = \frac{1}{2} mv^{2}_{CM} + \frac{1}{2} I_{CM} \omega^{2} + mgh \ldotp\]

Na ausência de forças não conservadoras que retirem energia do sistema na forma de calor, a energia total de um objeto rolante sem escorregar é conservada e é constante durante todo o movimento. Exemplos em que a energia não é conservada são um objeto rolante que está escorregando, produção de calor como resultado do atrito cinético e um objeto rolante que encontra resistência ao ar.

Você pode perguntar por que um objeto rolante que não está escorregando economiza energia, já que a força de atrito estática não é conservadora. A resposta pode ser encontrada consultando a Figura$\PageIndex{2}$. O ponto P em contato com a superfície está em repouso em relação à superfície. Portanto, seu deslocamento infinitesimal d em$\vec{r}$ relação à superfície é zero e o trabalho incremental realizado pela força estática de atrito é zero. Podemos aplicar a conservação de energia ao nosso estudo do movimento de rolamento para obter alguns resultados interessantes.

Exemplo$\PageIndex{3}$: Curiosity Rover

O rover Curiosity, mostrado na Figura$\PageIndex{7}$, foi implantado em Marte em 6 de agosto de 2012. As rodas do rover têm um raio de 25 cm. Suponha que os astronautas cheguem a Marte no ano de 2050 e encontrem o agora inoperante Curiosity na lateral de uma bacia. Enquanto eles estão desmontando o rover, um astronauta perde acidentalmente a aderência em uma das rodas, que rola sem escorregar até o fundo da bacia 25 metros abaixo. Se a roda tiver uma massa de 5 kg, qual é a velocidade na parte inferior da bacia?

Uma fotografia do rover Curiosity da NASA durante testes no Laboratório de Propulsão a Jato. — Figura$\PageIndex{7}$: O rover Curiosity do Laboratório Científico de Marte da NASA durante testes em 3 de junho de 2011. O local é dentro da Instalação de Montagem de Naves Espaciais no Laboratório de Propulsão a Jato da NASA em Pasadena, Califórnia. (crédito: NASA/JPL-Caltech)

Estratégia

Usamos a conservação mecânica de energia para analisar o problema. No topo da colina, a roda está em repouso e tem apenas energia potencial. No fundo da bacia, a roda tem energia cinética rotacional e translacional, que deve ser igual à energia potencial inicial por conservação de energia. Como a roda está rolando sem escorregar, usamos a relação v _CM = r$\omega$ para relacionar as variáveis translacionais às variáveis rotacionais na equação de conservação de energia. Em seguida, resolvemos a velocidade. Na Figura$\PageIndex{7}$, vemos que um cilindro oco é uma boa aproximação para a roda, então podemos usar esse momento de inércia para simplificar o cálculo.

Solução

A energia no topo da bacia é igual à energia na parte inferior:

\[mgh = \frac{1}{2} mv_{CM}^{2} + \frac{1}{2} I_{CM} \omega^{2} \ldotp \nonumber\]

As quantidades conhecidas são I _CM = mr ², r = 0,25 m e h = 25,0 m.

Nós reescrevemos a equação de conservação de energia$\omega$ eliminando usando$\omega$ = v _CM r. Nós temos

\[mgh = \frac{1}{2} mv_{CM}^{2} + \frac{1}{2} mr^{2} \frac{v_{CM}^{2}}{r^{2}} \nonumber\]

\[gh = \frac{1}{2} v_{CM}^{2} + \frac{1}{2} v_{CM}^{2} \Rightarrow v_{CM} = \sqrt{gh} \ldotp \nonumber\]

Em Marte, a aceleração da gravidade é de 3,71 m/s ², o que dá a magnitude da velocidade no fundo da bacia como

\[v_{CM} = \sqrt{(3.71\; m/s^{2})(25.0\; m)} = 9.63\; m/s \ldotp \nonumber\]

Significância

Esse é um resultado bastante preciso, considerando que Marte tem muito pouca atmosfera e a perda de energia devido à resistência do ar seria mínima. O resultado também pressupõe que o terreno seja liso, de forma que a roda não encontre pedras e solavancos ao longo do caminho.

Além disso, neste exemplo, a energia cinética, ou energia do movimento, é igualmente compartilhada entre o movimento linear e o rotacional. Se observarmos os momentos de inércia na Figura 10.5.4, vemos que o cilindro oco tem o maior momento de inércia para um determinado raio e massa. Se as rodas do rover fossem sólidas e aproximadas por cilindros sólidos, por exemplo, haveria mais energia cinética no movimento linear do que no movimento rotacional. Isso daria à roda uma velocidade linear maior do que a aproximação do cilindro oco. Assim, o cilindro sólido alcançaria o fundo da bacia mais rápido do que o cilindro oco.

Exemplo\(\PageIndex{1}\): Rolling Down an Inclined Plane

Solução

Exercício\(\PageIndex{2}\)

Exemplo\(\PageIndex{2}\): Rolling Down an Inclined Plane with Slipping

Solução

Exemplo\(\PageIndex{3}\): Curiosity Rover

Solução