10.6: Circuitos RC
- Page ID
- 184528
Ao final da seção, você poderá:
- Descreva o processo de carregamento de um capacitor
- Descreva o processo de descarga de um capacitor
- Listar algumas aplicações de circuitos RC
Quando você usa uma câmera com flash, leva alguns segundos para carregar o capacitor que alimenta o flash. O flash de luz descarrega o capacitor em uma pequena fração de segundo. Por que o carregamento demora mais do que o descarregamento? Essa questão e vários outros fenômenos que envolvem carregar e descarregar capacitores são discutidos neste módulo.
Circuitos com resistência e capacitância
Um circuito RC é um circuito que contém resistência e capacitância. Conforme apresentado em Capacitância, o capacitor é um componente elétrico que armazena carga elétrica, armazenando energia em um campo elétrico.
\(\PageIndex{1a}\)A figura mostra um circuito RC simples que emprega uma fonte de tensão DC (corrente contínua)\(ε\), um resistor\(R\), um capacitor\(C\) e uma chave de duas posições. O circuito permite que o capacitor seja carregado ou descarregado, dependendo da posição do interruptor. Quando o interruptor é movido para a posição\(A\), o capacitor carrega, resultando no circuito na Figura\(\PageIndex{1b}\). Quando o interruptor é movido para a posição B, o capacitor é descarregado através do resistor.
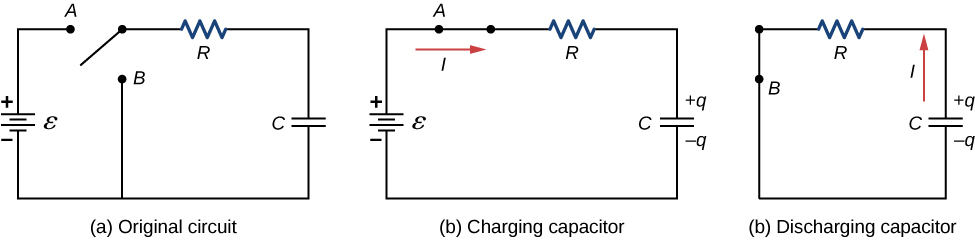
Carregando um capacitor
Podemos usar a regra de loop de Kirchhoff para entender o carregamento do capacitor. Isso resulta na equação\(\epsilon - V_R - V_C = 0\). Essa equação pode ser usada para modelar a carga em função do tempo em que o capacitor carrega. A capacitância é definida como\(C = q/V\), portanto, a tensão no capacitor é\(V_C = \frac{q}{C}\). Usando a lei de Ohm, a queda potencial no resistor é\(V_R = IR\), e a corrente é definida como\(I = dq/dt\).
\[\epsilon - V_R - V_C =0,\]
\[\epsilon - IR - \frac{q}{C} = 0,\]
\[\epsilon - R\frac{dq}{dt} - \frac{q}{C} = 0.\]
Essa equação diferencial pode ser integrada para encontrar uma equação para a carga no capacitor em função do tempo.
\[\epsilon - R\frac{dq}{dt} - \frac{q}{C} = 0.\]
\[\frac{dq}{dt} = \frac{\epsilon C - q}{RC},\]
\[\int_0^q \frac{dq}{\epsilon C - q} = \frac{1}{RC} \int_0^t dt.\]
Deixe\(u = \epsilon C - q\), então\(du = -dq\). O resultado é
\[-\int_0^q \frac{du}{u} = \frac{1}{RC} \int_0^t dt,\]
\[\ln \left(\frac{\epsilon C - q}{\epsilon C}\right) = - \frac{1}{RC} t.\]
\[\frac{\epsilon C - q}{\epsilon C} = e^{-t/RC}.\]
A simplificação resulta em uma equação para a carga no capacitor de carregamento em função do tempo:
\[q(t) = C\epsilon \left(1 - e^{-\frac{t}{RC}}\right) = Q\left(1 - e^{-\frac{t}{\tau}}\right).\]
Um gráfico da carga no capacitor em relação ao tempo é mostrado na Figura\(\PageIndex{2a}\). Primeiro, observe que quando o tempo se aproxima do infinito, o exponencial vai para zero, então a carga se aproxima da carga máxima\(Q = C\epsilon\) e tem unidades de coulombs. As unidades de RC são segundos, unidades de tempo. Essa quantidade é conhecida como constante de tempo:
\[\tau = RC.\]
Por vez\(t = \tau = RC\), a carga é igual à\(1 - e^{-1} = 1 - 0.368 = 0.632\) carga máxima\(Q = C\epsilon\). Observe que a variação da taxa de tempo da carga é a inclinação em um ponto da carga versus o gráfico de tempo. A inclinação do gráfico é grande no tempo\(t - 0.0 \, s\) e se aproxima de zero à medida que o tempo aumenta.
Conforme a carga no capacitor aumenta, a corrente através do resistor diminui, conforme mostrado na Figura\(\PageIndex{2b}\). A corrente através do resistor pode ser encontrada tomando a derivada temporal da carga.
\[ \begin{align*} I(t) &= \frac{dq}{dt} \\[4pt] &= \frac{d}{dt}\left[C\epsilon \left( 1 - e^{-\frac{t}{RC}} \right) \right], \\[4pt] &= C\epsilon \left(\frac{1}{RC}\right) e^{-\frac{t}{RC}} \\[4pt] &= \frac{\epsilon}{R} e^{-\frac{t}{TC}} \\[4pt] &= I_0 e^{-\frac{t}{RC}}, \end{align*}\]
\[I(t) = I_0 e^{-t/\tau}.\]
No momento\(t = 0.0 \, s\), a corrente através do resistor é\(I_0 = \frac{\epsilon}{R}\). Conforme o tempo se aproxima do infinito, a corrente se aproxima de zero. No momento\(t = \tau\), a corrente através do resistor é\(I (t = \tau) = I_0e^{-1} = 0.368 I_0\).
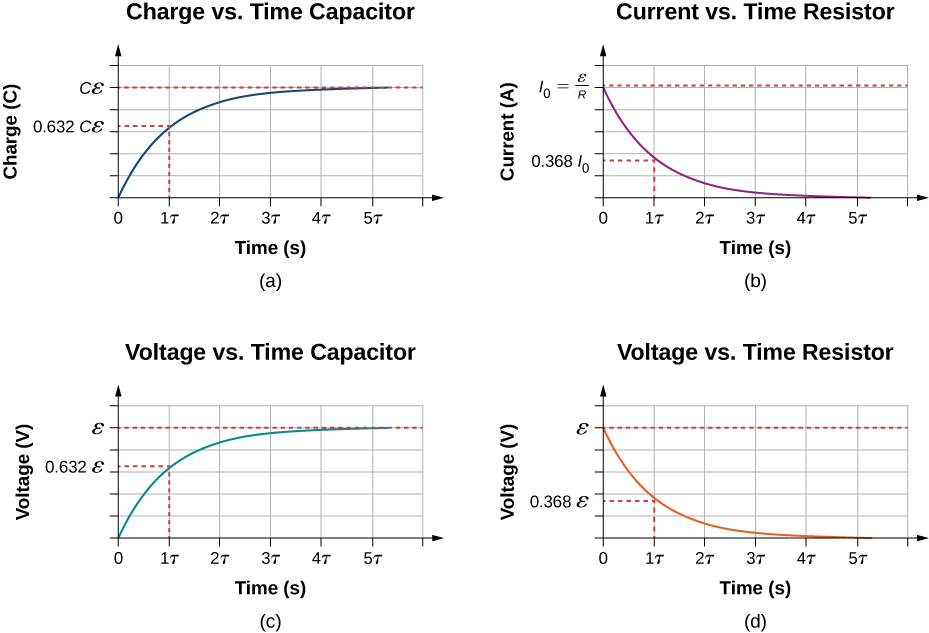
As figuras\(\PageIndex{2c}\) e figuras\(\PageIndex{2d}\) mostram as diferenças de tensão entre o capacitor e o resistor, respectivamente. Conforme a carga no capacitor aumenta, a corrente diminui, assim como a diferença de tensão no resistor\(V_R(t) = (I_0R)e^{-t/\tau} = \epsilon e^{-t/\tau}\). A diferença de tensão entre o capacitor aumenta à medida que\(V_C (t) = \epsilon (1 - e^{-t/\tau} )\).
Descarregando um capacitor
Quando o interruptor na Figura\(\PageIndex{3a}\) é movido para a posição B, o circuito é reduzido para o circuito em parte (c) e o capacitor carregado pode ser descarregado através do resistor. Um gráfico da carga no capacitor em função do tempo é mostrado na Figura\(\PageIndex{3a}\). Usar a regra de loop de Kirchhoff para analisar o circuito à medida que o capacitor descarrega resulta na equação\(-V_R -V_C = 0\), que simplifica\(IR + \frac{q}{C} = 0\) a. Usar a definição de corrente\(\frac{dq}{dt}R = - \frac{q}{C}\) e integrar a equação do loop produz uma equação para a carga no capacitor em função do tempo:
\[q(t) = Qe^{-t/\tau}.\]
Aqui, Q é a carga inicial no capacitor e\(\tau = RC\) é a constante de tempo do circuito. Conforme mostrado no gráfico, a carga diminui exponencialmente em relação à carga inicial, aproximando-se de zero quando o tempo se aproxima do infinito.
A corrente em função do tempo pode ser encontrada tomando a derivada temporal da carga:
\[I(t) = - \frac{Q}{RC}e^{-t/\tau}.\]
O sinal negativo mostra que a corrente flui na direção oposta à corrente encontrada quando o capacitor está carregando. A figura\(\PageIndex{3b}\) mostra um exemplo de um gráfico de carga versus tempo e corrente versus tempo. Um gráfico da diferença de tensão entre o capacitor e a diferença de tensão no resistor em função do tempo é mostrado nas Figuras\(\PageIndex{3c}\)\(\PageIndex{3d}\) e. Observe que as magnitudes da carga, corrente e tensão diminuem exponencialmente, aproximando-se de zero à medida que o tempo aumenta.
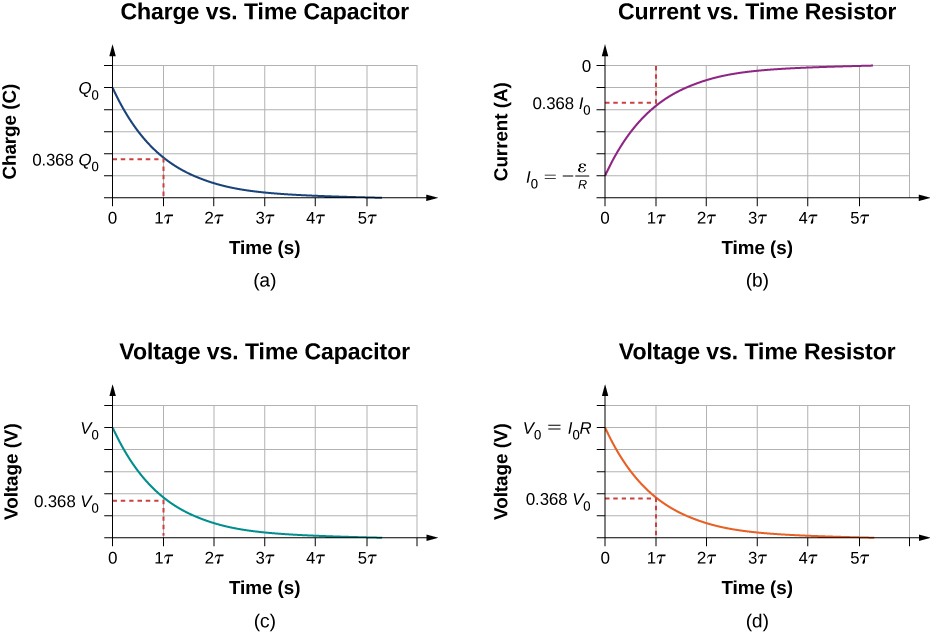
Agora, podemos explicar por que a câmera flash mencionada no início desta seção leva muito mais tempo para carregar do que para descarregar: a resistência durante o carregamento é significativamente maior do que durante a descarga. A resistência interna da bateria é responsável pela maior parte da resistência durante o carregamento. Conforme a bateria envelhece, o aumento da resistência interna torna o processo de carregamento ainda mais lento.
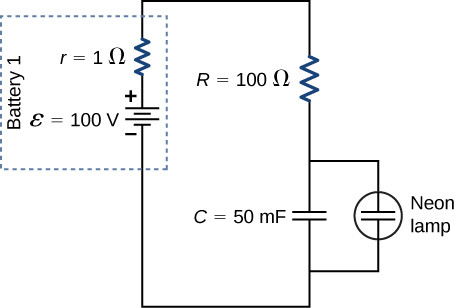
Uma aplicação de um circuito RC é o oscilador de relaxamento, conforme mostrado abaixo. O oscilador de relaxamento consiste em uma fonte de tensão, um resistor, um capacitor e uma lâmpada de néon. A lâmpada de néon age como um circuito aberto (resistência infinita) até que a diferença de potencial entre a lâmpada de néon atinja uma voltagem específica. Nessa voltagem, a lâmpada funciona como um curto-circuito (resistência zero), e o capacitor descarrega através da lâmpada de néon e produz luz. No oscilador de relaxamento mostrado, a fonte de tensão carrega o capacitor até que a tensão no capacitor seja de 80 V. Quando isso acontece, o néon da lâmpada se rompe e permite que o capacitor seja descarregado pela lâmpada, produzindo um flash brilhante. Depois que o capacitor é totalmente descarregado pela lâmpada de néon, ele começa a carregar novamente e o processo se repete. Supondo que o tempo que o capacitor leva para descarregar seja insignificante, qual é o intervalo de tempo entre os flashes?
Estratégia
O período de tempo pode ser encontrado considerando a equação\(V_C(t) = \epsilon (1 - e^{=t/\tau})\). where \(\tau = (R + r)C.\)
Solution
The neon lamp flashes when the voltage across the capacitor reaches 80 V. The RC time constant is equal to \(\tau = (R + r) = (101 \, \Omega) (50 \times 10^{-3} F) = 5.05 \, s\). We can solve the voltage equation for the time it takes the capacitor to reach 80 V:
\[V_C (t) = \epsilon (1 - e^{-t/\tau} ),\]
\[e^{-t/\tau} = 1 - \frac{V_C(t)}{\epsilon},\]
\[ln (e^{-t/\tau}) = ln \left(1 - \frac{V_C(t)}{\epsilon} \right),\]
\[t = -\tau ln \left(1 - \frac{V_C(t)}{\epsilon} \right) = -5.05 \, s \cdot ln \left(1 - \frac{80 \, V}{100 \, V} \right) = 8.13 \, s.\]
Significance
One application of the relaxation oscillator is for controlling indicator lights that flash at a frequency determined by the values for R and C. In this example, the neon lamp will flash every 8.13 seconds, a frequency of \( f = \frac{1}{T} = \frac{1}{8.13 \, s} = 0.55 \, Hz\). The relaxation oscillator has many other practical uses. It is often used in electronic circuits, where the neon lamp is replaced by a transistor or a device known as a tunnel diode. The description of the transistor and tunnel diode is beyond the scope of this chapter, but you can think of them as voltage controlled switches. They are normally open switches, but when the right voltage is applied, the switch closes and conducts. The “switch” can be used to turn on another circuit, turn on a light, or run a small motor. A relaxation oscillator can be used to make the turn signals of your car blink or your cell phone to vibrate.
RC circuits have many applications. They can be used effectively as timers for applications such as intermittent windshield wipers, pace makers, and strobe lights. Some models of intermittent windshield wipers use a variable resistor to adjust the interval between sweeps of the wiper. Increasing the resistance increases the RC time constant, which increases the time between the operation of the wipers.
Another application is the pacemaker. The heart rate is normally controlled by electrical signals, which cause the muscles of the heart to contract and pump blood. When the heart rhythm is abnormal (the heartbeat is too high or too low), pace makers can be used to correct this abnormality. Pacemakers have sensors that detect body motion and breathing to increase the heart rate during physical activities, thus meeting the increased need for blood and oxygen, and an RC timing circuit can be used to control the time between voltage signals to the heart.
Looking ahead to the study of ac circuits (Alternating-Current Circuits), ac voltages vary as sine functions with specific frequencies. Periodic variations in voltage, or electric signals, are often recorded by scientists. These voltage signals could come from music recorded by a microphone or atmospheric data collected by radar. Occasionally, these signals can contain unwanted frequencies known as “noise.” RC filters can be used to filter out the unwanted frequencies.
In the study of electronics, a popular device known as a 555 timer provides timed voltage pulses. The time between pulses is controlled by an RC circuit. These are just a few of the countless applications of RC circuits.
A relaxation oscillator is used to control a pair of windshield wipers. The relaxation oscillator consists of a 10.00-mF capacitor and a \(10.00 \, k\Omega\) variable resistor known as a rheostat. A knob connected to the variable resistor allows the resistance to be adjusted from \(0.00 \, \Omega\) to \(10.00 \, k\Omega\). The output of the capacitor is used to control a voltage-controlled switch. The switch is normally open, but when the output voltage reaches 10.00 V, the switch closes, energizing an electric motor and discharging the capacitor. The motor causes the windshield wipers to sweep once across the windshield and the capacitor begins to charge again. To what resistance should the rheostat be adjusted for the period of the wiper blades be 10.00 seconds?
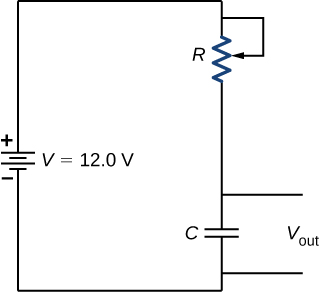
Estratégia
A resistência considera a equação\(V_{out}(t) = V(1 - e^{-t/\tau})\), onde\(\tau = RC\). A capacitância, a tensão de saída e a tensão da bateria são fornecidas. Precisamos resolver essa equação para a resistência.
Solução
A tensão de saída será de 10,00 V e a voltagem da bateria será de 12,00 V. A capacitância é dada como 10,00 mF. Resolvendo os rendimentos de resistência
\[V_{out}(t) = V(1 - e^{-t/\tau})\]
\[e^{-t/RC} = 1 - \frac{V_{out}(t)}{V},\]
\[ln (e^{-t/RC}) = ln \left(1 - \frac{V_{out}(t)}{V} \right),\]
\[-\frac{t}{RC} = ln \left(1 - \frac{V_{out}(t)}{V} \right),\]
\[R = \frac{-t}{C \, ln\left( 1 - \frac{V_C(t)}{V}\right)} = \frac{-10.00 \, s}{10 \times 10^{-3} F \, ln \left(1 - \frac{10 \, V}{12 \, V}\right)} = 558.11 \, \Omega.\]
Significância
Aumentar a resistência aumenta o tempo de atraso entre as operações dos limpadores de para-brisa. Quando a resistência é zero, os limpadores de para-brisa funcionam continuamente. Na resistência máxima, o período de operação dos limpadores é:
\[t = -RC ln\left(1 - \frac{V_{out}(t)}{V}\right) = - (10 \times 10^{-3} F)(10 \times 10^3 \, \Omega) ln \left(1 - \frac{10 \, V}{12 \, V}\right) = 179.18 \, s = 2.98 \, min.\]
O circuito RC tem milhares de usos e é um circuito muito importante para estudar. Não só pode ser usado para cronometrar circuitos, mas também pode ser usado para filtrar frequências indesejadas em um circuito e usado em fontes de alimentação, como a do seu computador, para ajudar a transformar a tensão CA em tensão contínua.


