33.E: Relatividade Especial (Exercício)
- Page ID
- 194541
Perguntas conceituais
33.3: Aceleradores criam matéria a partir da energia
1. A energia total no feixe de um acelerador é muito maior do que a energia das partículas individuais do feixe. Por que essa energia total não está disponível para criar uma única partícula extremamente massiva?
2. A radiação síncrotron retira energia de um feixe acelerador e está relacionada à aceleração. Por que você esperaria que o problema fosse mais grave para aceleradores de elétrons do que para aceleradores de prótons?
3. Quais são as duas principais limitações que nos impedem de construir aceleradores de alta energia que são fisicamente pequenos?
4. Quais são as vantagens dos aceleradores de feixe de colisão? Quais são as desvantagens?
33.4: Partículas, padrões e leis de conservação
5. Grandes quantidades de antimatéria isolada da matéria normal devem se comportar exatamente como matéria normal. Um antiátomo, por exemplo, composto de pósitrons, antiprótons e antineutrons deve ter o mesmo espectro atômico de sua contraparte de matéria. Você seria capaz de dizer que é antimatéria pela emissão de antifótons? Explique brevemente.
6. Partículas sem massa não são apenas neutras, elas não têm carga (ao contrário do nêutron). Por que isso é assim?
7. Partículas sem massa devem viajar à velocidade da luz, enquanto outras não podem atingir essa velocidade. Por que todas as partículas sem massa são estáveis? Se forem encontradas evidências de que os neutrinos se decompõem espontaneamente em outras partículas, isso implicaria que eles têm massa?
8. Quando uma estrela entra em erupção em uma explosão de supernova, um grande número de neutrinos de elétrons é formado em reações nucleares. Esses neutrinos da supernova de 1987A na relativamente próxima Nuvem de Magalhães foram observados poucas horas após o brilho inicial, indicando que eles viajaram para a Terra aproximadamente à velocidade da luz. Explique como esses dados podem ser usados para definir um limite superior na massa do neutrino, observando que, se a massa for pequena, os neutrinos podem viajar muito perto da velocidade da luz e ter uma energia razoável (na ordem de MeV).
9. Os teóricos tiveram um sucesso espetacular ao prever partículas até então desconhecidas. Considerando os triunfos teóricos do passado, por que devemos nos preocupar em realizar experimentos?
10. Que tempo de vida você espera de um antineutron isolado da matéria normal?
11. Por que o\(\displaystyle η^0\) méson tem uma vida útil tão curta em comparação com a maioria dos outros mésons?
12. (a) Um hádron é sempre um barião?
(b) Um bárion é sempre um hádron?
(c) Um barião instável pode se decompor em um méson, não deixando nenhum outro bárion?
13. Explique como a conservação do número bariônico é responsável pela conservação da massa atômica total (número total de núcleons) no decaimento e nas reações nucleares.
33.5: Quarks: Isso é tudo o que existe?
14. A mudança de sabor do quark\(\displaystyle d→u\) ocorre em\(\displaystyle β^−\) decomposição. Isso significa que a mudança reversa do sabor do quark\(\displaystyle u→d\) ocorre em\(\displaystyle β^+\) decomposição? Justifique sua resposta escrevendo o decaimento em termos dos constituintes do quark, observando que parece que um próton é convertido em nêutron no decaimento β+.
15. Explique como a força fraca pode mudar a estranheza ao alterar o sabor do quark.
16. O decaimento beta é causado pela força fraca, assim como todas as reações nas quais a estranheza muda. Isso implica que a força fraca pode mudar o sabor do quark? Explique.
17. Por que é mais fácil ver as propriedades dos quarks c, b e t em mésons com composição\(\displaystyle W^−\) ou em\(\displaystyle t\bar{t}\) vez de em bárions com uma mistura de quarks, como\(\displaystyle udb\)?
18. Como os quarks, que são férmions, podem se combinar para formar bósons? Por que um número par deve se combinar para formar um bóson? Dê um exemplo declarando a subestrutura de quarks de um bóson.
19. Quais evidências são citadas para apoiar a alegação de que a força do glúon entre os quarks é maior do que a força nuclear forte entre os hádrons? Como isso está relacionado à cor? Também está relacionado ao confinamento de quarks?
20. Discuta como sabemos que não\(\displaystyle π-mesons (π^+,π,π^0)\) são partículas fundamentais e não são portadoras básicas da força forte.
21. Um antibário tem três antiquarks com cores\(\displaystyle \bar{R}\bar{G}\bar{B}\). Qual é a cor dela?
22. Suponha que os léptons sejam criados em uma reação. Isso implica que a força fraca está agindo? (por exemplo, considere a\(\displaystyle β\) decadência.)
23. Como a vida útil de uma partícula pode indicar que sua decomposição é causada pela forte força nuclear? Como uma mudança na estranheza pode implicar qual força é responsável por uma reação? O que uma mudança no sabor do quark implica na força responsável?
24. (a) Todas as partículas com estranheza também têm pelo menos um quark estranho?
(b) Todos os hádrons com um quark estranho também têm estranheza diferente de zero?
25. A partícula sigma-zero decai principalmente por meio da reação\(\displaystyle \sum{}^0→Λ^0+γ\). Explique como esse decaimento e as respectivas composições de quarks implicam que o\(\displaystyle \sum{}^0\) é um estado excitado do\(\displaystyle Λ^0\).
26. O que as composições de quarks e outros números quânticos implicam sobre as relações entre o\(\displaystyle Δ^+\) e o próton? O\(\displaystyle Δ^0\) e o nêutron?
27. Discuta as semelhanças e diferenças entre o fóton e o\(\displaystyle Z^0\) em termos das propriedades das partículas, incluindo as forças sentidas.
28. Identifique evidências de unificação eletrofraca.
29. Os quarks em uma partícula são confinados, o que significa que quarks individuais não podem ser observados diretamente. Os glúons também estão confinados? Explique
33.6: Grandes Teorias Unificadas
30. Se um GUT for comprovado e as quatro forças estiverem unificadas, ainda será correto dizer que a órbita da lua é determinada pela força gravitacional. Explique o porquê.
31. Se o bóson de Higgs for descoberto e descobrir que tem massa, ele será considerado o portador supremo da força fraca? Explique sua resposta.
32. Os glúons e o fóton não têm massa. Isso implica que os\(\displaystyle W^+, W^−\) e\(\displaystyle Z^0\) são os portadores definitivos da força fraca?
Problemas e exercícios
33.1: A partícula de Yukawa e o princípio da incerteza de Heisenberg revisitados
33. Uma partícula virtual com uma massa aproximada de\(\displaystyle 10^{14}GeV/c^2\) pode estar associada à unificação das forças fortes e eletrofracas. Por quanto tempo essa partícula virtual poderia existir (em violação temporária da conservação da energia de massa, conforme permitido pelo princípio da incerteza de Heisenberg)?
Solução
\(\displaystyle 3×10^{−39}s\)
34. Calcule a massa in\(\displaystyle GeV/c^2\) de uma partícula transportadora virtual que tem um alcance limitado a\(\displaystyle 10^{−30}\) m pelo princípio da incerteza de Heisenberg. Essa partícula pode estar envolvida na unificação das forças fortes e eletrofracas.
35. Outro componente da força nuclear forte é transmitido pela troca de mésons K virtuais. Considerando que os mésons K têm uma massa média de\(\displaystyle 495MeV/c^2\), qual é o alcance aproximado desse componente da força forte?
Solução
\(\displaystyle 1.99×10^{−16}m(0.2fm)\)
33.2: As Quatro Forças Básicas
36. (a) Encontre a razão entre as forças das forças fracas e eletromagnéticas em circunstâncias normais.
(b) O que essa proporção se torna em circunstâncias em que as forças são unificadas?
Solução
(a)\(\displaystyle 10^{−11}\) para 1, fraca para EM
(b) 1 a 1
37. A razão entre a força forte e a força fraca e a razão entre a força forte e a força eletromagnética se tornam 1 em circunstâncias em que elas são unificadas. Quais são as proporções entre a força forte e essas duas forças em circunstâncias normais?
33.3: Aceleradores criam matéria a partir da energia
38. Com energia total, os prótons no síncrotron Fermilab de 2,00 km de diâmetro viajam quase à velocidade da luz, já que sua energia é cerca de 1000 vezes a energia de massa restante.
(a) Quanto tempo um próton leva para completar uma viagem?
(b) Quantas vezes por segundo ele passará pela área alvo?
Solução
(a)\(\displaystyle 2.09×10^{−5}s\)
(b)\(\displaystyle 4.77×10^4Hz\)
39. Suponha que um\(\displaystyle W^−\) criado em uma câmara de bolhas viva para\(\displaystyle 5.00×10^{−25}s\). Que distância ele se move nesse tempo se estiver viajando a 0,900 c? Como essa distância é muito curta para fazer uma trilha, a presença do\(\displaystyle W^−\) deve ser inferida a partir de seus produtos de decaimento. Observe que o tempo é maior do que a\(\displaystyle W^−\) vida útil fornecida, o que pode ser devido à natureza estatística do decaimento ou da dilatação do tempo.
40. Qual é o comprimento de uma trilha que\(\displaystyle π^+\) viaja a 0,100 c deixa em uma câmara de bolhas se ela é criada lá e vive\(\displaystyle 2.60×10^{−8}s\)? (Aqueles que se movem mais rápido ou vivem mais tempo podem escapar do detector antes de se decompor.)
Solução
78,0 cm
41. O SLAC de 3,20 km de comprimento produz um feixe de elétrons de 50,0 GeV. Se houver 15.000 tubos de aceleração, qual tensão média deve estar nos espaços entre eles para obter essa energia?
42. Devido à perda de energia devido à radiação síncrotron no LHC no CERN, apenas 5,00 MeV são adicionados à energia de cada próton durante cada rotação ao redor do anel principal. Quantas revoluções são necessárias para produzir prótons de 7,00 TeV (7000 GeV), se forem injetados com uma energia inicial de 8,00 GeV?
Solução
\(\displaystyle 1.40×10^6\)
43. Um próton e um antipróton colidem de frente, cada um com uma energia cinética de 7,00 TeV (como no LHC no CERN). Quanta energia de colisão está disponível, levando em conta a aniquilação das duas massas? (Note que isso não é significativamente maior do que a energia cinética extremamente relativista.)
44. Quando um elétron e um pósitron colidem na instalação do SLAC, cada um deles tem energias cinéticas de 50,0 GeV. Qual é a energia total de colisão disponível, levando em consideração a energia de aniquilação? Note que a energia de aniquilação é insignificante, porque os elétrons são altamente relativistas.
Solução
100 GeV
33.4: Partículas, padrões e leis de conservação
45. O π 0 é sua própria antipartícula e decai da seguinte maneira:\(\displaystyle π^0→γ+γ\). Qual é a energia de cada\(\displaystyle γ\) raio se ele\(\displaystyle π^0\) estiver em repouso quando decai?
Solução
67,5 MeV
46. O modo de decaimento primário para o píon negativo é\(\displaystyle π^−→μ^−+\bar{ν_μ}\). Qual é a liberação de energia em MeV nesse decaimento?
47. A massa de uma partícula teórica que pode estar associada à unificação das forças eletrofracas e fortes é 1014GeV/C2.
(a) Quantas massas de prótons são essas?
(b) Quantas massas de elétrons são essas? (Isso indica o quão extremamente relativista o acelerador teria que ser para produzir a partícula e quão grande a quantidade relativista\(\displaystyle γ\) teria que ser.)
Solução
(a)\(\displaystyle 1×10^{14}\)
(b)\(\displaystyle 2×10^{17}\)
48. O modo de decaimento do múon negativo é\(\displaystyle μ^−→e^−+\bar{ν_e}+ν_μ\).
(a) Encontre a energia liberada em MeV.
(b) Verifique se os números da carga e da família leptônica estão conservados.
49. O modo de decaimento do tau positivo é\(\displaystyle τ^+→μ^++ν_μ+\bar{ν_τ}\).
(a) Qual energia é liberada?
(b) Verifique se os números da carga e da família leptônica estão conservados.
(c) O\(\displaystyle τ^+\) é a antipartícula do\(\displaystyle τ^−\) .Verifique se todos os produtos de decaimento do\(\displaystyle τ^+\) são as antipartículas daqueles na decadência do\(\displaystyle τ^−\) dado no texto.
Solução
(a) 1671 MeV
(b)\(\displaystyle Q=1,Q'=1+0+0=1.L_τ=−1;L'τ=−1;Lμ=0;L'μ=−1+1=0\)
(c)\(\displaystyle τ^−→μ^−+v_μ+\bar{v_τ}⇒μ^−\) antipartícula de\(\displaystyle μ^+; v_μ\) de\(\displaystyle \bar{v_μ}; \bar{v_τ}\) de\(\displaystyle v_τ\)
50. O principal modo de decaimento do sigma zero é\(\displaystyle \sum{}^0→Λ^0+γ\).
(a) Qual energia é liberada?
(b) Considerando a estrutura de quarks dos dois bárions, parece que o\(\displaystyle \sum{}^0\) é um estado excitado do\(\displaystyle Λ^0\)?
(c) Verifique se a estranheza, a carga e o número de bárions estão conservados na decadência.
(d) Considerando a vida útil anterior e a curta, a força fraca pode ser responsável? Declare por que ou por que não.
51. (a) Qual é a incerteza na energia liberada na decadência de a\(\displaystyle π^0\) devido à sua curta vida útil?
(b) Que fração da energia de decaimento é essa, observando que o modo de decaimento é\(\displaystyle π^0→γ+γ\) (para que toda a\(\displaystyle π^0\) massa seja destruída)?
Solução
(a) 3,9 eV
(b)\(\displaystyle 2.9×10^{−8}\)
52. (a) Qual é a incerteza na energia liberada na decadência de a\(\displaystyle τ^−\) devido à sua curta vida útil?
(b) A incerteza nessa energia é maior ou menor que a incerteza na massa do neutrino tau? Discuta a origem da incerteza.
33.5: Quarks: Isso é tudo o que existe?
53. (a) Verifique, a partir de sua composição de quarks, se a\(\displaystyle Δ^+\) partícula pode estar em um estado excitado do próton.
(b) Há uma propagação de cerca de 100 MeV na energia de decaimento do\(\displaystyle Δ^+\), interpretada como incerteza devido à sua curta vida útil. Qual é sua vida útil aproximada?
(c) Sua decadência ocorre por meio da força forte ou fraca?
Solução
(a) A\(\displaystyle uud\) composição é a mesma de um próton.
(b)\(\displaystyle 3.3×10^{−24}s\)
(c) Forte (vida útil curta)
54. Aceleradores como o Triangle Universities Meson Facility (TRIUMF) na Colúmbia Britânica produzem feixes secundários de píons fazendo com que um intenso feixe primário de prótons atinja um alvo. Essas “fábricas de mésons” têm sido usadas por muitos anos para estudar a interação de píons com núcleos e, portanto, a forte força nuclear. Uma reação que ocorre é\(\displaystyle π^++p→Δ^{++}→π^++p\), onde o\(\displaystyle Δ^{++}\) é uma partícula de vida muito curta. O gráfico na Figura mostra a probabilidade dessa reação em função da energia. A largura da protuberância é a incerteza de energia devido à curta vida útil do\(\displaystyle Δ^{++}\).
(a) Encontre esta vida.
(b) Verifique, a partir da composição dos quarks das partículas, se essa reação aniquila e, em seguida, recria um\(\displaystyle d\) quark e um\(\displaystyle \bar{d}\) antiquark escrevendo a reação e o decaimento em termos de quarks.
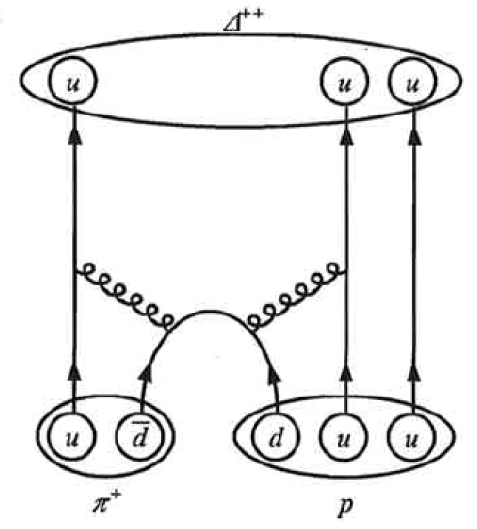
(c) Desenhe um diagrama de Feynman da produção e decaimento da\(\displaystyle Δ^{++}\) exibição dos quarks individuais envolvidos.
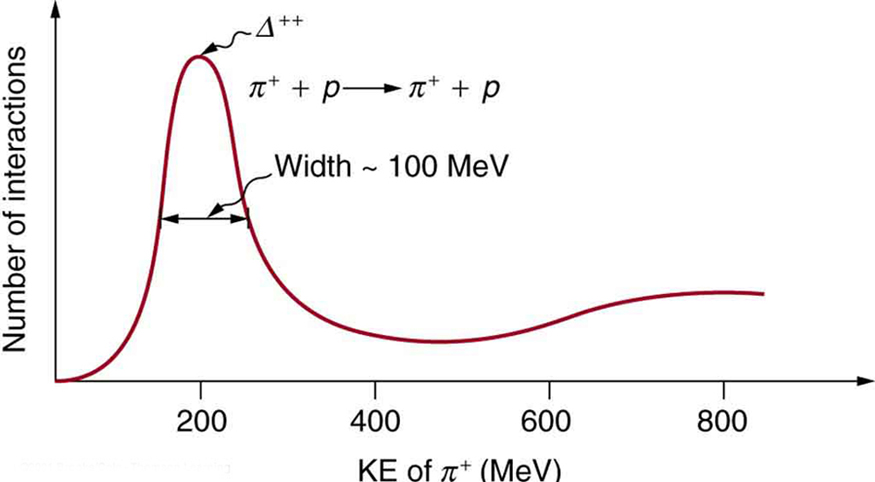
Este gráfico mostra a probabilidade de uma interação entre a\(\displaystyle π^+\) e um próton em função da energia. A colisão é interpretada como uma partícula de vida muito curta chamada de\(\displaystyle Δ^{++}\). A largura de aproximadamente 100 MeV da protuberância se deve à curta vida útil do\(\displaystyle Δ^{++}\).
55. A reação\(\displaystyle π^++p→Δ^{++}\) (descrita no problema anterior) ocorre por meio da força forte.
(a) Qual é o número bariônico da\(\displaystyle Δ^{++}\) partícula?
(b) Desenhe um diagrama de Feynman da reação mostrando os quarks individuais envolvidos.
Solução
a)\(\displaystyle Δ^{++}(uuu);B=\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=1\)
b)
56. Um dos modos de decaimento do ômega menos é\(\displaystyle Ω^−→Ξ^0+π^−\).
(a) Qual é a mudança na estranheza?
(b) Verifique se o número e a carga bariônica estão conservados, enquanto os números de léptons não são afetados.
(c) Escreva a equação em termos dos quarks constituintes, indicando que a força fraca é responsável.
57. Repita o problema anterior para o modo de decaimento\(\displaystyle Ω^−→Λ^0+K^−\).
Solução
(a)\(\displaystyle +1\)
(b)\(\displaystyle B=1=1+0, Z==0+(−1)\), todos os números de leptões são 0 antes e depois
(c)\(\displaystyle (sss)→(uds)+(\bar{u}s)\)
58. Um modo de decaimento para o méson eta-zero é\(\displaystyle η^0→γ+γ\).
(a) Encontre a energia liberada.
(b) Qual é a incerteza na energia devido à curta vida útil?
(c) Escreva o decaimento em termos dos quarks constituintes.
(d) Verifique se o número bariônico, os números de lépton e a carga estão conservados.
59. Um modo de decaimento para o méson eta-zero é\(\displaystyle η^0→π^0+π^0\).
(a) Escreva o decaimento em termos dos constituintes do quark.
(b) Quanta energia é liberada?
(c) Qual é a liberação final de energia, dado que o modo de decaimento para o pi zero é π 0→γ+γ?
Solução
(a)\(\displaystyle (u\bar{u}+d\bar{d})→(u\bar{u}+d\bar{d})+(u\bar{u}+d\bar{d})\)
(b) 277,9 MeV
(c) 547,9 MeV
60. A decadência é\(\displaystyle n→e^++e^−\) possível considerando as leis de conservação apropriadas? Declare por que ou por que não.
61. A decadência é\(\displaystyle μ^−→e^−+ν_e+ν_μ\) possível considerando as leis de conservação apropriadas? Declare por que ou por que não.
Solução
Não. \(\displaystyle Charge=−1\)é conservado. \(\displaystyle L_{e_i}=0≠L_{e_f}=2\)não é conservado. \(\displaystyle L_μ=1\)é conservado.
62. (a) A decadência é\(\displaystyle Λ^0→n+π^0\) possível considerando as leis de conservação apropriadas? Declare por que ou por que não.
(b) Escreva o decaimento em termos dos constituintes do quark das partículas.
63. (a) A decadência é\(\displaystyle \sum{}^−→n+π^−\) possível considerando as leis de conservação apropriadas? Declare por que ou por que não. (b) Escreva o decaimento em termos dos constituintes do quark das partículas.
Solução
(a) Sim. \(\displaystyle Z=−1=0+(−1), B=1=1+0\), todos os números da família leptônica são 0 antes e depois, espontâneos, pois a massa é maior antes da reação.
(b)\(\displaystyle dds→udd+\bar{u}d\)
64. A única combinação de cores quark que produz um barião branco é o RGB. Identifique todas as combinações de cores que podem produzir um méson branco.
65. (a) Três quarks formam um barião. Quantas combinações dos seis quarks conhecidos existem se todas as combinações forem possíveis?
(b) Esse número é menor que o número de bárions conhecidos. Explique o porquê.
Solução
(a) 216
(b) Há mais bárions observados porque também temos os 6 antiquarks e várias misturas de quarks (como no méson π).
66. (a) Mostre que a decomposição conjecturada do próton,\(\displaystyle p→π^0+e^+\), viola a conservação do número de bárions e a conservação do número de léptons.
(b) Qual é o processo de decaimento análogo do antipróton?
67. Verifique os números quânticos dados para o\(\displaystyle Ω^+\) em [link] adicionando os números quânticos de seus constituintes de quarks, conforme inferido na Tabela.
Solução
\(\displaystyle Ω+(\bar{s}\bar{s}\bar{s})\)
\(\displaystyle B=−\frac{1}{3}−\frac{1}{3}−\frac{1}{3}=−1,\)
\(\displaystyle L_e,μ,τ=0+0+0=0,\)
\(\displaystyle Q=\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=1,\)
\(\displaystyle S=1+1+1=3.\)
68. Verifique os números quânticos fornecidos para o próton e o nêutron em [link] adicionando os números quânticos de seus constituintes de quarks, conforme indicado na Tabela.
69. (a) Quanta energia seria liberada se o próton decaísse por meio da reação conjecturada\(\displaystyle p→π^0+e^+\)?
(b) Dado que o\(\displaystyle π^0\) decai para dois\(\displaystyle γ\) s e que o\(\displaystyle e^+\) encontrará um elétron para aniquilar, que energia total é finalmente produzida no decaimento de prótons?
(c) Por que essa energia é maior do que a massa total do próton (convertida em energia)?
Solução
(a) 803 MeV
(b) 938,8 MeV
(c) A energia de aniquilação de um elétron extra está incluída na energia total.
70. (a) Encontre a carga, o número bariônico, a estranheza, o charme e o fundo da\(\displaystyle J/Ψ\) partícula a partir de sua composição de quarks.
(b) Faça o mesmo com a partícula.
71. Existem partículas chamadas de mésons D. Um deles é o\(\displaystyle D^+\) méson, que tem uma única carga positiva e um número bariônico de zero, também o valor de sua estranheza, superfície e fundo. Tem um charme de\(\displaystyle +1\). Qual é sua configuração de quark?
Solução
\(\displaystyle c\bar{d}\)
72. Existem partículas chamadas mésons inferiores ou mésons B. Um deles é o\(\displaystyle B^−\) méson, que tem uma única carga negativa; seu número bariônico é zero, assim como sua estranheza, charme e maciez. Tem um fundo de\(\displaystyle −1\). Qual é sua configuração de quark?
73. (a) Qual partícula tem a composição do quark\(\displaystyle \bar{u}\bar{u}\bar{d}\)?
(b) Qual deveria ser seu modo de decaimento?
Solução
a) O antipróton
b)\(\displaystyle p^−→π^0+e^−\)
74. (a) Mostre que todas as combinações de três quarks produzem cargas integrais. Assim, os bárions devem ter carga integral.
(b) Mostre que todas as combinações de um quark e um antiquark produzem apenas cargas integrais. Assim, os mésons devem ter carga integral.
33.6: Grandes Teorias Unificadas
75. Conceitos integrados
A intensidade da radiação dos raios cósmicos diminui rapidamente com o aumento da energia, mas ocasionalmente existem raios cósmicos extremamente energéticos que criam uma chuva de radiação de todas as partículas que eles criam ao atingir um núcleo na atmosfera, conforme visto na figura abaixo. Suponha que uma partícula de raio cósmico com uma energia de\(\displaystyle 10^{10}GeV\) converta sua energia em partículas com massas médias\(\displaystyle 200MeV/c^2\).
(a) Quantas partículas são criadas?
(b) Se as partículas caírem em uma\(\displaystyle 1.00-km^2\) área, quantas partículas existem por metro quadrado?
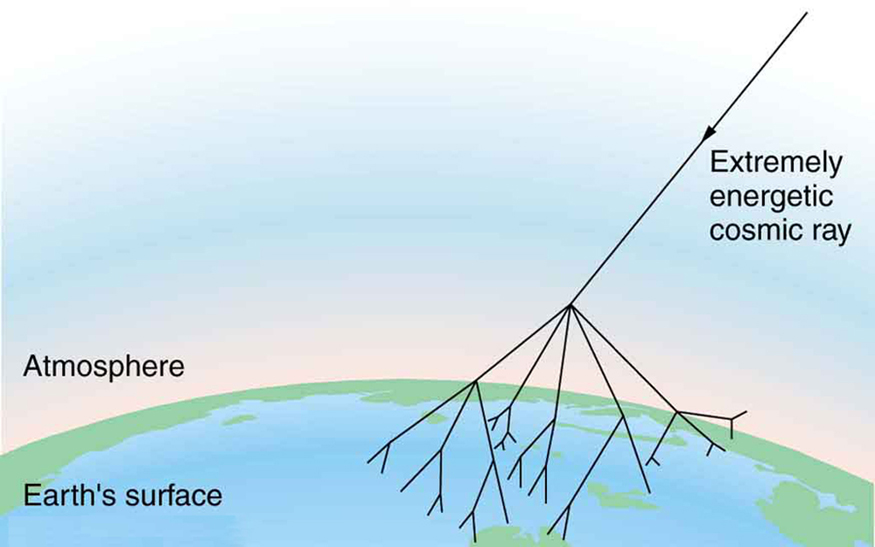
Um raio cósmico extremamente energético cria uma chuva de partículas na Terra. A energia desses raros raios cósmicos pode se aproximar de um joule (cerca de\(\displaystyle 10^{10}GeV\)) e, após várias colisões, um grande número de partículas é criado a partir dessa energia. Observou-se que chuvas de raios cósmicos se estendem por muitos quilômetros quadrados.
Solução
(a)\(\displaystyle 5×10^{10}\)
(b)\(\displaystyle 5×10^4particles/m^2\)
76. Conceitos integrados
Assumindo a conservação do momento, qual é a energia de cada raio γ produzida na decomposição de um píon neutro em repouso, na reação\(\displaystyle π^0→γ+γ\)?
77. Conceitos integrados
Qual é o comprimento de onda de um elétron de 50 GeV, que é produzido no SLAC? Isso fornece uma ideia do limite de detalhes que ele pode sondar.
Solução
\(\displaystyle 2.5×10^{−17}m\)
78. Conceitos integrados
(a) Calcule a quantidade\(\displaystyle γ=\frac{1}{\sqrt{1−v^2/c^2}}\) relativística dos prótons de 1,00-TeV produzidos no Fermilab.
(b) Se tal próton criasse um\(\displaystyle π^+\) com a mesma velocidade, quanto tempo duraria sua vida em laboratório?
(c) Até onde ele poderia viajar nesse período?
79. Conceitos integrados
O modo de decaimento primário para o píon negativo é\(\displaystyle π^−→μ^−+\bar{ν_μ}\).
(a) Qual é a liberação de energia em MeV nesse decaimento?
(b) Usando a conservação do momento, quanta energia cada um dos produtos de decaimento recebe, dado que\(\displaystyle π^−\) está em repouso quando se decompõe? Você pode supor que o múon antineutrino não tem massa e tem impulso\(\displaystyle p=E/c\), assim como um fóton.
Solução
(a) 33,9 MeV
(b) Antineutrino de múon 29,8 MeV, múon 4,1 MeV (energia cinética)
80. Conceitos integrados
Os planos para um acelerador que produz um feixe secundário de mésons K para se dispersar dos núcleos, com o objetivo de estudar a força forte, exigem que eles tenham uma energia cinética de 500 MeV.
(a) Qual seria a quantidade\(\displaystyle γ=\frac{1}{\sqrt{1−v^2/c^2}}\) relativista dessas partículas?
(b) Quanto tempo duraria sua vida útil média no laboratório?
(c) Até onde eles poderiam viajar nesse período?
81. Conceitos integrados
Suponha que você esteja projetando um experimento de decaimento de prótons e possa detectar 50 por cento dos decaimentos de prótons em um tanque de água.
(a) Quantos quilos de água você precisaria para ver um decaimento por mês, supondo uma vida útil de\(\displaystyle 10^{31}y\)?
(b) Quantos metros cúbicos de água são esses?
(c) Se a vida útil real for\(\displaystyle 10^{33}y\), quanto tempo você teria que esperar em média para ver um único próton decair?
Solução
(a)\(\displaystyle 7.2×10^5kg\)
(b)\(\displaystyle 7.2×10^2m^3\)
(c) 100 meses
82. Conceitos integrados
Nas supernovas, os neutrinos são produzidos em grandes quantidades. Eles foram detectados a partir da supernova 1987A na Nuvem de Magalhães, que fica a cerca de 120.000 anos-luz de distância da Terra (relativamente perto da nossa galáxia Via Láctea). Se os neutrinos tiverem uma massa, eles não podem viajar à velocidade da luz, mas se sua massa for pequena, eles podem se aproximar.
(a) Suponha que um neutrino com uma\(\displaystyle 7-eV/c^2\) massa tenha uma energia cinética de 700 keV. Encontre a quantidade relativista\(\displaystyle γ=\frac{1}{\sqrt{1−v^2/c^2}}\) para isso.
(b) Se o neutrino deixar a supernova 1987A ao mesmo tempo que um fóton e ambos viajarem para a Terra, quanto antes o fóton chegará? Essa não é uma grande diferença de tempo, já que é impossível saber qual neutrino ficou com qual fóton e a baixa eficiência dos detectores de neutrinos. Assim, o fato de os neutrinos terem sido observados poucas horas após o brilho da supernova só coloca um limite superior na massa do neutrino. (Dica: talvez seja necessário usar uma expansão em série para encontrar v para o neutrino, já que seu γ é muito grande.)
83. Construa seu próprio problema
Considere um raio cósmico de energia ultra-alta entrando na atmosfera da Terra (alguns têm energias próximas de um joule). Crie um problema no qual você calcule a energia da partícula com base no número de partículas em uma chuva de raios cósmicos observada. Entre as coisas a considerar estão a massa média das partículas do chuveiro, o número médio por metro quadrado e a extensão (número de metros quadrados cobertos) do chuveiro. Expresse a energia em eV e joules.
84. Construa seu próprio problema
Considere um detector necessário para observar o decaimento proposto, mas extremamente raro, de um elétron. Crie um problema no qual você calcule a quantidade de matéria necessária no detector para poder observar a deterioração, assumindo que ele tenha uma assinatura claramente identificável. Entre as coisas a considerar estão a meia-vida estimada (longa para eventos raros) e o número de decaimentos por unidade de tempo que você deseja observar, bem como o número de elétrons na substância detectora.

