33.5: Quarks - Isso é tudo o que existe?

Objetivos de

Ao final desta seção, você poderá:

• Defina a partícula fundamental.
• Descreva quark e antiquark.
• Liste os sabores do quark.
• Descreva a composição dos hádrons em quarks.
• Determine os números quânticos a partir da composição dos quarks.

Os quarks foram mencionados em vários pontos deste texto como blocos de construção fundamentais e membros do clube exclusivo de partículas verdadeiramente elementares. Observe que uma partícula elementar ou fundamental não tem subestrutura (não é feita de outras partículas) e não tem tamanho finito além de seu comprimento de onda. Isso não significa que as partículas fundamentais sejam estáveis — algumas decaem, enquanto outras não. Lembre-se de que todos os léptons parecem ser fundamentais, enquanto nenhum hádron é fundamental. Há fortes evidências de que os quarks são os blocos de construção fundamentais dos hádrons, conforme visto na Figura\(\PageIndex{1}\). Os quarks são o segundo grupo de partículas fundamentais (os léptons são os primeiros). O terceiro e talvez último grupo de partículas fundamentais são as partículas transportadoras das quatro forças básicas. Léptons, quarks e partículas transportadoras podem ser tudo o que existe. Neste módulo, discutiremos a subestrutura de quarks dos hádrons e sua relação com as forças, bem como indicaremos algumas questões e problemas restantes.

Figura\(\PageIndex{1}\): Todos os bárions, como o próton e o nêutron mostrados aqui, são compostos por três quarks. Todos os mésons, como os píons mostrados aqui, são compostos por um par quark-antiquark. As setas representam os giros dos quarks, que, como veremos, também são coloridos. As cores são tais que precisam ser adicionadas ao branco para qualquer combinação possível de quarks.

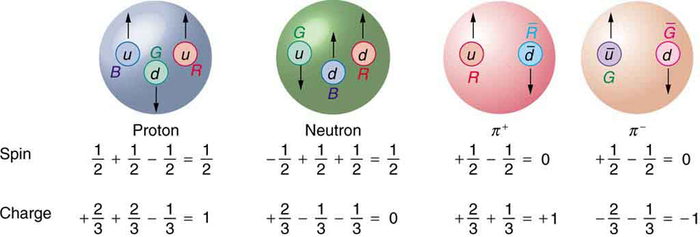
Concepção de Quarks

Os quarks foram propostos pela primeira vez de forma independente pelos físicos americanos Murray Gell-Mann e George Zweig em 1963. Seu nome pitoresco foi tirado por Gell-Mann de um romance de James Joyce — Gell-mann também foi o grande responsável pelo conceito e nome de estranheza. (Nomes extravagantes são comuns na física de partículas, refletindo as personalidades dos físicos modernos.) Originalmente, três tipos de quarks - ou sabores - foram propostos para explicar os mésons e bárions então conhecidos. Esses sabores de quark são chamados de up (\(u\)), down (\(d\)) e strange (\(s\)). Todos os quarks têm spin semi-integral e, portanto, são férmions. Todos os mésons têm spin integral, enquanto todos os bárions têm spin semi-integral. Portanto, os mésons devem ser compostos por um número par de quarks, enquanto os bárions precisam ser compostos por um número ímpar de quarks. A figura\(\PageIndex{1}\) mostra a subestrutura de quarks do próton, nêutron e dois píons. A proposta mais radical de Gell-Mann e Zweig são as cargas fracionárias dos quarks, que são\(±(\frac{2}{3})q_e\) e\((\frac{1}{3})q_e\), enquanto todas as partículas observadas diretamente têm cargas que são múltiplos integrais de qe. Observe que o valor fracionário do quark não viola o fato de que e é a menor unidade de carga observada, porque um quark livre não pode existir. A tabela\(\PageIndex{1}\) lista as características dos seis sabores de quark que agora se acredita existirem. As descobertas feitas desde 1963 exigiram sabores extras de quark, que são divididos em três famílias bastante análogas aos léptons.

Tabela\(\PageIndex{1}\): Quarks e Antiquarks

Nome	Símbolo	Antipartícula	Girar	Cobrança	B	S	c	b	t	Missa\((GeV/c^2)\)
Para cima	u	\(\bar{u}\)	1/2	\(±\frac{2}{3}q_e\)	\(±\frac{1}{3}\)	0	0	0	0	\ ((Gev/c^2)\)” style="alinhamento vertical: médio; ">0,005
Para baixo	d	\(\bar{d}\)	1/2	\(±\frac{1}{3}q_e\)	\(±\frac{1}{3}\)	0	0	0	0	\ ((Gev/c^2)\)” style="alinhamento vertical: médio; ">0,008
Estranho	s	\(\bar{s}\)	1/2	\(±\frac{1}{3}q_e\)	\(±\frac{1}{3}\)	\(±1\)	0	0	0	\ ((Gev/c^2)\)” style="alinhamento vertical: médio; ">0,50
Encantado	c	\(\bar{c}\)	1/2	\(±\frac{2}{3}q_e\)	\(±\frac{1}{3}\)	0	\(±1\)	0	0	\ ((Gev/c^2)\)” style="alinhamento vertical: médio; ">1,6
Parte inferior	b	\(\bar{b}\)	1/2	\(±\frac{1}{3}q_e\)	\(±\frac{1}{3}\)	0	0	\(±1\)	0	\ ((Gev/c^2)\)” style="alinhamento vertical: médio; ">5
Topo	t	\(\bar{t}\)	1/2	\(±\frac{2}{3}q_e\)	\(±\frac{1}{3}\)	0	0	0	\(±1\)	\ ((Gev/c^2)\)” style="alinhamento vertical: médio; ">173

Como isso funciona?

Para entender como essas subestruturas de quarks funcionam, vamos examinar especificamente o próton, o nêutron e os dois píons mostrados na Figura\(\PageIndex{1}\) antes de passar para considerações mais gerais. Primeiro, o próton p é composto pelos três quarks uud, de modo que sua carga total é

\[+\left(\frac{2}{3}\right)q_e+\left(\frac{2}{3}\right)q_e−\left(\frac{1}{3}\right)q_e=q_e\]

como esperado. Com os spins alinhados como na figura, o spin intrínseco do próton é

\[+\left(\dfrac{1}{2}\right)+\left(\dfrac{1}{2}\right)−\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2}\right)\]

também conforme o esperado. Observe que os spins dos quarks ascendentes estão alinhados, de forma que eles estariam no mesmo estado, exceto pelo fato de terem cores diferentes (outro número quântico a ser elaborado um pouco mais tarde). Os quarks obedecem ao princípio de exclusão de Pauli. Comentários semelhantes se aplicam ao nêutron n, que é composto pelos três quarks\(udd\). Observe também que o nêutron é feito de cargas que somam zero, mas se movem internamente, produzindo seu conhecido momento magnético. Quando o nêutron\(β^−\) decai, ele faz isso alterando o sabor de um de seus quarks. Escrevendo o\(β^−\) decaimento de nêutrons em termos de quarks,

\[n→p+β^−+\bar{v_e}\]

torna-se

\[udd→uud+β^−+\bar{v_e}\]

Vemos que isso equivale a um down quark mudar de sabor para se tornar um up quark:

\[d→u+β^−+\bar{v_e}\]Este é um exemplo do fato geral de que a fraca força nuclear pode mudar o sabor de um quark. Em geral, queremos dizer que qualquer quark pode ser convertido em qualquer outro (mudar o sabor) pela fraca força nuclear. Não só podemos obter\(d→u\), mas também podemos obter\(u→d\). Além disso, o quark estranho também pode ser alterado pela força fraca, tornando\(s→u\)\(s→d\) possível. Isso explica a violação da conservação da estranheza pela força fraca observada na seção anterior. Outro fato geral é que a forte força nuclear não pode mudar o sabor de um quark.

Novamente,\(π^+\) na Figura\(\PageIndex{1}\), vemos que o méson (um dos três pions) é composto por um quark up mais um quark antidown, ou\(u\bar{d}\). Sua carga total é\(+(\frac{2}{3})q_e+(\frac{1}{3})q_e=q_e\), portanto, a esperada. Seu número bariônico é 0, pois tem um quark e um antiquark com números bariônicos\(+(\frac{1}{3})−(\frac{1}{3})=0\). A\(π^+\) meia-vida é relativamente longa, pois, embora seja composto de matéria e antimatéria, os quarks têm sabores diferentes e a força fraca deve causar a decomposição ao mudar o sabor de um para o do outro. Os spins dos\(\bar{d}\) quarks\(u\) e são antiparalelos, permitindo que o píon tenha spin zero, conforme observado experimentalmente. Finalmente, o\(π^−\) méson mostrado na Figura\(\PageIndex{1}\) é a antipartícula do\(π^+\) méson e é composto pelas antipartículas de quark correspondentes. Ou seja, o\(π^+\) méson é\(u\bar{d}\), enquanto o\(π^−\) méson é\(u\bar{d}\). Esses dois píons se aniquilam rapidamente, porque seus quarks constituintes são as antipartículas um do outro.

Regras do Quark

Duas regras gerais para combinar quarks para formar hádrons são:

1. Os bárions são compostos por três quarks e os antibárions são compostos por três antiquarks.
2. Os mésons são combinações de um quark e um antiquark.

Uma das coisas inteligentes sobre esse esquema é que apenas cargas integrais resultam, mesmo que os quarks tenham carga fracionária.

Todas as combinações são possíveis

Todas as combinações de quarks são possíveis e a Tabela\(\PageIndex{2}\) lista algumas dessas combinações. Quando Gell-Mann e Zweig propuseram os três sabores originais de quark, partículas correspondentes a todas as combinações desses três não haviam sido observadas. O padrão estava lá, mas estava incompleto, como aconteceu na tabela periódica dos elementos e no gráfico dos nuclídeos. A\(Ω^−\) partícula, em particular, não havia sido descoberta, mas foi prevista pela teoria dos quarks. Sua combinação de três quarks estranhos,\(sss\), confere-lhe uma estranheza\(−3\) e outras características previsíveis, como rotação, carga, massa aproximada e vida útil. Se a imagem do quark estiver completa, ela\(Ω^−\) deve existir. Foi observado pela primeira vez em 1964 no Laboratório Nacional de Brookhaven e tinha as características previstas, conforme visto na Figura\(\PageIndex{2}\). A descoberta do\(Ω^−\) foi uma evidência indireta convincente da existência dos três sabores originais de quark e impulsionou os esforços teóricos e experimentais para explorar ainda mais a física de partículas em termos de quarks.

Tabela\(\PageIndex{2}\): Composição de quarks de hádrons selecionados

Partícula	Composição do Quark	Partícula	Composição do Quark
Mésons		Bárions
\(π^+\)	\(u\bar{d}\)	\(p\)	\(uud\)
\(π^−\)	\(\bar{u}d\)	\(n\)	\(udd\)
\(π^0\), mistura	\(u\bar{u}\) \(d\bar{d}\)	\(Δ^0\)	\(udd\)
\(η^0\), mistura	\(u\bar{u}\) \(d\bar{d}\)	\(Δ^+\)	\(uud\)
\(K^0\)	\(d\bar{s}\)	\(Δ^−\)	\(ddd\)
\(\bar{K}^0\)	\(\bar{d}s\)	\(Δ^{++}\)	\(uuu\)
\(K^+\)	\(u\bar{s}\)	\(Λ^0\)	\(uds\)
\(K^−\)	\(\bar{u}s\)	\(Σ^0\)	\(uds\)
\(J/ψ\)	\(c\bar{c}\)	\(Σ^+\)	\(uus\)
\(ϒ\)	\(b\bar{b}\)	\(Σ^−\)	\(dds\)
		\(Ξ^0\)	\(uss\)
		\(Ξ^−\)	\(dss\)
		\(Ω^−\)	\(sss\)

PADRÕES E QUEBRA-CABEÇAS: ÁTOMOS, NÚCLEOS E QUARKS

Os padrões nas propriedades dos átomos permitiram que a tabela periódica fosse desenvolvida. A partir disso, elementos até então desconhecidos foram previstos e observados. Da mesma forma, padrões foram observados nas propriedades dos núcleos, levando ao gráfico de nuclídeos e previsões bem-sucedidas de nuclídeos até então desconhecidos. Agora, com a física de partículas, os padrões implicam em uma subestrutura de quarks que, se interpretada literalmente, prevê partículas até então desconhecidas. Eles agora foram observados em outro triunfo da unidade subjacente.

Figura\(\PageIndex{2}\): A imagem está relacionada à descoberta do\(Ω^−\). É uma reação secundária na qual um acelerador produzido\(K^−\) colide com um próton por meio da força forte e conserva a estranheza para produzir as\(Ω^−\) características previstas pelo modelo de quarks. Como em outras previsões de partículas não observadas anteriormente, isso deu um grande impulso à teoria dos quarks. (crédito: Laboratório Nacional de Brookhaven)

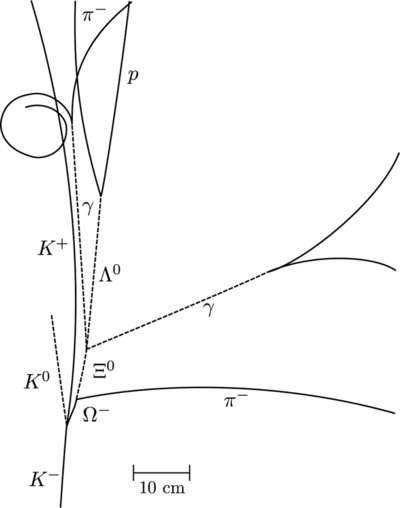
Exemplo\(\PageIndex{1}\): Quantum Numbers From Quark Composition

Verifique os números quânticos fornecidos para a\(Ξ^0\) partícula adicionando os números quânticos para sua composição de quarks, conforme indicado na Tabela\(\PageIndex{2}\).

Estratégia

A composição do\(Ξ^0\) é dada como\(uss\) na Tabela\(\PageIndex{2}\). Os números quânticos dos quarks constituintes são dados na Tabela\(\PageIndex{1}\). Não consideraremos a rotação, porque isso não é dado para\(Ξ^0\) o. Mas podemos verificar a carga e os outros números quânticos dados para os quarks.

Solução

A carga total de\(uss\) é\(+(\frac{2}{3})q_e−(\frac{1}{3})q_e−(\frac{1}{3})q_e=0\), o que é correto para\(Ξ^0\) o. O número bariônico também está correto\(+(\frac{1}{3})+(\frac{1}{3})+(\frac{1}{3})=1\), pois o\(Ξ^0\) é uma matéria bariônica e tem\(B=1\), conforme listado em [link]. Sua estranheza é\(S=0−1−1=−2\), também, a esperada de [link]. Seu charme, fundo e altura são 0, assim como os números da família leptônica (não é um lépton).

Discussão

Esse procedimento é semelhante ao que os inventores da hipótese dos quarks fizeram ao verificar se a solução para o quebra-cabeça dos padrões de partículas estava correta. Eles também verificaram se todas as combinações eram conhecidas, prevendo assim o não observado anteriormente\(Ω^−\) como a conclusão de um padrão.

Agora, vamos falar sobre evidências diretas

A princípio, os físicos esperavam que, com energia suficiente, pudéssemos liberar quarks e observá-los diretamente. Isso não provou ser possível. Ainda não há observação direta de uma carga fracionária ou de qualquer quark isolado. Quando grandes energias são colocadas em colisões, outras partículas são criadas, mas nenhum quark surge. Há evidências quase diretas de quarks que são bastante convincentes. Em 1967, experimentos no SLAC espalhando elétrons de 20 GeV de prótons produziram resultados como Rutherford havia obtido para o núcleo quase 60 anos antes. Os experimentos de espalhamento do SLAC mostraram inequivocamente que havia três cargas pontuais (o que significa que tinham tamanhos consideravelmente menores que o comprimento de onda da sonda) dentro do próton, conforme visto na Figura\(\PageIndex{3}\). Essa evidência fez com que todos, exceto os mais céticos, admitissem que havia validade na subestrutura de quarks dos hádrons.

Figura\(\PageIndex{3}\): A dispersão de elétrons de alta energia de prótons em instalações como o SLAC produz evidências de cargas semelhantes a três pontos consistentes com as propriedades de quarks propostas. Esse experimento é análogo à descoberta de Rutherford do tamanho pequeno do núcleo ao espalhar partículas α. Elétrons de alta energia são usados para que o comprimento de onda da sonda seja pequeno o suficiente para ver detalhes menores que o próton.

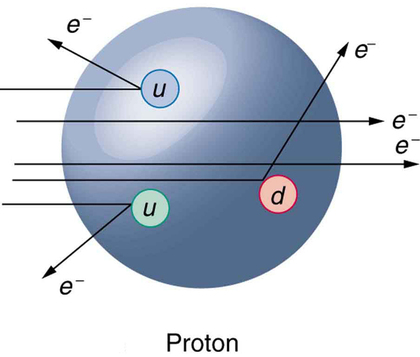
Experimentos mais recentes e de alta energia produziram jatos de partículas em colisões, altamente sugestivos de três quarks em um nucleon. Como os quarks estão muito estreitamente ligados, a energia usada para separá-los os afasta apenas até certo ponto antes de começar a ser convertida em outras partículas. Mais energia produz mais partículas, não uma separação de quarks. A conservação do momento exige que as partículas saiam em jatos ao longo dos três caminhos pelos quais os quarks estavam sendo puxados. Observe que existem apenas três jatos e que outras características das partículas são consistentes com a subestrutura de três quarks.

Figura\(\PageIndex{4}\): Simulação de uma colisão próton-próton na energia do centro de massa de 14 TeV no detector ALICE no CERN LHC. As linhas seguem as trajetórias das partículas e os pontos ciano representam as deposições de energia nos elementos sensíveis do detector. (crédito: Matevž Tadel)

Os quarks têm seus altos e baixos

Na verdade, o modelo quark perdeu parte de sua popularidade inicial porque o modelo original com três quarks teve que ser modificado. Os quarks para cima e para baixo pareciam compor a matéria normal, conforme visto na Tabela\(\PageIndex{1}\), enquanto o único quark estranho explicava a estranheza. Por que não tinha uma contrapartida? Um quarto sabor de quark chamado charme (c) foi proposto como a contrapartida do quark estranho para tornar as coisas simétricas — haveria dois quarks normais (u e d) e dois quarks exóticos (s e c). Além disso, naquela época eram conhecidos apenas quatro léptons, dois normais e dois exóticos. Era atraente que houvesse quatro quarks e quatro léptons. O problema era que nenhuma partícula conhecida continha um quark encantado. De repente, em novembro de 1974, dois grupos (um liderado por C. C. Ting no Laboratório Nacional de Brookhaven e outro por Burton Richter no SLAC) descobriram de forma independente e quase simultaneamente um novo méson com características que deixaram claro que sua subestrutura é\(c\bar{c}\). Foi chamado\(J\) por um grupo e psi (\(ψ\)) pelo outro e agora é conhecido como\(J/ψ\) méson. Desde então, várias partículas foram descobertas contendo o quark encantado, consistente em todos os sentidos com o modelo quark. A descoberta do\(J/ψ\) méson teve um efeito tão rejuvenescedor na teoria dos quarks que agora é chamada de Revolução de Novembro. Ting e Richter dividiram o Prêmio Nobel de 1976.

A história rapidamente se repetiu. Em 1975, o tau (\(τ\)) foi descoberto e uma terceira família de léptons surgiu, como visto em [link]). Os teóricos rapidamente propuseram mais dois sabores de quarks chamados top (\(t\)) ou truth and bottom (\(b\)) ou beauty para manter o número de quarks igual ao número de léptons. E em 1976, o méson upsilon (\(Υ\)) foi descoberto e demonstrou ser composto por um quark inferior e um antibottom ou\(b\bar{b}\), bastante análogo ao\(J/ψ\) ser,\(c\bar{c}\) conforme visto na Tabela\(\PageIndex{2}\). Sendo um sabor único, esses mésons às vezes são chamados de charme nu e fundo nu e revelam as características de seus quarks com mais clareza. Outros mésons contendo quarks inferiores já foram observados. Em 1995, dois grupos no Fermilab confirmaram a existência do quark superior, completando o quadro de seis quarks listados na Tabela\(\PageIndex{1}\). Cada descoberta sucessiva de quarks — primeiro\(c\)\(b\), depois e finalmente\(t\) — exigiu maior energia porque cada uma tem maior massa. As massas de quarks na Tabela\(\PageIndex{1}\) são conhecidas apenas aproximadamente, porque não são observadas diretamente. Eles devem ser inferidos a partir das massas das partículas que combinam para formar.

O que a cor tem a ver com isso? —Um tom mais branco de pálido

Conforme mencionado e mostrado na Figura\(\PageIndex{1}\), os quarks carregam outro número quântico, que chamamos de cor. Obviamente, não é a cor que sentimos com a luz visível, mas suas propriedades são análogas às de três cores primárias e três secundárias. Especificamente, um quark pode ter um dos três valores de cor que chamamos de vermelho (\(R\)), verde (\(G\)) e azul (\(B\)) em analogia com essas cores primárias visíveis. Os antiquarks têm três valores que chamamos de antivermelho ou ciano (\(\bar{R}\)), antiverde ou magenta (\(\bar{G}\)) e antiazul ou amarelo (\(\bar{B}\)) em analogia com essas cores visíveis secundárias. A razão para esses nomes é que, quando certas cores visuais são combinadas, o olho vê o branco. A analogia das cores combinadas com o branco é usada para explicar por que os bárions são feitos de três quarks, por que os mésons são um quark e um antiquark e por que não podemos isolar um único quark. A força entre os quarks é tal que suas cores combinadas produzem branco. Isso é ilustrado na Figura\(\PageIndex{5}\). Um bárion deve ter uma de cada cor primária ou RGB, que produz branco. Um méson deve ter uma cor primária e sua anticor, produzindo também o branco.

Figura\(\PageIndex{5}\): Os três quarks que compõem um barião devem ser RGB, que se somam ao branco. O quark e o antiquark que compõem um méson devem ser coloridos e anticoloridos, aqui\(R\bar{R}\) também aumentando o branco. A força entre sistemas que têm cores é tão grande que eles não podem ser separados nem existir como coloridos.

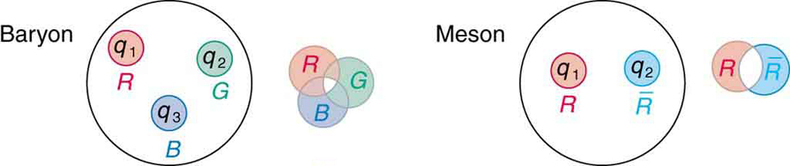
Por que os hádrons devem ser brancos? O esquema de cores foi criado intencionalmente para explicar por que os bárions têm três quarks e os mésons têm um quark e um antiquark. Acredita-se que a cor do quark seja semelhante à carga, mas com mais valores. Um íon, por analogia, exerce forças muito mais fortes do que uma molécula neutra. Quando a cor de uma combinação de quarks é branca, é como um átomo neutro. As forças que uma partícula branca exerce são como as forças de polarização nas moléculas, mas nos hádrons essas sobras são a força nuclear forte. Quando uma combinação de quarks tem uma cor diferente do branco, ela exerce forças extremamente grandes — ainda maiores que a força forte — e talvez não possa ser estável ou separada permanentemente. Isso faz parte da teoria do confinamento de quarks, que explica como os quarks podem existir e, ainda assim, nunca serem isolados ou observados diretamente. Finalmente, um número quântico extra com três valores (como aqueles que atribuímos à cor) é necessário para que os quarks obedeçam ao princípio de exclusão de Pauli. Partículas como o\(Ω^−\), que é composto por três quarks estranhos,\(sss\), e o\(Δ^{++}\), que é três quarks ascendentes, uuu, podem existir porque os quarks têm cores diferentes e não têm os mesmos números quânticos. A cor é consistente com todas as observações e agora é amplamente aceita. A teoria dos quarks, incluindo a cor, é chamada de cromodinâmica quântica (QCD), também chamada por Gell-Mann.

As três famílias de partículas fundamentais

Acredita-se que as partículas fundamentais sejam um dos três tipos: léptons, quarks ou partículas transportadoras. Cada um desses três tipos é dividido em três famílias análogas, conforme ilustrado na Figura\(\PageIndex{6}\). Examinamos léptons e quarks com alguns detalhes. Cada um tem seis membros (e suas seis antipartículas) divididos em três famílias análogas. A primeira família é a matéria normal, da qual a maioria das coisas são compostas. O segundo é exótico e o terceiro mais exótico e mais massivo que o segundo. As únicas partículas estáveis estão na primeira família, que também tem membros instáveis.

Figura\(\PageIndex{6}\): Os três tipos de partículas são léptons, quarks e partículas transportadoras. Cada um desses tipos é dividido em três famílias análogas, com o graviton deixado de fora.

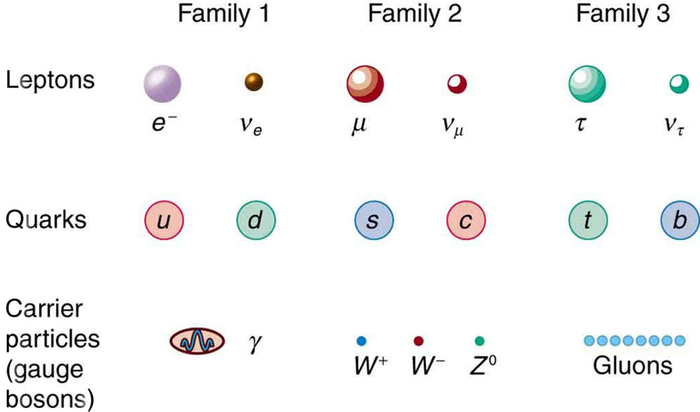
Sempre em busca de simetria e semelhança, os físicos também dividiram as partículas transportadoras em três famílias, omitindo o gráviton. A gravidade é especial entre as quatro forças, pois afeta o espaço e o tempo em que as outras forças existem e está se mostrando mais difícil de incluir em uma Teoria de Tudo ou TOE (para acabar com a pretensão de tal teoria). A gravidade é, portanto, frequentemente separada. Não é certo que haja significado nos agrupamentos mostrados na Figura, mas as analogias são tentadoras. No passado, conseguimos fazer avanços significativos procurando analogias e padrões, e este é um exemplo de um que está sob análise atual. Existem conexões entre as famílias de léptons, na medida em que o\(τ\) decai para o\(μ\) e o\(μ\) para o e. Da mesma forma, para os quarks, as famílias superiores eventualmente se decompõem para as mais baixas, deixando apenas os quarks u e d. Há muito tempo buscamos conexões entre as forças da natureza. Como elas são transportadas por partículas, exploraremos as conexões entre glúons\(W^±\) e\(Z^0\) fótons como parte da busca pela unificação de forças discutida em GUTs: A Unificação de Forças.

Resumo

• Acredita-se que os hádrons sejam compostos de quarks, com bárions tendo três quarks e mésons tendo um quark e um antiquark.
• As características dos seis quarks e suas contrapartes antiquarks são apresentadas na Tabela\(\PageIndex{1}\), e as composições de quarks de certos hádrons são apresentadas na Tabela\(\PageIndex{2}\).
• A evidência indireta dos quarks é muito forte, explicando todos os hádrons conhecidos e seus números quânticos, como estranheza, charme, superioridade e fundo.
• Os quarks vêm em seis sabores e três cores e ocorrem apenas em combinações que produzem branco.
• As partículas fundamentais não têm mais subestrutura, nem mesmo um tamanho além do comprimento de onda de Broglie.
• Existem três tipos de partículas fundamentais: léptons, quarks e partículas transportadoras. Cada tipo é dividido em três famílias análogas, conforme indicado na Figura\(\PageIndex{6}\).

Notas de pé

1 O menor dos\(±\) símbolos são os valores dos antiquarks.

2\(B\) é número bariônico,\(S\) é estranheza,\(c\) é charme,\(b\) é fundo,\(t\) é superioridade.

3 Os valores são aproximados, não são diretamente observáveis e variam com o modelo.

4 Esses dois mésons são misturas diferentes, mas cada um é sua própria antipartícula, conforme indicado por sua composição de quarks.

5 Esses dois mésons são misturas diferentes, mas cada um é sua própria antipartícula, conforme indicado por sua composição de quarks.

6 Esses dois mésons são misturas diferentes, mas cada um é sua própria antipartícula, conforme indicado por sua composição de quarks.

7 Antibárions têm os antiquarks de suas contrapartes. O antipróton\(\bar{p}\) é\(\bar{u}\bar{u}d\), por exemplo.

8 bárions compostos pelos mesmos quarks são estados diferentes da mesma partícula. Por exemplo, o\(Δ^+\) é um estado excitado do próton.

Glossário

parte inferior

um sabor de quark

encanto

um sabor de quark, que é a contrapartida do estranho quark

cor

um sabor de quark

para baixo

o segundo mais leve de todos os quarks

sabores

tipo de quark

partícula fundamental

partícula sem subestrutura

cromodinâmica quântica

teoria dos quarks, incluindo cor

quark

uma partícula elementar e um constituinte fundamental da matéria

estranho

o terceiro mais leve de todos os quarks

teoria do confinamento de quarks

explica como os quarks podem existir e, ainda assim, nunca serem isolados ou observados diretamente

topo

um sabor de quark

para cima

o mais leve de todos os quarks