28.5: Momento relativista

Last updated
Save as PDF

Page ID: 194176

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Calcule o momento relativístico.
Explique por que a única massa sobre a qual faz sentido falar é a massa de descanso.

Na física clássica, o momentum é um produto simples de massa e velocidade. No entanto, vimos na última seção que quando a relatividade especial é levada em consideração, objetos massivos têm um limite de velocidade. Que efeito você acha que a massa e a velocidade têm no momento dos objetos se movendo em velocidades relativistas?

Foto de ação de um jogo de futebol americano universitário. — Figura\(\PageIndex{1}\): Momentum é um conceito importante para esses jogadores de futebol da Universidade da Califórnia em Berkeley e da Universidade da Califórnia em Davis. Jogadores com mais massa geralmente têm um impacto maior porque seu impulso é maior. Para objetos que se movem em velocidades relativísticas, o efeito é ainda maior. (crédito: John Martinez Pavliga)

Momentum é um dos conceitos mais importantes da física. A forma mais ampla da segunda lei de Newton é declarada em termos de momentum. O momentum é conservado sempre que a força externa líquida em um sistema é zero. Isso torna a conservação de momentum uma ferramenta fundamental para analisar colisões. Todo o trabalho, energia e recursos energéticos é dedicado ao impulso, e o momentum também tem sido importante para muitos outros tópicos, especialmente quando houve colisões. Veremos que o momentum tem a mesma importância na física moderna. O momento relativístico é conservado, e muito do que sabemos sobre a estrutura subatômica vem da análise de colisões de partículas relativistas produzidas por aceleradores.

O primeiro postulado da relatividade afirma que as leis da física são as mesmas em todos os quadros inerciais. A lei da conservação do momentum sobrevive a essa exigência em altas velocidades? A resposta é sim, desde que o momentum seja definido da seguinte forma.

Definição: Momento relativístico

O momentum relativístico\(p\) é o momento clássico multiplicado pelo fator relativista\(\gamma\)

\[p = \gamma mu,\]

onde\(m\) está a massa restante do objeto,\(u\) sua velocidade em relação a um observador e o fator relativista

\[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{u^2}{c^2}}}.\]

Observe que usamos\(u\) a velocidade aqui para distingui-la da velocidade relativa\(v\) entre observadores. Apenas um observador está sendo considerado aqui. Com\(p\) definido dessa forma, o momento total\(p_{tot}\) é conservado sempre que a força externa líquida é zero, assim como na física clássica. Novamente, vemos que a quantidade relativista se torna virtualmente a mesma que a clássica em baixas velocidades. Ou seja, o momento relativístico\(\gamma mu\) se torna o clássico\(mu\) em baixas velocidades, porque\(\gamma\) é quase igual a 1 em baixas velocidades.

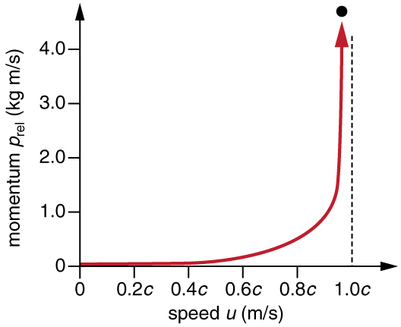
O momentum relativista tem a mesma sensação intuitiva do momentum clássico. É melhor para grandes massas que se movem em altas velocidades, mas, por causa do fator\(\gamma\), o momento relativístico se aproxima do infinito à medida que\(u\) se aproxima\(c\) (Figura\(\PageIndex{2}\)). Essa é outra indicação de que um objeto com massa não pode atingir a velocidade da luz. Se isso acontecesse, seu impulso se tornaria infinito, um valor irracional.

Nesta figura, um gráfico é mostrado em um sistema de coordenadas de eixos. O eixo x é rotulado como velocidade u metro por segundo. No eixo x, a velocidade do objeto é mostrada em termos da velocidade da luz começando de zero na origem até um ponto zero c, onde c é a velocidade da luz. O eixo y é rotulado como momentum p rel quilograma metro por segundo. No eixo y, o momento relativístico é mostrado em termos de quilograma-metro por partida de zero na origem até quatro pontos zero. O gráfico na figura dada é côncavo para cima e mover-se para cima ao longo da linha vertical em x é igual a um ponto zero c. Este gráfico mostra que o momento relativístico se aproxima do infinito quando a velocidade de um objeto se aproxima da velocidade da luz. — Figura\(\PageIndex{2}\): O momento relativístico se aproxima do infinito quando a velocidade de um objeto se aproxima da velocidade da luz.

ALERTA DE EQUÍVOCO: MASSA E IMPULSO RELATIVISTAS

A definição relativisticamente correta de momentum como\(p = \gamma mu\), às vezes implica que a massa varia com a velocidade:\(m_{var} = \gamma m\), particularmente em livros didáticos mais antigos. No entanto, observe que\(m\) é a massa do objeto medida por uma pessoa em repouso em relação ao objeto. Assim,\(m\) é definida como a massa restante, que poderia ser medida em repouso, talvez usando a gravidade. Quando uma massa está se movendo em relação a um observador, a única maneira de determinar sua massa é por meio de colisões ou outros meios nos quais o momento está envolvido. Como a massa de um objeto em movimento não pode ser determinada independentemente do momento, a única massa significativa é a massa restante. Assim, quando usamos o termo massa, suponha que ele seja idêntico à massa restante.

O momento relativístico é definido de tal forma que a conservação do momento se manterá em todos os quadros inerciais. Sempre que a força externa líquida em um sistema é zero, o momento relativístico é conservado, assim como é o caso do momento clássico. Isso foi verificado em vários experimentos.

Na Seção sobre Energia Relativista, a relação do momento relativista com a energia é explorada. Esse assunto produzirá nossa primeira impressão de que objetos sem massa também podem ter impulso.

Exercício\(\PageIndex{1}\)

Qual é o momento de um elétron viajando a uma velocidade\(0.985 c\)? A massa restante do elétron é\(9.11 \times 10^{-31} \, kg\).

Resposta: \[ \begin{align*} p &= \gamma mu \\[5pt] &= \dfrac{mu}{\sqrt{1 - \frac{u^2}{c^2}}} \\[5pt] &= \dfrac{(9.11 \times 10^{-31} kg) (0.985 c)(3.00 \times 10^8 m/s)}{\sqrt{1 - \frac{(0.985 c)2}{c^2}}} \\[5pt] &= 1.56 \times 10^{-21} kg \cdot m/s \end{align*} \]

Resumo

A lei da conservação do momento é válida sempre que a força externa líquida é zero e para o momento relativístico. O momentum relativístico\(p\) é o momento clássico multiplicado pelo fator relativista\(\gamma\)
\(p = \gamma mu\), onde\(m\) está a massa restante do objeto,\(u\) é sua velocidade em relação a um observador e o fator relativista\(\gamma = \frac{1}{\sqrt{1 - \frac{u^2}{c^2}}}.\)
Em baixas velocidades, o momento relativístico é equivalente ao momento clássico.
O momentum relativista se aproxima do infinito como\(u\) se aproxima\(c\). Isso implica que um objeto com massa não pode atingir a velocidade da luz.
O momentum relativista é conservado, assim como o momentum clássico é conservado.

Glossário

momentum relativístico: \(p\), o momento de um objeto se movendo na velocidade relativista;\(p = \gamma mu\), onde\(m\) está a massa restante do objeto,\(u\) é sua velocidade em relação a um observador e o fator relativista\(\gamma = \frac{1}{\sqrt{1 - \frac{u^2}{c^2}}}\)

massa de descanso: a massa de um objeto medida por uma pessoa em repouso em relação ao objeto