27.8: Polarização

Objetivos de

Ao final desta seção, você poderá

• Discuta o significado da polarização.
• Discuta a propriedade da atividade óptica de certos materiais.

Os óculos de sol Polaroid são familiares para a maioria de nós. Eles têm uma habilidade especial de cortar o brilho da luz refletida pela água ou pelo vidro (Figura\(\PageIndex{1}\)). As polaroides têm essa capacidade devido a uma onda característica da luz chamada polarização. O que é polarização? Como é produzido? Quais são alguns de seus usos? As respostas a essas perguntas estão relacionadas ao caráter ondulatório da luz.

Figura\(\PageIndex{1}\): Essas duas fotografias de um rio mostram o efeito de um filtro polarizador na redução do brilho na luz refletida na superfície da água. Parte (b) dessa figura foi tirada com um filtro polarizador e a parte (a) não. Como resultado, o reflexo das nuvens e do céu observado na parte (a) não é observado na parte (b). Óculos de sol polarizados são particularmente úteis na neve e na água. (crédito: Amithshs, Wikimedia Commons)

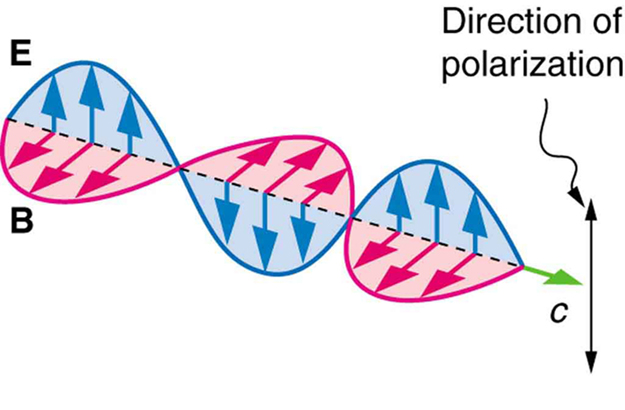
A luz é um tipo de onda eletromagnética (EM). Conforme observado anteriormente, as ondas EM são ondas transversais que consistem em campos elétricos e magnéticos variáveis que oscilam perpendicularmente à direção da propagação (Figura\(\PageIndex{2}\)). Existem direções específicas para as oscilações dos campos elétrico e magnético. A polarização é o atributo de que as oscilações de uma onda têm uma direção definida em relação à direção de propagação da onda. (Esse não é o mesmo tipo de polarização discutido para a separação de cargas.) Diz-se que as ondas com essa direção são polarizadas. Para uma onda EM, definimos a direção da polarização como sendo a direção paralela ao campo elétrico. Assim, podemos pensar nas setas do campo elétrico como mostrando a direção da polarização, como na Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Uma onda EM, como a luz, é uma onda transversal. Os campos elétrico e magnético são perpendiculares à direção da propagação.

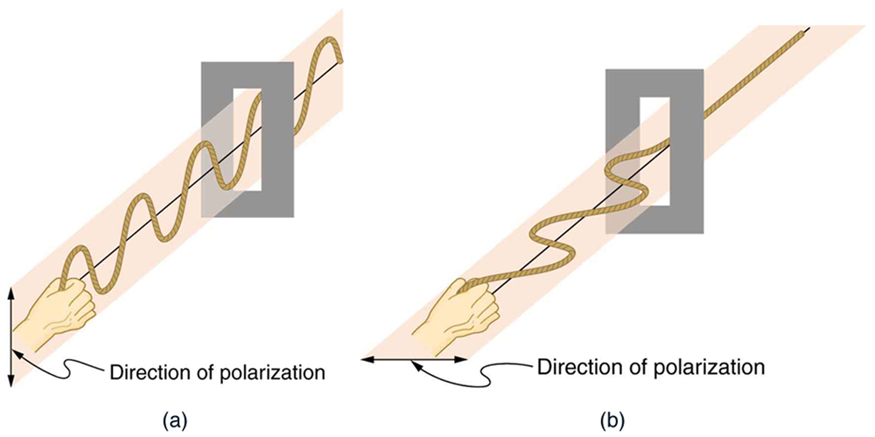
Para examinar isso mais detalhadamente, considere as ondas transversais nas cordas mostradas na Figura\(\PageIndex{3}\). As oscilações em uma corda estão em um plano vertical e dizem que estão polarizadas verticalmente. Os que estão na outra corda estão em um plano horizontal e são polarizados horizontalmente. Se uma fenda vertical for colocada na primeira corda, as ondas passam. No entanto, uma fenda vertical bloqueia as ondas polarizadas horizontalmente. Para ondas EM, a direção do campo elétrico é análoga às perturbações nas cordas.

Figura\(\PageIndex{3}\): As oscilações transversais em uma corda estão em um plano vertical e as da outra corda estão em um plano horizontal. Diz-se que o primeiro é polarizado verticalmente e o outro é polarizado horizontalmente. As fendas verticais passam ondas polarizadas verticalmente e bloqueiam as ondas polarizadas horizontalmente.

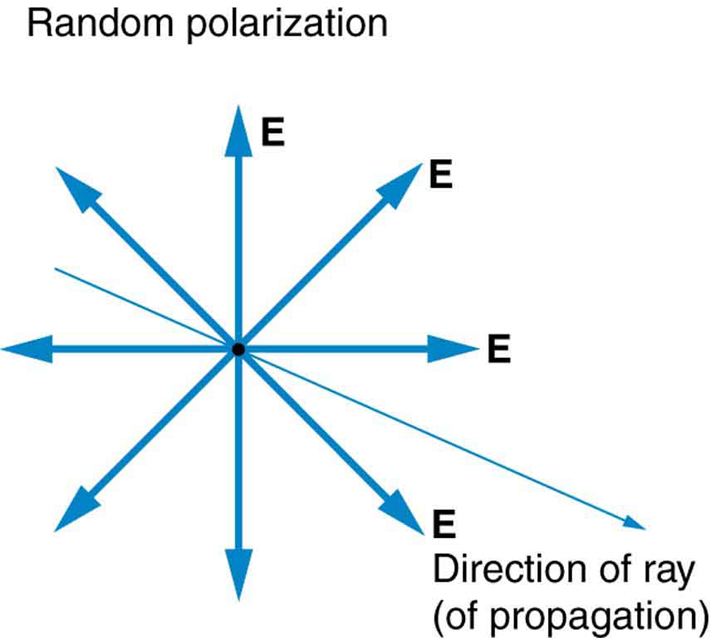
O Sol e muitas outras fontes de luz produzem ondas que são polarizadas aleatoriamente (Figura\(\PageIndex{4}\)). Diz-se que essa luz não é polarizada porque é composta por muitas ondas com todas as direções possíveis de polarização.

Figura\(\PageIndex{4}\): A seta delgada representa um raio de luz não polarizada. As setas em negrito representam a direção da polarização das ondas individuais que compõem o raio. Como a luz não é polarizada, as setas apontam em todas as direções.

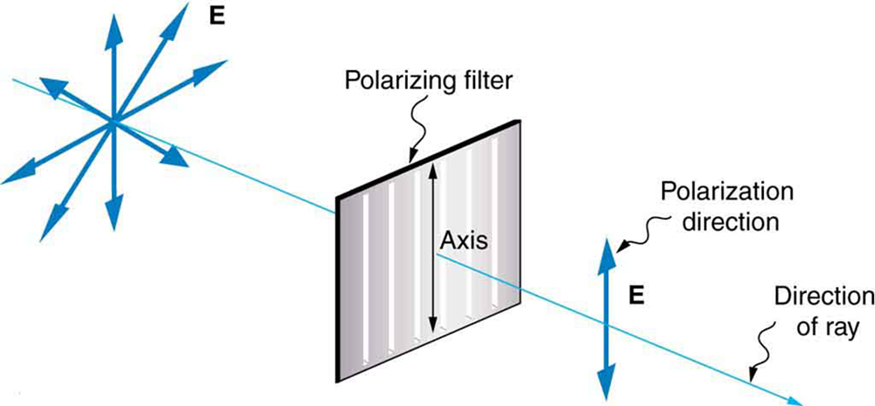
Os materiais Polaroid, inventados pelo fundador da Polaroid Corporation, Edwin Land, atuam como uma fenda polarizadora para a luz, permitindo que apenas a polarização em uma direção passe. Os filtros polarizadores são compostos por moléculas longas alinhadas em uma direção. Pensando nas moléculas como muitas fendas, análogas às das cordas oscilantes, podemos entender por que somente a luz com uma polarização específica pode passar. O eixo de um filtro polarizador é a direção ao longo da qual o filtro passa pelo campo elétrico de uma onda EM (Figura\(\PageIndex{5}\)).

Figura\(\PageIndex{5}\): Um filtro polarizador tem um eixo de polarização que atua como uma fenda passando por campos elétricos paralelos à sua direção. A direção de polarização de uma onda EM é definida como sendo a direção de seu campo elétrico.

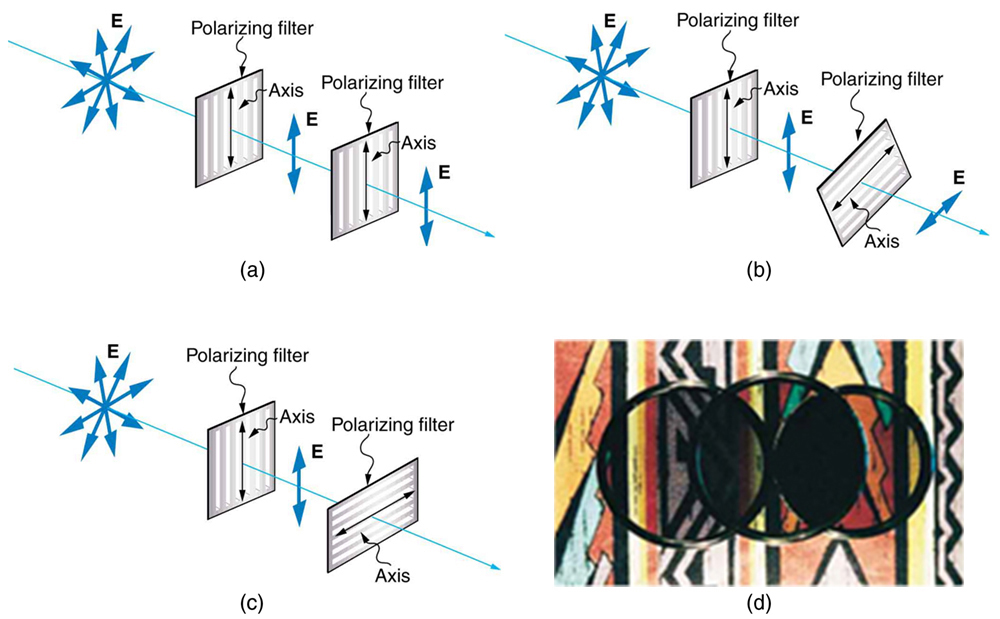
A figura\(\PageIndex{6}\) mostra o efeito de dois filtros polarizadores na luz originalmente não polarizada. O primeiro filtro polariza a luz ao longo de seu eixo. Quando os eixos do primeiro e do segundo filtros estão alinhados (paralelos), toda a luz polarizada passada pelo primeiro filtro também passa pelo segundo. Se o segundo filtro polarizador for girado, somente o componente da luz paralelo ao eixo do segundo filtro será passado. Quando os eixos são perpendiculares, nenhuma luz passa pelo segundo.

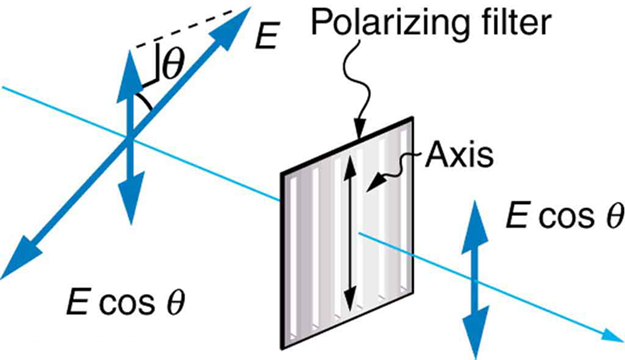
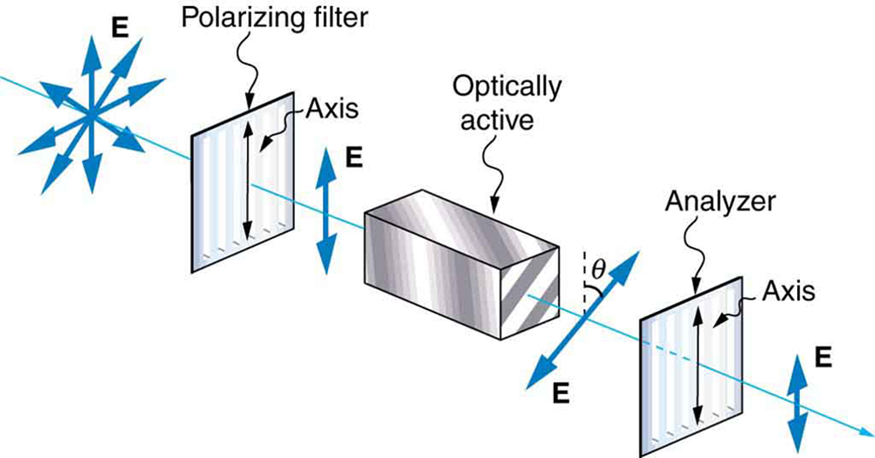
Somente o componente da onda EM paralelo ao eixo de um filtro é passado. Vamos chamar o ângulo entre a direção da polarização e o eixo de um filtro\(\theta\). Se o campo elétrico tiver uma amplitude\(E\), a parte transmitida da onda terá uma amplitude\(E \cos{\theta}\) (Figura\(\PageIndex{7}\)). Como a intensidade de uma onda é proporcional ao quadrado de sua amplitude, a intensidade\(I\) da onda transmitida está relacionada à onda incidente por

\[I = I_{0}\cos{\theta}^{2}, \label{27.9.1}\]

onde\(I_{0}\) está a intensidade da onda polarizada antes de passar pelo filtro. A equação\ ref {27.9.1} é conhecida como lei de Malus.

Figura\(\PageIndex{6}\): O efeito da rotação de dois filtros polarizadores, onde o primeiro polariza a luz. (a) Toda a luz polarizada é passada pelo segundo filtro polarizador, porque seu eixo é paralelo ao primeiro. (b) Quando a segunda é girada, apenas parte da luz passa. (c) Quando o segundo é perpendicular ao primeiro, nenhuma luz é passada. (d) Nesta fotografia, um filtro polarizador é colocado acima de dois outros. Seu eixo é perpendicular ao filtro à direita (área escura) e paralelo ao filtro à esquerda (área mais clara). (crédito: P.P. Urone)

Figura\(\PageIndex{7}\): Um filtro polarizador transmite somente o componente da onda paralelo ao seu eixo\(E\cos{\theta}\), reduzindo a intensidade de qualquer luz não polarizada paralelamente ao seu eixo.

Exemplo\(\PageIndex{1}\): Calculating Intensity Reduction by a Polarizing Filter

Qual ângulo é necessário entre a direção da luz polarizada e o eixo de um filtro polarizador para reduzir sua intensidade em\(90.0 \% \)?

Estratégia:

Quando a intensidade é reduzida em\(90.0 \%\), ela é\(10.0 \%\) ou 0,100 vezes seu valor original. Isso é,\(I = 0.100 I_{0}\). Usando essas informações, a equação\(I = I_{0}\cos{\theta}^{2}\) pode ser usada para resolver o ângulo necessário.

Solução

Resolvendo a equação\(I = I_{0} \cos{\theta}^{2}\)\(\cos{\theta}\) e substituindo pela relação entre\(I\) e\(I_{0}\) dá

\[\cos{\theta} = \sqrt{\frac{I}{I_{0}}} = \sqrt{\frac{0.100I_{0}}{I_{0}}} = 0.3162.\label{27.9.2}\]

Solução para obter\(\theta\) rendimentos

\[\theta = \cos{0.3162}^{-2} = 71.6^{\circ} \label{27.9.3}\]

Discussão:

É necessário um ângulo bastante grande entre a direção da polarização e o eixo do filtro para reduzir a\(10.0 \%\) intensidade ao valor original. Isso parece razoável com base em experiências com filmes polarizadores. É interessante que, em um ângulo de\(45^{\circ}\), a intensidade seja reduzida ao\(50\%\) seu valor original (como você mostrará nesta seção Problemas e exercícios). Observe que\(71.6^{\circ}\) é a redução\(18.4^{\circ}\) da intensidade para zero e que em um ângulo\(18.4^{\circ}\) da intensidade é reduzido ao\(90.0\%\) valor original (como você também mostrará em Problemas e Exercícios), evidenciando simetria.

Polarização por reflexão

Agora você provavelmente pode adivinhar que os óculos de sol Polaroid reduzem o brilho da luz refletida porque essa luz é polarizada. Você pode verificar isso por si mesmo segurando os óculos de sol Polaroid à sua frente e girando-os enquanto observa a luz refletida na água ou no vidro. Ao girar os óculos de sol, você notará que a luz fica clara e fraca, mas não completamente preta. Isso implica que a luz refletida está parcialmente polarizada e não pode ser completamente bloqueada por um filtro polarizador.

A Figura 8 ilustra o que acontece quando a luz não polarizada é refletida de uma superfície. A luz polarizada verticalmente é preferencialmente refratada na superfície, para que a luz refletida fique mais polarizada horizontalmente. As razões para esse fenômeno estão além do escopo deste texto, mas um mnemônico conveniente para lembrar isso é imaginar a direção da polarização como uma flecha. A polarização vertical seria como uma seta perpendicular à superfície e teria maior probabilidade de grudar e não ser refletida. A polarização horizontal é como uma flecha saltando de lado e teria maior probabilidade de ser refletida. Óculos de sol com eixos verticais bloqueariam então mais luz refletida do que luz não polarizada de outras fontes.

Figura\(\PageIndex{8}\): Polarização por reflexão. A luz não polarizada tem quantidades iguais de polarização vertical e horizontal. Após a interação com uma superfície, os componentes verticais são preferencialmente absorvidos ou refratados, deixando a luz refletida mais polarizada horizontalmente. Isso é semelhante às flechas batendo nas laterais ricocheteando, enquanto as flechas que atingem suas pontas vão para a superfície.

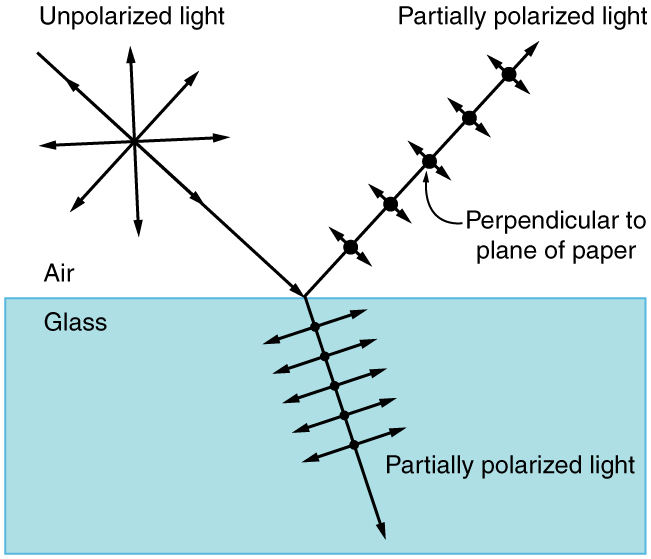
Como a parte da luz que não é refletida é refratada, a quantidade de polarização depende dos índices de refração do meio envolvido. Pode-se mostrar que a luz refletida é completamente polarizada em um ângulo de reflexão\(\theta_{b}\), dado por\[\tan{\theta_{b}} = \frac{n_{2}}{n_{1}}, \label{27.9.4}\] onde\(n_{1}\) está o meio no qual a luz incidente e refletida viajam e\(n_{2}\) é o índice de refração do meio que forma a interface que reflete a luz. Essa equação é conhecida como lei de Brewster e\(\theta_{b}\) é conhecida como ângulo de Brewster, em homenagem ao físico escocês do século XIX que os descobriu.

COISAS GRANDES E PEQUENAS: EXPLICAÇÃO ATÔMICA DOS FILTROS POLARIZADORES:

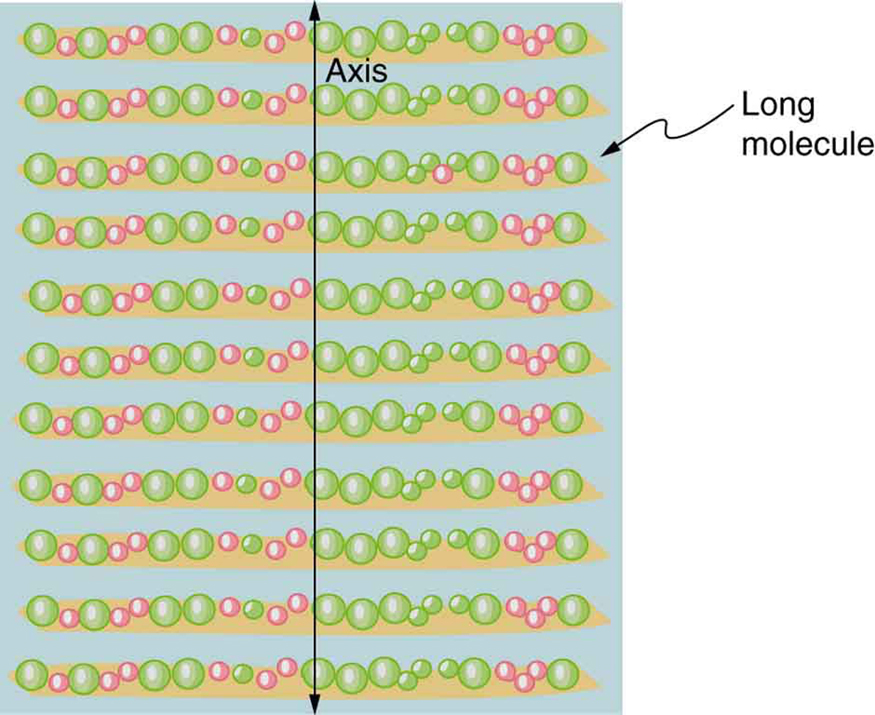
Os filtros polarizadores têm um eixo de polarização que atua como uma fenda. Essa fenda passa por ondas eletromagnéticas (geralmente luz visível) que têm um campo elétrico paralelo ao eixo. Isso é feito com moléculas longas alinhadas perpendicularmente ao eixo, conforme mostrado na Figura 9.

Figura\(\PageIndex{9}\): As moléculas longas estão alinhadas perpendicularmente ao eixo de um filtro polarizador. O componente do campo elétrico em uma onda EM perpendicular a essas moléculas passa pelo filtro, enquanto o componente paralelo às moléculas é absorvido.

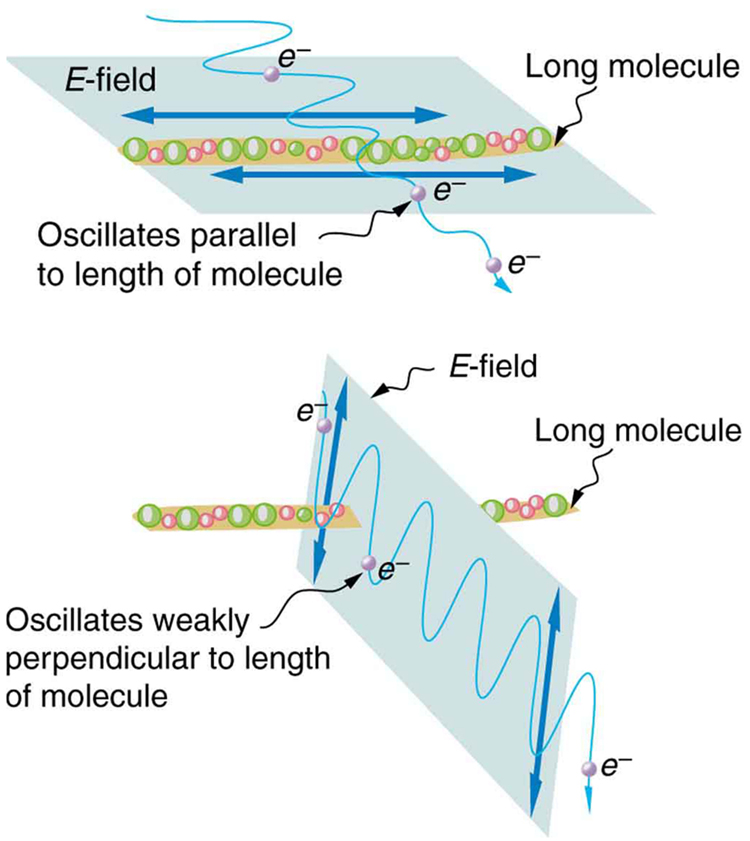
A Figura 10 ilustra como o componente do campo elétrico paralelo às moléculas longas é absorvido. Uma onda eletromagnética é composta por campos elétricos e magnéticos oscilantes. O campo elétrico é forte em comparação com o campo magnético e é mais eficaz em exercer força sobre as cargas nas moléculas. As partículas carregadas mais afetadas são os elétrons nas moléculas, já que as massas de elétrons são pequenas. Se o elétron for forçado a oscilar, ele pode absorver energia da onda EM. Isso reduz os campos na onda e, portanto, reduz sua intensidade. Em moléculas longas, os elétrons podem oscilar mais facilmente paralelamente à molécula do que na direção perpendicular. Os elétrons estão ligados à molécula e são mais restritos em seu movimento perpendicular à molécula. Assim, os elétrons podem absorver ondas EM que têm um componente de seu campo elétrico paralelo à molécula. Os elétrons são muito menos responsivos aos campos elétricos perpendiculares à molécula e permitirão que esses campos passem. Assim, o eixo do filtro polarizador é perpendicular ao comprimento da molécula.

Figura\(\PageIndex{10}\): Concepção artística de um elétron em uma molécula longa oscilando paralelamente à molécula. A oscilação do elétron absorve energia e reduz a intensidade do componente da onda EM que é paralelo à molécula.

Exemplo\(\PageIndex{2}\): Calculating Polarization by Reflection

1. Em que ângulo a luz que viaja no ar será completamente polarizada horizontalmente quando refletida pela água?
2. De vidro?

Estratégia:

Tudo o que precisamos para resolver esses problemas são os índices de refração. O ar tem\(n_{1} = 100\), a água tem\(n_{2} = 1.333\) e o vidro da coroa tem\(n'_{2} = 1.520\). A equação\(\tan{\theta_{b}} = \frac{n_{2}}{n_{1}}\) pode ser aplicada diretamente para encontrar\(\theta_{b}\) em cada caso.

Solução (a):

Colocando as quantidades conhecidas na equação

\[\tan{\theta_{b}} = \frac{n_{2}}{n_{1}} \label{27.9.4}\]

concede

\[\tan{\theta_{b}} = \frac{n_{2}}{n_{1}} = \frac{1.333}{1.00} = 1.333.\]

Resolver o ângulo\(\theta_{b}\) produz

\[\theta_{b} = \tan{1.333}^{-1} = 53.1^{\circ}.\]

Solução (b):

Da mesma forma, para coroa de vidro e ar,\[\tan{\theta_{b}'} = \frac{n'_{2}}{n_{1}} = \frac{1.520}{1.00} = 1.52.\] portanto,\[\theta_{b}' = \tan{1.52}^{-1} = 56.7^{\circ}.\]

Discussão:

A luz refletida nesses ângulos pode ser completamente bloqueada por um bom filtro polarizador mantido com seu eixo vertical. O ângulo de Brewster para água e ar é semelhante ao do vidro e do ar, de modo que os óculos de sol são igualmente eficazes para a luz refletida pela água ou pelo vidro em circunstâncias semelhantes. A luz não refletida é refratada nesses meios. Portanto, em um ângulo de incidência igual ao ângulo de Brewster, a luz refratada será levemente polarizada verticalmente. Não será completamente polarizado verticalmente, porque apenas uma pequena fração da luz incidente é refletida e, portanto, uma quantidade significativa de luz polarizada horizontalmente é refratada.

Polarização por dispersão

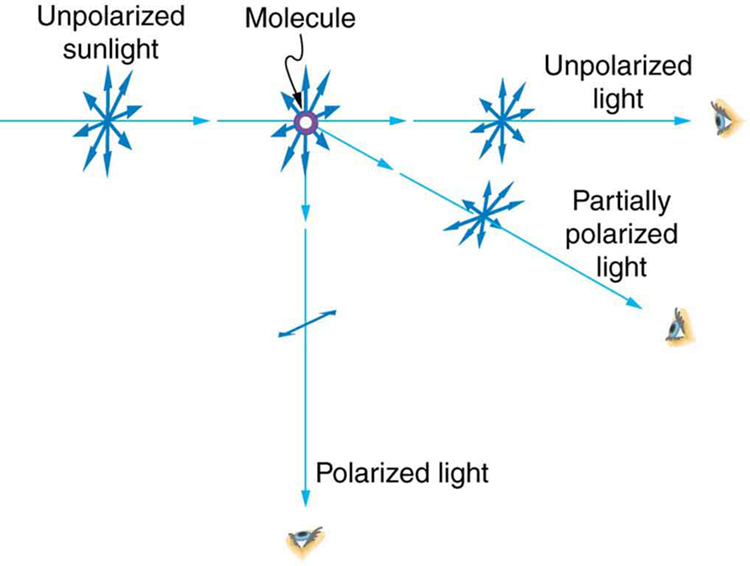
Se você segurar seus óculos de sol Polaroid à sua frente e girá-los enquanto olha para o céu azul, você verá o céu ficar claro e escuro. Essa é uma indicação clara de que a luz dispersa pelo ar está parcialmente polarizada. \(\PageIndex{11}\)A figura ajuda a ilustrar como isso acontece. Como a luz é uma onda EM transversal, ela vibra os elétrons das moléculas de ar perpendicularmente à direção em que está viajando. Os elétrons então irradiam como pequenas antenas. Como eles estão oscilando perpendicularmente à direção do raio de luz, eles produzem radiação EM que é polarizada perpendicularmente à direção do raio. Ao visualizar a luz ao longo de uma linha perpendicular ao raio original, como na Figura 11, não pode haver polarização na luz dispersa paralela ao raio original, pois isso exigiria que o raio original fosse uma onda longitudinal. Em outras direções, um componente da outra polarização pode ser projetado ao longo da linha de visão, e a luz dispersa só será parcialmente polarizada. Além disso, a dispersão múltipla pode trazer luz aos olhos de outras direções e conter diferentes polarizações.

Figura\(\PageIndex{11}\): Polarização por dispersão. A dispersão de luz não polarizada das moléculas de ar sacude seus elétrons perpendicularmente à direção do raio original. A luz dispersa, portanto, tem uma polarização perpendicular à direção original e nenhuma paralela à direção original.

As fotografias do céu podem ser escurecidas por filtros polarizadores, um truque usado por muitos fotógrafos para tornar as nuvens mais brilhantes em contraste. A dispersão de outras partículas, como fumaça ou poeira, também pode polarizar a luz. Detectar a polarização em ondas EM dispersas pode ser uma ferramenta analítica útil para determinar a fonte de dispersão.

Há uma variedade de efeitos ópticos usados em óculos de sol. Além de serem Polaroid, outros óculos de sol têm pigmentos coloridos embutidos neles, enquanto outros usam revestimentos não refletivos ou mesmo refletivos. Um desenvolvimento recente são as lentes fotocrômicas, que escurecem à luz do sol e ficam claras em ambientes fechados. As lentes fotocrômicas são incorporadas com moléculas microcristalinas orgânicas que mudam suas propriedades quando expostas aos raios UV da luz solar, mas ficam claras na iluminação artificial sem UV.

EXPERIÊNCIA PARA LEVAR PARA CASA: POLARIZAÇÃO

Encontre óculos de sol Polaroid e gire um enquanto segura o outro imóvel e observe diferentes superfícies e objetos. Explique suas observações. Qual é a diferença no ângulo de quando você vê uma intensidade máxima até quando você vê uma intensidade mínima? Encontre uma superfície de vidro refletivo e faça o mesmo. Em que ângulo o vidro precisa ser orientado para dar o mínimo de brilho?

Cristais líquidos e outros efeitos de polarização em materiais

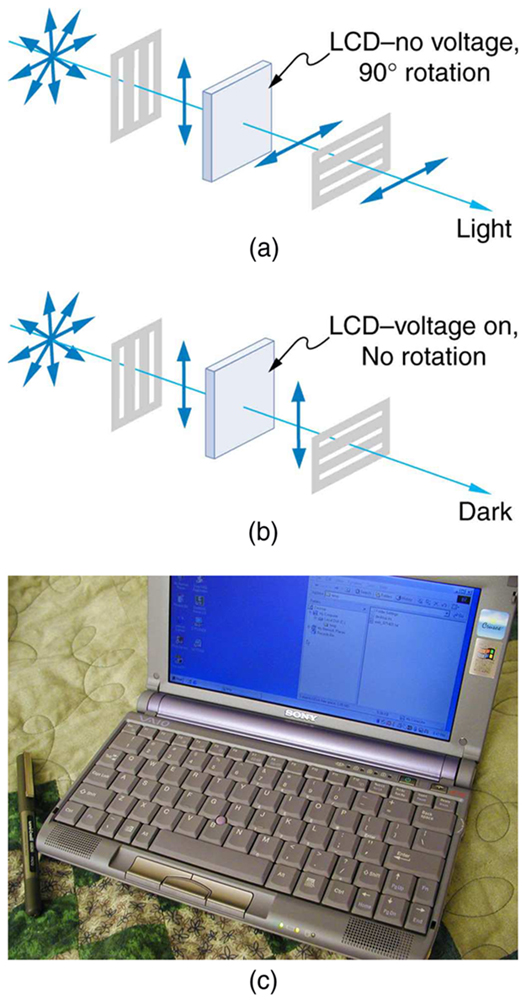
Embora você esteja, sem dúvida, ciente das telas de cristal líquido (LCDs) encontradas em relógios, calculadoras, telas de computador, telefones celulares, televisores de tela plana e outros inúmeros lugares, você pode não estar ciente de que elas são baseadas na polarização. Os cristais líquidos são assim chamados porque suas moléculas podem ser alinhadas mesmo estando em um líquido. Os cristais líquidos têm a propriedade de girar a polarização da luz que passa por eles\(90^{\circ}\). Além disso, essa propriedade pode ser desativada pela aplicação de uma tensão, conforme ilustrado na Figura\(\PageIndex{12}\). É possível manipular essa característica rapidamente e em pequenas regiões bem definidas para criar os padrões de contraste que vemos em tantos dispositivos LCD.

Nas TVs LCD de tela plana, há uma grande luz na parte traseira da TV. A luz viaja para a tela frontal através de milhões de pequenas unidades chamadas pixels (elementos de imagem). Uma delas é mostrada na Figura\(\PageIndex{12a}\)\(\PageIndex{12b}\) e. Cada unidade tem três células, com filtros vermelhos, azuis ou verdes, cada uma controlada de forma independente. Quando a tensão em um cristal líquido é desligada, o cristal líquido passa a luz pelo filtro específico. Pode-se variar o contraste da imagem variando a intensidade da tensão aplicada ao cristal líquido.

Figura\(\PageIndex{12}\): (a) A luz polarizada é girada\(90^{\circ}\) por um cristal líquido e depois passada por um filtro polarizador que tem seu eixo perpendicular à direção original de polarização. (b) Quando uma tensão é aplicada ao cristal líquido, a luz polarizada não é girada e é bloqueada pelo filtro, tornando a região escura em comparação com o ambiente. (c) Os LCDs podem ser feitos com cores específicas, pequenos e rápidos o suficiente para serem usados em laptops e TVs. (crédito: Jon Sullivan)

Muitos cristais e soluções giram o plano de polarização da luz que passa por eles. Diz-se que essas substâncias são opticamente ativas. Os exemplos incluem água com açúcar, insulina e colágeno (Figura\(\PageIndex{13}\)). Além de depender do tipo de substância, a quantidade e a direção da rotação dependem de vários fatores. Entre elas está a concentração da substância, a distância que a luz percorre e o comprimento de onda da luz. A atividade óptica se deve à forma assimétrica das moléculas na substância, como a helicoidal. Medições da rotação da luz polarizada passando por substâncias podem, portanto, ser usadas para medir as concentrações, uma técnica padrão para açúcares. Também pode fornecer informações sobre as formas das moléculas, como proteínas, e fatores que afetam suas formas, como temperatura e pH.

Figura\(\PageIndex{13}\): A atividade óptica é a capacidade de algumas substâncias girarem o plano de polarização da luz que passa por elas. A rotação é detectada com um filtro ou analisador polarizador.

Vidro e plástico se tornam opticamente ativos quando estressados; quanto maior o estresse, maior o efeito. A análise de tensão óptica em formas complicadas pode ser realizada fazendo modelos plásticos delas e observando-as por meio de filtros cruzados, conforme visto na Figura 14. É evidente que o efeito depende do comprimento de onda e do estresse. Às vezes, a dependência do comprimento de onda também é usada para fins artísticos.

Figura\(\PageIndex{14}\): Análise de tensão óptica de uma lente de plástico colocada entre polarizadores cruzados. (crédito: Infopro, Wikimedia Commons)

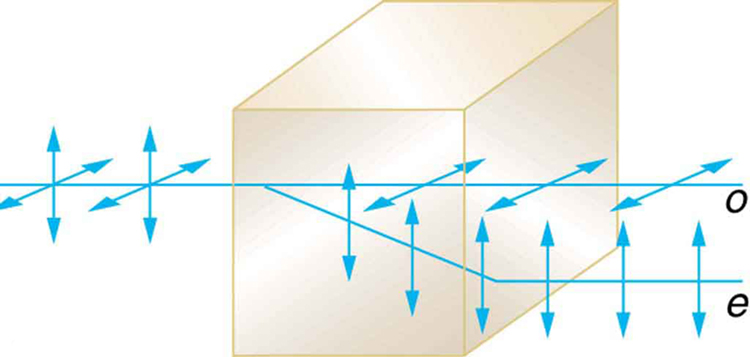
Outro fenômeno interessante associado à luz polarizada é a capacidade de alguns cristais de dividir um feixe de luz não polarizado em dois. Diz-se que esses cristais não são refringentes (veja a Figura 15). Cada um dos raios separados tem uma polarização específica. Um se comporta normalmente e é chamado de raio comum, enquanto o outro não obedece à lei de Snell e é chamado de raio extraordinário. Cristais birrefringentes podem ser usados para produzir feixes polarizados a partir de luz não polarizada. Alguns materiais birrefringentes absorvem preferencialmente uma das polarizações. Esses materiais são chamados de dicróicos e podem produzir polarização por essa absorção preferencial. É basicamente assim que os filtros polarizadores e outros polarizadores funcionam. O leitor interessado é convidado a aprofundar as inúmeras propriedades dos materiais relacionadas à polarização.

Figura\(\PageIndex{15}\): Materiais birrefringentes, como o mineral comum calcita, dividem feixes de luz não polarizados em dois. O raio comum se comporta conforme o esperado, mas o raio extraordinário não obedece à lei de Snell.

Resumo

• A polarização é o atributo de que as oscilações das ondas têm uma direção definida em relação à direção de propagação da onda.
• As ondas EM são ondas transversais que podem ser polarizadas.
• A direção da polarização é definida como sendo a direção paralela ao campo elétrico da onda EM.
• A luz não polarizada é composta por muitos raios com direções de polarização aleatórias.
• A luz pode ser polarizada passando-a através de um filtro polarizador ou outro material polarizador. A intensidade\(I\) da luz polarizada após passar por um filtro polarizador é\(I = I_{0}\cos{\theta}^{2}\), onde\(I_{0}\) está a intensidade original e\(\theta\) é o ângulo entre a direção da polarização e o eixo do filtro.
• A polarização também é produzida pela reflexão.
• A lei de Brewster afirma que a luz refletida será completamente polarizada no ângulo de reflexão\(\theta_{b}\), conhecido como ângulo de Brewster, dado por uma declaração conhecida como lei de Brewster:\(\tan{\theta_{b}} = \frac{n_{2}}{n_{1}}\), onde\(n_{1}\) está o meio no qual a luz incidente e refletida viajam e\(n_{2}\) é o índice de refração do meio que forma a interface que reflete a luz.
• A polarização também pode ser produzida por dispersão.
• Existem vários tipos de substâncias opticamente ativas que giram na direção da polarização da luz que passa por elas.

Glossário

eixo de um filtro polarizador

a direção na qual o filtro passa pelo campo elétrico de uma onda EM

birrefringente

cristais que dividem um feixe de luz não polarizado em dois feixes

O ângulo de Brewster

\(\theta_{b} = \tan{\left(\frac{n_{2}}{n_{1}}\right)}^{-1}\), onde\(n_{2}\) é o índice de refração do meio do qual a luz é refletida e\(n_{1}\) é o índice de refração do meio no qual a luz refletida viaja

Lei de Brewster

\(\tan{\theta_{b}} = \frac{n_{2}}{n_{1}}\), onde\(n_{1}\) é o meio no qual a luz incidente e refletida viaja e\(n_{2}\) é o índice de refração do meio que forma a interface que reflete a luz

direção da polarização

a direção paralela ao campo elétrico para ondas EM

polarizado horizontalmente

as oscilações estão em um plano horizontal

opticamente ativo

substâncias que giram o plano de polarização da luz que passa por elas

polarização

o atributo de que as oscilações das ondas têm uma direção definida em relação à direção de propagação da onda

polarizado

ondas com oscilações do campo elétrico e magnético em uma direção definida

luz refletida que é completamente polarizada

luz refletida no ângulo de reflexão\(\theta_{b}\), conhecido como ângulo de Brewster

não polarizado

ondas que são polarizadas aleatoriamente

polarizado verticalmente

as oscilações estão em um plano vertical