27.7: Interferência de filme fino

Last updated
Save as PDF

Page ID: 194422

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Discuta a formação do arco-íris por filmes finos.

As cores brilhantes vistas em uma mancha de óleo flutuando na água ou em uma bolha de sabão iluminada pelo sol são causadas por interferência. As cores mais brilhantes são aquelas que interferem de forma construtiva. Essa interferência ocorre entre a luz refletida de diferentes superfícies de um filme fino; portanto, o efeito é conhecido como interferência de filme fino. Conforme observado anteriormente, os efeitos de interferência são mais proeminentes quando a luz interage com algo que tem um tamanho semelhante ao seu comprimento de onda. Uma película fina é aquela que tem uma espessura\(t\) menor do que algumas vezes o comprimento de onda da luz,\(\lambda\). Como a cor está associada indiretamente\(\lambda\) e como toda interferência depende de alguma forma da proporção em relação\(\lambda\) ao tamanho do objeto envolvido, devemos esperar ver cores diferentes para diferentes espessuras de um filme, como na Figura\(\PageIndex{1}\).

Bolhas de sabão refletindo principalmente luz roxa e azul com algumas regiões de laranja. — Figura\(\PageIndex{1}\): Essas bolhas de sabão exibem cores brilhantes quando expostas à luz solar. (crédito: Scott Robinson, Flickr).

O que causa interferência em filmes finos? A Figura 2 mostra como a luz refletida das superfícies superior e inferior de um filme pode interferir. A luz incidente é refletida apenas parcialmente da superfície superior do filme (raio 1). O restante entra no filme e é parcialmente refletido pela superfície inferior. Parte da luz refletida da superfície inferior pode emergir da parte superior do filme (raio 2) e interferir com a luz refletida da parte superior (raio 1). Como o raio que entra no filme percorre uma distância maior, ele pode estar dentro ou fora de fase com o raio refletido de cima. No entanto, considere por um momento, novamente, as bolhas na Figura\(\PageIndex{1}\). As bolhas são mais escuras onde são mais finas. Além disso, se você observar uma bolha de sabão com cuidado, notará que ela escurece no ponto em que se rompe. Para filmes muito finos, a diferença nos comprimentos dos caminhos do raio 1 e do raio 2 na Figura\(\PageIndex{2}\) é insignificante; então, por que eles deveriam interferir de forma destrutiva e não construtiva? A resposta é que uma mudança de fase pode ocorrer após a reflexão. A regra é a seguinte:

Quando a luz reflete de um meio com um índice de refração maior do que o do meio no qual está viajando, ocorre uma mudança de\(180^{\circ}\) fase (ou a\(\lambda /2\)).

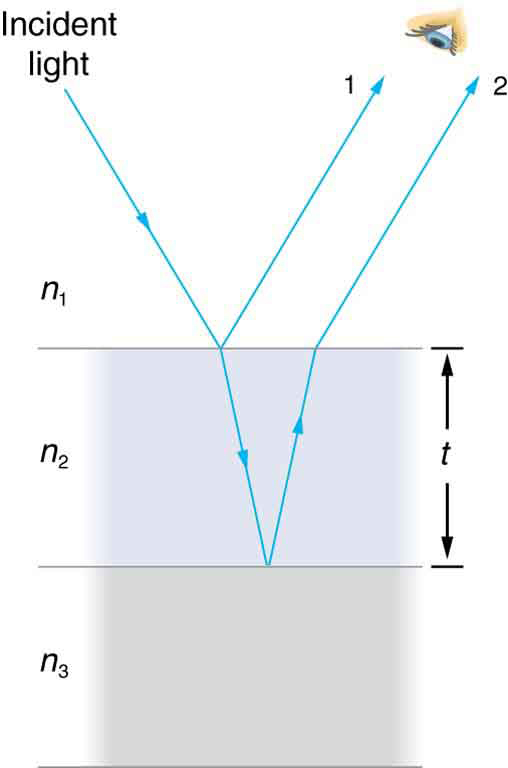
A figura mostra três materiais, ou mídia, empilhados um sobre o outro. O meio superior é rotulado em um, o próximo é rotulado em dois e sua espessura é t, e o menor é rotulado em três. Um raio de luz chamado luz incidente começa no meio n e se propaga para baixo e para a direita para atingir a interface n um n dois. O raio é parcialmente refletido e parcialmente refratado. O raio parcialmente refletido é rotulado como raio um. O raio refratado continua para baixo no meio n dois e é refletido de volta pela interface n dois n três. Esse raio refletido, denominado raio dois, refrata novamente ao passar pela interface n dois n um e continua ascendendo paralelamente ao raio um. O raio um e o raio dois entram no olho do observador. — Figura\(\PageIndex{2}\): A luz que atinge uma película fina é parcialmente refletida (raio 1) e parcialmente refratada na superfície superior. O raio refratado é parcialmente refletido na superfície inferior e emerge como raio 2. Esses raios interferirão de uma forma que depende da espessura do filme e dos índices de refração dos vários meios.

No filme da Figura\(\PageIndex{2}\) há uma bolha de sabão (essencialmente água com ar em ambos os lados), depois há uma\(\lambda / 2\) mudança para o raio 1 e nenhuma para o raio 2. Assim, quando o filme é muito fino, a diferença de comprimento do caminho entre os dois raios é insignificante, eles estão exatamente fora de fase e interferências destrutivas ocorrerão em todos os comprimentos de onda e, portanto, a bolha de sabão ficará escura aqui.

A espessura do filme em relação ao comprimento de onda da luz é outro fator crucial na interferência do filme fino. O raio 2 na Figura\(\PageIndex{2}\) percorre uma distância maior do que o raio 1. Para a luz incidente perpendicular à superfície, o raio 2 percorre uma\(2t\) distância aproximadamente maior do que o raio 1. Quando essa distância é um múltiplo integral ou semi-integral do comprimento de onda no meio (\(\lambda_{n} = \lambda / n\), onde\(\lambda\) é o comprimento de onda no vácuo e\(n\) é o índice de refração), ocorre interferência construtiva ou destrutiva, dependendo também de haver uma mudança de fase em qualquer um dos raios.

Exemplo\(\PageIndex{1}\): Calculating Non-reflective Lens Coating Using Thin Film Interference

Câmeras sofisticadas usam uma série de várias lentes. A luz pode refletir nas superfícies dessas várias lentes e degradar a clareza da imagem. Para limitar esses reflexos, as lentes são revestidas com uma fina camada de fluoreto de magnésio que causa interferência destrutiva na película fina. Qual é o mais fino que esse filme pode ser, se seu índice de refração for 1,38 e for projetado para limitar a reflexão da luz de 550 nm, normalmente o comprimento de onda visível mais intenso? O índice de refração do vidro é 1,52.

Estratégia

Consulte a Figura\(\PageIndex{2}\) e use\(n_{1} = 1.00\) para ar\(n_{2} = 1.38\),\(n_{3} = 1.52\) e. Tanto o raio 1 quanto o raio 2 terão uma\(\lambda / 2\) mudança após a reflexão. Assim, para obter interferência destrutiva, o raio 2 precisará percorrer meio comprimento de onda a mais do que o raio 1. Para raios incidentes perpendicularmente, a diferença de comprimento do caminho é\(2t\).

Solução

Para obter interferência destrutiva aqui,

\[2t = \frac{\lambda_{n_{2}}}{2}, \nonumber\]

onde\(\lambda_{n_{2}}\) está o comprimento de onda no filme e é dado por\(\lambda_{n_{2}} = \frac{\lambda}{n_{2}}\).

Assim,

\[2t = \frac{\lambda / n_{2}}{2}.\nonumber\]

Resolver\(t\) e inserir valores conhecidos gera

\[ \begin{align*} t &= \frac{\lambda / n_{2}}{4} \\[4pt] &= \frac{\left(550 nm \right) / 1.38}{4} \\[4pt] &= 99.6 nm. \end{align*}\]

Discussão

Filmes como o deste exemplo são mais eficazes na produção de interferência destrutiva quando a camada mais fina é usada, pois a luz em uma faixa mais ampla de ângulos de incidência será reduzida em intensidade. Esses filmes são chamados de revestimentos não refletivos; essa é apenas uma descrição aproximadamente correta, pois outros comprimentos de onda serão cancelados apenas parcialmente. Revestimentos não refletivos são usados nas janelas e óculos de sol dos carros.

A interferência de filme fino é mais construtiva ou mais destrutiva quando a diferença de comprimento do caminho para os dois raios é um comprimento de onda integral ou meio integral, respectivamente. Ou seja, para raios incidentes perpendicularmente,\(2t = \lambda_{n}, 2\lambda_{n}, 3\lambda_{n},...\) ou\(2t = \lambda_{n}/2, 3\lambda_{n}/2, 5\lambda_{n}/2,...\) Para saber se a interferência é construtiva ou destrutiva, você também deve determinar se há uma mudança de fase após a reflexão. A interferência do filme fino, portanto, depende da espessura do filme, do comprimento de onda da luz e dos índices de refração. Para a luz branca incidente em um filme que varia em espessura, você observará as cores do arco-íris de interferência construtiva em vários comprimentos de onda à medida que a espessura varia.

Exemplo\(\PageIndex{2}\): Soap Bubbles: More Than One Thickness can be Constructive

Quais são as três menores espessuras de uma bolha de sabão que produzem interferência construtiva para luz vermelha com comprimento de onda de 650 nm? O índice de refração do sabão é considerado o mesmo da água.
Quais são as três menores espessuras que causarão interferência destrutiva?

Estratégia e conceito:

Use\(\PageIndex{2}\) a Figura para visualizar a bolha. Observe isso\(n_{1} = n_{3} = 1.00\) para ar e\(n_{2} = 1.333\) sabão (equivalente a água). Há um\(\lambda / 2\) desvio para o raio 1 refletido da superfície superior da bolha e nenhum deslocamento para o raio 2 refletido da superfície inferior. Para obter interferência construtiva, então, a diferença do comprimento do caminho (\(2t\)) deve ser um múltiplo semi-integral do comprimento de onda - sendo os três primeiros\(\lambda_{n}/2, 3\lambda_{n}/2\),\(5\lambda_{n}/2\) e. Para obter interferência destrutiva, a diferença do comprimento do caminho deve ser um múltiplo integral do comprimento de onda - os três primeiros são\(0, \lambda_{n},\)\(2\lambda_{n}\) e.

Solução (a):

A interferência construtiva ocorre aqui quando

\[2t_{c} = \frac{\lambda_{n}}{2}, \frac{3\lambda_{n}}{2}, \frac{5\lambda_{n}}{2},...\label{27.8.4}\]

A menor espessura construtiva\(t_{c}\), portanto, é

\[ \begin{align*} t_{c} &= \frac{\lambda_{n}}{4} = \frac{\lambda / n}{4} \\[4pt] &= \frac{\left(650 nm\right) / 1.333}{4} \label{27.8.5} \\[4pt] &= 122 nm. \end{align*}\]

A próxima espessura que fornece interferência construtiva é\(t'_{c} = 3\lambda_{n}/4\), de modo que

\[t'_{c} = 366 nm. \label{27.8.6} \nonumber\]

Finalmente, a terceira espessura que produz interferência construtiva é\(t''_{c} \lt 5\lambda_{n} / 4\), de modo que

\[t''_{c} = 610 nm. \label{27.8.7} \nonumber\]

Solução (b):

Para interferência destrutiva, a diferença do comprimento do caminho aqui é um múltiplo integral do comprimento de onda. A primeira ocorre com espessura zero, pois há uma mudança de fase na superfície superior. Ou seja,

\[t_{d} = 0. \label{27.8.8}\]

A primeira espessura diferente de zero produzindo interferência destrutiva é

\[2t'_{d} = \lambda_{n}. \label{27.8.9}\]

A substituição de valores conhecidos fornece

\[t'_{d} = \frac{\lambda_{n}}{2} = \frac{\lambda / n}{2} = \frac{\left(650 nm \right) / 1.333}{2} \label{27.8.10}\]\[= 244 nm.\]Finalmente, a terceira espessura destrutiva é\(2t''_{d} = 2\lambda_{n}\), de modo que

\[t''_{d} = \lambda_{n} = \frac{\lambda}{n} = \frac{650 nm}{1.333} \label{27.8.11}\]\[= 488 nm.\]

Discussão:

Se a bolha fosse iluminada com pura luz vermelha, veríamos faixas claras e escuras com aumentos de espessura muito uniformes. Primeiro seria uma faixa escura com 0 de espessura, depois brilhante a 122 nm de espessura, depois escura a 244 nm, brilhante a 366 nm, escura a 488 nm e brilhante a 610 nm. Se a espessura da bolha variasse suavemente, como uma cunha lisa, as faixas seriam espaçadas uniformemente.

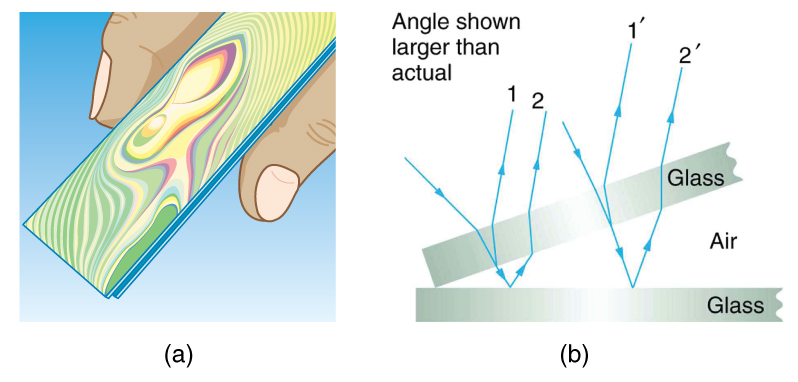
Outro exemplo de interferência de filme fino pode ser visto quando as lâminas do microscópio são separadas (Figura\(\PageIndex{3}\)). As lâminas são muito planas, de modo que a borda de ar entre elas aumenta de espessura de maneira muito uniforme. Uma mudança de fase ocorre na segunda superfície, mas não na primeira, e, portanto, há uma faixa escura onde os slides se tocam. As cores do arco-íris da interferência construtiva se repetem, indo do violeta ao vermelho repetidamente à medida que a distância entre as lâminas aumenta. À medida que a camada de ar aumenta, as faixas se tornam mais difíceis de ver, porque pequenas mudanças no ângulo de incidência têm maiores efeitos nas diferenças de comprimento do caminho. Se for usada luz de comprimento de onda puro em vez de luz branca, faixas claras e escuras serão obtidas em vez de repetir as cores do arco-íris.

A Figura A mostra duas lâminas de microscópio que foram pressionadas juntas. Faixas de arco-íris em espiral multicoloridas são visíveis provenientes dos slides. A Figura B mostra uma seção transversal de duas lâminas de vidro empilhadas uma sobre a outra. O slide inferior é horizontal e o slide superior é inclinado para cima em um ângulo maior do que o ângulo real entre os slides. Dois raios vêm de cima e colidem com as lâminas. Sua refração e reflexão parcial são mostradas em cada interface de ar de vidro. — Figura\(\PageIndex{3}\): (a) As faixas coloridas do arco-íris são produzidas pela interferência de filme fino no ar entre as duas lâminas de vidro. (b) Esquema dos caminhos percorridos pelos raios na cunha de ar entre as lâminas.

Uma aplicação importante da interferência de película fina é encontrada na fabricação de instrumentos ópticos. Uma lente ou espelho pode ser comparado a um mestre quando está sendo retificado, permitindo que seja moldado com uma precisão de menos de um comprimento de onda em toda a sua superfície. A figura\(\PageIndex{4}\) ilustra o fenômeno chamado anéis de Newton, que ocorre quando as superfícies planas de duas lentes são colocadas juntas. (As faixas circulares são chamadas de anéis de Newton porque Isaac Newton as descreveu e seu uso em detalhes. Newton não os descobriu; Robert Hooke sim, e Newton não acreditava que fossem devidos ao caráter ondulatório da luz.) Cada anel sucessivo de uma determinada cor indica um aumento de apenas um comprimento de onda na distância entre a lente e o espaço em branco, para que uma grande precisão possa ser obtida. Quando a lente estiver perfeita, não haverá anéis.

Esta figura mostra anéis concêntricos da cor do arco-íris obtidos quando duas lentes plano-convexas são colocadas junto com suas superfícies planas em contato. — Figura\(\PageIndex{4}\): As franjas de interferência dos “anéis de Newton” são produzidas quando duas lentes plano-convexas são colocadas junto com suas superfícies planas em contato. Os anéis são criados pela interferência entre a luz refletida pelas duas superfícies como resultado de um pequeno espaço entre elas, indicando que essas superfícies não são precisamente planas, mas são ligeiramente convexas. (crédito: Ulf Seifert, Wikimedia Commons)

As asas de certas mariposas e borboletas têm cores quase iridescentes devido à interferência do filme fino. Além da pigmentação, a cor da asa é muito afetada pela interferência construtiva de certos comprimentos de onda refletidos em sua superfície revestida por película. Os fabricantes de automóveis estão oferecendo trabalhos de pintura especiais que usam interferência de filme fino para produzir cores que mudam com o ângulo. Essa opção cara é baseada na variação das diferenças de comprimento do caminho do filme fino com o ângulo. Os recursos de segurança em cartões de crédito, notas, carteiras de habilitação e itens similares propensos à falsificação usam interferência de filme fino, grades de difração ou hologramas. A Austrália liderou com notas de dólar impressas em polímero com um recurso de segurança de grade de difração que dificulta a falsificação da moeda. Outros países, como Nova Zelândia e Taiwan, estão usando tecnologias semelhantes, enquanto a moeda dos Estados Unidos inclui um efeito de interferência de filme fino.

FAZENDO CONEXÕES: EXPERIMENTO PARA LEVAR PARA CASA — INTERFERÊNCIA DE FILME FINO

Uma característica das grades de difração e interferência de filme fino é que o padrão muda à medida que você altera o ângulo em que olha ou move a cabeça. Encontre exemplos de interferência de película fina e grades ao seu redor. Explique como os padrões mudam para cada exemplo específico. Encontre exemplos em que a espessura muda dando origem à mudança de cores. Se você encontrar duas lâminas de microscópio, tente observar o efeito mostrado na Figura 3. Tente separar uma extremidade das duas lâminas com um fio de cabelo ou talvez um pedaço de papel fino e observe o efeito.

Estratégias de resolução de problemas para óptica de ondas

Etapa 1. Examine a situação para determinar se há interferência envolvida. Identifique se fendas ou interferência de filme fino são consideradas no problema.
Etapa 2. Se houver fendas envolvidas, observe que grades de difração e fendas duplas produzem padrões de interferência muito semelhantes, mas que as grades têm máximos mais estreitos (mais nítidos). Os padrões de fenda única são caracterizados por um grande máximo central e máximos menores nas laterais.
Etapa 3. Se houver interferência de filme fino, observe a diferença de comprimento do caminho entre os dois raios que interferem. Certifique-se de usar o comprimento de onda no meio envolvido, pois ele difere do comprimento de onda no vácuo. Observe também que há uma mudança de\(\lambda / 2\) fase adicional quando a luz reflete de um meio com maior índice de refração.
Etapa 4. Identifique exatamente o que precisa ser determinado no problema (identifique as incógnitas). Uma lista escrita é útil. Desenhe um diagrama da situação. É útil rotular o diagrama.
Etapa 5. Faça uma lista do que é dado ou pode ser inferido do problema conforme declarado (identifique os conhecidos).
Etapa 6. Resolva a equação apropriada para a quantidade a ser determinada (a desconhecida) e insira os conhecidos. Fendas, grades e o limite de Rayleigh envolvem equações.
Etapa 7. Para interferência de filme fino, você terá interferência construtiva para uma mudança total que é um número integral de comprimentos de onda. Você terá interferência destrutiva para uma mudança total de um número meio integral de comprimentos de onda. Lembre-se sempre de que crista a crista é construtiva, enquanto crista a vale é destrutiva.
Etapa 8. Verifique se a resposta é razoável: Faz sentido? Os ângulos nos padrões de interferência não podem ser maiores do que\(90^{\circ}\), por exemplo.

Resumo

A interferência de filme fino ocorre entre a luz refletida das superfícies superior e inferior de um filme. Além da diferença de comprimento do caminho, pode haver uma mudança de fase.
Quando a luz reflete de um meio com um índice de refração maior do que o do meio no qual está viajando, ocorre uma mudança de\(180^{\circ}\) fase (ou\(\lambda /2\) mudança).

Glossário

interferência de filme fino: interferência entre a luz refletida de diferentes superfícies de um filme fino