Skip to main content
Global

27.5: Difração de fenda única

  1. Last updated
  2. Save as PDF
  • Page ID
    194398

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Discuta o padrão de difração de fenda única.

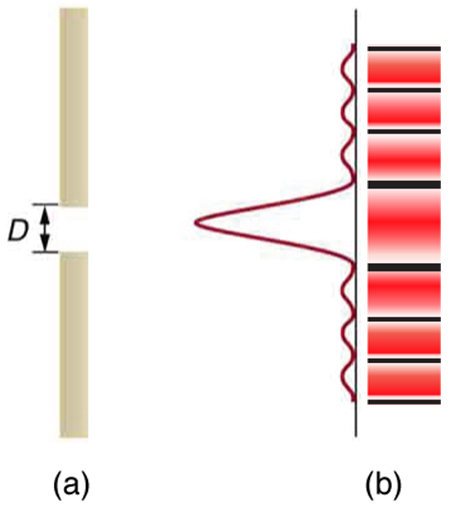
    A luz que passa por uma única fenda forma um padrão de difração um pouco diferente daqueles formados por fendas duplas ou grades de difração. A Figura 1 mostra um padrão de difração de fenda única. Observe que o máximo central é maior do que aqueles em ambos os lados e que a intensidade diminui rapidamente em ambos os lados. Em contraste, uma grade de difração produz linhas uniformemente espaçadas que escurecem lentamente em ambos os lados do centro.

    A parte a da figura mostra uma fenda em uma barra vertical. À direita da barra está um gráfico de intensidade versus altura. O gráfico é girado noventa graus no sentido anti-horário para que a escala de intensidade aumente para a esquerda e a altura aumente à medida que você sobe na página. Logo em frente à lacuna, um forte pico central se estende para a esquerda a partir da linha de base do gráfico, e muitos picos menores de satélite aparecem acima e abaixo desse pico central. A parte b da figura mostra um desenho do padrão de intensidade bidimensional que é observado a partir da difração de fenda única. A faixa central é bastante larga em comparação com as faixas de satélite, e há áreas escuras entre todas as faixas.
    Figura\(\PageIndex{1}\): (a) Padrão de difração de fenda única. A luz monocromática que passa por uma única fenda tem um máximo central e muitos máximos menores e mais escuros em ambos os lados. O máximo central é seis vezes maior do que o mostrado. (b) O desenho mostra o máximo central brilhante e os máximos mais escuros e mais finos em ambos os lados.

    A análise da difração de fenda única é ilustrada na Figura 2. Aqui, consideramos a luz proveniente de diferentes partes da mesma fenda. De acordo com o princípio de Huygens, cada parte da frente de onda na fenda emite ondas. São como raios que começam em fase e se dirigem em todas as direções. (Cada raio é perpendicular à frente de onda de uma wavelet.) Supondo que a tela esteja muito distante em comparação com o tamanho da fenda, os raios que se dirigem para um destino comum são quase paralelos. Quando eles viajam em frente, como na Figura 2a, eles permanecem em fase e um máximo central é obtido. No entanto, quando os raios viajam em um ângulo em\(\theta\) relação à direção original do feixe, cada um percorre uma distância diferente até um local comum e pode chegar dentro ou fora de fase. Na Figura 2b, o raio da parte inferior percorre uma distância de um comprimento de onda mais\(\lambda\) distante do que o raio da parte superior. Assim, um raio do centro percorre\(\lambda / 2\) uma distância maior do que o da esquerda, chega fora de fase e interfere destrutivamente. Um raio ligeiramente acima do centro e outro ligeiramente acima da parte inferior também se cancelarão. De fato, cada raio da fenda terá outro para interferir destrutivamente, e um mínimo de intensidade ocorrerá nesse ângulo. Haverá outro mínimo no mesmo ângulo à direita da direção de incidência da luz.

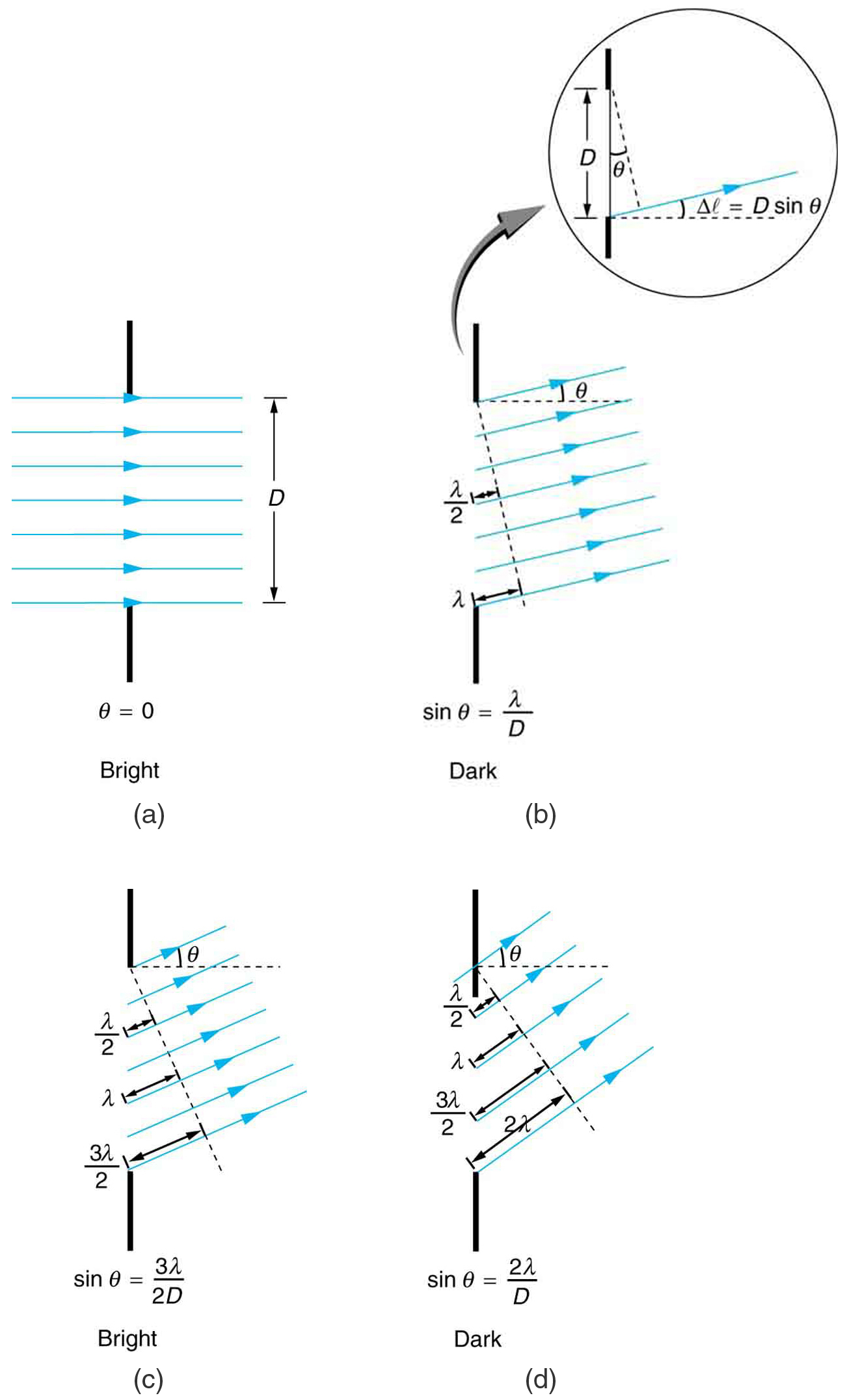
    A figura mostra quatro esquemas de um feixe de raios passando por uma única fenda. A fenda é representada como uma lacuna em uma linha vertical. No primeiro esquema, o feixe de raios passa horizontalmente pela fenda. Esse esquema é rotulado como teta igual a zero e brilhante. O segundo esquema é rotulado como escuro e mostra o feixe de raios passando pela fenda em um ângulo de aproximadamente quinze graus acima da horizontal. A diferença do comprimento do caminho entre o raio superior e inferior é lambda, e o esquema é rotulado como seno teta igual a lambda sobre d. O terceiro esquema é rotulado como brilhante e mostra o feixe de raios passando pela fenda em um ângulo de cerca de vinte e cinco graus acima da horizontal. A diferença do comprimento do caminho entre os raios superior e inferior é de três lambda sobre dois d, e o esquema é rotulado como seno teta igual a três lambda sobre dois d. O esquema final é rotulado como escuro e mostra o feixe de raios passando pela fenda em um ângulo de cerca de quarenta graus acima da horizontal. A diferença do comprimento do caminho entre os raios superior e inferior é de dois lambda sobre d, e o esquema é rotulado como seno teta é igual a dois lambda sobre d.
    Figura\(\PageIndex{2}\): A luz que passa por uma única fenda é difratada em todas as direções e pode interferir de forma construtiva ou destrutiva, dependendo do ângulo. A diferença no comprimento do caminho dos raios de cada lado da fenda é vista como sendo\(D \sin{\theta}\).

    No ângulo maior mostrado na Figura 2c, os comprimentos do caminho diferem em quatro raios da parte superior e inferior da fenda.\(3 \lambda / 2\) Um raio percorre uma distância\(\lambda\) diferente do raio da parte inferior e chega em fase, interferindo de forma construtiva. Dois raios, cada um ligeiramente acima desses dois, também serão adicionados de forma construtiva. A maioria dos raios da fenda terá outro com o qual interferir construtivamente, e uma intensidade máxima ocorrerá nesse ângulo. No entanto, todos os raios não interferem de forma construtiva nessa situação e, portanto, o máximo não é tão intenso quanto o máximo central. Finalmente, na Figura 2d, o ângulo mostrado é grande o suficiente para produzir um segundo mínimo. Como visto na figura, a diferença no comprimento do caminho dos raios de cada lado da fenda é\(D \sin{\theta}\), e vemos que um mínimo destrutivo é obtido quando essa distância é um múltiplo integral do comprimento de onda.

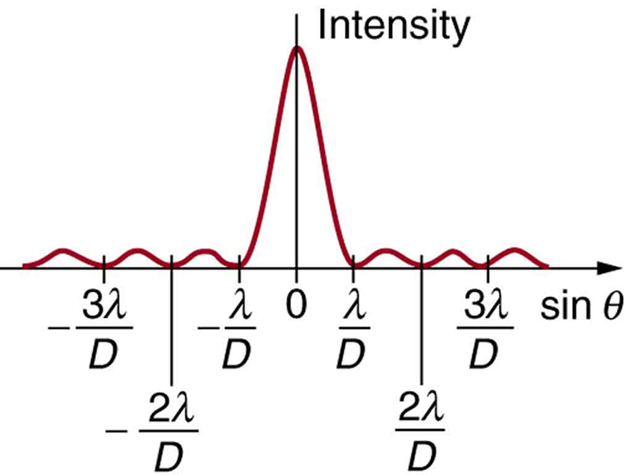
    O gráfico mostra a variação da intensidade em função do seno teta. A curva tem um pico forte em seno teta igual a zero, então tem pequenas oscilações se espalhando simetricamente para a esquerda e para a direita desse pico central. Todas as oscilações parecem ter a mesma altura. Entre cada oscilação, a curva parece ir para zero e cada zero é rotulado. O primeiro zero à esquerda do pico principal é rotulado menos lambda sobre d e o primeiro zero à direita é rotulado como lambda sobre d. O segundo zero à esquerda é rotulado menos dois lambda sobre d e o segundo zero à direita é rotulado como dois lambda sobre d. O terceiro zero à esquerda é rotulado menos três lambda sobre d e o terceiro zero à direita é rotulado como três lambda sobre d.
    Figura\(\PageIndex{3}\): Um gráfico da intensidade de difração de fenda única mostrando que o máximo central é mais largo e muito mais intenso do que aqueles nas laterais. Na verdade, o máximo central é seis vezes maior do que o mostrado aqui.

    Assim, obter interferência destrutiva para uma única fenda,\[D \sin{\theta} = m \lambda,~for~m = 1, -1, 2, -2, 3,... \left(destructive\right), \label{27.6.1}\] onde\(D\) está a largura da fenda,\(\lambda\) é o comprimento de onda da luz,\(\theta\) é o ângulo em relação à direção original da luz e\(m\) é a ordem do mínimo. A Figura 3 mostra um gráfico de intensidade para interferência de fenda única, e é evidente que os máximos em ambos os lados do máximo central são muito menos intensos e não tão largos. Isso é consistente com a ilustração na Figura 1b.

    Exemplo\(\PageIndex{1}\): Calculating Single Slit Diffraction

    A luz visível de comprimento de onda 550 nm cai em uma única fenda e produz sua segunda difração mínima em um ângulo em\(45.0^{\circ}\) relação à direção incidente da luz.

    1. Qual é a largura da fenda?
    2. Em que ângulo o primeiro mínimo é produzido?
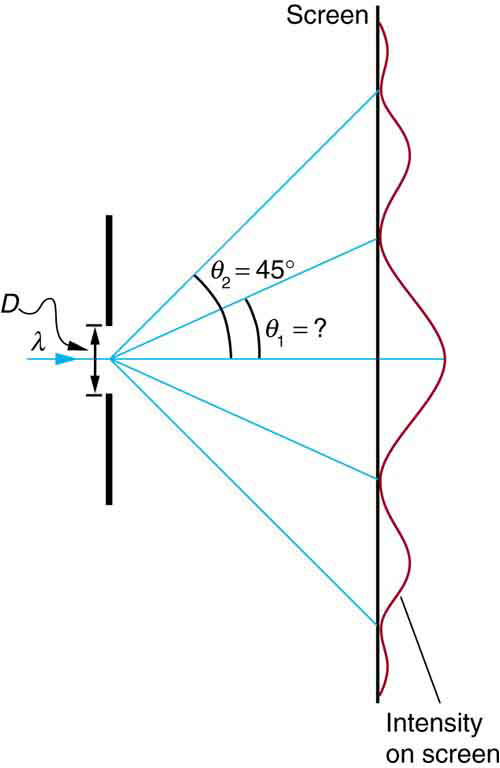
    O esquema mostra uma única fenda à esquerda e o padrão de intensidade resultante em uma tela é representado graficamente à direita. A fenda única é representada por uma lacuna de tamanho d em uma linha vertical. Um raio lambda de comprimento de onda entra na lacuna pela esquerda, depois cinco raios saem do centro da lacuna e vão para a direita. Um raio continua na linha central horizontal do esquema. Dois raios inclinados para cima: o primeiro em um ângulo desconhecido teta um acima da horizontal e o segundo em um ângulo teta dois é igual a quarenta e cinco graus acima da horizontal. Os dois raios finais se inclinam para baixo nos mesmos ângulos, de modo que eles são simétricos em relação à horizontal em relação aos dois raios que se inclinam para cima. A intensidade na tela é máxima onde o raio central atinge a tela, enquanto é mínima quando os raios angulares atingem a tela.
    Figura\(\PageIndex{4}\): Um gráfico do padrão de difração de fenda única é analisado neste exemplo.

    Estratégia:

    A partir das informações fornecidas, e assumindo que a tela está longe da fenda, podemos usar a equação\(D \sin{\theta} = m \lambda\) primeiro para encontrar\(D\) e novamente para encontrar o ângulo do primeiro mínimo\(\theta_{1}\).

    Solução (a):

    Recebemos isso\(\lambda = 550 nm\)\(m =2\),\(\theta_{2} = 45.0^{\circ}\) e. Resolver a equação\(D = \sin{\theta} = m \lambda\)\(D\) e substituir valores conhecidos dá\[D = \frac{m \lambda}{\sin{\theta_{2}}} = \frac{2\left(550 nm\right)}{\sin{45.0^{\circ}}} \label{27.6.2}\]\[= \frac{1100 \times 10^{-9}}{0.707}\]\[=1.56 \times 10^{-6}.\]

    Solução (b):

    Resolver a\(D = \sin{\theta} = m \lambda\) equação\(\sin{\theta_{1}}\) e substituir valores conhecidos dá\[\sin_{\theta_{1}} = \frac{m \lambda}{D} = \frac{1 \left(550 \times 10^{-9} m \right)}{1.56 \times 10^{-6}}. \label{27.6.3}\] Assim, o ângulo\(\theta_{1}\) é\[\theta_{1} = \sin{0.354}^{-1} = 20.7^{\circ} \label{27.6.4}\]

    Discussão:

    Vemos que a fenda é estreita (é apenas algumas vezes maior que o comprimento de onda da luz). Isso é consistente com o fato de que a luz deve interagir com um objeto de tamanho comparável ao seu comprimento de onda para exibir efeitos de onda significativos, como esse padrão de difração de fenda única. Também vemos que o máximo central se estende\(20.7^{\circ}\) em ambos os lados da viga original, por uma largura de cerca de\(41^{\circ}\). O ângulo entre o primeiro e o segundo mínimo é apenas cerca de\(24^{\circ} \left(45.0^{\circ} - 20.7^{\circ}\right)\). Assim, o segundo máximo é apenas cerca de metade da largura do máximo central.

    Resumo

    • Uma única fenda produz um padrão de interferência caracterizado por um amplo máximo central com máximos mais estreitos e mais escuros nas laterais.
    • Há interferência destrutiva para uma única fenda quando\(D \sin{\theta} = m \lambda,~ \left(for~m = 1, -1, 2, -2, 3, ...\right)\) onde\(D\) está a largura da fenda,\(\lambda\) é o comprimento de onda da luz,\(\theta\) é o ângulo em relação à direção original da luz e\(m\) é a ordem do mínimo. Observe que não há um\(m = 0\) mínimo.

    Glossário

    interferência destrutiva para uma única fenda
    ocorre quando\(D \sin{\theta} = m \lambda, \left(for~m = 1, -1, 2, -2, 3, ...\right)\), onde\(D\) está a largura da fenda,\(\lambda\) é o comprimento de onda da luz,\(\theta\) é o ângulo em relação à direção original da luz e\(m\) é a ordem do mínimo