27.4: Difração de fenda múltipla

Last updated
Save as PDF

Page ID: 194397

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Discuta o padrão obtido da grade de difração.
Explique os efeitos da grade de difração.

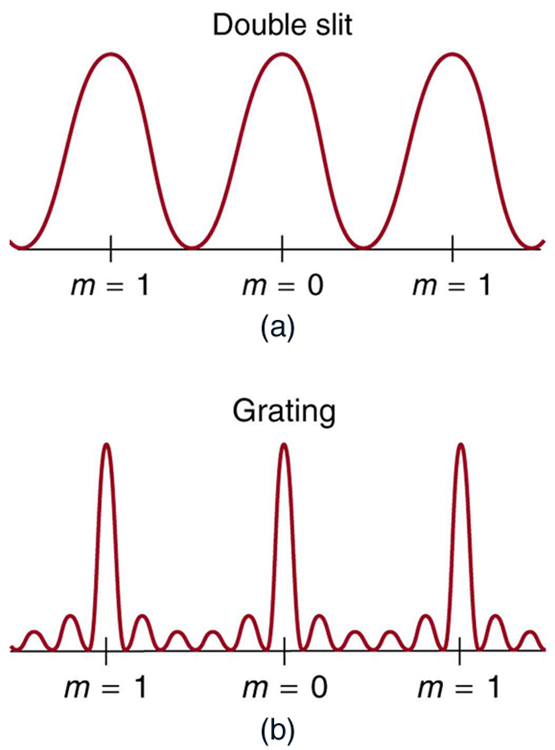
Uma coisa interessante acontece se você passar a luz por um grande número de fendas paralelas uniformemente espaçadas, chamadas de grade de difração. É criado um padrão de interferência muito semelhante ao formado por uma fenda dupla (veja a Figura 1). Uma grade de difração pode ser fabricada riscando o vidro com uma ferramenta afiada em várias linhas paralelas posicionadas com precisão, com as regiões intocadas agindo como fendas. Eles podem ser produzidos fotograficamente em massa de forma bastante barata. As grades de difração funcionam tanto para transmissão de luz, como na Figura 1, quanto para reflexão da luz, como nas asas de borboleta e na opala australiana na Figura 2 ou no CD ilustrado na fotografia de abertura deste capítulo. Além de serem usadas como itens inovadores, as grades de difração são comumente usadas para dispersão espectroscópica e análise de luz. O que os torna particularmente úteis é o fato de formarem um padrão mais nítido do que as fendas duplas. Ou seja, suas regiões claras são cada vez mais estreitas, enquanto suas regiões escuras são mais escuras. A Figura 3 mostra gráficos idealizados demonstrando o padrão mais nítido. Grades de difração natural ocorrem nas penas de certos pássaros. Estruturas minúsculas semelhantes a dedos em padrões regulares atuam como grades de reflexão, produzindo interferências construtivas que dão cores às penas não apenas devido à sua pigmentação. Isso é chamado de iridescência.

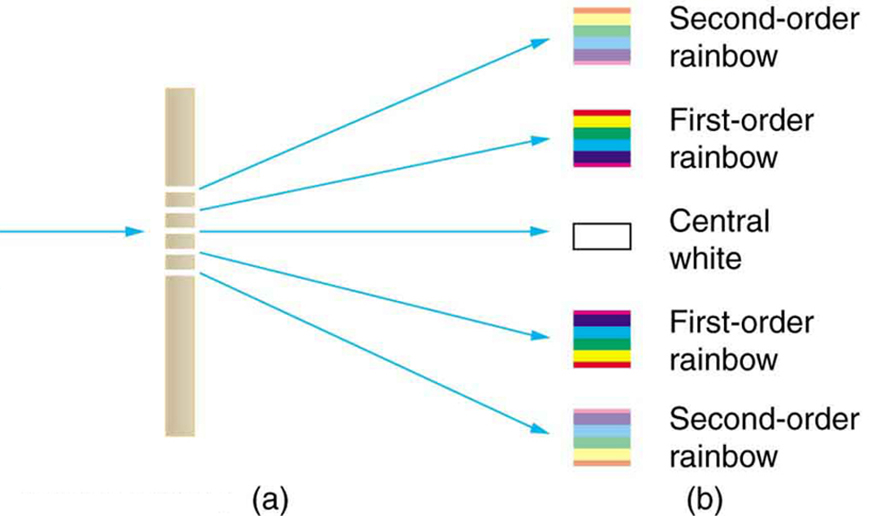
No lado esquerdo da figura está uma grade de difração representada por uma barra vertical com cinco fendas horizontais cortadas nela. Uma única seta horizontal, representando a luz branca, aponta para a fenda central do lado esquerdo. No lado direito, cinco setas se espalham simetricamente acima e abaixo da linha central horizontal. A seta que está na linha central horizontal aponta para um bloco branco rotulado como branco central. As primeiras setas acima e abaixo da linha central apontam para blocos da cor do arco-íris rotulados como arco-íris de primeira ordem. As segundas setas acima e abaixo da linha central apontam para blocos ligeiramente desbotados da cor do arco-íris que são rotulados como arco-íris de segunda ordem. — Figura\(\PageIndex{1}\): Uma grade de difração é um grande número de fendas paralelas espaçadas uniformemente. (a) A luz que passa é difratada em um padrão semelhante a uma fenda dupla, com regiões brilhantes em vários ângulos. (b) O padrão obtido para luz branca incidente em uma grade. O máximo central é branco, e os máximos de ordem superior dispersam a luz branca em um arco-íris de cores.

Fotos coloridas de uma opala australiana e uma borboleta. A opala está cheia de vermelhos e amarelos ardentes e azuis e roxos profundos. A borboleta tem suas asas amarelas abertas e você pode ver suas características manchas e franjas vermelhas, azuis e pretas. — Figura\(\PageIndex{2}\): (a) Esta opala australiana e (b) as asas da borboleta têm fileiras de refletores que agem como grades de reflexão, refletindo cores diferentes em ângulos diferentes. (créditos: (a) Opals-on-Black.com, via Flickr (b) whologwhy, Flickr)

O gráfico superior, chamado de fenda dupla, mostra uma curva suave semelhante a uma curva senoidal que é deslocada para cima de forma que seu valor mínimo seja zero. Três picos são mostrados: o pico médio é rotulado como m igual a zero e os picos esquerdo e direito são rotulados como m igual a um. O gráfico inferior, denominado grade, está alinhado abaixo do gráfico superior e também mostra três picos, com cada pico alinhado diretamente abaixo dos picos no gráfico superior. Esses três picos também são rotulados como m igual a zero ou um, como no gráfico superior. No entanto, os picos no gráfico inferior são muito mais estreitos e há muitos picos pequenos aparecendo entre picos grandes. — Figura\(\PageIndex{3}\): Gráficos idealizados da intensidade da luz passando por uma fenda dupla (a) e uma grade de difração (b) para luz monocromática. Os máximos podem ser produzidos nos mesmos ângulos, mas os da grade de difração são mais estreitos e, portanto, mais nítidos. As máximas ficam mais estreitas e as regiões ficam mais escuras à medida que o número de fendas aumenta.

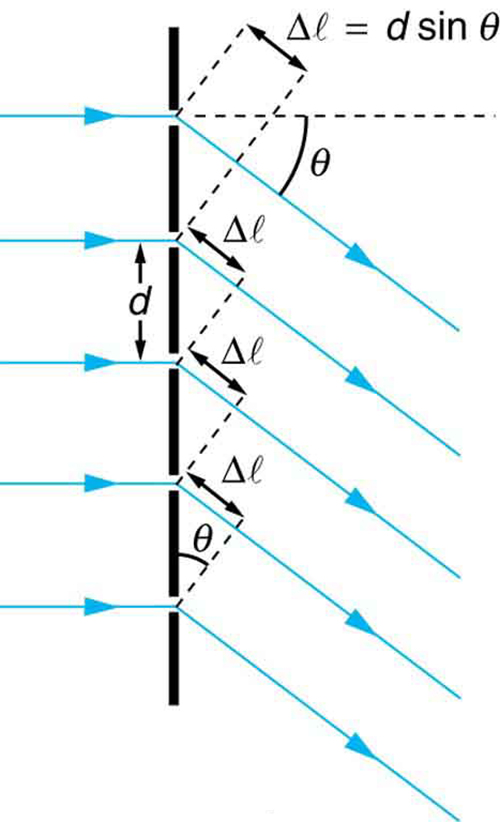
A análise de uma grade de difração é muito semelhante à de uma fenda dupla (veja a Figura 4). Como sabemos em nossa discussão sobre fendas duplas em “Young's Double Slit Experiment”, a luz é difratada por cada fenda e se espalha após a passagem. Os raios viajando na mesma direção (em um ângulo em\(\theta\) relação à direção do incidente) são mostrados na figura. Cada um desses raios percorre uma distância diferente até um ponto comum em uma tela distante. Os raios começam em fase e podem estar dentro ou fora de fase quando chegam a uma tela, dependendo da diferença nos comprimentos do caminho percorrido. Como visto na figura, cada raio percorre uma distância\(d\sin{\theta}\) diferente da de seu vizinho, onde\(d\) está a distância entre as fendas. Se essa distância for igual a um número integral de comprimentos de onda, todos os raios chegarão em fase e a interferência construtiva (um máximo) será obtida. Assim, a condição necessária para obter interferência construtiva para uma grade de difração\(d\) é\[d\sin{\theta} = m \lambda, for m=0,1,-1,2,-2,...\left(constructive\right)\label{27.5.1}\] onde está a distância entre as fendas na grade,\(\lambda\) é o comprimento de onda da luz e\(m\) é a ordem do máximo. Observe que essa é exatamente a mesma equação das fendas duplas separadas por\(d\). No entanto, as fendas geralmente estão mais próximas nas grades de difração do que nas fendas duplas, produzindo menos máximos em ângulos maiores.

A figura mostra um esquema de uma grade de difração, representada por uma linha preta vertical na qual são cortados cinco pequenos espaços. As lacunas são espaçadas uniformemente a uma distância d. Da esquerda chegam cinco raios, com um raio chegando em cada lacuna. À direita da linha com as lacunas, todos os raios apontam para baixo e para a direita em um ângulo teta abaixo da horizontal. Em cada lacuna, um triângulo é formado onde a hipotenusa tem o comprimento d, um ângulo é teta e o lado oposto a teta é rotulado como delta l. Na parte superior está escrito delta l é igual a d seno teta. — Figura\(\PageIndex{4}\): Grade de difração mostrando os raios de luz de cada fenda viajando na mesma direção. Cada raio percorre uma distância diferente para alcançar um ponto comum em uma tela (não mostrado). Cada raio percorre uma distância\(d\sin{\theta}\) diferente da do seu vizinho.

Onde as grades de difração são usadas? As grades de difração são os principais componentes dos monocromadores usados, por exemplo, em imagens ópticas de comprimentos de onda específicos de amostras biológicas ou médicas. Uma grade de difração pode ser escolhida para analisar especificamente um comprimento de onda emitido por moléculas em células doentes em uma amostra de biópsia ou para ajudar a excitar moléculas estratégicas na amostra com uma frequência de luz selecionada. Outro uso vital é em tecnologias de fibra óptica, nas quais as fibras são projetadas para fornecer desempenho ideal em comprimentos de onda específicos. Uma variedade de grades de difração está disponível para selecionar comprimentos de onda específicos para esse uso.

EXPERIÊNCIA PARA LEVAR PARA CASA: ARCO-ÍRIS EM UM CD

O espaçamento\(d\)) das ranhuras em um CD ou DVD pode ser bem determinado usando um laser e a equação.\(d\sin{\theta} = m \lambda, for m = 0,1,-1,2,-2,...\) No entanto, ainda podemos fazer uma boa estimativa desse espaçamento usando luz branca e o arco-íris de cores que vem da interferência. Reflita a luz do sol de um CD na parede e use seu bom senso sobre a localização de uma cor fortemente difratada para encontrar a separação\(d\).

Exemplo\(\PageIndex{1}\): Calculating Typical Diffraction Grating Effects

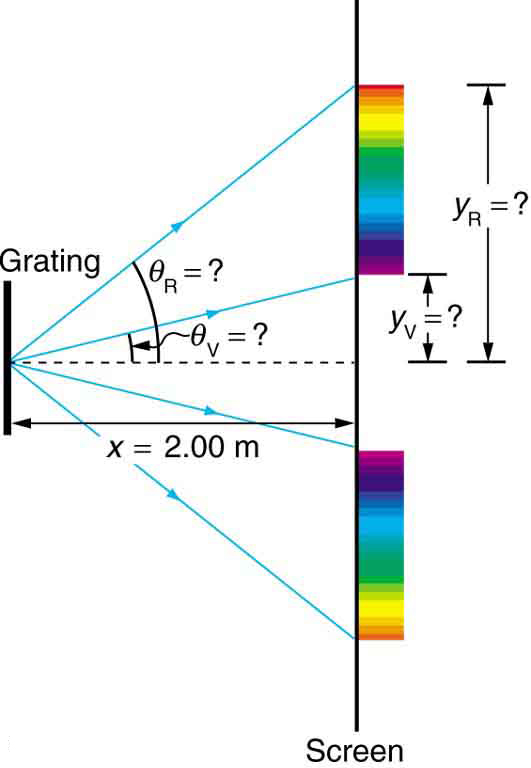
Grades de difração com 10.000 linhas por centímetro estão prontamente disponíveis. Suponha que você tenha um e envie um feixe de luz branca através dele para uma tela a 2,00 m de distância. (a) Encontre os ângulos para a difração de primeira ordem dos comprimentos de onda mais curtos e mais longos da luz visível (380 e 760 nm). (b) Qual é a distância entre as extremidades do arco-íris da luz visível produzida na tela para interferência de primeira ordem? (Veja a Figura.)

A imagem mostra uma barra preta vertical na grade esquerda rotulada. Do ponto médio desta barra, quatro linhas se espalham para a direita, com duas linhas inclinadas acima da linha central horizontal e duas linhas inclinadas simetricamente abaixo da linha central horizontal. Essas quatro linhas atingem uma linha preta vertical à direita que é rotulada como tela. Na tela, entre as duas linhas superiores, há uma região do arco-íris, com violeta mais perto da linha central e vermelho mais longe da linha central. O mesmo vale para as duas linhas inferiores, exceto que elas estão abaixo da linha central em vez de acima. A distância da linha central até a zona violeta superior é rotulada como y sub v é igual ao ponto de interrogação e a distância da linha central até a zona vermelha superior é rotulada como y sub r é igual ao ponto de interrogação. O ângulo entre a linha central e a linha que leva à zona violeta superior é rotulado como teta V é igual ao ponto de interrogação e o ângulo entre a linha que leva à zona vermelha superior é rotulado como teta R igual ao ponto de interrogação. A distância entre a grade e a tela é rotulada como x é igual a dois pontos zero zero metros. — Figura\(\PageIndex{5}\): A grade de difração considerada neste exemplo produz um arco-íris de cores em uma tela a uma\(x = 2.00 m \) distância da grade. As distâncias ao longo da tela são medidas perpendicularmente\(x\) à direção. Em outras palavras, o padrão do arco-íris se estende para fora da página.

Estratégia:

Os ângulos podem ser encontrados usando a equação, uma\[d\sin{\theta} = m \lambda, for m = 0,1,-1,2,-2,...\label{27.5.1}\] vez que um valor para o espaçamento da fenda\(d\) tenha sido determinado. Como existem 10.000 linhas por centímetro, cada linha é separada por\(1/10,000\) de um centímetro. Depois que os ângulos são encontrados, as distâncias ao longo da tela podem ser encontradas usando trigonometria simples.

Solução para (a):

A distância entre as fendas é\(d = \left(1 cm\right) / 10,000 = 1.00 \times 10^{-4} cm\) ou\(1.00 \times 10^{-6} m\). Vamos chamar os dois ângulos\(\theta_{V}\) para violeta (380 nm) e\(\theta_{R}\) vermelho (760 nm). Resolvendo a equação\(d\sin{\theta_{V}} = m \lambda\) para\(\sin{\theta_{V}}\),\[\sin{\theta_{V}} = \frac{m \lambda v}{d}, \label{27.5.2}\] onde\(m = 1\) para primeira ordem\(\lambda_{v} = 380 nm = 3.80 \times 10^{-7} m\) e. Substituindo esses valores, obtém-se,\[\sin{\theta_{v}} = \frac{3.80 \times 10^{-7} m}{1.00 \times 10^{-6} m} = 0.380.\] assim, o ângulo\(\theta_{R}\) é Similar,\[\theta_{v} = \sin^{-1}{0.380} = 22.33^{\circ}.\]\[\sin{\theta_{R}} = \frac{7.60 \times 10^{-7} m}{1.00 \times 10^{-6} m}.\] Assim, o ângulo é\[\theta_{R} = \sin^{-1}{0.760} = 49.46^{\circ}.\] Observe que em ambas as equações, relatamos os resultados desses cálculos intermediários em quatro figuras significativas para usar com o cálculo na parte (b)\(\theta_{v}\) .

Solução para (b):

As distâncias na tela estão rotuladas\(y_{v}\) e\(y_{R}\) na figura. Observando isso\(\tan{\theta} = y/x\), podemos resolver para\(y_{v}\)\(y_{R}\) e. Ou seja,\[y_{v} = x \tan{\theta_{v}} = \left( 2.00 m \right) \left(\tan{22.33^{\circ}}\right) = 0.815m \label{25.7.3}\] e\[y_{R} = x \tan{\theta_{R}} = \left( 2.00 m \right) \left( \tan{49.46^{\circ}} \right) = 2.338 m \label{25.7.4}.\] a distância entre eles é, portanto,\[y_{R} - y_{v} = 1.52 m.\]

Discussão:

A grande distância entre as extremidades vermelha e violeta do arco-íris produzida pela luz branca indica o potencial que essa grade de difração tem como ferramenta espectroscópica. Quanto mais ele pode espalhar os comprimentos de onda (maior dispersão), mais detalhes podem ser vistos em um espectro. Isso depende da qualidade da grade de difração — ela deve ser feita com muita precisão, além de ter linhas bem espaçadas.

Resumo

Uma grade de difração é uma grande coleção de fendas paralelas uniformemente espaçadas que produz um padrão de interferência semelhante, mas mais nítido, do que o de uma fenda dupla.
Há interferência construtiva para uma grade de difração quando\(d\sin{\theta} = m \lambda \left( for m = 0,1,-1,2,-2,...\right)\), onde\(d\) está a distância entre as fendas na grade,\(\lambda\) é o comprimento de onda da luz e\(m\) é a ordem do máximo.

Glossário

interferência construtiva para uma grade de difração: ocorre quando a condição\(d \sin{\theta} = m \lambda \left(for~m = 0,1,-1,2,-2,...\right)\) é satisfeita, onde\(d\) está a distância entre as fendas na grade,\(\lambda\) é o comprimento de onda da luz e\(m\) é a ordem do máximo

grade de difração: um grande número de fendas paralelas espaçadas uniformemente