Skip to main content
Global

26.5: Telescópios

  1. Last updated
  2. Save as PDF
  • Page ID
    194301

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Descreva a invenção de um telescópio.
    • Descreva o funcionamento de um telescópio.

    Os telescópios são destinados à visualização de objetos distantes, produzindo uma imagem maior do que a imagem que pode ser vista a olho nu. Os telescópios coletam muito mais luz do que o olho, permitindo que objetos escuros sejam observados com maior ampliação e melhor resolução. Embora muitas vezes seja creditado a Galileu a invenção do telescópio, ele na verdade não o fez. O que ele fez foi mais importante. Ele construiu vários telescópios antigos, foi o primeiro a estudar os céus com eles e fez descobertas monumentais com eles. Entre elas estão as luas de Júpiter, as crateras e montanhas da Lua, os detalhes das manchas solares e o fato de a Via Láctea ser composta por um grande número de estrelas individuais.

    \(\PageIndex{1a}\)A figura mostra um telescópio feito de duas lentes, a objetiva convexa e a ocular côncava, a mesma construção usada por Galileu. Esse arranjo produz uma imagem vertical e é usado em lunetas e óculos de ópera.

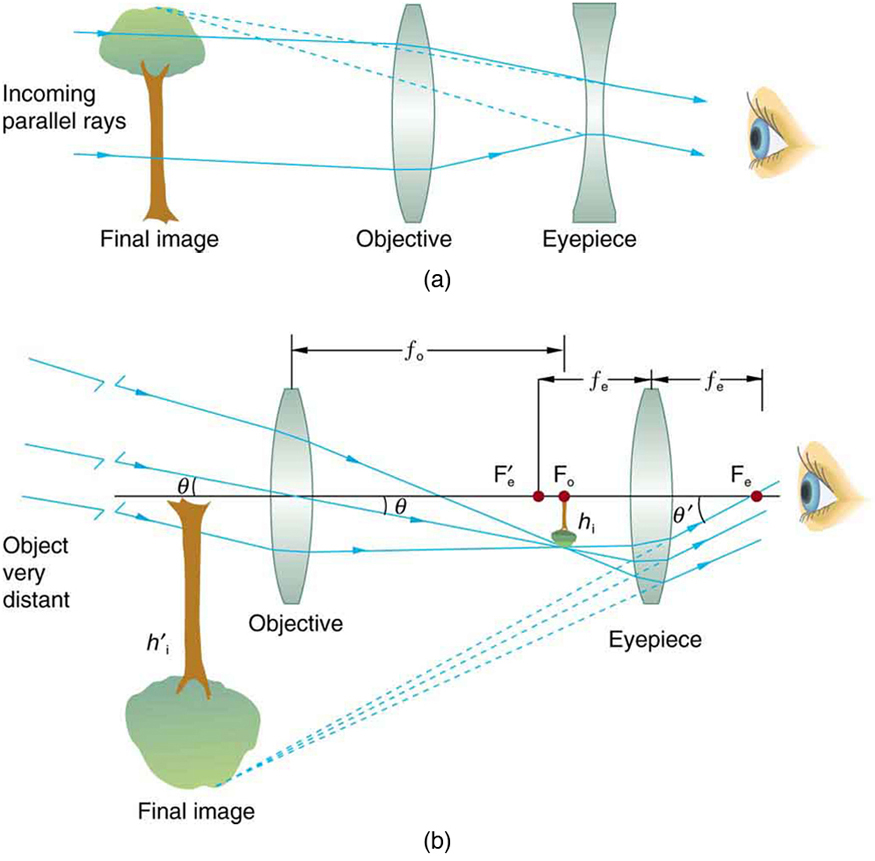
    A parte a da figura mostra o funcionamento interno de um telescópio; da esquerda para a direita, tem uma imagem vertical de uma árvore, uma objetiva de lente convexa, uma lente côncava e uma imagem do olho por onde os raios entram. Raios paralelos atingem a lente convexa objetiva, convergem; atingem a ocular côncava e entram no olho. As linhas pontilhadas dos raios impressionantes da ocular são desenhadas na parte traseira e se unem no início da imagem final. A parte b da figura, da esquerda para a direita, tem uma imagem ampliada invertida de uma árvore, uma objetiva convexa, uma imagem invertida menor de uma árvore, uma ocular convexa e uma imagem de um olho vendo a imagem. Os raios de um objeto muito distante passam pela lente objetiva, focam em um ponto focal f sub o, formando uma imagem menor de cabeça para baixo de uma árvore de altura h sub i, convergem e passam pela ocular para alcançar o olho. Linhas pontilhadas desenhadas para trás focam na ponta da imagem invertida ampliada final de uma árvore de altura h prime sub i, dos raios que atingem a ocular também são mostradas. Um ângulo teta, subtendido pelos raios que atingem a lente objetiva e um ângulo, subtendido pela imagem telescópica ampliada invertida também são representados.
    Figura\(\PageIndex{1}\): (a) Galileu fez telescópios com uma objetiva convexa e uma ocular côncava. Eles produzem uma imagem vertical e são usados em lunetas. (b) A maioria dos telescópios simples tem duas lentes convexas. A objetiva forma uma imagem de caso 1 que é o objeto da ocular. A ocular forma uma imagem final do caso 2 que é ampliada.

    O telescópio de duas lentes mais comum, como o microscópio simples, usa duas lentes convexas e é mostrado na Figura 1b. O objeto está tão distante do telescópio que está essencialmente no infinito em comparação com as distâncias focais das lentes (\(d \approx \infty \)). A primeira imagem é, portanto, produzida em\(d_{i} = f_{o}\), conforme mostrado na figura. Para provar isso, observe que

    \[\frac{1}{d_{i}} = \frac{1}{f_{o}} - \frac{1}{d_{o}} = \frac{1}{f_{o}} - \frac{1}{\infty}.\]

    Porque\(1/\infty = 0\), isso simplifica para

    \[\frac{1}{d_{i}} = \frac{1}{f_{o}},\]

    o que implica isso\(d_{i} = f_{o}\), como alegado. É verdade que para qualquer objeto distante e qualquer lente ou espelho, a imagem está na distância focal.

    A primeira imagem formada por uma objetiva de telescópio, conforme vista na Figura, não\(\PageIndex{1b}\) será grande em comparação com o que você pode ver ao olhar diretamente para o objeto. Por exemplo, a mancha formada pela luz solar focada em um pedaço de papel por uma lupa é a imagem do Sol e é pequena. A ocular do telescópio (como a ocular do microscópio) amplia essa primeira imagem. A distância entre a ocular e a lente objetiva é um pouco menor que a soma de suas distâncias focais, de modo que a primeira imagem fique mais próxima da ocular do que sua distância focal. Ou seja,\(d_{o}'\) é menos isso e\(f_{e}\), portanto, a ocular forma uma imagem do estojo 2 que é grande e à esquerda para facilitar a visualização. Se o ângulo subtendido por um objeto visto a olho nu for\(\theta\), e o ângulo subtendido pela imagem do telescópio for\(\theta '\), então a ampliação angular\(M\) é definida como sua proporção. Isso é,\(M = \theta ' / \theta \). Pode-se mostrar que a ampliação angular de um telescópio está relacionada às distâncias focais da objetiva e da ocular; e é dada por

    \[M = \frac{\theta '}{\theta} = - \frac{f_{o}}{f_{e}}.\label{26.6.1}\]

    O sinal de menos indica que a imagem está invertida. Para obter a maior ampliação angular, é melhor ter uma objetiva de longa distância focal e uma ocular de curta distância focal. Quanto maior a ampliação angular\(M\), maior o objeto aparecerá quando visto por um telescópio, tornando mais detalhes visíveis. Os limites aos detalhes observáveis são impostos por muitos fatores, incluindo a qualidade da lente e a perturbação atmosférica.

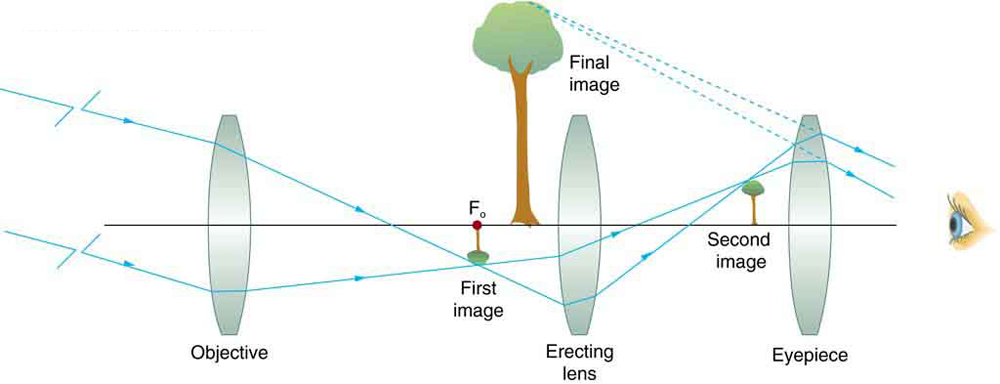
    A imagem na maioria dos telescópios é invertida, o que não é importante para observar as estrelas, mas é um problema real para outras aplicações, como telescópios em navios ou miras telescópicas de canhões. Se for necessária uma imagem vertical, a disposição de Galileo na Figura\(\PageIndex{1a}\) pode ser usada. Mas um arranjo mais comum é usar uma terceira lente convexa como ocular, aumentando a distância entre as duas primeiras e invertendo a imagem novamente, como visto na Figura\(\PageIndex{2}\).

    Um diagrama de raios da esquerda para a direita mostra uma lente objetiva côncava, uma pequena imagem invertida de uma árvore, uma imagem final vertical ampliada da árvore, uma lente côncava ereta, uma pequena imagem vertical de uma árvore, lente côncava como ocular e um olho para ver no mesmo eixo óptico. Os raios de um objeto distante atingem as bordas da lente objetiva, convergem para o foco do ponto focal, formam uma pequena imagem invertida do objeto e passam pela lente ereta, formando novamente a pequena imagem vertical do objeto e, finalmente, os raios passam pela ocular até o olho. Linhas pontilhadas unidas para trás a partir dos raios que atingem a ocular se encontram em um ponto em que a imagem vertical ampliada final do objeto é formada.
    Figura\(\PageIndex{2}\): Esse arranjo de três lentes em um telescópio produz uma imagem final vertical. As duas primeiras lentes estão afastadas o suficiente para que a segunda lente inverta a imagem da primeira mais uma vez. A terceira lente funciona como uma lupa e mantém a imagem na vertical e em um local fácil de visualizar.

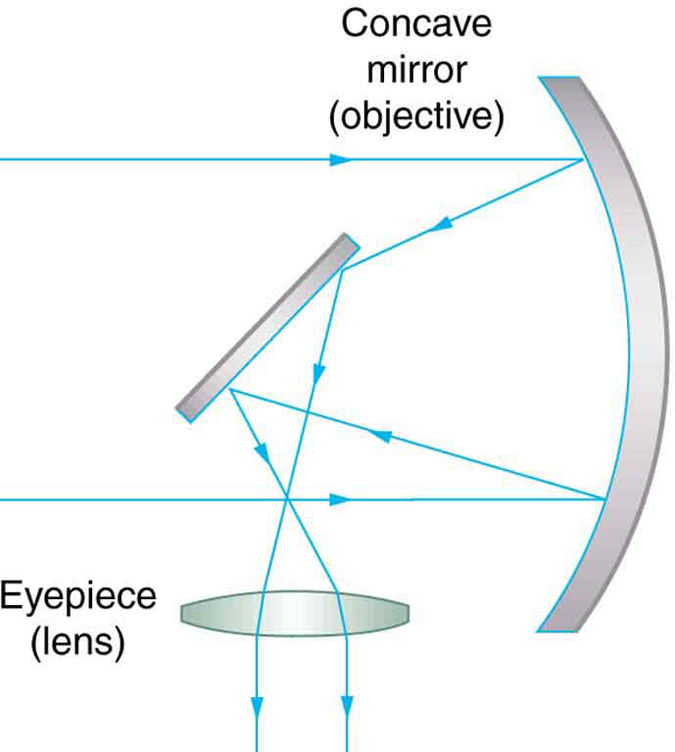
    Um telescópio também pode ser feito com um espelho côncavo como primeiro elemento ou objetivo, já que um espelho côncavo age como uma lente convexa, como visto na Figura\(\PageIndex{3}\). Espelhos planos são frequentemente empregados em instrumentos ópticos para torná-los mais compactos ou para enviar luz para câmeras e outros dispositivos de detecção. Há muitas vantagens em usar espelhos em vez de lentes para objetivas de telescópio. Os espelhos podem ser construídos muito maiores do que as lentes e podem, assim, coletar grandes quantidades de luz, conforme necessário para ver galáxias distantes, por exemplo. Espelhos grandes e relativamente planos têm distâncias focais muito longas, de modo que uma grande ampliação angular é possível.

    Um diagrama de raios da esquerda para a direita mostra um pequeno espelho diagonal e uma ocular de lente côncava posicionada paralelamente uma à outra. Um grande espelho objetivo curvo é colocado na frente do espelho diagonal. Raios de luz paralelos estão caindo nas bordas do espelho objetivo, que é curvado na quantidade certa para refletir toda a luz no espelho diagonal. A partir daí, os raios de luz passam pela lente ocular, que inclina a luz para o olho.
    Figura\(\PageIndex{3}\): Um telescópio de dois elementos composto por um espelho como objetiva e uma lente para a ocular é mostrado. Esse telescópio forma uma imagem da mesma forma que o telescópio de duas lentes convexas já discutido, mas não sofre aberrações cromáticas. Esses telescópios podem captar mais luz, já que espelhos maiores do que lentes podem ser construídos.

    Os telescópios, como os microscópios, podem utilizar uma variedade de frequências do espectro eletromagnético. A Figura 4a mostra o Australia Telescope Compact Array, que usa seis antenas de 22 m para mapear o céu do sul usando ondas de rádio. A figura\(\PageIndex{4b}\) mostra o foco dos raios X no Observatório de Raios X Chandra — um satélite orbitando a Terra desde 1999 e observando eventos de alta temperatura como estrelas explodindo, quasares e buracos negros. Os raios X, com muito mais energia e comprimentos de onda mais curtos do que RF e luz, são absorvidos principalmente e não são refletidos quando incidentes perpendiculares ao meio. Mas eles podem ser refletidos quando incidentes em pequenos ângulos de visão, da mesma forma que uma rocha pulará em um lago se for lançada em um pequeno ângulo. Os espelhos do Chandra consistem em um longo caminho em forma de barril e 4 pares de espelhos para focar os raios em um ponto a 10 metros da entrada. Os espelhos são extremamente lisos e consistem em uma base vitrocerâmica com uma fina camada de metal (irídio). Quatro pares de espelhos fabricados com precisão são primorosamente moldados e alinhados para que os raios X ricocheteiem nos espelhos como balas de uma parede, focando em um ponto.

    A imagem a é uma fotografia de uma das antenas do Australia Telescope Compact Array. A imagem b é um diagrama recortado que mostra 4 conjuntos aninhados de espelhos rígidos de raios-X do observatório de raios-X Chandra.
    Figura\(\PageIndex{4}\): (a) O Australia Telescope Compact Array em Narrabri (500 km a noroeste de Sydney). (crédito: Ian Bailey) (b) O foco dos raios x no Observatório Chandra, um satélite em órbita da Terra. Os raios X ricocheteiam em 4 pares de espelhos formando um caminho em forma de barril que leva ao ponto focal. (crédito: NASA)

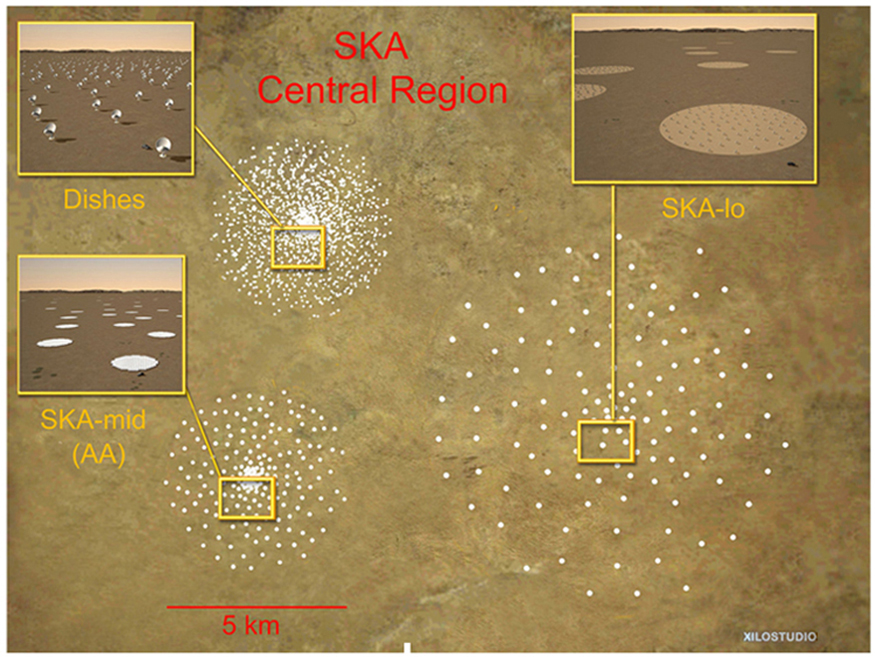
    Um desenvolvimento atual empolgante é um esforço colaborativo envolvendo 17 países para construir uma matriz quadrada de quilômetros (SKA) de telescópios capazes de cobrir de 80 MHz a 2 GHz. A etapa inicial do projeto é a construção do Australian Square Kilometre Array Pathfinder na Austrália Ocidental (veja a Figura 5). O projeto usará tecnologias de ponta, como óptica adaptativa, na qual a lente ou o espelho são construídos a partir de muitas lentes minúsculas e espelhos cuidadosamente alinhados que podem ser manipulados usando computadores. Uma variedade de distorções que mudam rapidamente pode ser minimizada deformando ou inclinando as pequenas lentes e espelhos. O uso da óptica adaptativa na correção da visão é uma área atual de pesquisa.

    Uma visão geral aérea da região central do Square Kilometre Array com os núcleos de cinco quilômetros de diâmetro de antenas ou pratos é vista. A matriz S K A-low e a matriz S K A-mid, que são matrizes em fases de antenas dipolares simples para cobrir a faixa de frequência de setenta a duzentos megahertz e duzentos a quinhentos megahertz em estações circulares, também são exibidas.
    Figura\(\PageIndex{5}\): Uma impressão artística do Australian Square Kilometre Array Pathfinder na Austrália Ocidental é exibida. (crédito: SPDO, XILOSTUDIOS)

    Resumo

    • Telescópios simples podem ser feitos com duas lentes. Eles são usados para visualizar objetos a grandes distâncias e utilizam toda a faixa do espectro eletromagnético.
    • A ampliação angular M para um telescópio é dada por\[M = \frac{\theta '}{\theta} = - \frac{f_{o}}{f_{e}},\] onde\(\theta\) está o ângulo subtendido por um objeto visto a olho nu,\(\theta ' \) é o ângulo subtendido por uma imagem ampliada\(f_{o}\) e\(f_{e}\) são as distâncias focais da objetiva e da ocular.

    Glossário

    óptica adaptativa
    tecnologia óptica na qual os computadores ajustam as lentes e os espelhos em um dispositivo para corrigir distorções na imagem
    ampliação angular
    uma proporção relacionada às distâncias focais da objetiva e da ocular e dada como\(M = - \frac{f_{o}}{f_{e}}\)