26.4: Microscópios

Last updated
Save as PDF

Page ID: 194319

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Investigue diferentes tipos de microscópios.
Saiba como a imagem é formada em um microscópio composto.

Embora o olho seja maravilhoso em sua capacidade de ver objetos grandes e pequenos, ele obviamente tem limitações nos menores detalhes que pode detectar. O desejo humano de ver além do que é possível a olho nu levou ao uso de instrumentos ópticos. Nesta seção, examinaremos microscópios, instrumentos para ampliar os detalhes que não podemos ver a olho nu. O microscópio é um sistema de vários elementos com mais de uma única lente ou espelho (Figura\(\PageIndex{1}\)). Um microscópio pode ser feito de duas lentes convexas. A imagem formada pelo primeiro elemento se torna o objeto do segundo elemento. O segundo elemento forma sua própria imagem, que é o objeto do terceiro elemento, e assim por diante. O traçado de raios ajuda a visualizar a imagem formada. Se o dispositivo for composto por lentes finas e espelhos que obedecem às equações das lentes finas, não é difícil descrever seu comportamento numericamente.

Imagem de um homem vendo através da lente ocular e com a mão no ajuste fino do microscópio. — Figura\(\PageIndex{1}\): Várias lentes e espelhos são usados neste microscópio. (crédito: foto da Marinha dos EUA de Tom Watanabe)

Os microscópios foram desenvolvidos pela primeira vez no início dos anos 1600 por fabricantes de óculos na Holanda e na Dinamarca. O microscópio composto mais simples é construído a partir de duas lentes convexas, conforme mostrado esquematicamente na Figura 2. A primeira lente é chamada de lente objetiva e tem valores de ampliação típicos de\(5 \times\) até\(100 \times\). Em microscópios padrão, as objetivas são montadas de forma que, ao alternar entre as objetivas, a amostra permaneça focada. Os objetivos organizados dessa maneira são descritos como parfocais. A segunda, a ocular, também conhecida como ocular, tem várias lentes que deslizam dentro de um cano cilíndrico. A capacidade de focagem é fornecida pelo movimento da lente objetiva e da ocular. O objetivo de um microscópio é ampliar objetos pequenos, e ambas as lentes contribuem para a ampliação final. Além disso, a imagem final ampliada é produzida em um local distante o suficiente do observador para ser facilmente visualizada, já que o olho não pode focar em objetos ou imagens muito próximas.

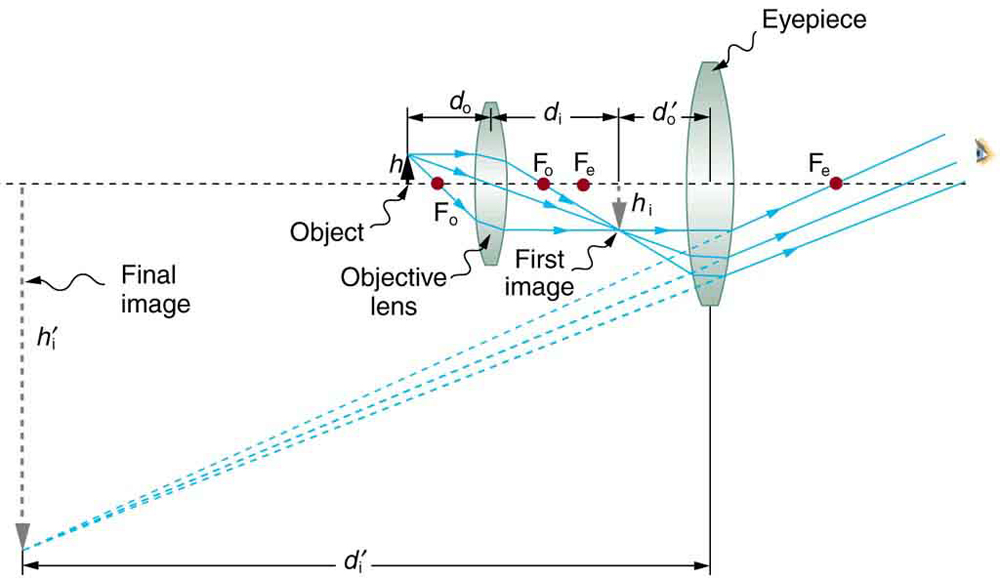
Um diagrama de raios da esquerda para a direita mostra uma imagem final virtual invertida ampliada do objeto, um objeto pequeno na posição vertical, uma lente objetiva convexa, uma imagem menor invertida do objeto, uma ocular grande e convexa e um olho em um eixo óptico. O objeto h' é colocado fora de F subscrito O dois, o foco principal da lente objetiva. Os raios do objeto passam pela lente objetiva, convergindo e formando uma imagem ampliada invertida h subscrito I, que atua como um objeto para a ocular e passa pelo olho. As linhas pontilhadas são unidas para trás a partir dos raios que entram na ocular na ponta da imagem virtual, ampliada, invertida e final do objeto dada como h subscrito i. A distância do objeto para a lente objetiva e a distância da imagem a partir dela são dadas como d subscrito o e d subscrito I, respectivamente. — Figura\(\PageIndex{2}\): Um microscópio composto por duas lentes, uma objetiva e uma ocular. A objetiva forma uma imagem de caso 1 que é maior do que o objeto. Essa primeira imagem é o objeto da ocular. A ocular forma uma imagem final do caso 2 que é ainda mais ampliada.

Para ver como o microscópio na Figura 2 forma uma imagem, consideramos suas duas lentes em sucessão. O objeto está um pouco mais distante da lente objetiva do que sua distância focal\(f_{o}\), produzindo uma imagem de caso 1 maior que o objeto. Essa primeira imagem é o objeto da segunda lente ou ocular. A ocular está localizada intencionalmente para ampliar ainda mais a imagem. A ocular é colocada de forma que a primeira imagem fique mais próxima do que sua distância focal\(f_{e}\). Assim, a ocular atua como uma lupa e a imagem final fica ainda maior. A imagem final permanece invertida, mas está mais distante do observador, facilitando a visualização (o olho fica mais relaxado ao ver objetos distantes e normalmente não consegue focar a menos de 25 cm). Como cada lente produz uma ampliação que multiplica a altura da imagem, é evidente que a ampliação geral\(m\) é o produto das ampliações individuais:\[m = m_{o}m_{e} \label{26.5.1},\] onde\(m_{o}\) está a ampliação da objetiva e\(m_{e}\) a ampliação da ocular. Essa equação pode ser generalizada para qualquer combinação de lentes finas e espelhos que obedeçam às equações de lentes finas.

AMPLIAÇÃO GERAL

A ampliação geral de um sistema de vários elementos é o produto das ampliações individuais de seus elementos.

Exemplo\(\PageIndex{1}\):Microscope Magnification

Calcule a ampliação de um objeto colocado a 6,20 mm a partir de um microscópio composto que tenha uma objetiva de distância focal de 6,00 mm e uma ocular de 50,0 mm de distância focal. A objetiva e a ocular são separadas por 23,0 cm.

Estratégia e conceito:

Essa situação é semelhante à mostrada na Figura 2. Para encontrar a ampliação geral, precisamos encontrar a ampliação da objetiva e, em seguida, a ampliação da ocular. Isso envolve o uso da equação da lente fina.

Solução

A ampliação da lente objetiva é dada como\[m_{o} = -\frac{d_{i}}{d_{o}}\label{26.5.2},\] onde\(d_{o}\) e\(d_{i}\) estão as distâncias do objeto e da imagem, respectivamente, para a lente objetiva, conforme indicado na Figura 2. A distância do objeto é dada como sendo\(d_{o} = 6.20 mm\), mas a distância da imagem não\(d_{i}\) é conhecida. Isolando\(d_{i}\), temos\[\frac{1}{d_{i}} = \frac{1}{f_{o}} - \frac{1}{d_{o}} \label{26.5.3},\] onde\(f_{o}\) está a distância focal da lente objetiva. Substituindo valores conhecidos dá\[\frac{1}{d_{i}} = \frac{1}{6.00 mm} - \frac{1}{6.20 mm} = \frac{0.00538}{mm} .\] Nós invertemos isso para encontrar\(d_{i}\):\[d_{i} = 186 mm.\] Substituindo isso na expressão por\(m_{o}\) dá\[m_{o} = - \frac{d_{i}}{d_{o}} = - \frac{186 mm}{6.20 mm} = -30.0.\] Agora devemos encontrar a ampliação da ocular, que é dada por\[m_{e} = -\frac{d_{i}'}{d_{o}'},\label{26.5.4}\] onde\(d_{i}'\) e\(d_{o}'\) são a imagem e o objeto distâncias para a ocular (veja a Figura 2). A distância do objeto é a distância da primeira imagem da ocular. Como a primeira imagem está 186 mm à direita da objetiva e a ocular está 230 mm à direita da objetiva, a distância do objeto é\(d_{o}' = 230 mm - 186 mm = 44.0 mm\). Isso coloca a primeira imagem mais próxima da ocular do que sua distância focal, de forma que a ocular forme uma imagem de caso 2, conforme mostrado na figura. Ainda precisamos encontrar a localização da imagem\(d_{i}'\) final para encontrar a ampliação. Isso é feito como antes para obter um valor para\(1/d_{i}'\):\[\frac{1}{d_{i}'} = \frac{1}{f_{e}} - \frac{1}{d_{o}'} = \frac{1}{50.0 mm} - \frac{1}{44.0 mm} = - \frac{0.00273}{mm}.\] A inversão dá\[d_{i}' = - \frac{mm}{0.00273} = -367 mm.\] A ampliação da ocular é,\[m_{e} = - \frac{d_{i}'}{d_{o}'} = - \frac{-367 mm}{44.0 mm} = 8.33.\] portanto, a ampliação geral é\[m = m_{o}m_{e} = \left( -30.0 \right) \left( 8.33 \right) = -250.\]

Discussão:

Tanto a objetiva quanto a ocular contribuem para a ampliação geral, que é grande e negativa, consistente com a Figura 2, onde a imagem é vista grande e invertida. Nesse caso, a imagem é virtual e invertida, o que não pode acontecer com um único elemento (as imagens do caso 2 e do caso 3 para elementos únicos são virtuais e verticais). A imagem final está a 367 mm (0,367 m) à esquerda da ocular. Se a ocular tivesse sido colocada mais longe da objetiva, ela poderia ter formado uma imagem de caso 1 à direita. Essa imagem poderia ser projetada em uma tela, mas estaria atrás da cabeça da pessoa na figura e não seria apropriada para visualização direta. O procedimento usado para resolver esse exemplo é aplicável em qualquer sistema de vários elementos. Cada elemento é tratado sucessivamente, com cada um formando uma imagem que se torna o objeto do próximo elemento. O processo não é mais difícil do que para lentes simples ou espelhos, só que mais demorado.

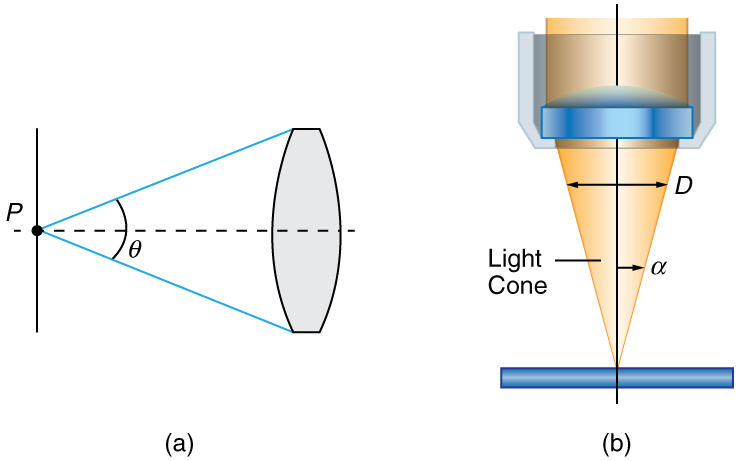
Os microscópios ópticos normais podem ser ampliados até\(1500 \times \) com uma resolução teórica de\(-0.2 \mu m\). As lentes podem ser bastante complicadas e são compostas por vários elementos para reduzir as aberrações. As lentes objetivas do microscópio são particularmente importantes, pois coletam principalmente a luz da amostra. Três parâmetros descrevem as objetivas do microscópio: a abertura numérica (\(NA\)), a ampliação (\(m\)) e a distância de trabalho. O\(NA\) está relacionado à capacidade de coleta de luz de uma lente e é obtido usando o ângulo de aceitação\(\theta\) formado pelo cone máximo de raios focando na amostra (veja a Figura 3a) e é dado por\[NA = n \sin{\alpha} \label{26.5.5},\] onde\(n\) está o índice de refração do meio entre a lente e o espécime\(\alpha = \theta / 2\) e. À medida que o ângulo de aceitação dado pelo\(\theta\) aumenta,\(NA\) se torna maior e mais luz é coletada de uma região focal menor, proporcionando maior resolução. Um\(0.75 NA\) objetivo fornece mais detalhes do que um\(0.10 NA\) objetivo.

A parte a da figura mostra uma linha pontilhada horizontal, um ponto P na linha e uma lente objetiva a uma distância do ponto de forma que um triângulo seja formado do ponto P até as bordas da lente. Um ângulo teta é mostrado no ponto P, representando o cone máximo de raios que entram na lente a partir do ponto P. A parte b da figura mostra os raios de luz de uma amostra entrando na lente de uma câmera mantida acima dela. Os raios formam um cone invertido. — Figura\(\PageIndex{3}\): (a) A abertura numérica (\(NA\)) de uma lente objetiva de microscópio se refere à capacidade de captação de luz da lente e é calculada usando metade do ângulo de aceitação\(\theta\). (b) Aqui,\(\alpha\) está a metade do ângulo de aceitação dos raios de luz de uma amostra que entra na lente da câmera e\(D\) é o diâmetro da abertura que controla a luz que entra na lente.

Embora a abertura numérica possa ser usada para comparar resoluções de várias objetivas, ela não indica a que distância a lente pode estar da amostra. Isso é especificado pela “distância de trabalho”, que é a distância (geralmente em mm) do elemento frontal da lente da objetiva até a amostra, ou vidro de cobertura. Quanto mais alta, mais próxima\(NA\) a lente estará da amostra e maiores serão as chances de quebrar o deslizamento da tampa e danificar a amostra e a lente. A distância focal de uma lente objetiva é diferente da distância de trabalho. Isso ocorre porque as lentes objetivas são feitas de uma combinação de lentes e a distância focal é medida de dentro do cilindro. A distância de trabalho é um parâmetro que os microscopistas podem usar mais facilmente, pois é medida a partir da lente mais externa. A distância de trabalho diminui à medida que a ampliação\(NA\) e a ampliação aumentam.

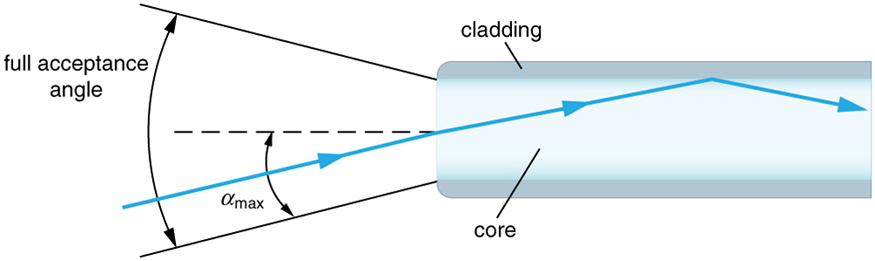
O termo\(f/ \#\) em geral é chamado de\(f\) número -e é usado para denotar a luz por unidade de área que atinge o plano da imagem. Na fotografia, uma imagem de um objeto no infinito é formada no ponto focal e o\(f\) número -é dado pela razão entre a distância focal\(f\) da lente e o diâmetro\(D\) da abertura que controla a luz na lente (veja a Figura 3b). Se o ângulo\(NA\) de aceitação for pequeno, a lente também pode ser usada conforme indicado abaixo. \[f/ \# = \frac{f}{D} \approx \frac{1}{2NA} \label{26.5.6}.\]À medida que o\(f\) número -diminui, a câmera é capaz de captar a luz de um ângulo maior, fornecendo fotografias de grande angular. Como de costume, há uma compensação. Quanto maior\(f/ \#\), menos luz atinge o plano da imagem. Uma configuração de\(f/16\) geralmente permite tirar fotos sob luz solar intensa, pois o diâmetro da abertura é pequeno. Nas fibras ópticas, a luz precisa ser focada na fibra. A Figura 4 mostra o ângulo usado no cálculo\(NA\) de uma fibra óptica.

A imagem de uma fibra óptica multimodo na forma de um retângulo é mostrada. Das bordas, duas linhas divergentes estão saindo, formando o ângulo de aceitação total. Um raio de luz abaixo do eixo óptico está entrando na fibra. Metade do ângulo de aceitação é mostrada como alfa máximo. Dentro da fibra, o raio de luz atinge o revestimento ao redor da fibra e é refletido de volta para a fibra. — Figura\(\PageIndex{4}\): Os raios de luz entram em uma fibra óptica. A abertura numérica da fibra óptica pode ser determinada usando o ângulo\(\alpha_{max}\).

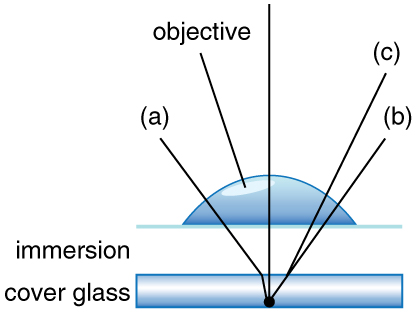
Pode\(NA\) ser maior que 1,00? A resposta é “sim” se usarmos lentes de imersão nas quais um meio como óleo, glicerina ou água é colocado entre a objetiva e a tampa do microscópio. Isso minimiza a incompatibilidade nos índices de refração à medida que os raios de luz passam por diferentes meios, geralmente fornecendo uma maior capacidade de captação de luz e um aumento na resolução. A Figura 5 mostra os raios de luz ao usar lentes de ar e de imersão.

Diagrama dos caminhos da luz de uma amostra e refração no ar, água e óleo. — Figura\(\PageIndex{5}\): Raios de luz de uma amostra entrando na objetiva. Caminhos para o meio de imersão de ar (a), água (b\(n = 1.33\)) () e óleo (c) (\(n = 1.51\)) são mostrados. As imersões em água e óleo permitem que mais raios entrem na objetiva, aumentando a resolução.

Ao usar um microscópio, não vemos toda a extensão da amostra. Dependendo da ocular e da lente objetiva, vemos uma região restrita que dizemos ser o campo de visão. O objetivo é então manipulado em duas dimensões acima da amostra para visualizar outras regiões da amostra. A varredura eletrônica da objetiva ou da amostra é usada na microscopia de varredura. A imagem formada em cada ponto durante a digitalização é combinada usando um computador para gerar uma imagem de uma região maior da amostra em uma ampliação selecionada.

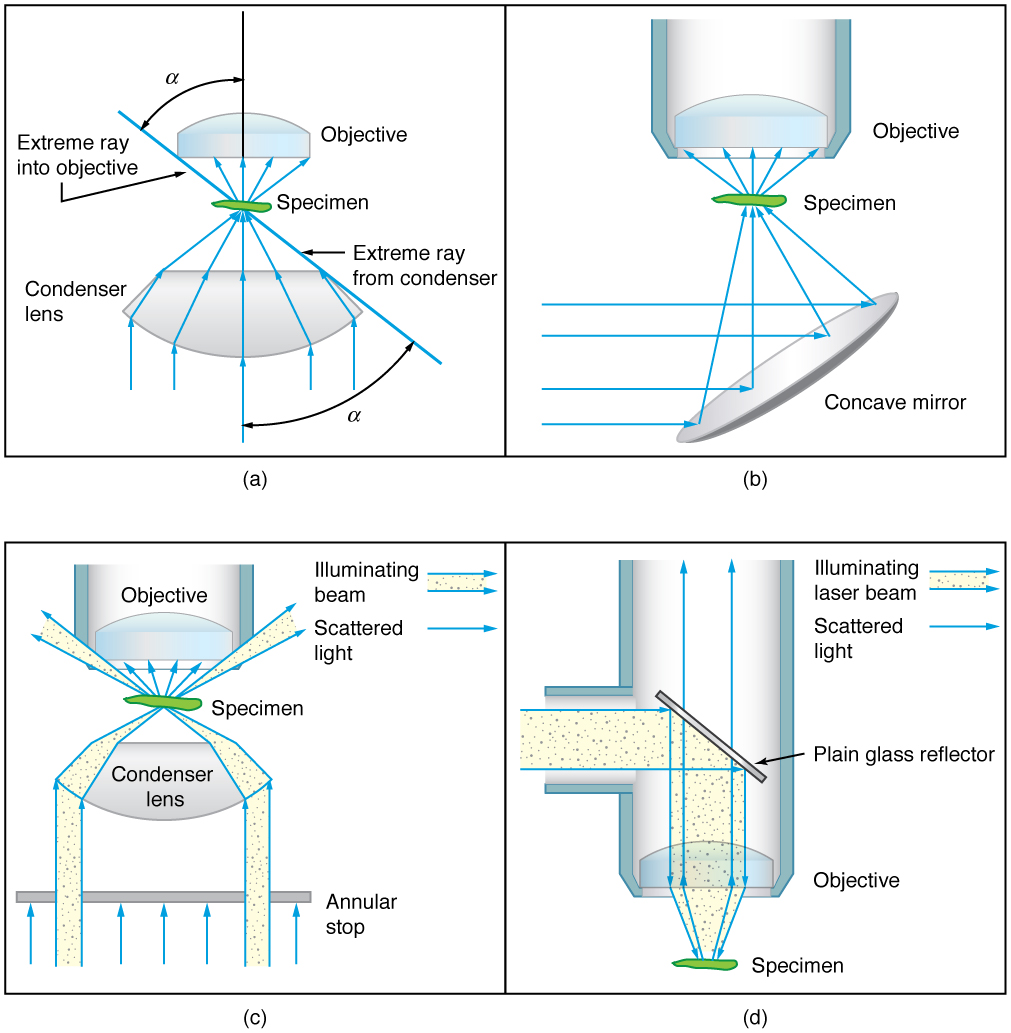
Ao usar um microscópio, contamos com a coleta de luz para formar uma imagem. Portanto, a maioria das amostras precisa ser iluminada, especialmente em ampliações mais altas, ao observar detalhes tão pequenos que refletem apenas pequenas quantidades de luz. Para tornar esses objetos facilmente visíveis, a intensidade da luz que incide sobre eles precisa ser aumentada. Sistemas especiais de iluminação chamados condensadores são usados para essa finalidade. O tipo de condensador adequado para uma aplicação depende de como a amostra é examinada, seja por transmissão, dispersão ou reflexão. Veja a Figura 6 para ver um exemplo de cada um. Fontes de luz branca são comuns e os lasers são frequentemente usados. A iluminação da luz laser tende a ser bastante intensa e é importante garantir que a luz não resulte na degradação da amostra.

Todas as quatro partes mostram diagramas de raios de uma amostra em diferentes tipos de microscópios. A parte a mostra um diagrama de raios com raios através de uma lente condensadora até o objeto e depois até a lente objetiva do microscópio. A parte b mostra um arranjo alternativo em que os raios de luz são refletidos de um espelho condensador côncavo para a amostra e, em seguida, até a lente objetiva do microscópio. A parte c mostra a iluminação do campo escuro, onde o feixe de luz iluminante é fragmentado por um batente anular, de forma que seus raios passem apenas pela parte externa da lente do condensador, o que faz com que eles percam a lente objetiva. A parte d mostra a iluminação de alta ampliação, onde os raios de luz de um laser são refletidos por um refletor de vidro plano, depois passam pela lente objetiva até a lente e retornam como luz dispersa através da lente objetiva. — Figura\(\PageIndex{6}\): Iluminação de uma amostra em um microscópio. (a) Luz transmitida de uma lente condensadora. (b) Luz transmitida de um condensador espelhado. (c) Iluminação do campo escuro por dispersão (o feixe iluminante perde a lente objetiva). (d) Iluminação de alta ampliação com luz refletida — normalmente luz laser.

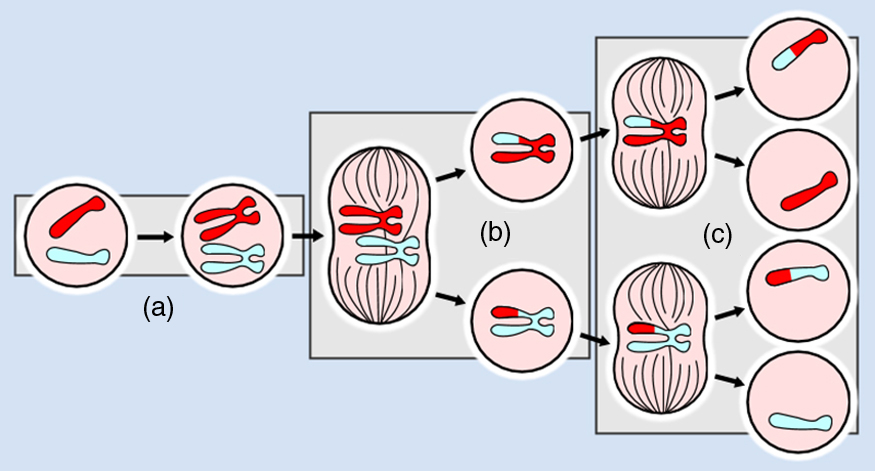
Normalmente associamos microscópios à luz visível, mas microscópios de raios X e eletrônicos fornecem maior resolução. O foco e a física básica são os mesmos que acabamos de descrever, embora as lentes exijam tecnologias diferentes. O microscópio eletrônico requer câmaras de vácuo para que os elétrons possam prosseguir sem serem atendidos. Ampliações de 50 milhões de vezes fornecem a capacidade de determinar as posições de átomos individuais nos materiais. Um microscópio eletrônico é mostrado na Figura 7. Não usamos nossos olhos para formar imagens; em vez disso, as imagens são gravadas eletronicamente e exibidas em computadores. Na verdade, observar e salvar imagens formadas por microscópios ópticos em computadores agora é feito rotineiramente. Gravações de vídeo do que ocorre em um microscópio podem ser feitas para serem vistas por muitas pessoas em datas posteriores. A física fornece a ciência e as ferramentas necessárias para gerar a sequência de imagens de meiose com lapso de tempo semelhante à sequência esboçada na Figura 8.

A imagem mostra um homem usando microscópio eletrônico de varredura. — Figura\(\PageIndex{7}\): Um microscópio eletrônico tem a capacidade de criar imagens de átomos individuais em um material. O microscópio usa tecnologia de vácuo, detectores sofisticados e software de processamento de imagem de última geração. (crédito: Dave Pape)

A figura dá uma visão artística dos diferentes estágios da meiose. — Figura\(\PageIndex{8}\): A imagem mostra uma sequência de eventos que ocorrem durante a meiose. (crédito: PatríciaR, Wikimedia Commons; Centro Nacional de Informações sobre Biotecnologia)

EXPERIÊNCIA PARA LEVAR PARA CASA: FAÇA UMA LENTE

Olhe através de uma garrafa de vidro ou plástico transparente e descreva o que você vê. Agora encha a garrafa com água e descreva o que você vê. Use a garrafa de água como lente para produzir a imagem de um objeto brilhante e estimar a distância focal da lente da garrafa de água. Como a distância focal é função da profundidade da água na garrafa?

Resumo

O microscópio é um sistema de vários elementos com mais de uma única lente ou espelho.
Muitos dispositivos ópticos contêm mais do que uma única lente ou espelho. Eles são analisados considerando cada elemento sequencialmente. A imagem formada pela primeira é o objeto da segunda, e assim por diante. As mesmas técnicas de traçado de raios e lentes finas se aplicam a cada elemento da lente.
A ampliação geral de um sistema de vários elementos é o produto das ampliações de seus elementos individuais. Para um sistema de dois elementos com uma objetiva e uma ocular,\(m_{o}\) é\[m = m_{o}m_{e},\] aqui que está a ampliação da objetiva e\(m_{e}\) a ampliação da ocular, como em um microscópio.
Os microscópios são instrumentos que nos permitem ver detalhes que não conseguiríamos ver a olho nu e consistem em uma variedade de componentes.
A ocular e a objetiva contribuem para a ampliação. A abertura numérica (\(NA\)) de uma objetiva é dada por\[NA = n \sin{\alpha}\] onde\(n\) está o índice de refração e\(\alpha\) o ângulo de aceitação.
As técnicas de imersão são frequentemente usadas para melhorar a capacidade de captação de luz dos microscópios. A amostra é iluminada por luz transmitida, dispersa ou refletida por meio de um condensador.
O\(f / \#\) descreve a capacidade de captação de luz de uma lente. É dado por\[f / \# = \frac{f}{D} \approx \frac{1}{2NA}.\]

Glossário

microscópio composto: um microscópio construído a partir de duas lentes convexas, a primeira servindo como lente ocular (próxima ao olho) e a segunda servindo como lente objetiva

lente objetiva: a lente mais próxima do objeto que está sendo examinado

ocular: a lente ou combinação de lentes em um instrumento óptico mais próximo do olho do observador

abertura numérica: um número ou medida que expressa a capacidade de uma lente de resolver detalhes finos em um objeto que está sendo observado. Derivado pela fórmula matemática,\[NA = n \sin{\alpha},\] onde\(n\) é o índice de refração do meio entre a lente e a amostra e\(\alpha = \theta /2\)