25.E: Óptica geométrica (exercícios)
- Page ID
- 194850
Perguntas conceituais
25.2: A Lei da Reflexão
1. Usando a lei da reflexão, explique como o pó tira o brilho do nariz de uma pessoa. Qual é o nome do efeito óptico?
25.3: A Lei da Refração
2. A difusão por reflexão de uma superfície rugosa é descrita neste capítulo. A luz também pode ser difundida por refração. Descreva como isso ocorre em uma situação específica, como a interação da luz com o gelo picado.
3. Por que o índice de refração é sempre maior ou igual a 1?
4. O fato de o flash da luz chegar até você antes do som prova que a velocidade da luz é extremamente grande ou simplesmente que é maior que a velocidade do som? Discuta como você pode usar esse efeito para obter uma estimativa da velocidade da luz.
5. A luz mudará de direção para ou para longe da perpendicular quando vai do ar para a água? Água para copo? Vidro para o ar?
6. Explique por que um objeto na água sempre parece estar em uma profundidade menor do que realmente é? Por que as pessoas às vezes sofrem lesões no pescoço e na coluna ao mergulhar em lagoas ou águas desconhecidas?
7. Explique por que as pernas de uma pessoa parecem muito curtas ao entrar na piscina. Justifique sua explicação com um diagrama de raios mostrando o caminho dos raios dos pés até o olho de um observador que está fora da água.
8. Por que a superfície frontal de um termômetro é curva conforme mostrado?
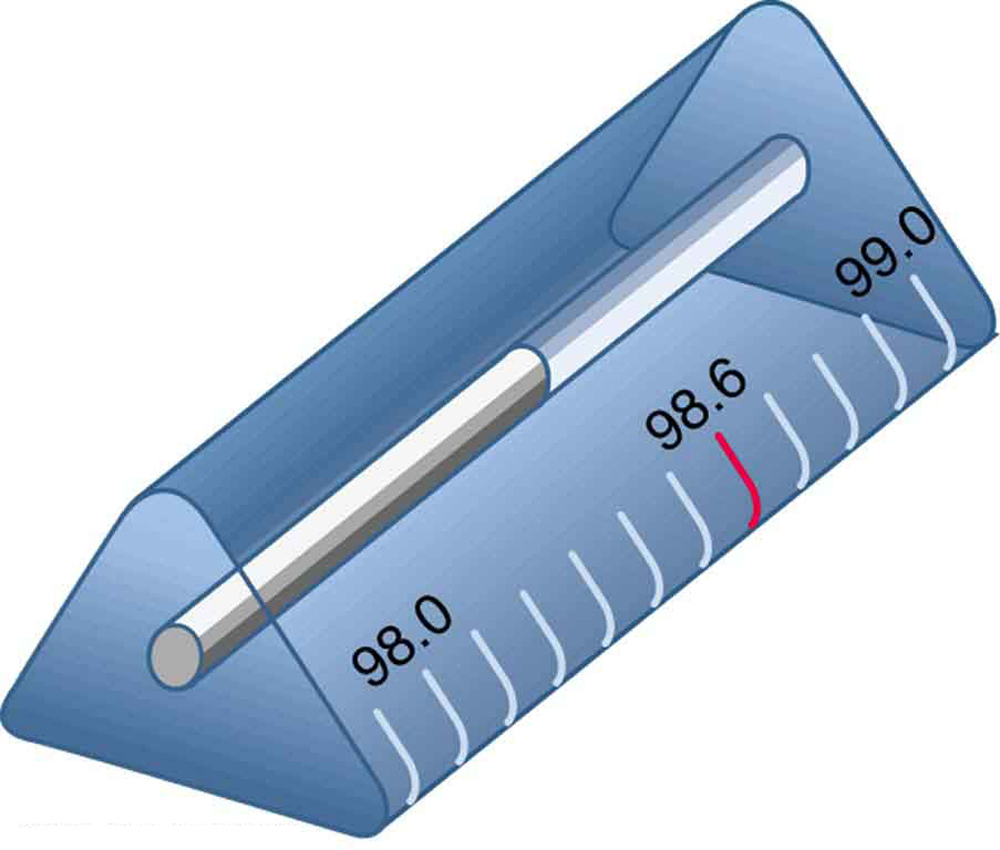
A superfície curva do termômetro serve a um propósito.
9. Suponha que a luz incidisse do ar em um material que tivesse um índice negativo de refração, digamos\(\displaystyle -1.3\); para onde vai o raio de luz refratado?
25.4: Reflexão interna total
10. Um anel com uma pedra preciosa incolor é jogado na água. A pedra preciosa se torna invisível quando submersa. Pode ser um diamante? Explique.
11. Um diamante de alta qualidade pode ser bastante claro e incolor, transmitindo todos os comprimentos de onda visíveis com pouca absorção. Explique como ele pode brilhar com flashes de cores brilhantes quando iluminado por luz branca.
12. É possível que a reflexão interna total desempenhe um papel nos arco-íris? Explique em termos de índices de refração e ângulos, talvez se referindo à figura. Alguns de nós já viram a formação de um arco-íris duplo. É fisicamente possível observar um arco-íris triplo?

Arco-íris duplos não são uma observância muito comum. (crédito: InvictuSou812, Flickr)
13. O tipo mais comum de miragem é a ilusão de que a luz de objetos distantes é refletida por uma piscina de água que não está realmente lá. As miragens geralmente são observadas em desertos, quando há uma camada quente de ar perto do solo. Dado que o índice de refração do ar é menor para o ar em temperaturas mais altas, explique como as miragens podem ser formadas.
25.6: Formação de imagem por lentes
14. Pode-se argumentar que um pedaço de vidro plano, como em uma janela, é como uma lente com uma distância focal infinita. Em caso afirmativo, onde ela forma uma imagem? Ou seja, como estão\(\displaystyle d_{i}\) e se\(\displaystyle d_{o}\) relacionam?
15. Muitas vezes você pode ver um reflexo ao olhar para uma folha de vidro, especialmente se ela estiver mais escura do outro lado. Explique por que muitas vezes você pode ver uma imagem dupla nessas circunstâncias.
16. Ao focalizar uma câmera, você ajusta a distância da lente do filme. Se a lente da câmera funciona como uma lente fina, por que não pode estar a uma distância fixa do filme para objetos próximos e distantes?
17. Uma lente fina tem dois pontos focais, um de cada lado, a distâncias iguais do centro, e deve se comportar da mesma forma com a entrada de luz de ambos os lados. Olhe seus óculos (ou os de um amigo) para trás e para frente e comente se são lentes finas.
18. A distância focal de uma lente mudará quando ela estiver submersa na água? Explique.
25.7: Formação de imagem por espelhos
19. Quais são as diferenças entre imagens reais e virtuais? Como saber (olhando) se uma imagem formada por uma única lente ou espelho é real ou virtual?
20. Você consegue ver uma imagem virtual? Você pode fotografar um? É possível projetar alguém em uma tela com lentes ou espelhos adicionais? Explique suas respostas.
21. É necessário projetar uma imagem real em uma tela para que ela exista?
22. A que distância uma imagem está sempre localizada — em\(\displaystyle d_{o}\)\(\displaystyle d_{i}\), ou\(\displaystyle f\)?
23. Sob quais circunstâncias uma imagem será localizada no ponto focal de uma lente ou espelho?
24. O que se entende por ampliação negativa? O que significa uma ampliação menor que 1 em magnitude?
25. Uma imagem do caso 1 pode ser maior do que o objeto, mesmo que sua ampliação seja sempre negativa? Explique.
26. A figura mostra uma lâmpada entre dois espelhos. Um espelho produz um feixe de luz com raios paralelos; o outro impede que a luz escape sem ser colocada no feixe. Onde está o filamento da luz em relação ao ponto focal ou raio de curvatura de cada espelho?
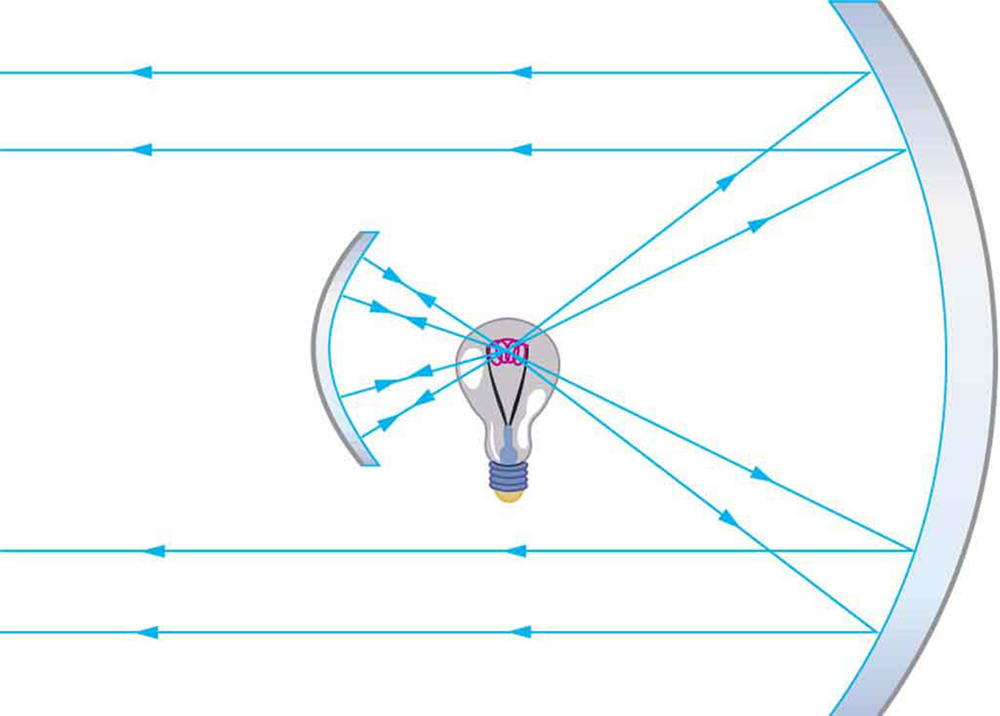
Os dois espelhos capturam a maior parte da luz da lâmpada e formam um feixe direcional como em um farol.
27. Crie um arranjo de espelhos que permita que você veja a nuca. Qual é o número mínimo de espelhos necessários para essa tarefa?
28. Se você deseja ver todo o seu corpo em um espelho plano (da cabeça aos pés), qual deve ter a altura do espelho? Seu tamanho depende da sua distância do espelho? Forneça um esboço.
29. Pode-se argumentar que um espelho plano tem uma distância focal infinita. Em caso afirmativo, onde ela forma uma imagem? Ou seja, como estão\(\displaystyle d_{i}\) e se\(\displaystyle d_{o}\) relacionam?
30. Por que os espelhos divergentes são frequentemente usados para espelhos retrovisores em veículos? Qual é a principal desvantagem de usar esse espelho em comparação com um espelho plano?
Problemas e exercícios
25.1: O aspecto radial da luz
31. Suponha que um homem esteja na frente de um espelho, conforme mostrado na figura. Seus olhos estão 1,65 m acima do chão e o topo da cabeça é 0,13 m mais alto. Encontre a altura acima do chão da parte superior e inferior do menor espelho no qual ele possa ver tanto a parte superior da cabeça quanto os pés. Como essa distância está relacionada à altura do homem?
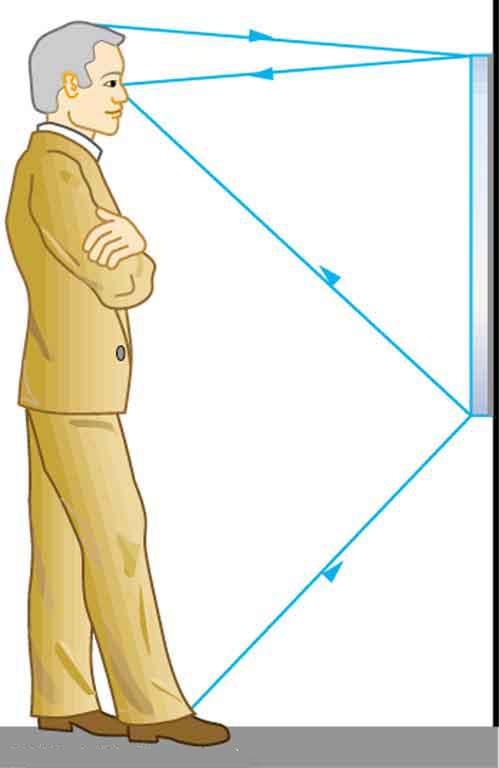
Um espelho de corpo inteiro é aquele em que você pode ver tudo de si mesmo. Não precisa ser tão grande quanto você, e seu tamanho é independente da sua distância.
Solução\(\displaystyle 1.715 m\) de
cima a partir\(\displaystyle 0.825 m\) do chão; de baixo para baixo; altura =\(\displaystyle 0.890 m\), ou exatamente metade da altura da pessoa.
25.2: A Lei da Reflexão
32. Mostre que quando a luz reflete de dois espelhos que se encontram em um ângulo reto, o raio de saída é paralelo ao raio de entrada, conforme ilustrado na figura a seguir.
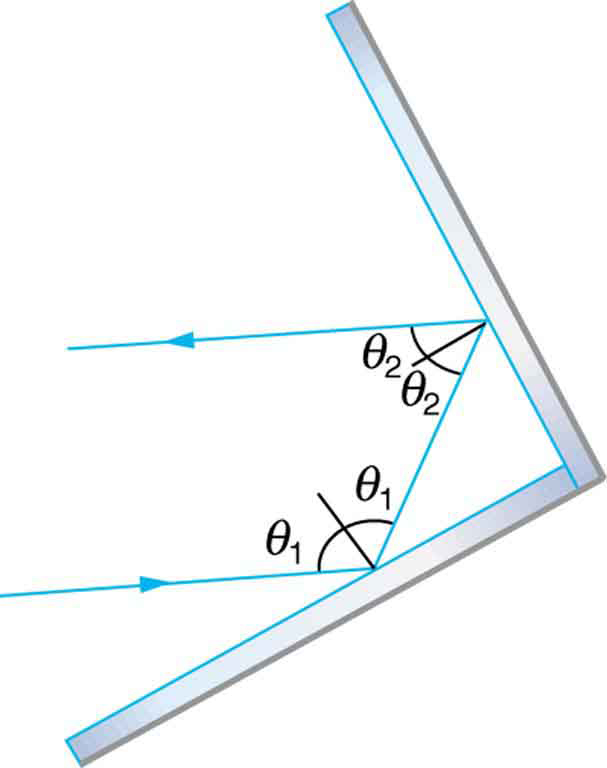
Um refletor de canto envia o raio refletido de volta em uma direção paralela ao raio incidente, independente da direção de entrada.
33. Os shows de luzes encenados com lasers usam espelhos móveis para balançar feixes e criar efeitos coloridos. Mostre que um raio de luz refletido de um espelho muda de direção\(\displaystyle 2\theta\) quando o espelho é girado em um ângulo\(\displaystyle \theta\).
34. Um espelho plano não é convergente nem divergente. Para provar isso, considere dois raios originados do mesmo ponto e divergindo em um ângulo\(\displaystyle \theta\). Mostre que depois de bater em um espelho plano, o ângulo entre suas direções permanece\(\displaystyle \theta\).
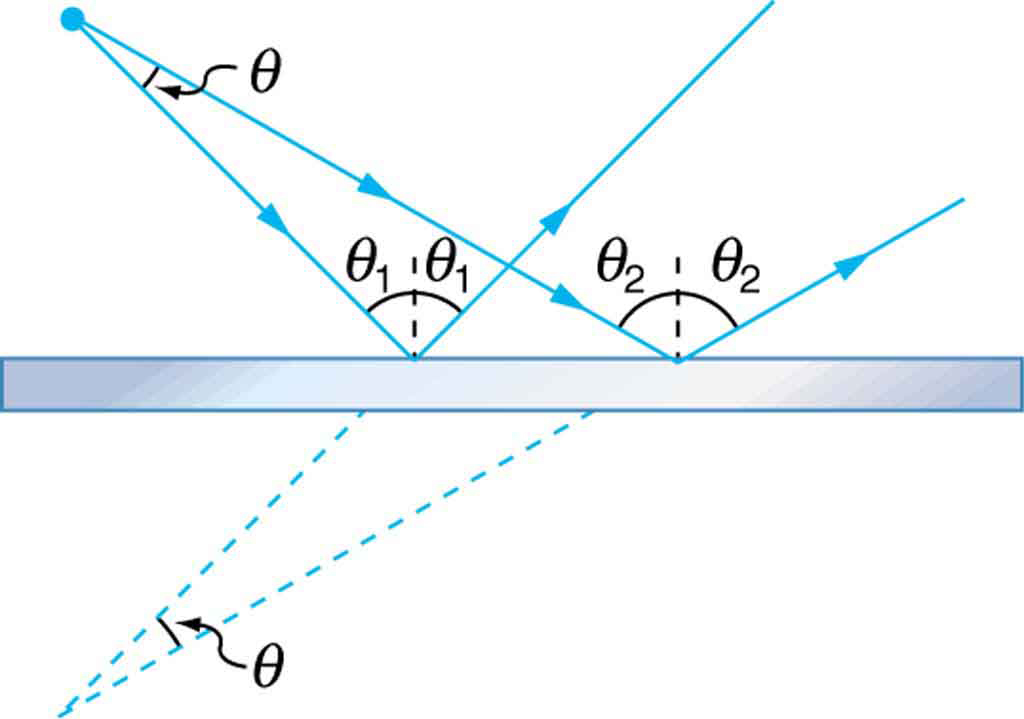
Um espelho plano não converge nem diverge os raios de luz. Dois raios continuam divergindo no mesmo ângulo após a reflexão.
25.3: A Lei da Refração
35. Qual é a velocidade da luz na água? Em glicerina?
Solução
de água —>\(\displaystyle 2.25 \times 10^{8} m/s\)
glicerina —>\(\displaystyle 2.04 \times 10^{8} m/s\)
36. Qual é a velocidade da luz no ar? Em vidro de coroa?
37. Calcule o índice de refração para um meio no qual a velocidade da luz é\(\displaystyle 2.012 \times 10^{8} m/s\) e identifique a substância mais provável com base na tabela.
Solução
\(\displaystyle 1.490\), poliestireno
38. Em que substância na tabela está a velocidade da luz\(\displaystyle 2.290 \times 10^{8} m/s\)?
39. Houve uma grande colisão de um asteróide com a Lua na época medieval. Foi descrito pelos monges da Catedral de Canterbury, na Inglaterra, como um brilho vermelho na Lua e ao redor dela. Quanto tempo depois de o asteroide atingir a Lua, que está\(\displaystyle 3.84 \times 10^{5} km\) ausente, a luz chegaria pela primeira vez à Terra?
Solução
\(\displaystyle 1.28 s\)
40. Um mergulhador treinando em uma piscina olha para seu instrutor conforme mostrado na figura. Qual ângulo o raio do rosto do instrutor faz com a perpendicular à água no ponto em que o raio entra? O ângulo entre o raio na água e a perpendicular à água é\(\displaystyle 25.0^{\circ}\).
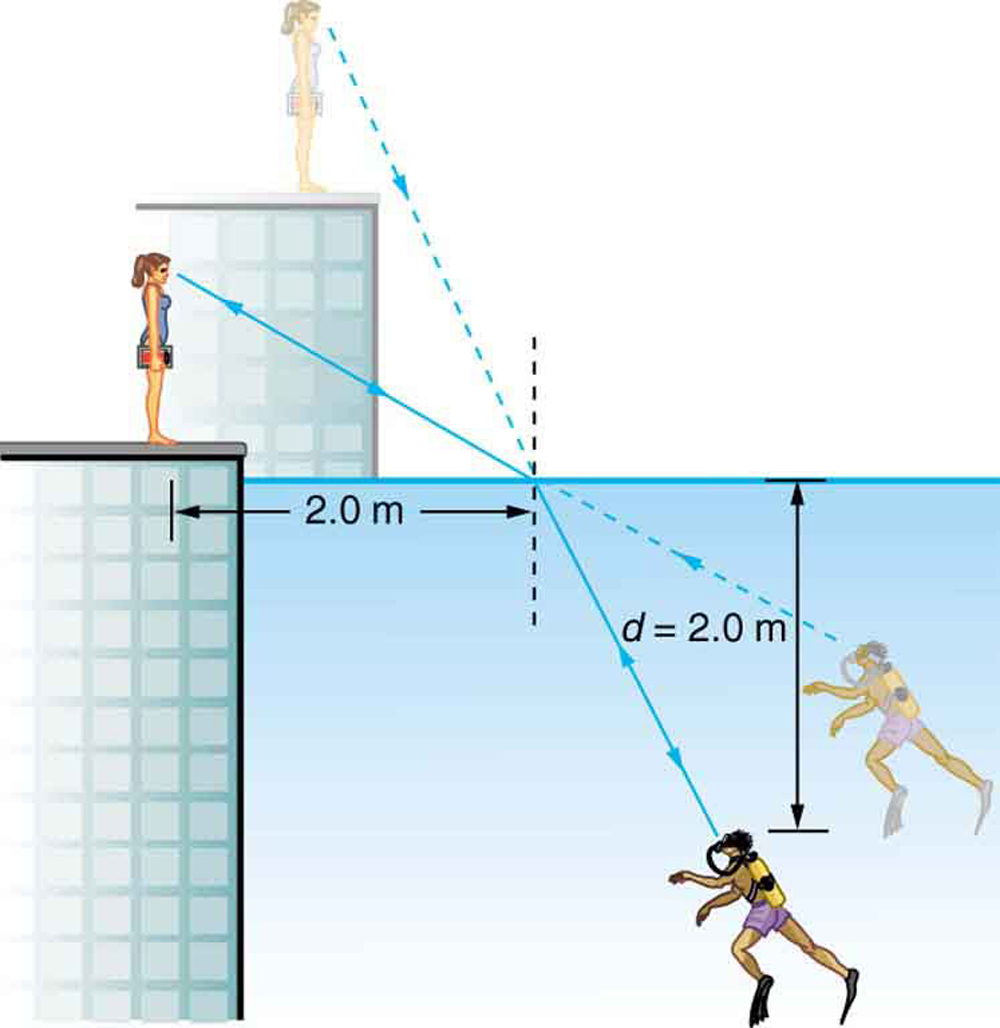
Um mergulhador em uma piscina e seu treinador se entreolham.
41. Os componentes de alguns computadores se comunicam entre si por meio de fibras ópticas com um índice de refração\(\displaystyle n=1.55\). Quanto tempo em nanossegundos é necessário para que um sinal percorra 0,200 m através dessa fibra?
Solução
\(\displaystyle 1.03 ns\)
42. Usando as informações da figura acima,
(a) Dado que o ângulo entre o raio na água e a perpendicular à água é\(\displaystyle 25.0^{\circ}\), encontre a altura da cabeça do instrutor acima da água, observando que primeiro você terá que calcular o ângulo de refração.
(b) encontre a profundidade aparente da cabeça do mergulhador abaixo da água, conforme vista pelo instrutor. Suponha que o mergulhador e a imagem do mergulhador estejam na mesma distância horizontal do normal.
43. Suponha que você tenha uma substância clara desconhecida imersa em água e deseje identificá-la encontrando seu índice de refração. Você faz com que um feixe de luz entre nele em um ângulo de\(\displaystyle 45.0^{\circ}\) e observa que o ângulo de refração é\(\displaystyle 40.3^{\circ}\). Qual é o índice de refração da substância e sua provável identidade?
Solução
\(\displaystyle n = 1.46\), quartzo fundido
44. Na superfície da Lua, os astronautas lunares colocaram um refletor de canto, no qual um feixe de laser é refletido periodicamente. A distância até a Lua é calculada a partir do tempo de ida e volta. Qual porcentagem de correção é necessária para contabilizar o atraso no tempo devido à desaceleração da luz na atmosfera da Terra? Suponha que a distância até a Lua seja precisa\(\displaystyle 3.84 \times 10^{8} m\) e que a atmosfera da Terra (que varia em densidade com a altitude) seja equivalente a uma camada de 30,0 km de espessura com um índice constante de refração\(\displaystyle n = 1.000293\).
45. Suponha que a Figura 6 represente um raio de luz indo do ar através da coroa de vidro para a água, como entrar em um aquário. Calcule a quantidade de deslocamento do raio pelo vidro (\(\displaystyle \Delta x\)), considerando que o ângulo de incidência é\(\displaystyle 40.0^{\circ}\) e o vidro tem 1,00 cm de espessura.
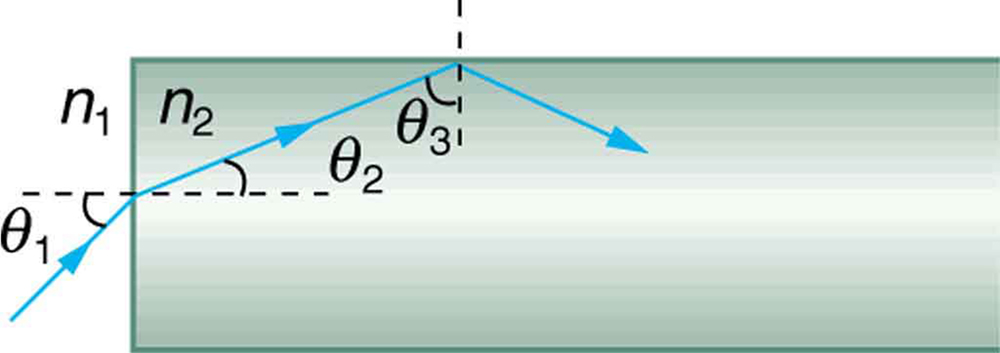
46. A figura mostra um raio de luz passando de um meio para um segundo e depois para um terceiro. Mostre que\(\displaystyle \theta_{3}\) é o mesmo que seria se o segundo meio não estivesse presente (desde que a reflexão interna total não ocorra).
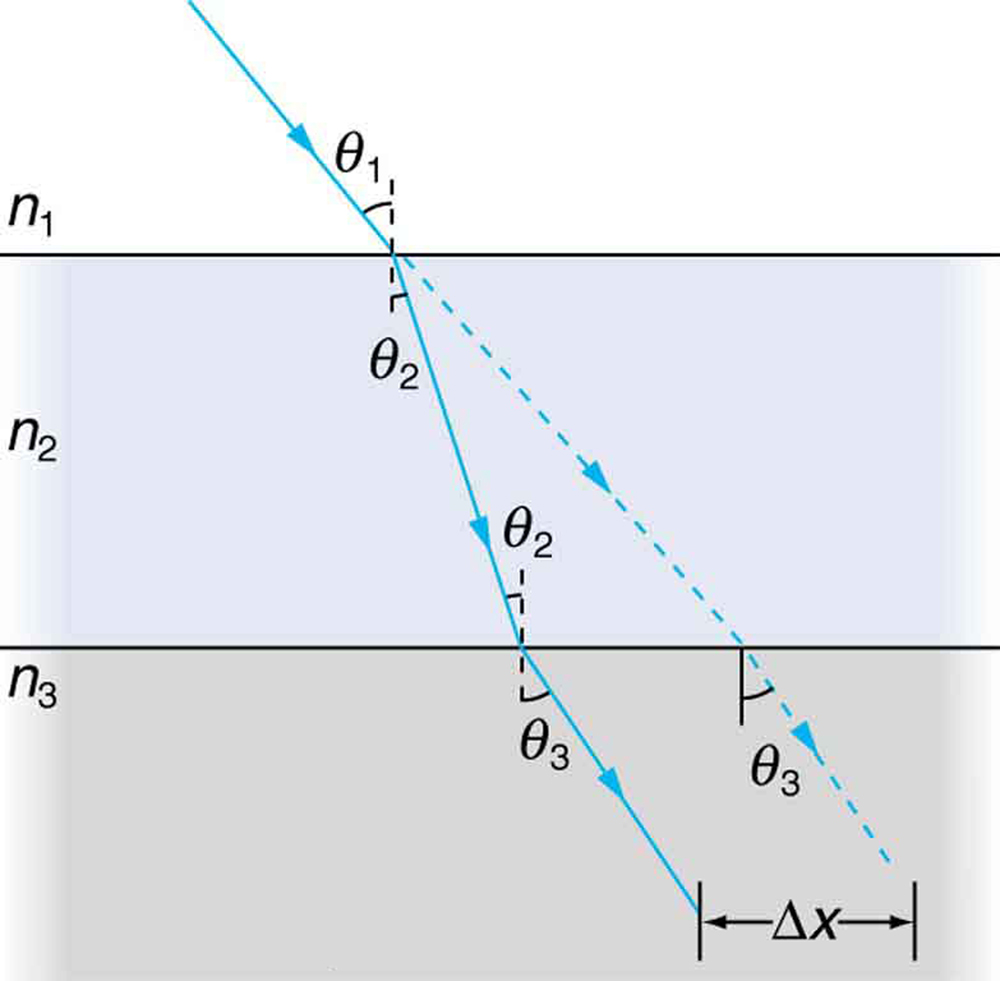
Um raio de luz passa de um meio para um terço viajando por um segundo. A direção final é a mesma de se o segundo meio não estivesse presente, mas o raio está deslocado\(\displaystyle \Delta x\) (mostrado exagerado).
47. Resultados irracionais
Suponha que a luz viaje da água para outra substância, com um ângulo de incidência\(\displaystyle 10.0^{\circ}\) e um ângulo de refração de\(\displaystyle 14.9^{\circ}\).
(a) Qual é o índice de refração da outra substância?
(b) O que não é razoável nesse resultado?
(c) Quais suposições são irracionais ou inconsistentes?
A solução
(a) 0,898
(b) não pode ter,\(\displaystyle n \lt 1.00\) pois isso implicaria que uma velocidade maior que\(\displaystyle c\)
(c) O ângulo refratado é muito grande em relação ao ângulo de incidência.
48. Construa seu próprio problema
Considere a luz do sol entrando na atmosfera da Terra ao nascer e ao pôr do sol, ou seja, em um ângulo de\(\displaystyle 90^{\circ}\) incidência. Considerando que a fronteira entre o espaço quase vazio e a atmosfera é repentina, calcule o ângulo de refração da luz solar. Isso aumenta o tempo em que o Sol parece estar acima do horizonte, tanto ao nascer quanto ao pôr do sol. Agora, construa um problema no qual você determina o ângulo de refração para diferentes modelos da atmosfera, como várias camadas de densidade variável. Talvez seu instrutor queira orientá-lo sobre o nível de complexidade a ser considerado e sobre como o índice de refração varia com a densidade do ar.
49. Resultados irracionais
A luz que viaja da água para uma pedra preciosa atinge a superfície em um ângulo de\(\displaystyle 80.0^{\circ}\) e tem um ângulo de refração de\(\displaystyle 15.2^{\circ}\).
(a) Qual é a velocidade da luz na pedra preciosa?
(b) O que não é razoável nesse resultado?
(c) Quais suposições são irracionais ou inconsistentes?
Solução
(a)\(\displaystyle \frac{c}{5.00}\)
(b) a velocidade da luz muito lenta, uma vez que o índice é muito maior que o do diamante
(c), o ângulo de refração não é razoável em relação ao ângulo de incidência
25.4: Reflexão interna total
50. Verifique se o ângulo crítico da luz que vai da água para o ar é\(\displaystyle 48.6^{\circ}\), conforme discutido no final do exemplo do capítulo, em relação ao ângulo crítico da luz que viaja em um tubo de poliestireno (um tipo de plástico) cercado por ar.
51. (a) No final do exemplo, foi afirmado que o ângulo crítico para a luz que vai do diamante ao ar é\(\displaystyle 24.4^{\circ}\). Verifique isso.
(b) Qual é o ângulo crítico da luz que vai do zircão ao ar?
52. Uma fibra óptica usa vidro de sílex revestido com coroa de vidro. Qual é o ângulo crítico?
Solução
\(\displaystyle 66.3^{\circ}\)
53. Em que ângulo mínimo você obterá a reflexão interna total da luz viajando na água e refletida no gelo?
54. Suponha que você esteja usando a reflexão interna total para criar um refletor de canto eficiente. Se houver ar externo e o ângulo de incidência for,\(\displaystyle 45.0^{\circ}\) qual deve ser o índice mínimo de refração do material do qual o refletor é feito?
Solução
\(\displaystyle \gt 1.414\)
55. Você pode determinar o índice de refração de uma substância determinando seu ângulo crítico.
(a) Qual é o índice de refração de uma substância que tem um ângulo crítico de\(\displaystyle 68.4^{\circ}\) quando submersa na água? Qual é a substância, com base nesse link.
(b) Qual seria o ângulo crítico dessa substância no ar?
56. Um raio de luz, emitido sob a superfície de um líquido desconhecido com ar acima dele, sofre reflexão interna total, conforme mostrado na figura. Qual é o índice de refração do líquido e sua provável identificação?
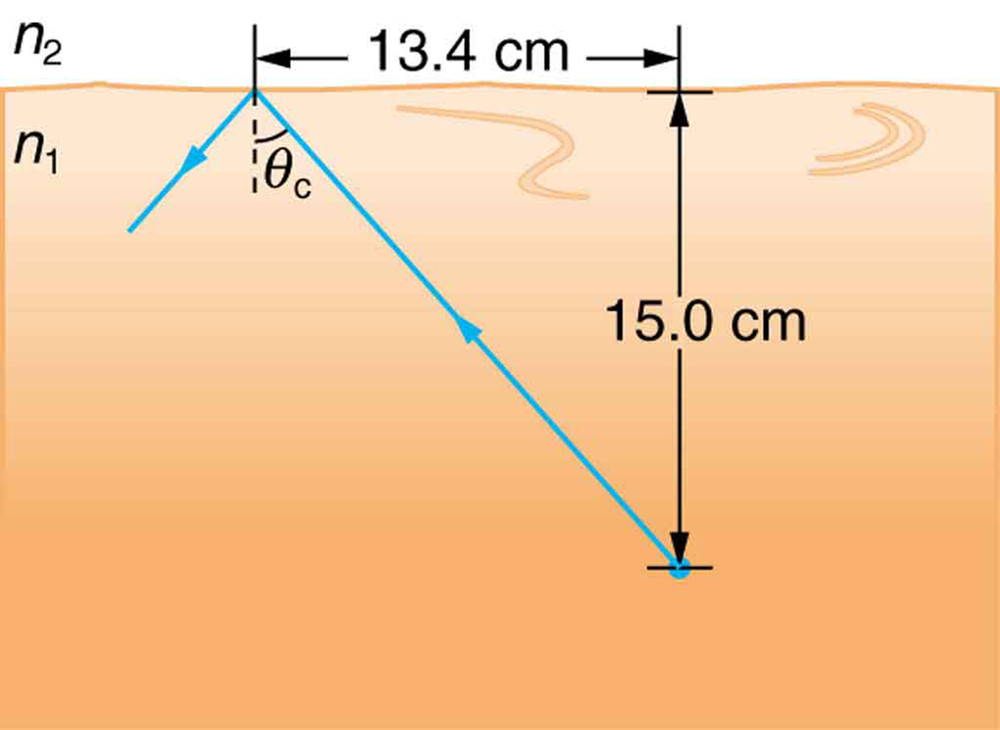
Um raio de luz dentro de um líquido atinge a superfície no ângulo crítico e sofre uma reflexão interna total.
Solução
1,50; benzeno
57. Um raio de luz que entra em uma fibra óptica cercada por ar é primeiro refratado e depois refletido conforme mostrado na figura. Mostre que, se a fibra for feita de coroa de vidro, qualquer raio incidente será totalmente refletido internamente.
Um raio de luz entra na extremidade de uma fibra, cuja superfície é perpendicular aos lados. Examine as condições sob as quais ele pode ser totalmente refletido internamente.
25.5: Dispersão: O arco-íris e os prismas
58. (a) Qual é a relação entre a velocidade da luz vermelha e da luz violeta no diamante, com base na tabela?
(b) Qual é essa proporção em poliestireno?
(c) O que é mais dispersivo?
59. Um feixe de luz branca vai do ar para a água em um ângulo de incidência de\(\displaystyle 75.0^{\circ}\). Em quais ângulos as partes vermelha (660 nm) e violeta (410 nm) da luz são refratadas?
Solução
\(\displaystyle 46.5^{\circ}, red; 46.0^{\circ}, violet\)
60. Em quanto os ângulos críticos da luz vermelha (660 nm) e violeta (410 nm) diferem em um diamante cercado por ar?
61. (a) Um feixe de luz estreito contendo comprimentos de onda amarelos (580 nm) e verdes (550 nm) vai do poliestireno ao ar, atingindo a superfície em um ângulo\(\displaystyle 30.0^{\circ}\) incidente. Qual é o ângulo entre as cores quando elas surgem?
(b) Até onde eles teriam que viajar para serem separados por 1,00 mm?
Solução
(a)\(\displaystyle 0.043^{\circ}\)
(b)\(\displaystyle 1.33 m\)
62. Um feixe de luz paralelo contendo comprimentos de onda laranja (610 nm) e violeta (410 nm) vai do quartzo fundido à água, atingindo a superfície entre eles em um ângulo\(\displaystyle 60.0^{\circ}\) incidente. Qual é o ângulo entre as duas cores na água?
63. Um raio de luz de 610 nm vai do ar para o quartzo fundido em um ângulo de incidência de\(\displaystyle 55.0^{\circ}\) Em que ângulo de incidência a luz de 470 nm deve entrar no vidro de sílex para ter o mesmo ângulo de refração?
Solução
\(\displaystyle 71.3^{\circ}\)
64. Um feixe de luz estreito contendo comprimentos de onda vermelho (660 nm) e azul (470 nm) viaja do ar através de uma peça plana de vidro de 1,00 cm de espessura e volta ao ar novamente. O feixe atinge um ângulo de\(\displaystyle 30.0^{\circ}\) incidência.
(a) Em quais ângulos as duas cores emergem?
(b) A que distância o vermelho e o azul são separados quando emergem?
65. Um feixe estreito de luz branca entra em um prisma feito de coroa de vidro em um ângulo\(\displaystyle 45.0^{\circ}\) incidente, conforme mostrado na figura. Em quais ângulos\(\displaystyle \theta_{R}\) e\(\displaystyle \theta_{V}\), os componentes vermelho (660 nm) e violeta (410 nm) da luz emergem do prisma?
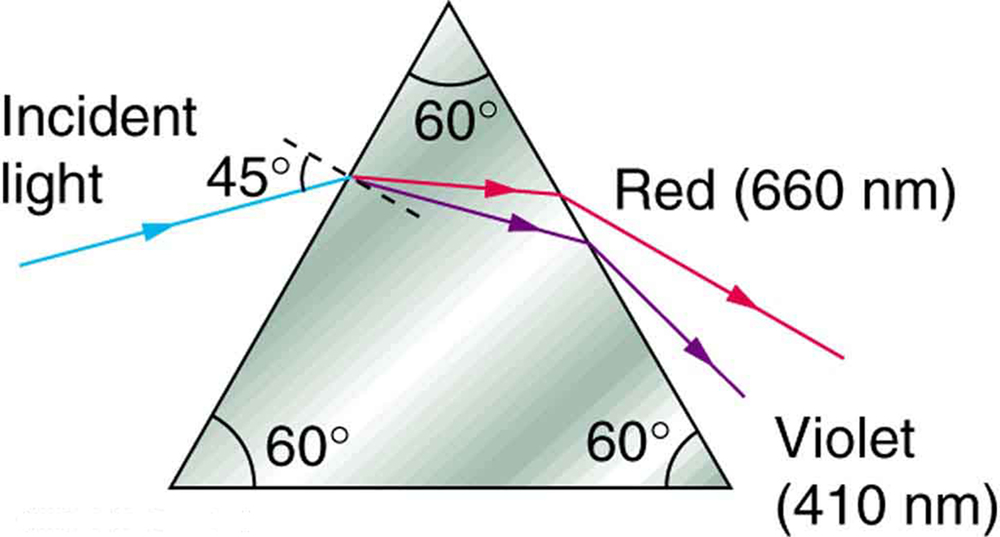
Esse prisma dispersará a luz branca em um arco-íris de cores. O ângulo de incidência é\(\displaystyle 45.0^{\circ}\), e os ângulos em que a luz vermelha e violeta emergem são\(\displaystyle \theta_{R}\)\(\displaystyle \theta_{V}\) e.
Solução
\(\displaystyle 53.5^{\circ}, red; 55.2^{\circ}, violet\)
25.6: Formação de imagem por lentes
66. Qual é a potência em dioptrias de uma lente de câmera que tem uma distância focal de 50,0 mm?
67. A lente de zoom da sua câmera tem uma distância focal ajustável que varia de 80,0 a 200 mm. Qual é a sua gama de poderes?
Solução
\(\displaystyle 5.00 to 12.5 D\)
68. Qual é a distância focal dos óculos de leitura de 1,75 D encontrados na prateleira de uma farmácia?
69. Você observa que sua receita para óculos novos é de —4,50 D. Qual será a distância focal deles?
Solução
\(\displaystyle -0.222 m\)
70. A que distância da lente o filme em uma câmera deve estar, se a lente tiver uma distância focal de 35,0 mm e estiver sendo usada para fotografar uma flor a 75,0 cm de distância? Mostre explicitamente como você segue as etapas da Estratégia de Solução de Problemas para lentes.
71. Um determinado projetor de slides tem uma lente de distância focal de 100 mm.
(a) A que distância fica a tela, se um slide for colocado a 103 mm da lente e produzir uma imagem nítida?
(b) Se o slide tiver 24,0 por 36,0 mm, quais são as dimensões da imagem? Mostre explicitamente como você segue as etapas da Estratégia de Solução de Problemas para lentes.
Solução
(a) 3,43 m
(b) 0,800 por 1,20 m
72. Um médico examina uma toupeira com uma lupa de 15,0 cm de distância focal mantida a 13,5 cm da toupeira
(a) Onde está a imagem?
(b) Qual é sua ampliação?
(c) Qual é o tamanho da imagem de uma toupeira de 5,00 mm de diâmetro?
Solução
(a)\(\displaystyle -1.35 m\) (no lado do objeto da lente)
(b) +10,0
(c) 5,00 cm
73. A que distância de um pedaço de papel você deve segurar os óculos de leitura 2,25 D do seu pai para tentar fazer um buraco no papel com a luz do sol?
Solução
44,4 cm
74. Uma câmera com lente de 50,0 mm de distância focal está sendo usada para fotografar uma pessoa parada a 3,00 m de distância.
(a) A que distância da lente o filme deve estar?
(b) Se o filme tiver 36,0 mm de altura, qual fração de uma pessoa de 1,75 m de altura caberá nele?
(c) Discuta o quão razoável isso parece, com base em sua experiência em tirar ou posar para fotografias.
75. Uma lente de câmera usada para tirar fotografias em close-up tem uma distância focal de 22,0 mm. O mais distante que pode ser colocado do filme é de 33,0 mm.
(a) Qual é o objeto mais próximo que pode ser fotografado?
(b) Qual é a ampliação desse objeto mais próximo?
Solução
(a) 6,60 cm
(b) -0,333
76. Suponha que sua lente de câmera de 50,0 mm de distância focal esteja a 51,0 mm de distância do filme na câmera.
(a) A que distância está um objeto que está em foco?
(b) Qual é a altura do objeto se sua imagem tiver 2,00 cm de altura?
77. (a) Qual é a distância focal de uma lupa que produz uma ampliação de 3,00 quando mantida a 5,00 cm de um objeto, como uma moeda rara?
(b) Calcule a potência da lupa em dioptrias.
(c) Discuta como essa potência se compara às de óculos de leitura comprados em lojas (normalmente 1,0 a 4,0 D). A potência da lupa é maior e deveria ser?
Solução
(a) +7,50 cm
(b) 13,3 D
(c) muito maior
78. Que ampliação será produzida por uma lente de potência de —4,00 D (como a usada para corrigir a miopia) se um objeto for mantido a 25,0 cm de distância?
79. No exemplo “Imagem produzida por uma lupa”, a ampliação de um livro com 7,50 cm de uma lente de distância focal de 10,0 cm foi de 4,00.
(a) Encontre a ampliação do livro quando ele estiver a 8,50 cm da lupa.
(b) Faça o mesmo quando estiver a 9,50 cm da lupa.
(c) Comente sobre a tendência em m à medida que a distância do objeto aumenta, como nesses dois cálculos.
Solução
(a) +6,67
(b) +20,0
(c) A ampliação aumenta sem limite (até o infinito) à medida que a distância do objeto aumenta até o limite da distância focal.
80. Suponha que uma lente telefoto de 200 mm de distância focal esteja sendo usada para fotografar montanhas a 10,0 km de distância. (a) Onde está a imagem? (b) Qual é a altura da imagem de um penhasco de 1000 m de altura em uma das montanhas?
81. Uma câmera com lente de 100 mm de distância focal é usada para fotografar o sol e a lua. Qual é a altura da imagem do sol no filme, dado que o sol tem\(\displaystyle 1.40 \times 10^{6} km\) diâmetro e está\(\displaystyle 1.50 \times 10^{8} km\) distante?
Solução
-0,933 mm
82. Combine equações de lentes finas para mostrar que a ampliação de uma lente fina é determinada pela distância focal e pela distância do objeto e é dada por\(\displaystyle m = f/\left(f - d_{o}\right)\).
25.7: Formação de imagem por espelhos
83. Qual é a distância focal de um espelho de maquiagem com potência de 1,50 D?
Solução
+0,667 m
84. Algumas câmeras teleobjetivas usam um espelho em vez de uma lente. Qual raio de curvatura é necessário para substituir uma lente telefoto de 800 mm de distância focal?
85. (a) Calcule a distância focal do espelho formado pelo dorso brilhante de uma colher com um raio de curvatura de 3,00 cm.
(b) Qual é o seu poder em dioptrias?
Solução
(a)\(\displaystyle -1.5 \times 10^{-2} m\)
(b)\(\displaystyle -66.7 D\)
86. Encontre a ampliação do elemento aquecedor no exemplo do refletor côncavo. Observe que sua grande magnitude ajuda a espalhar a energia refletida.
87. Qual é a distância focal de um espelho de maquiagem que produz uma ampliação de 1,50 quando o rosto de uma pessoa está a 12,0 cm de distância? Mostre explicitamente como você segue as etapas na “Estratégia de solução de problemas para espelhos”.
Solução
+0,360 m (côncava)
88. Um comprador que está a 3,00 m de um espelho de segurança convexo vê sua imagem com uma ampliação de 0,250. (a) Onde está a imagem dele? (b) Qual é a distância focal do espelho? (c) Qual é o seu raio de curvatura? Mostre explicitamente como você segue as etapas na “Estratégia de solução de problemas para espelhos”.
89. Um objeto de 1,50 cm de altura é mantido a 3,00 cm da córnea de uma pessoa e sua imagem refletida é medida em 0,167 cm de altura.
(a) Qual é a ampliação?
(b) Onde está a imagem?
(c) Encontre o raio de curvatura do espelho convexo formado pela córnea. (Observe que essa técnica é usada por optometristas para medir a curvatura da córnea para o encaixe das lentes de contato. O instrumento usado é chamado de ceratômetro ou medidor de curvas.)
Solução
(a) +0,111
(b) -0,334 cm (atrás do “espelho”)
(c) 0,752 cm
90. O traçado de raios para um espelho plano mostra que a imagem está localizada a uma distância atrás do espelho igual à distância do objeto do espelho. Isso é afirmado\(\displaystyle d_{i} = -d_{o}\), pois essa é uma distância negativa da imagem (é uma imagem virtual).
(a) Qual é a distância focal de um espelho plano?
(b) Qual é o seu poder?
91. Mostre isso para um espelho plano\(\displaystyle h_{i} = h_{o}\), sabendo que a imagem está a uma distância atrás do espelho igual em magnitude à distância do objeto do espelho.
Solução
\[m = \frac{h_{i}}{h_{o}} = - \frac{d_{i}}{d_{o}} = - \frac{-d_{o}}{d_{o}} = \frac{d_{o}}{d_{o}} = 1 \rightarrow h_{i} = h_{o}\]
92. Use a lei da reflexão para provar que a distância focal de um espelho é metade do raio de curvatura. Ou seja, prove isso\(\displaystyle f = R/2\). Observe que isso é verdade para um espelho esférico somente se seu diâmetro for pequeno em comparação com seu raio de curvatura.
93. Referindo-se ao aquecedor elétrico de ambiente considerado no primeiro exemplo desta seção, calcule a intensidade da radiação infravermelha\(\displaystyle W/m^{2}\) projetada pelo espelho côncavo em uma pessoa a 3,00 m de distância. Suponha que o elemento de aquecimento irradia 1500 W e tenha uma área de\(\displaystyle 100 cm^{2}\), e que metade da potência irradiada seja refletida e focada pelo espelho.
Solução
\(\displaystyle 6.82 kW/m^{2}\)
94. Considere uma lâmpada de calor de 250 W fixada no teto de um banheiro. Se o filamento de uma luz se queimar, os três restantes ainda funcionarão. Construa um problema no qual você determine a resistência de cada filamento para obter uma certa intensidade projetada no chão do banheiro. O teto tem 3,0 m de altura. O problema precisará envolver espelhos côncavos atrás dos filamentos. Talvez seu instrutor queira orientá-lo sobre o nível de complexidade a ser considerado nos componentes elétricos.


