25.4: Reflexão interna total
- Page ID
- 194918
objetivos de aprendizagem
Ao final desta seção, você poderá:
- Explique o fenômeno da reflexão interna total.
- Descreva o funcionamento e os usos da fibra óptica.
- Analise o motivo do brilho dos diamantes.
Um espelho de boa qualidade pode refletir mais de 90% da luz que incide sobre ele, absorvendo o resto. Mas seria útil ter um espelho que reflita toda a luz que incide sobre ele. Curiosamente, podemos produzir reflexão total usando um aspecto de refração.
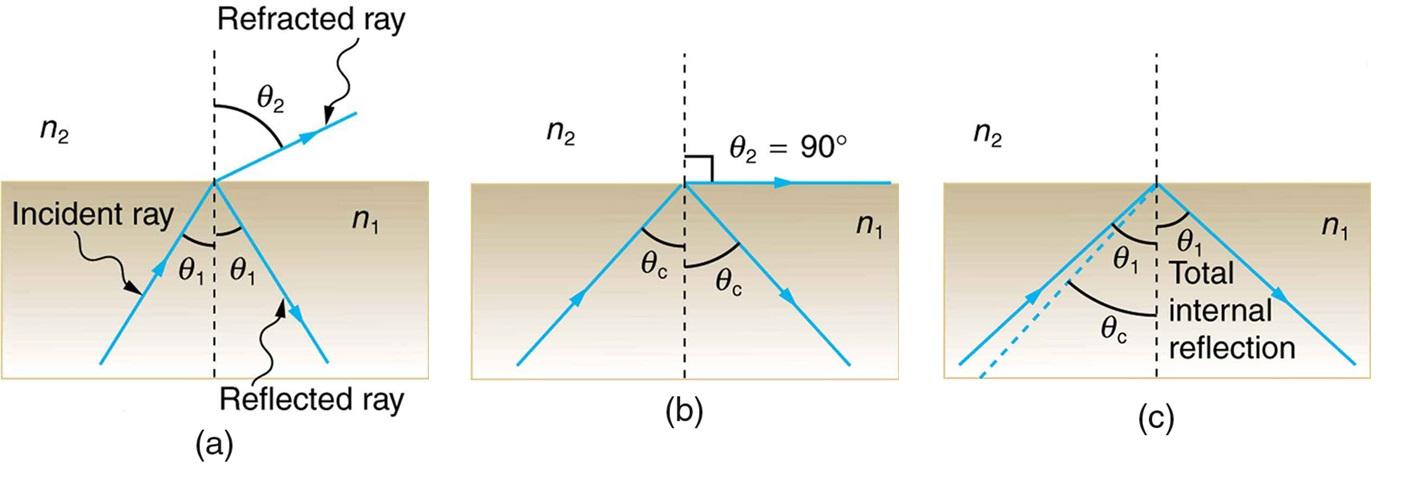
Considere o que acontece quando um raio de luz atinge a superfície entre dois materiais, como mostrado na Figura 1a. Parte da luz cruza o limite e é refratada; o resto é refletido. Se, conforme mostrado na figura, o índice de refração para o segundo meio for menor do que para o primeiro, o raio se afasta da perpendicular. (Uma vez que\(n_{1} \gt n_{2}\) o ângulo de refração é maior do que o ângulo de incidência — ou seja,\(\theta_{2} \gt \theta_{1}\).) Agora imagine o que acontece quando o ângulo de incidência aumenta. Isso também faz\(\theta_{2}\) com que aumente. O maior ângulo de refração\(\theta_{2}\) pode ser\(90^{\circ}\), conforme mostrado na Figura 1b. O ângulo crítico\(\theta_{c}\) para uma combinação de materiais é definido como sendo o ângulo de incidência\(\theta_{1}\) que produz um ângulo de refração de\(90^{\circ}\). Ou seja,\(\theta_{c}\) é o ângulo de incidência para o qual\(\theta_{2} = 90^{\circ}\). Se o ângulo de incidência\(\theta_{1}\) for maior que o ângulo crítico, conforme mostrado na Figura 1c, toda a luz será refletida de volta para o meio 1, uma condição chamada reflexão interna total.
ANGULO CRÍTICO
O ângulo de incidência\(\theta_{1}\) que produz um ângulo de refração de\(90^{\circ}\) é chamado de ângulo crítico,\(\theta_{c}\).
A lei de Snell estabelece a relação entre ângulos e índices de refração. É dado por
\[n_{1}\sin{\theta_{1}} = n_{2}\sin{\theta_{2}}\label{25.5.1}\]
Quando o ângulo de incidência é igual ao ângulo crítico (\(\theta_{1} = \theta_{c}\)), o ângulo de refração é\(90^{\circ}\) (\(\theta_{2} = 90^{\circ}\)). Observando que\(\sin{90^{\circ}} = 1\), a lei de Snell neste caso se torna
\[n_{1} \sin{\theta_{1}} = n_{2}\label{25.5.2}\]
O ângulo crítico\(\theta_{c}\) para uma determinada combinação de materiais é, portanto,
\[\theta_{c} = \sin{\left( n_{2} / n_{1} \right)}^{-1} \label{25.5.3}\]
para\(n_{1} \gt n_{2}\).
A reflexão interna total ocorre para qualquer ângulo incidente maior que o ângulo\(\theta_{c}\) crítico e só pode ocorrer quando o segundo meio tem um índice de refração menor que o primeiro. Observe que a equação acima foi escrita para um raio de luz que viaja no meio 1 e reflete a partir do meio 2, conforme mostrado na figura.
Exemplo\(\PageIndex{1}\): How Big is the Critical Angle Here?
Qual é o ângulo crítico para a luz que viaja em um tubo de poliestireno (um tipo de plástico) cercado por ar?
Estratégia:
O índice de refração do poliestireno é 1,49 e o índice de refração do ar pode ser considerado 1,00, como antes. Assim, a condição de que o segundo meio (ar) tenha um índice de refração menor que o primeiro (plástico) é satisfeita, e a equação\(\theta_{c} = \sin{\left( n_{2} / n_{1} \right)}^{-1}\) pode ser usada para encontrar o ângulo crítico\(\theta_{c}\) Aqui, então,\(n_{2} = 1.00\)\(n_{1} = 1.49\) e.
Solução
O ângulo crítico é dado por
\[\theta_{c} = \sin{\left( n_{2} / n_{1} \right)}^{-1} \nonumber.\]
Substituindo os valores identificados, obtém-se:
\[\begin{align*} \theta_{c} &= \sin{\left( 1.00 / 1.49 \right)}^{-1} \\[4pt] &= \sin{\left(0.671\right)}^{-1} \\[4pt] &= 42.2^{\circ}. \end{align*}\]
Discussão:
Isso significa que qualquer raio de luz dentro do plástico que atinja a superfície em um ângulo maior do que\(42.2^{\circ}\) será totalmente refletido. Isso fará da superfície interna do plástico transparente um espelho perfeito para esses raios, sem a necessidade do prateamento usado em espelhos comuns. Diferentes combinações de materiais têm ângulos críticos diferentes, mas qualquer combinação com\(n_{1} \gt n_{2}\) eles pode produzir reflexão interna total. O mesmo cálculo feito aqui mostra que o ângulo crítico para um raio que vai da água para o ar é\(48.6^{\circ}\), enquanto o do diamante para o ar é\(24.4^{\circ}\), e o do vidro de sílex para o vidro da coroa é\(66.3^{\circ}\). Não há reflexão total para os raios indo na outra direção — por exemplo, do ar para a água — já que a condição de que o segundo meio tenha um menor índice de refração não é satisfeita. Seguem-se várias aplicações interessantes da reflexão interna total.
Fibra óptica: endoscópios para telefones
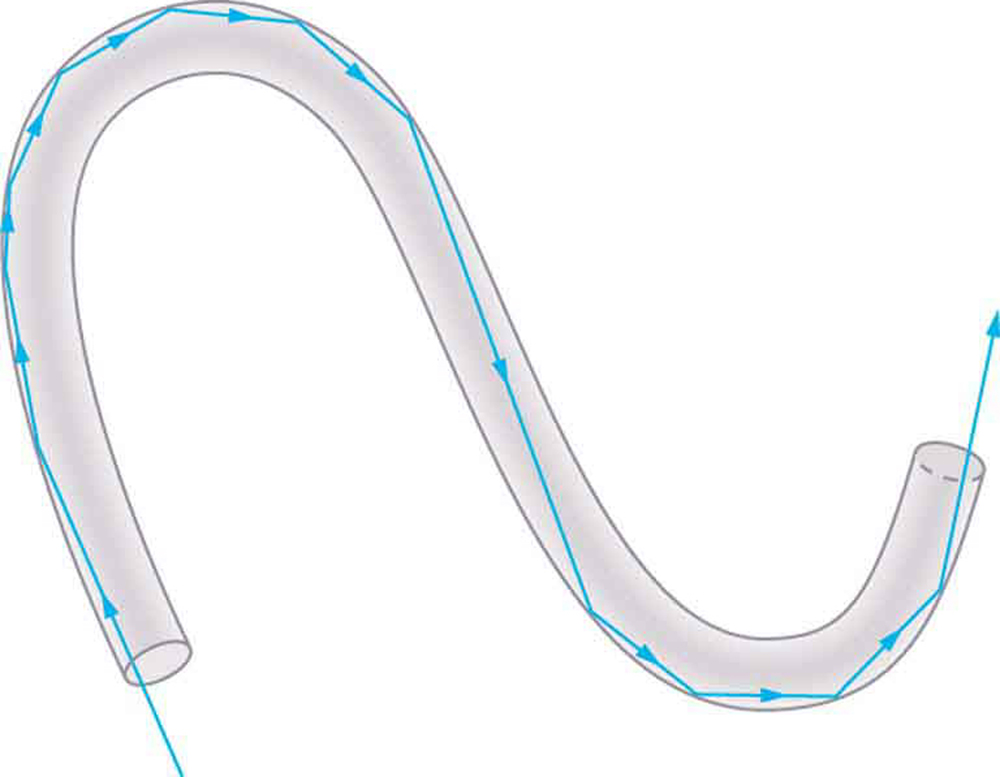
A fibra óptica é uma aplicação de reflexão interna total que é amplamente utilizada. Nas comunicações, é usado para transmitir sinais de telefone, internet e TV a cabo. A fibra óptica emprega a transmissão de fibras leves de plástico ou vidro. Como as fibras são finas, a luz que entra em uma delas provavelmente atingirá a superfície interna em um ângulo maior que o ângulo crítico e, portanto, será totalmente refletida (Figura\(\PageIndex{2}\)). O índice de refração externa da fibra deve ser menor do que o interno, uma condição que é facilmente satisfeita ao revestir a parte externa da fibra com um material com um índice de refração apropriado. Na verdade, a maioria das fibras tem um índice de refração variável para permitir que mais luz seja guiada ao longo da fibra por meio da refração interna total. Os raios são refletidos nos cantos, conforme mostrado, transformando as fibras em pequenos tubos de luz.
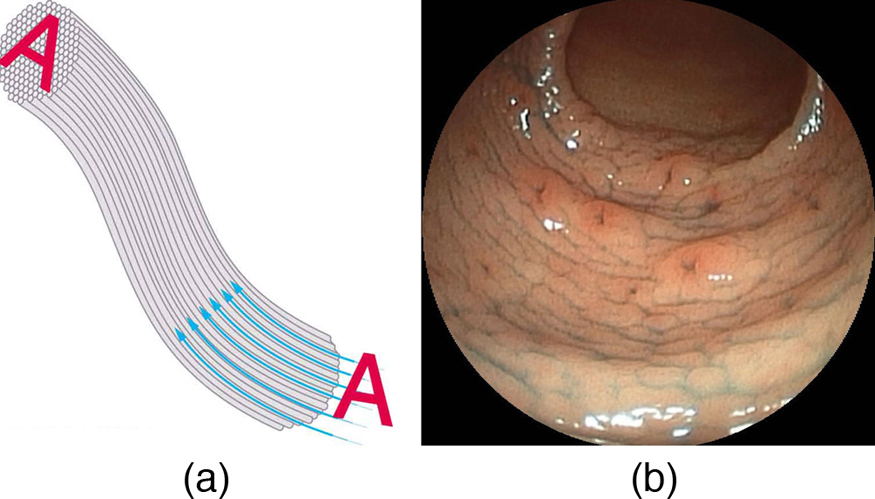
Feixes de fibras podem ser usados para transmitir uma imagem sem uma lente, conforme ilustrado na Figura\(\PageIndex{3}\). A saída de um dispositivo chamado endoscópio é mostrada na Figura\(\PageIndex{3b}\). Os endoscópios são usados para explorar o corpo através de vários orifícios ou pequenas incisões. A luz é transmitida por um feixe de fibras para iluminar as partes internas, e a luz refletida é transmitida de volta por outro para ser observada. A cirurgia pode ser realizada, como a cirurgia artroscópica na articulação do joelho, empregando ferramentas de corte acopladas e observadas com o endoscópio. As amostras também podem ser obtidas, por exemplo, laçando um pólipo intestinal para exame externo.
A fibra óptica revolucionou as técnicas cirúrgicas e as observações dentro do corpo. Há uma série de usos médicos, diagnósticos e terapêuticos. A flexibilidade do feixe de fibra óptica permite que ele navegue por regiões difíceis e pequenas do corpo, como intestinos, coração, vasos sanguíneos e articulações. A transmissão de um intenso feixe de laser para queimar placas obstrutivas nas principais artérias, bem como fornecer luz para ativar os medicamentos quimioterápicos, está se tornando comum. De fato, as fibras ópticas permitiram a microcirurgia e a cirurgia remota, onde as incisões são pequenas e os dedos do cirurgião não precisam tocar no tecido doente.
As fibras em feixes são cercadas por um material de revestimento que tem um índice de refração menor do que o núcleo (Figura\(\PageIndex{4}\)). O revestimento evita que a luz seja transmitida entre as fibras em um feixe. Sem revestimento, a luz pode passar entre as fibras em contato, pois seus índices de refração são idênticos. Como nenhuma luz entra no revestimento (há reflexão interna total de volta ao núcleo), nenhuma pode ser transmitida entre fibras revestidas que estão em contato umas com as outras. O revestimento evita que a luz escape da fibra; em vez disso, a maior parte da luz é propagada ao longo do comprimento da fibra, minimizando a perda de sinal e garantindo que uma imagem de qualidade seja formada na outra extremidade. O revestimento e uma camada protetora adicional tornam as fibras ópticas flexíveis e duráveis.
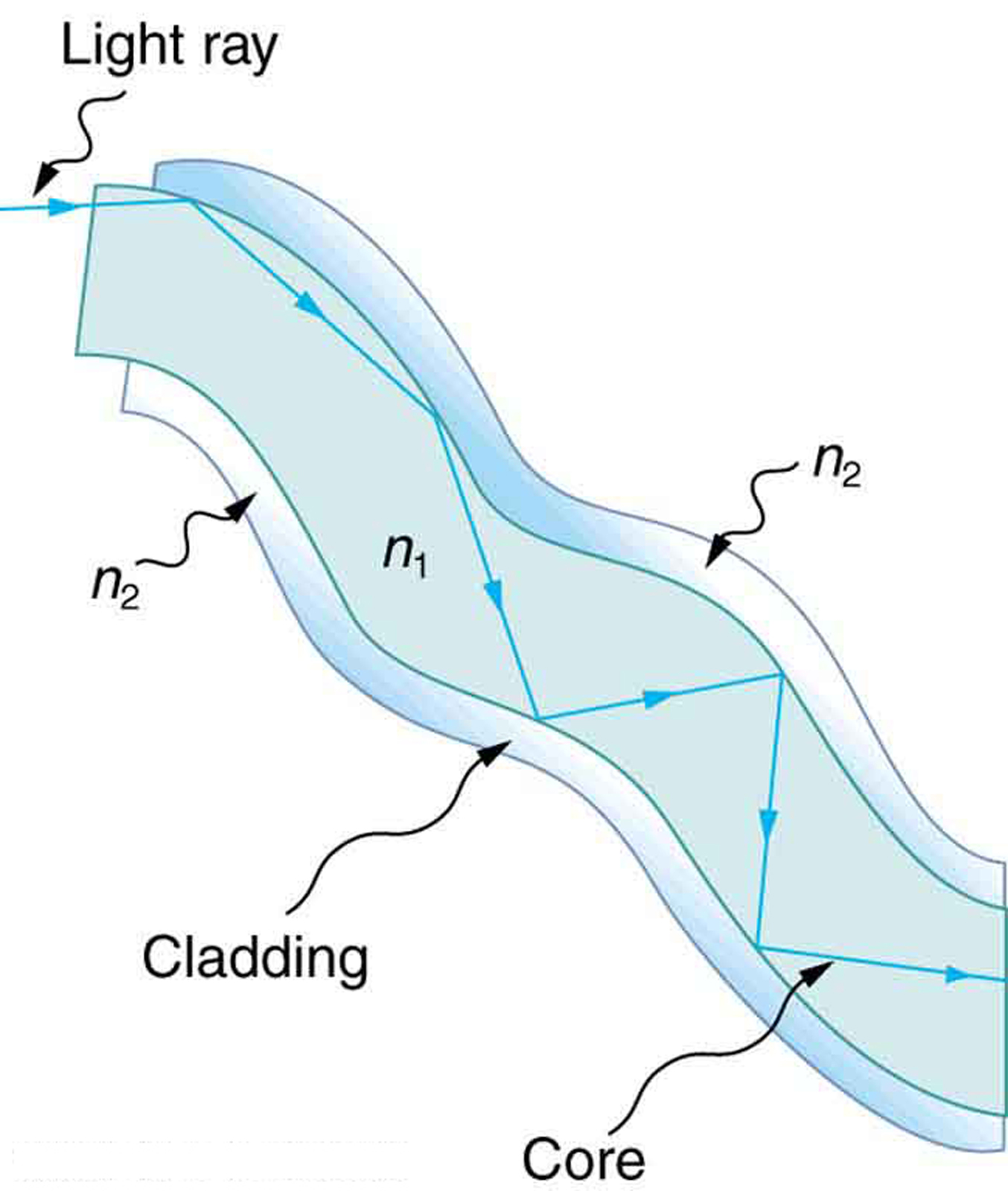
Revestimento
O revestimento evita que a luz seja transmitida entre as fibras em um feixe.
Lentes minúsculas especiais que podem ser fixadas nas extremidades dos feixes de fibras estão sendo projetadas e fabricadas. A luz emergindo de um feixe de fibras pode ser focalizada e uma pequena mancha pode ser fotografada. Em alguns casos, a mancha pode ser escaneada, permitindo imagens de qualidade de uma região dentro do corpo. Filtros ópticos especiais de minutos inseridos na extremidade do feixe de fibras têm a capacidade de obter imagens de dezenas de mícrons abaixo da superfície sem cortar a superfície — diagnósticos não intrusivos. Isso é particularmente útil para determinar a extensão dos cânceres no estômago e no intestino.
A maioria das conversas telefônicas e comunicações pela Internet agora são transmitidas por sinais de laser através de fibras ópticas. Cabos de fibra óptica extensos foram colocados no fundo do oceano e no subsolo para permitir comunicações ópticas. Os sistemas de comunicação por fibra óptica oferecem várias vantagens em relação aos sistemas elétricos (cobre), especialmente para longas distâncias. As fibras podem ser tão transparentes que a luz pode percorrer muitos quilômetros antes de ficar fraca o suficiente para exigir amplificação — muito superior aos condutores de cobre. Essa propriedade das fibras ópticas é chamada de baixa perda. Os lasers emitem luz com características que permitem muito mais conversas em uma fibra do que é possível com sinais elétricos em um único condutor. Essa propriedade das fibras ópticas é chamada de alta largura de banda. Sinais ópticos em uma fibra não produzem efeitos indesejáveis em outras fibras adjacentes. Essa propriedade das fibras ópticas é chamada de diafonia reduzida. Exploraremos as características únicas da radiação laser em um capítulo posterior.
Refletores de canto e diamantes
Um raio de luz que atinge um objeto que consiste em duas superfícies refletoras mutuamente perpendiculares é refletido de volta exatamente paralelamente à direção de onde veio. Isso é verdade sempre que as superfícies refletoras são perpendiculares e independentes do ângulo de incidência. Esse objeto, mostrado na Figura\(\PageIndex{5}\), é chamado de refletor de canto, pois a luz salta de seu canto interno. Muitos botões refletores baratos em bicicletas, carros e sinais de alerta têm refletores de canto projetados para retornar a luz na direção de onde ela se originou. Era mais caro para os astronautas colocarem um na lua. Os sinais de laser podem ser emitidos desse refletor de canto para medir a distância gradualmente crescente até a lua com grande precisão.

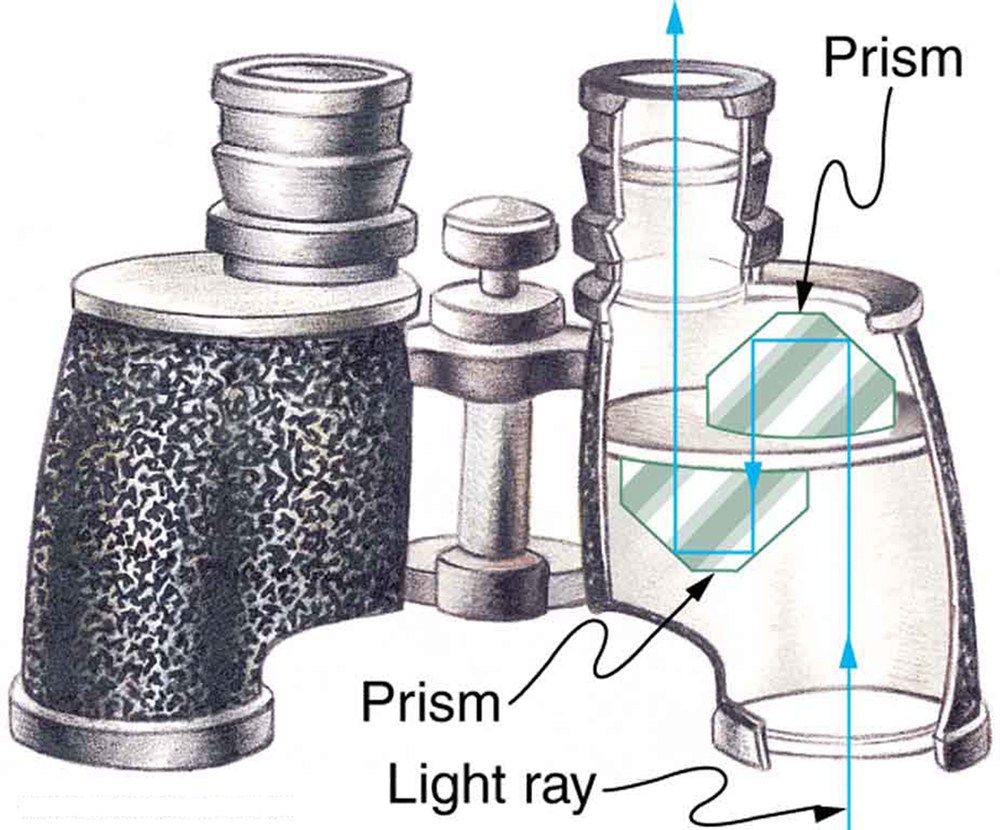
Os refletores de canto são perfeitamente eficientes quando as condições de reflexão interna total são satisfeitas. Com materiais comuns, é fácil obter um ângulo crítico menor que\(45^{\circ}\). Um uso desses espelhos perfeitos é em binóculos, conforme mostrado na Figura\(\PageIndex{6}\). Outro uso é em periscópios encontrados em submarinos.
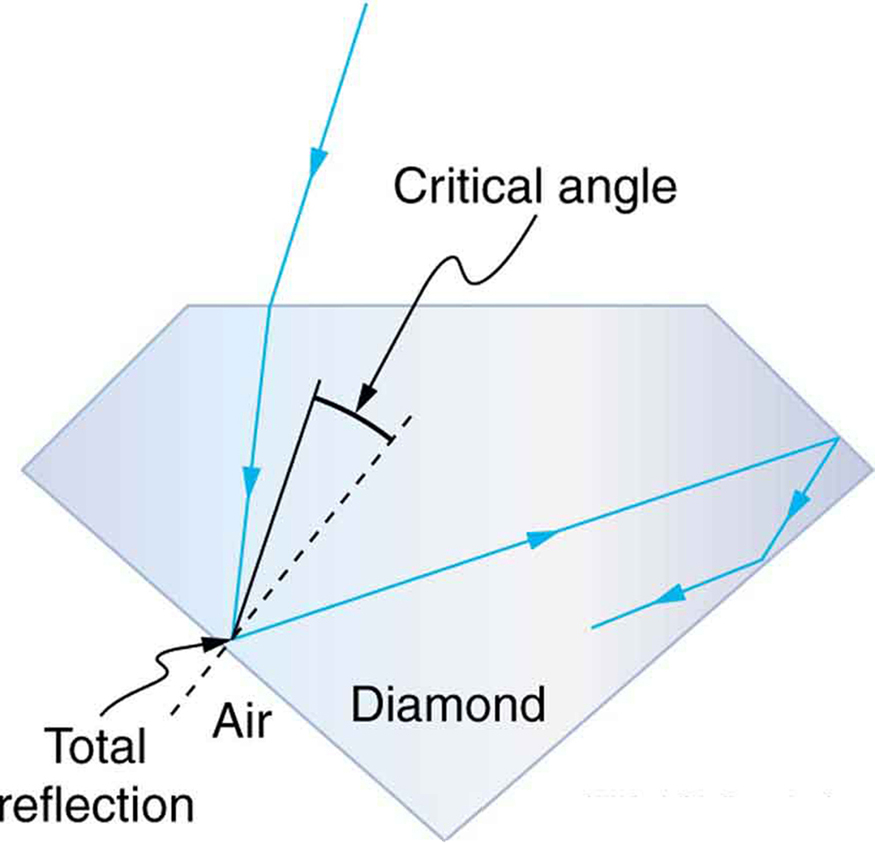
O brilho dos diamantes
A reflexão interna total, juntamente com um grande índice de refração, explica por que os diamantes brilham mais do que outros materiais. O ângulo crítico para uma superfície do diamante em relação ao ar é apenas e\(24.4^{\circ}\), portanto, quando a luz entra em um diamante, ela tem dificuldade em sair (Figura\(\PageIndex{7}\)). Embora a luz entre livremente no diamante, ela só pode sair se fizer um ângulo menor do que\(24.4^{\circ}\) as facetas dos diamantes são especificamente destinadas a tornar isso improvável, de modo que a luz possa sair apenas em certos lugares. Os bons diamantes são muito claros, de modo que a luz produz muitos reflexos internos e se concentra nos poucos lugares em que pode sair — daí o brilho. (O zircão é uma pedra preciosa natural que tem um índice de refração excepcionalmente grande, mas não tão grande quanto o diamante, por isso não é tão valorizada. A zircônia cúbica é fabricada e tem um índice de refração ainda maior (\(\sim 2.17\)), mas ainda menor que o do diamante.) As cores que você vê emergindo de um diamante cintilante não se devem à cor do diamante, que geralmente é quase incolor. Essas cores resultam da dispersão, o tópico “Dispersão: O arco-íris e os prismas” na próxima seção. Os diamantes coloridos obtêm sua cor devido a defeitos estruturais da estrutura cristalina e à inclusão de pequenas quantidades de grafite e outros materiais. A mina Argyle, na Austrália Ocidental, produz cerca de 90% dos diamantes rosa, vermelho, champanhe e conhaque do mundo, enquanto cerca de 50% dos diamantes transparentes do mundo vêm da África Central e Austral.
EXPLORAÇÕES DE PHET: LUZ CURVA
Explore a curvatura da luz entre dois meios com diferentes índices de refração. Veja como a mudança do ar para a água para o vidro altera o ângulo de curvatura. Brinque com prismas de diferentes formas e faça arco-íris.
Resumo
- O ângulo de incidência que produz um ângulo de refração de\(90^{\circ}\) é chamado de ângulo crítico.
- A reflexão interna total é um fenômeno que ocorre no limite entre dois meios, de forma que, se o ângulo de incidência no primeiro meio for maior que o ângulo crítico, toda a luz será refletida de volta para esse meio.
- A fibra óptica envolve a transmissão de luz por fibras de plástico ou vidro, aplicando o princípio da reflexão interna total.
- Os endoscópios são usados para explorar o corpo através de vários orifícios ou incisões menores, com base na transmissão de luz através de fibras ópticas.
- O revestimento evita que a luz seja transmitida entre as fibras em um feixe.
- Os diamantes brilham devido à reflexão interna total, juntamente com um grande índice de refração.
Glossário
- ângulo crítico
- ângulo de incidência que produz um ângulo de refração de\(90^{\circ}\)
- fibra óptica
- transmissão de luz por fibras de plástico ou vidro, aplicando o princípio da reflexão interna total
- refletor de canto
- um objeto que consiste em duas superfícies refletoras mutuamente perpendiculares, de modo que a luz que entra é refletida de volta exatamente paralelamente à direção de onde veio
- zircão
- pedra preciosa natural com um grande índice de refração


