Skip to main content
Global

25.3: A Lei da Refração

  1. Last updated
  2. Save as PDF
  • Page ID
    194939

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Determine o índice de refração, dada a velocidade da luz em um meio.

    É fácil notar algumas coisas estranhas ao olhar para um aquário. Por exemplo, você pode ver o mesmo peixe aparentando estar em dois lugares diferentes (Figura\(\PageIndex{1}\)). Isso ocorre porque a luz que vem do peixe para nós muda de direção quando sai do tanque e, nesse caso, ela pode percorrer dois caminhos diferentes para chegar aos nossos olhos. A mudança na direção de um raio de luz (vagamente chamada de curvatura) quando ele passa por variações na matéria é chamada de refração. A refração é responsável por uma grande variedade de fenômenos ópticos, desde a ação das lentes até a transmissão de voz por meio de fibras ópticas.

    Definição: REFRAÇÃO

    A mudança na direção de um raio de luz (vagamente chamada de curvatura) quando ele passa por variações na matéria é chamada de refração.

    VELOCIDADE DA LUZ

    A velocidade da luz\(c\) não afeta apenas a refração, é um dos conceitos centrais da teoria da relatividade de Einstein. À medida que a precisão das medições da velocidade da luz\(c\) foi melhorada, descobriu-se que não dependia da velocidade da fonte ou do observador. No entanto, a velocidade da luz varia de forma precisa com o material que ela atravessa. Esses fatos têm implicações de longo alcance, como veremos em “Relatividade Especial”. Ele faz conexões entre espaço e tempo e altera nossas expectativas de que todos os observadores meçam o mesmo tempo para o mesmo evento, por exemplo. A velocidade da luz é tão importante que seu valor no vácuo é uma das constantes mais fundamentais da natureza, além de ser uma das quatro unidades fundamentais do SI.

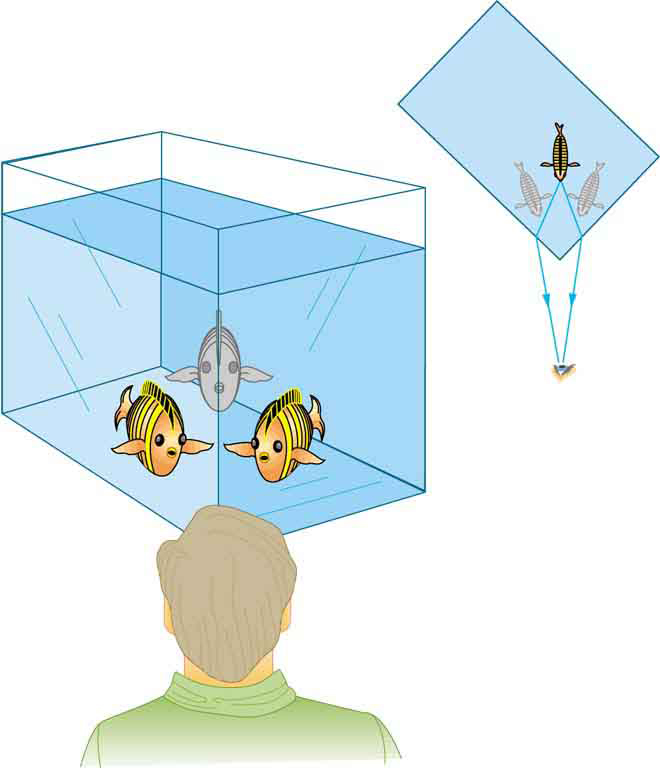
    Uma pessoa olha para um aquário e vê o mesmo peixe em duas direções diferentes na borda do tanque de água voltada para ele.
    Figura\(\PageIndex{1}\): Olhando para o aquário conforme mostrado, podemos ver o mesmo peixe em dois locais diferentes, porque a luz muda de direção quando passa da água para o ar. Nesse caso, a luz pode alcançar o observador por dois caminhos diferentes e, portanto, o peixe parece estar em dois lugares diferentes. Essa curvatura da luz é chamada de refração e é responsável por muitos fenômenos ópticos.

    Por que a luz muda de direção ao passar de um material (médio) para outro? É porque a luz muda de velocidade ao passar de um material para outro. Portanto, antes de estudarmos a lei da refração, é útil discutir a velocidade da luz e como ela varia em diferentes mídias.

    A velocidade da luz

    As primeiras tentativas de medir a velocidade da luz, como as feitas por Galileu, determinaram que a luz se movia extremamente rápido, talvez instantaneamente. A primeira evidência real de que a luz viajou a uma velocidade finita veio do astrônomo dinamarquês Ole Roemer no final do século XVII. Roemer observou que o período orbital médio de uma das luas de Júpiter, medido a partir da Terra, variava dependendo se a Terra estava se movendo em direção ou se afastando de Júpiter. Ele concluiu corretamente que a aparente mudança no período foi devido à mudança na distância entre a Terra e Júpiter e ao tempo que a luz levou para percorrer essa distância. A partir de seus dados de 1676, um valor da velocidade da luz foi calculado como sendo\(2.26 \times 10^{8} m/s\) (apenas 25% diferente do valor aceito atualmente). Em tempos mais recentes, os físicos mediram a velocidade da luz de várias maneiras e com precisão crescente. Um método particularmente direto, usado em 1887 pelo físico americano Albert Michelson (1852-1931), é ilustrado na Figura\(\PageIndex{2}\). A luz refletida por um conjunto rotativo de espelhos foi refletida de um espelho estacionário a 35 km de distância e retornou aos espelhos giratórios. O tempo de viagem da luz pode ser determinado pela rapidez com que os espelhos devem girar para que a luz retorne aos olhos do observador.

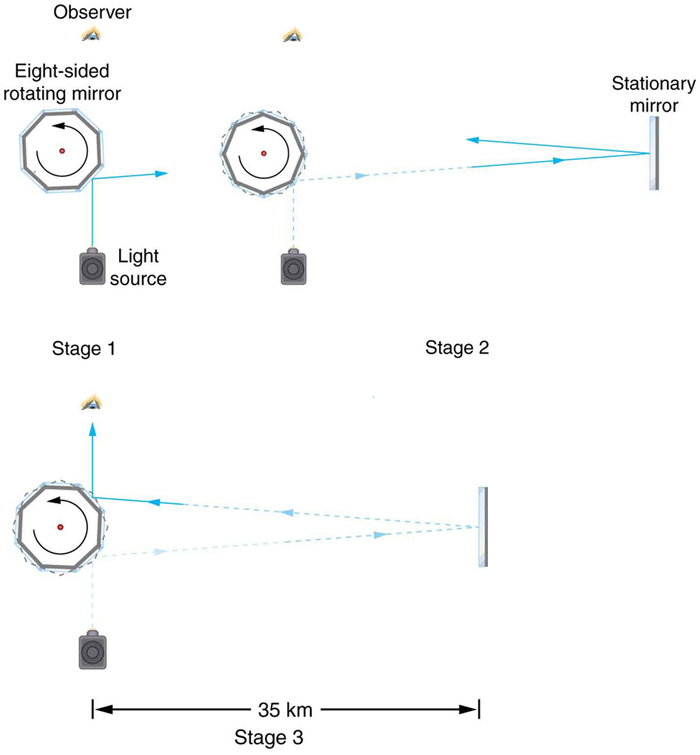
    No primeiro estágio da figura, a luz que cai de uma fonte em um espelho de oito lados é vista por um observador; no estágio dois, o espelho é feito para girar e a luz refletida que cai sobre um espelho estacionário mantido a uma certa distância de 35 quilômetros é vista por um observador. No estágio três, o observador pode ver o raio refletido somente quando o espelho gira na posição correta, assim como o raio retorna.
    Figura\(\PageIndex{2}\): Um esquema dos primeiros aparelhos usados por Michelson e outros para determinar a velocidade da luz. À medida que os espelhos giram, o raio refletido é direcionado apenas brevemente para o espelho estacionário. O raio de retorno será refletido no olho do observador somente se o próximo espelho tiver girado para a posição correta, assim como o raio retornar. Ao medir a taxa de rotação correta, o tempo da viagem de ida e volta pode ser medido e a velocidade da luz calculada. O valor calculado de Michelson da velocidade da luz foi apenas 0,04% diferente do valor usado hoje.

    A velocidade da luz agora é conhecida com grande precisão. De fato, a velocidade da luz no vácuo\(c\) é tão importante que é aceita como uma das quantidades físicas básicas e tem o valor fixo.

    VALOR DA VELOCIDADE DA LUZ

    \[\begin{align} c &\equiv 2.99792458 \times 10^{8} \\[5pt] &\sim 3.00 \times 10^{8} m/s \end{align}\]

    O valor aproximado de\(3.00 \times 10^{8} m/s\) é usado sempre que a precisão de três dígitos é suficiente. A velocidade da luz através da matéria é menor do que no vácuo, porque a luz interage com os átomos em um material. A velocidade da luz depende fortemente do tipo de material, pois sua interação com diferentes átomos, redes cristalinas e outras subestruturas varia.

    Definição: ÍNDICE DE REFRAÇÃO

    Definimos o índice de refração\(n\) de um material a ser

    \[n = \frac{c}{v}, \label{index}\]

    onde\(v\) está a velocidade da luz observada no material. Como a velocidade da luz é sempre menor do que\(c\) na matéria e é igual\(c\) somente no vácuo, o índice de refração é sempre maior ou igual a um. Isso é,\(n \gt 1\).

    A tabela\(\PageIndex{1}\) fornece os índices de refração de algumas substâncias representativas. Os valores são listados para um determinado comprimento de onda da luz, pois variam ligeiramente com o comprimento de onda. (Isso pode ter efeitos importantes, como cores produzidas por um prisma.) Observe que, para gases,\(n\) está próximo de 1,0. Isso parece razoável, já que os átomos nos gases são amplamente separados e a luz viaja\(c\) no vácuo entre os átomos. É comum usar gases, a\(n = 1\) menos que seja necessária uma grande precisão. Embora a velocidade da luz\( v\) em um meio varie consideravelmente de seu valor\( c\) no vácuo, ela ainda é uma velocidade grande.

    Tabela\(\PageIndex{1}\): Índice de refração em vários meios
    Médio n
    Gases em\(0ºC, 1 atm\)
    Ar 1.000 293
    Dióxido de carbono 1.00045
    Hidrogênio 1.000 139
    Oxigênio 1.000 271
    Líquidos a 20ºC
    Benzeno 1.501
    Dissulfeto de carbono 1.628
    Tetracloreto de carbono 1.461
    Etanol 1.361
    Glicerina 1.473
    Água fresca 1.333
    Sólidos a 20ºC
    Diamante 2.419
    Fluorita 1.434
    Vidro, coroa 1,52
    Vidro, sílex 1,66
    Gelo a 20ºC 1.309
    Poliestireno 1,49
    Acrílico 1,51
    Quartzo cristalino 1,544
    Quartzo, fundido 1.458
    Cloreto de sódio 1,544
    Zircão 1.923

    Exemplo\(\PageIndex{1}\): Speed of Light in Matter

    Calcule a velocidade da luz no zircão, um material usado em joias para imitar diamantes.

    Estratégia:

    A velocidade da luz em um material,\(v\), pode ser calculada a partir do índice de refração\(n\) do material usando a equação\(n = c/v\).

    Solução

    A equação para o índice de refração (Equation\ ref {index}) pode ser reorganizada para determinar\(v\)

    \[v = \frac{c}{n}. \nonumber\]

    O índice de refração do zircão é dado como 1,923 na Tabela\(\PageIndex{1}\) e\(c\) é dado na equação da velocidade da luz. A inserção desses valores na última expressão dá

    \[ \begin{align*} v &= \frac{3.00 \times 10^{8} m/s}{1.923} \\[5pt] &= 1.56 \times 10^{8} m/s. \end{align*}\]

    Discussão:

    Essa velocidade é um pouco maior que a metade da velocidade da luz no vácuo e ainda é alta em comparação com as velocidades que normalmente experimentamos. A única substância listada na Tabela\(\PageIndex{1}\) que tem um índice de refração maior do que o zircão é o diamante. Veremos mais tarde que o grande índice de refração do zircão faz com que ele brilhe mais do que o vidro, mas menos que o diamante.

    Lei da Refração

    A figura\(\PageIndex{3}\) mostra como um raio de luz muda de direção quando passa de um meio para outro. Como antes, os ângulos são medidos em relação a uma perpendicular à superfície no ponto em que o raio de luz a cruza. (Parte da luz incidente será refletida da superfície, mas por enquanto nos concentraremos na luz transmitida.) A mudança na direção do raio de luz depende de como a velocidade da luz muda. A mudança na velocidade da luz está relacionada aos índices de refração da mídia envolvida. Nas situações mostradas na Figura\(\PageIndex{3}\), o meio 2 tem um índice de refração maior do que o meio 1. Isso significa que a velocidade da luz é menor no meio 2 do que no meio 1. Observe que, conforme mostrado na Figura\(\PageIndex{3a}\), a direção do raio se aproxima da perpendicular quando diminui a velocidade. Por outro lado, conforme mostrado na Figura\(\PageIndex{3b}\), a direção do raio se afasta da perpendicular quando ele acelera. O caminho é exatamente reversível. Em ambos os casos, você pode imaginar o que acontece pensando em empurrar um cortador de grama de uma trilha para a grama e vice-versa. Indo da trilha para a grama, as rodas dianteiras são mais lentas e puxadas para o lado, conforme mostrado. Essa é a mesma mudança de direção da luz quando ela passa de um meio rápido para um lento. Ao ir da grama para a trilha, as rodas dianteiras podem se mover mais rápido e o cortador muda de direção conforme mostrado. Essa também é a mesma mudança de direção da luz que vai de lenta para rápida.

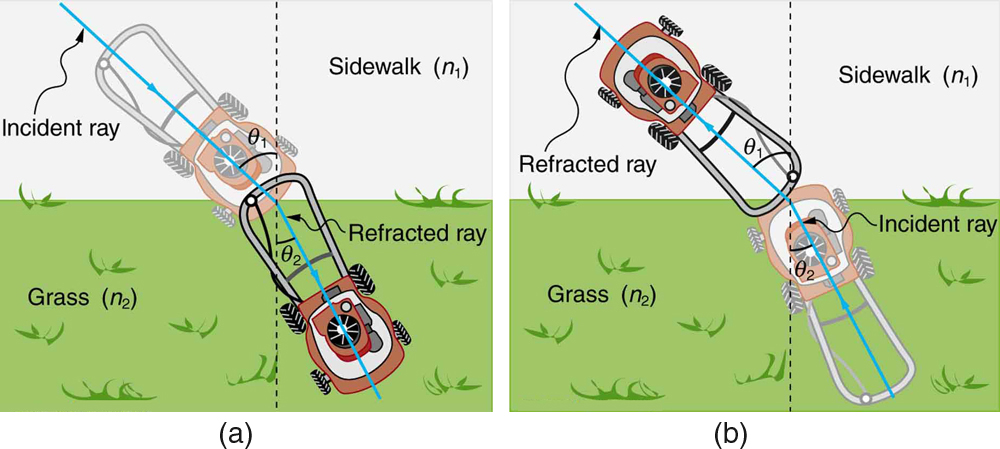
    Os números comparam o funcionamento de um cortador de grama ao do fenômeno de refração. Na figura (a), o cortador de grama vai da calçada à grama, desacelera e se curva em direção a uma perpendicular desenhada no ponto de contato do cortador com a superfície de separação. Uma linha imaginária ao longo do cortador quando ele está na calçada é considerado o raio incidente e o ângulo que o cortador faz com a perpendicular é considerado teta um. À medida que entra na grama, o cortador gira e a linha imaginária se move em direção à linha perpendicular desenhada e faz um ângulo teta dois com ele. A linha imaginária traçada ao longo do cortador quando o cortador está na grama é considerada o raio refratado. A calçada é considerada um meio de índice de refração n um e a da grama como n dois. Na figura (b), a situação é o inverso do que aconteceu na figura (a). O cortador se move da grama para a calçada e o raio de luz se afasta da perpendicular quando acelera.
    Figura\(\PageIndex{3}\): A mudança na direção de um raio de luz depende de como a velocidade da luz muda quando ele cruza de um meio para outro. A velocidade da luz é maior no meio 1 do que no meio 2 nas situações mostradas aqui. (a) Um raio de luz se aproxima da perpendicular quando diminui a velocidade. Isso é análogo ao que acontece quando um cortador de grama vai de uma trilha para a grama. (b) Um raio de luz se afasta da perpendicular quando acelera. Isso é análogo ao que acontece quando um cortador de grama vai da grama para a trilha. Os caminhos são exatamente reversíveis.

    A quantidade em que um raio de luz muda de direção depende tanto do ângulo de incidência quanto da mudança de velocidade. Para um raio em um determinado ângulo de incidência, uma grande mudança na velocidade causa uma grande mudança na direção e, portanto, uma grande mudança no ângulo. A relação matemática exata é a lei da refração, ou “Lei de Snell”, que é declarada em forma de equação como

    A LEI DA REFRAÇÃO (Lei de Snell)

    \[n_{1} \sin \theta_{1} = n_{2} \sin \theta_{2}.\label{25.4.2}\]

    Aqui,\(n_{1}\) e\(n_{2}\) estão os índices de refração para o meio 1 e 2,\(\theta_{1}\) e\(\theta_{2}\) são os ângulos entre os raios e a perpendicular no meio 1 e 2, conforme mostrado na Figura\(\PageIndex{3}\). O raio de entrada é chamado de raio incidente e o raio de saída de raio refratado, e os ângulos associados são o ângulo incidente e o ângulo refratado. A lei da refração também é chamada de lei de Snell em homenagem ao matemático holandês Willebrord Snell (1591-1626), que a descobriu em 1621. Os experimentos de Snell mostraram que a lei da refração foi obedecida e que um índice característico de refração\(n\) poderia ser atribuído a um determinado meio. Snell não sabia que a velocidade da luz variava em diferentes meios, mas por meio de experimentos ele foi capaz de determinar índices de refração a partir da forma como os raios de luz mudavam de direção.

    EXPERIÊNCIA PARA LEVAR PARA CASA: UM LÁPIS QUEBRADO

    Uma observação clássica da refração ocorre quando um lápis é colocado em um copo meio cheio de água. Faça isso e observe o formato do lápis ao olhar para o lápis de lado, ou seja, através do ar, do vidro, da água. Explique suas observações. Desenhe diagramas de raios para a situação.

    Exemplo\(\PageIndex{2}\): Determine the Index of Refraction from Refraction Data

    Encontre o índice de refração para o meio 2 na Figura\(\PageIndex{3a}\), assumindo que o meio 1 é ar e dado que o ângulo de incidência é\(30.0^{\circ}\) e o ângulo de refração é\(22.0^{\circ}\).

    Estratégia

    O índice de refração do ar é considerado 1 na maioria dos casos (e até quatro números significativos, é 1.000). Assim,\(n_{1} = 1.00\) aqui. A partir das informações fornecidas,\(\theta_{1} = 30.0^{\circ}\) e\(\theta_{2} = 22.0^{\circ}\) com essas informações, a única incógnita na lei de Snell é\(n_{2}\), para que ela possa ser usada para encontrar essa incógnita.

    Solução

    A lei de Snell (Equação\ ref {25.4.2}) pode ser reorganizada para isolar\(n_{2}\) dados

    \[n_{2} = n_{1}\frac{\sin{\theta_{1}}}{\sin{\theta_{2}}}.\]

    Inserindo valores conhecidos,

    \[ \begin{align*} n_{2} &= n_{1}\frac{\sin{30.0^{\circ}}}{\sin{22.0^{\circ}}} \\[5pt] &= \frac{0.500}{0.375} \\[5pt] &=1.33. \end{align*}\]

    Discussão

    Esse é o índice de refração da água, e Snell poderia tê-lo determinado medindo os ângulos e realizando esse cálculo. Ele então teria descoberto que 1,33 era o índice de refração apropriado para a água em todas as outras situações, como quando um raio passa da água para o vidro. Hoje, podemos verificar que o índice de refração está relacionado à velocidade da luz em um meio medindo essa velocidade diretamente.

    Exemplo\(\PageIndex{3}\): A Larger Change in Direction

    Suponha que em uma situação como a do exemplo anterior, a luz vá do ar para o diamante e que o ângulo de incidência seja\(30.0^{\circ}\). Calcule o ângulo de refração\(\theta_{2}\) no diamante.

    Estratégia

    Novamente, considera-se que o índice de refração do ar é\(n_{1} = 1.00\), e nós recebemos\(\theta_{1} = 30.0^{\circ}\). Podemos pesquisar o índice de refração do diamante na Tabela\(\PageIndex{1}\), encontrando\(n_{2} = 2.419\). A única incógnita na lei de Snell é\(\theta_{2}\) a que queremos determinar.

    Solução

    Resolvendo a lei de Snell (Equação\ ref {25.4.2}) para\(\sin{\theta_{2}}\) rendimentos

    \[ \sin{\theta_{2}} = \frac{n_{1}}{n_{2}}\sin{\theta_{1}}.\]

    Inserindo valores conhecidos,

    \[ \begin{align*} \sin{\theta_{2}} &= \frac{1.00}{2.419} \sin{30.0^{\circ}} \\[5pt] &= \left( 0.413 \right) \left( 0.500 \right) \\[5pt] &= 0.207. \end{align*}\]

    O ângulo é assim

    \[\theta_{2} = \sin{0.207}^{-1} = 11.9^{\circ}.\]

    Discussão

    Para o mesmo\(30^{\circ}\) ângulo de incidência, o ângulo de refração no diamante é significativamente menor do que na água (em\(11.9^{\circ}\) vez de\(22^{\circ}\) — veja o exemplo anterior).

    Resumo

    • A mudança na direção de um raio de luz quando ele passa por variações na matéria é chamada de refração.
    • A velocidade da luz no vácuo\(c = 2.99792458 \times 10^{8} \sim 3.00 \times 10^{8} m/s\)
    • O índice de refração\(n = \frac{c}{v}\), onde\(v\) é a velocidade da luz no material,\(c\) é a velocidade da luz no vácuo e\(n\) é o índice de refração.
    • A lei de Snell, a lei da refração, é declarada em forma de equação como\(n_{1} \sin_{\theta_{1}} = n_{2} \sin_{\theta_{2}}\).

    Glossário

    refração
    mudança da direção de um raio de luz quando ele passa por variações na matéria
    índice de refração
    para um material, a razão entre a velocidade da luz no vácuo e a do material