24.E: Ondas eletromagnéticas (exercícios)
- Page ID
- 195182
Perguntas conceituais
24.2: Produção de ondas eletromagnéticas
1. A direção do campo elétrico mostrada em cada parte da Figura 1 é aquela produzida pela distribuição de carga no fio. Justifique a direção mostrada em cada peça, usando a lei de força de Coulomb e a definição de\(\displaystyle E = F/q\), onde\(\displaystyle q\) está uma carga de teste positiva.
2. A direção do campo magnético mostrado na Figura 2a é consistente com a regra da direita para a corrente (RHR-2) na direção mostrada na figura?
3. Por que a direção da corrente mostrada em cada parte da Figura 2 é oposta ao campo elétrico produzido pela separação de carga do fio?
4. Em qual situação mostrada na figura a onda eletromagnética terá mais sucesso em induzir uma corrente no fio? Explique.
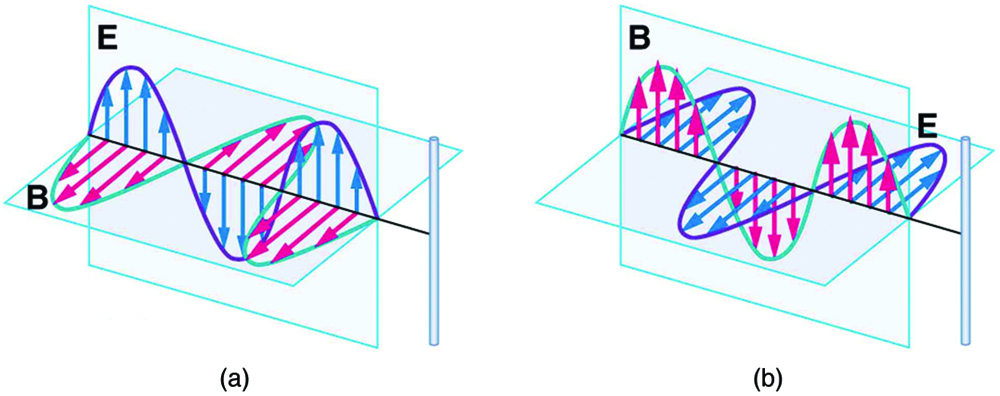
Ondas eletromagnéticas se aproximando de fios longos e retos.
5. Em qual situação mostrada na figura a onda eletromagnética terá mais sucesso em induzir uma corrente no circuito? Explique.
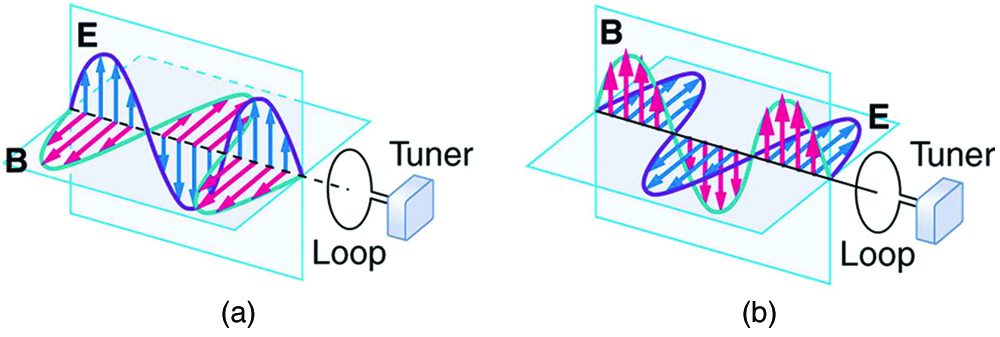
Ondas eletromagnéticas se aproximando de uma alça de arame.
6. A antena de fio reto de um rádio deve ser vertical ou horizontal para melhor receber as ondas de rádio transmitidas por uma antena transmissora vertical? Como uma antena circular deve ser alinhada para melhor receber os sinais? (Observe que a direção do loop que produz a melhor recepção pode ser usada para determinar a localização da fonte. É usado para esse propósito no rastreamento de animais marcados em estudos da natureza, por exemplo.)
7. Sob quais condições os fios de um circuito DC podem emitir ondas eletromagnéticas?
8. Dê um exemplo de interferência de ondas eletromagnéticas.
9. A figura mostra o padrão de interferência de duas antenas de rádio transmitindo o mesmo sinal. Explique como isso é análogo ao padrão de interferência do som produzido por dois alto-falantes. Isso poderia ser usado para criar um sistema de antena direcional que transmite preferencialmente em determinadas direções? Explique.
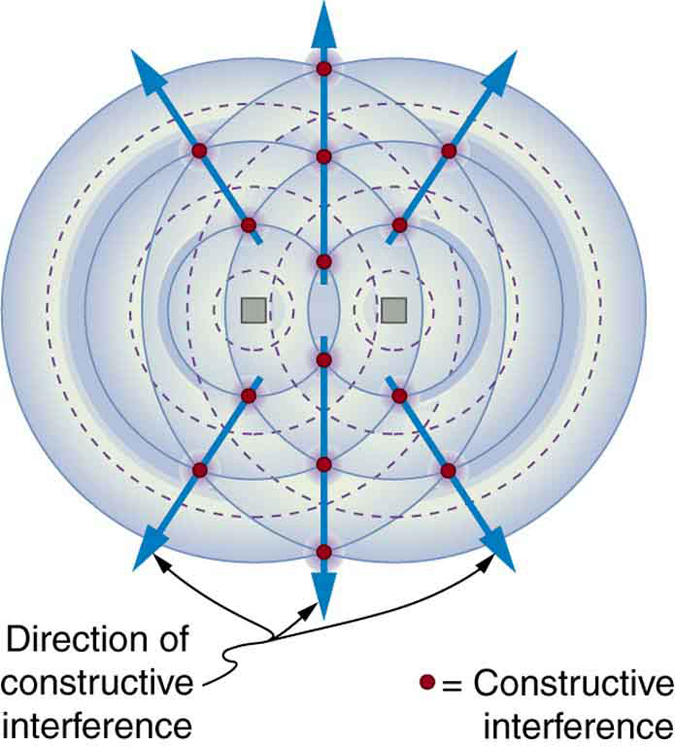
Uma visão aérea de duas antenas de transmissão de rádio que enviam o mesmo sinal e o padrão de interferência que elas produzem.
10. Uma antena pode ter qualquer comprimento? Explique sua resposta.
24.3: O espectro eletromagnético
11. Se você mora em uma região que tem uma estação de TV específica, às vezes você pode captar parte do áudio no receptor de rádio FM. Explique como isso é possível. Isso implica que o áudio da TV é transmitido como FM?
12. Explique por que as pessoas que têm a lente do olho removida por causa da catarata conseguem ver o ultravioleta de baixa frequência.
13. Como os resíduos de sabão fluorescente fazem com que as roupas pareçam “mais brilhantes e brancas” na luz externa? Isso seria eficaz à luz de velas?
14. Dê um exemplo de ressonância na recepção de ondas eletromagnéticas.
15. Ilustre que o tamanho dos detalhes de um objeto que pode ser detectado com ondas eletromagnéticas está relacionado ao seu comprimento de onda, comparando detalhes observáveis com dois tipos diferentes (por exemplo, radar e luz visível ou infravermelho e raios-X).
16. Por que os edifícios não bloqueiam as ondas de rádio tão completamente quanto a luz visível?
17. Faça uma lista de alguns objetos do cotidiano e decida se eles são transparentes ou opacos para cada um dos tipos de ondas eletromagnéticas.
18. Seu amigo diz que mais padrões e cores podem ser vistos nas asas dos pássaros se vistos sob luz ultravioleta. Você concordaria com seu amigo? Explique sua resposta.
19. A taxa na qual as informações podem ser transmitidas em uma onda eletromagnética é proporcional à frequência da onda. Isso é consistente com o fato de que a transmissão telefônica a laser em frequências visíveis carrega muito mais conversas por fibra óptica do que a transmissão eletrônica convencional em um fio? Qual é a implicação da comunicação por rádio da ELF com submarinos?
20. Dê um exemplo de energia transportada por uma onda eletromagnética.
21. Em uma ressonância magnética, um campo magnético mais alto requer ondas de rádio de maior frequência para ressoar com o tipo nuclear cuja densidade e localização estão sendo fotografadas. Qual o efeito de um campo magnético maior na antena mais eficiente para transmitir essas ondas de rádio? Isso favorece uma antena menor ou maior?
22. A correção da visão a laser geralmente usa um laser excimer que produz radiação eletromagnética de 193 nm. Esse comprimento de onda é extremamente fortemente absorvido pela córnea e o abla de uma maneira que remodela a córnea para corrigir defeitos de visão. Explique como a forte absorção ajuda a concentrar a energia em uma camada fina e, assim, dar maior precisão na modelagem da córnea. Explique também como essa forte absorção limita os danos ao cristalino e à retina do olho.
Problemas e exercícios
24.1: Equações de Maxwell: ondas eletromagnéticas previstas e observadas
23. Verifique se o valor correto para a velocidade da luz c é obtido quando valores numéricos para a permeabilidade e permissividade do espaço livre (\(\displaystyle mu_{0}\)e\(\displaystyle \epsilon_{0}\)) são inseridos no equação\(\displaystyle c = \frac{1}{\mu_{0}\epsilon_{0}}\).
24. Mostre que, quando as unidades SI para\(\displaystyle \mu_{0}\) e\(\displaystyle \epsilon_{0}\) são inseridas, as unidades dadas pelo lado direito da equação no problema acima são m/s.
24.2: Produção de ondas eletromagnéticas
25. Qual é a intensidade máxima do campo elétrico em uma onda eletromagnética que tem uma intensidade máxima de campo magnético de\(\displaystyle 5.00 \times 10^{-4} T\) (cerca de 10 vezes a da Terra)?
Solução
150 kV/m
26. A intensidade máxima do campo magnético de um campo eletromagnético é\(\displaystyle 5 \times 10^{-6} T\). Calcule a intensidade máxima do campo elétrico se a onda estiver viajando em um meio no qual a velocidade da onda esteja\(\displaystyle 0.75c\).
27. Verifique se as unidades obtidas para a intensidade\(\displaystyle B\) do campo magnético no exemplo do capítulo (usando a equação\(\displaystyle B = \frac{E}{c}\)) são na verdade teslas (T).
24.3: O espectro eletromagnético
28. (a) Duas frequências de microondas são autorizadas para uso em fornos de microondas: 900 e 2560 MHz. Calcule o comprimento de onda de cada um.
(b) Qual frequência produziria pontos quentes menores nos alimentos devido aos efeitos de interferência?
Solução
(a) 33,3 cm (900 MHz) 11,7 cm (2560 MHz)
(b) O forno de microondas com o menor comprimento de onda produziria pontos quentes menores nos alimentos, correspondendo àquele com a frequência de 2560 MHz.
29. (a) Calcule a faixa de comprimentos de onda para o rádio AM, dado que sua faixa de frequência é de 540 a 1600 kHz.
(b) Faça o mesmo para a faixa de frequência FM de 88,0 a 108 MHz.
30. Uma estação de rádio utiliza frequências entre AM e FM comerciais. Qual é a frequência de um canal de comprimento de onda de 11,12 m?
Solução
26,96 MHz
31. Encontre a faixa de frequência da luz visível, uma vez que ela abrange comprimentos de onda de 380 a 760 nm.
32. Pentear o cabelo leva ao excesso de elétrons no pente. Com que rapidez você teria que mover o pente para cima e para baixo para produzir luz vermelha?
Solução
\(\displaystyle 5.0 \times 10^{14}\) Hz
33. A radiação eletromagnética com comprimento de\(\displaystyle 15.0 - \mu m\) onda é classificada como radiação infravermelha. Qual é sua frequência?
34. Aproximadamente qual é o menor detalhe observável com um microscópio que usa luz ultravioleta de frequência\(\displaystyle 1.20 \times 10^{15} Hz\)?
Solução
\(\displaystyle \lambda = \frac{c}{f} = \frac{3.00 \times 10^{8} m/s}{1.20 \times 10^{15} Hz} = 2.50 \times 10^{-7} m\)
35. Um radar usado para detectar a presença de aeronaves recebe um pulso refletido em um objeto\(\displaystyle 6 \times 10^{-5} s\) após sua transmissão. Qual é a distância da estação de radar até o objeto refletivo?
36. Alguns sistemas de radar detectam o tamanho e a forma de objetos, como aeronaves e terrenos geológicos. Aproximadamente qual é o menor detalhe observável utilizando um radar de 500 MHz?
Solução
0,600 m
37. Determine o tempo necessário para que os raios X de frequência\(\displaystyle 3 \times 10^{18} Hz\) percorram (a) 1 mm e (b) 1 cm.
38. Se você deseja detectar detalhes do tamanho dos átomos (aproximadamente\(\displaystyle 1 \times 10^{-10} m\)) com radiação eletromagnética, ela deve ter um comprimento de onda aproximadamente desse tamanho.
(a) Qual é sua frequência?
(b) Que tipo de radiação eletromagnética pode ser essa?
Solução
(a)\(\displaystyle f = \frac{c}{\lambda} = \frac{3.00 \times 10^{8} m/s}{1 \times 10^{-10} m} = 3 \times 10^{18} Hz\)
(b) Raios-X
39. Se o Sol se desligasse repentinamente, não o saberíamos até que sua luz parasse de chegar. Quanto tempo isso duraria, considerando que o sol está\(\displaystyle 1.50 \times 10^{11} m\) ausente?
40. As distâncias no espaço são frequentemente citadas em unidades de anos-luz, a distância que a luz percorre em um ano.
(a) Quantos metros tem um ano-luz?
(b) Quantos metros estão até Andrômeda, a grande galáxia mais próxima, já que está a\(\displaystyle 2.00 \times 10^{6}\) anos-luz de distância?
(c) A galáxia mais distante já descoberta está a\(\displaystyle 12.0 \times 10^{9}\) anos-luz de distância. Qual é a distância em metros?
41. Uma certa linha de alimentação CA de 50,0 Hz irradia uma onda eletromagnética com uma intensidade máxima de campo elétrico de 13,0 kV/m.
(a) Qual é o comprimento de onda dessa onda eletromagnética de frequência muito baixa?
(b) Qual é a intensidade máxima do seu campo magnético?
Solução
(a)\(\displaystyle 6.00 \times 10^{6} m\)
(b)\(\displaystyle 4.33 \times 10^{-5} T\)
42. Durante o batimento normal, o coração cria um potencial máximo de 4,00 mV em 0,300 m do peito de uma pessoa, criando uma onda eletromagnética de 1,00 Hz.
(a) Qual é a intensidade máxima do campo elétrico criada?
(b) Qual é a intensidade máxima do campo magnético correspondente na onda eletromagnética?
(c) Qual é o comprimento de onda da onda eletromagnética?
43. (a) O tamanho ideal (mais eficiente) para uma antena de transmissão com uma extremidade no solo é um quarto do comprimento\(\displaystyle \lambda / 4 \) de onda (da radiação eletromagnética enviada). Se uma nova estação de rádio tiver uma antena com 50,0 m de altura, qual frequência ela transmite com mais eficiência? Isso é na banda AM ou FM?
(b) Discuta a analogia do modo ressonante fundamental de uma coluna de ar fechada em uma extremidade à ressonância de correntes em uma antena que tem um quarto de seu comprimento de onda.
Solução
(a)\(\displaystyle 1.50 \times 10^{6} Hz\), banda AM
(b) A ressonância das correntes em uma antena que é 1/4 de seu comprimento de onda é análoga ao modo ressonante fundamental de uma coluna de ar fechada em uma extremidade, já que o tubo também tem um comprimento igual a 1/4 do comprimento de onda do fundamental oscilação.
44. (a) Qual é o comprimento de onda das ondas de rádio de 100 MHz usadas em uma unidade de ressonância magnética?
(b) Se as frequências forem varridas em uma\(\displaystyle +/- 1.00\) faixa centrada em 100 MHz, qual é a faixa de comprimentos de onda transmitidos?
45. (a) Qual é a frequência da radiação ultravioleta de 193 nm usada na cirurgia ocular a laser?
(b) Supondo que a precisão com que essa radiação EM pode ablar a córnea seja diretamente proporcional ao comprimento de onda, quão mais preciso esse UV pode ser do que o menor comprimento de onda visível da luz?
Solução
(a)\(\displaystyle 1.55 \times 10^{15} Hz\)
(b) O menor comprimento de onda da luz visível é 380 nm, de modo que,\[\frac{\lambda_{visible}}{\lambda_{UV}}\]\[= \frac{380 nm}{193 nm}\]\[= 1.97.\] em outras palavras, a radiação UV é 97% mais precisa do que o menor comprimento de onda da luz visível, ou quase duas vezes mais precisa!
46. As antenas de recepção de TV para VHF são construídas com fios cruzados suportados em seus centros, conforme mostrado na Figura 15. O comprimento ideal para os fios cruzados é a metade do comprimento de onda a ser recebido, com as antenas mais caras tendo uma para cada canal. Suponha que você meça os comprimentos dos fios para canais específicos e descubra que eles têm 1,94 e 0,753 m de comprimento, respectivamente. Quais são as frequências desses canais?
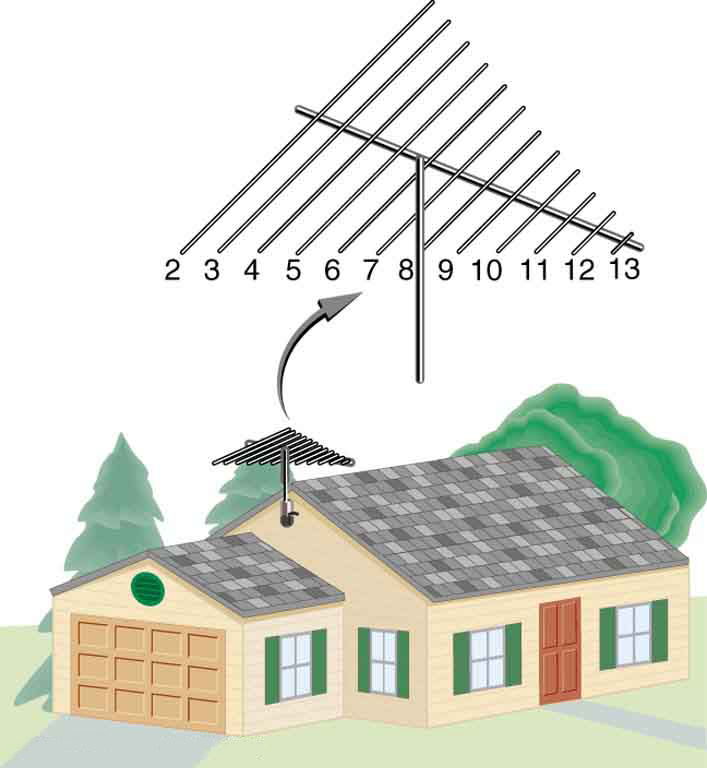
Uma antena de recepção de televisão tem fios cruzados de vários comprimentos para receber com mais eficiência diferentes comprimentos de onda.
47. As conversas com astronautas em caminhadas lunares tiveram um eco que foi usado para estimar a distância até a Lua. O som falado pela pessoa na Terra foi transformado em um sinal de rádio enviado à Lua e transformado novamente em som em um alto-falante dentro do traje espacial do astronauta. Esse som foi captado pelo microfone do traje espacial (destinado à voz do astronauta) e enviado de volta à Terra como uma espécie de eco de rádio. Se o tempo de ida e volta foi de 2,60 s, qual foi a distância aproximada até a Lua, negligenciando quaisquer atrasos na eletrônica?
Solução
\(\displaystyle 3.90 \times 10^{8} m\)
48. Os astronautas lunares colocaram um refletor na superfície da Lua, do qual um feixe de laser é refletido periodicamente. A distância até a Lua é calculada a partir do tempo de ida e volta.
(a) Com que precisão em metros a distância até a Lua pode ser determinada, se esse tempo puder ser medido até 0,100 ns?
(b) Qual porcentagem de precisão é essa, dada a distância média até a Lua\(\displaystyle 3.84 \times 10^{8} m\)?
49. O radar é usado para determinar distâncias até vários objetos medindo o tempo de ida e volta de um eco do objeto.
(a) A que distância está o planeta Vênus se o tempo de eco for de 1000 s?
(b) Qual é o tempo de eco de um carro a 75,0 m de uma unidade de radar da Polícia Rodoviária?
(c) Com que precisão (em nanossegundos) você deve ser capaz de medir o tempo de eco de um avião a 12,0 km de distância para determinar sua distância dentro de 10,0 m?
Solução
(a)\(\displaystyle 1.50 \times 10^{11} m\)
(b)\(\displaystyle 0.500 \mu s\)
(c) 66,7 ns
50. Conceitos integrados:
(a) Calcule a razão entre as frequências mais altas e mais baixas de ondas eletromagnéticas que o olho pode ver, dado que a faixa de comprimento de onda da luz visível é de 380 a 760 nm.
(b) Compare isso com a proporção das frequências mais altas e mais baixas que o ouvido pode ouvir.
51. Conceitos integrados:
(a) Calcule a taxa em watts na qual a transferência de calor através da radiação ocorre (quase inteiramente no infravermelho)\(\displaystyle 1.0 m^{2}\) da superfície da Terra à noite. Suponha que a emissividade seja 0,90, a temperatura da Terra seja\(\displaystyle 15^{\circ}C\) e a do espaço sideral seja 2,7 K.
(b) Compare a intensidade dessa radiação com a que vem do Sol para a Terra durante o dia, que tem uma média de cerca de\(\displaystyle 800 W/m^{2}\), apenas metade da qual é absorvida.
(c) Qual é a intensidade máxima do campo magnético na radiação de saída, supondo que seja uma onda contínua?
Solução
(a)\(\displaystyle -3.5 \times 10^{2} W/m^{2}\)
(b) 88%
(c)\(\displaystyle 1.7 \mu T\)
24.4: Energia em ondas eletromagnéticas
52. Qual é a intensidade de uma onda eletromagnética com um pico de intensidade de campo elétrico de 125 V/m?
Solução
\(\displaystyle I = \frac{c \epsilon_{0} E_{0}^{2}}{2}\)
\(\displaystyle = \frac{\left( 3.00 \times 10^{8} m/s \right) \left( 8.85 \times 10^{-12} C^{2} / N \cdot m^{2} \right) \left(125 V/m \right) ^{2}}{2}\)
\(\displaystyle = 20.7 W/m^{2}\)
53. Encontre a intensidade de uma onda eletromagnética com um pico de intensidade de campo magnético de\(\displaystyle 4.00 \times 10^{-9} T\).
54. Suponha que os lasers de hélio-néon comumente usados em laboratórios de física estudantil tenham saídas de potência de 0,250 mW.
(a) Se esse feixe de laser for projetado em um ponto circular de 1,00 mm de diâmetro, qual é sua intensidade?
(b) Encontre o pico de intensidade do campo magnético.
(c) Encontre a intensidade máxima do campo elétrico.
Solução
(a)\(\displaystyle I = \frac{P}{A} = \frac{P}{\pi r^{2}} = \frac{0.250 \times 10^{-3} W}{ \pi \left( 0.500 \times 10^{-3} m \right) ^{2}} = 318 W/m^{2}\)
\(\displaystyle I_{ave} = \frac{c B_{0}^{2}}{2 \mu_{0}} \rightarrow B_{0} = \left( \frac{2 \mu_{0}}{c}\right)^{1/2}\)
(b)\(\displaystyle = \left( \frac{2 \left(2 \pi \times 10^{-7} T \cdot m/A \right) \left( 318.3 W/m^{2} \right)}{ 3.00 \times 10^{8} m/s} \right) ^{1/2} \)
\(\displaystyle = 1.63 \times 10^{-6} T\)
(c)\(\displaystyle E_{0} = c B_{0} = \left( 3.00 \times 10^{8} m/s \right) \left(1.633 \times 10^{-6} T \right)\)
\(\displaystyle = 4.90 \times 10^{2} V/m\)
55. Um transmissor de rádio AM transmite 50,0 kW de potência uniformemente em todas as direções.
(a) Supondo que todas as ondas de rádio que atingem o solo sejam completamente absorvidas e que não haja absorção pela atmosfera ou por outros objetos, qual é a intensidade a 30,0 km de distância? (Dica: metade da energia será distribuída pela área de um hemisfério.)
(b) Qual é a intensidade máxima do campo elétrico a essa distância?
56. Suponha que a intensidade máxima segura das microondas para exposição humana seja considerada\(\displaystyle 1.00 W/m^{2}\).
(a) Se uma unidade de radar vazar 10,0 W de microondas (exceto aquelas enviadas por sua antena) uniformemente em todas as direções, a que distância você deve estar para ser exposto a uma intensidade considerada segura? Suponha que a energia se espalhe uniformemente sobre a área de uma esfera sem complicações de absorção ou reflexão.
(b) Qual é a intensidade máxima do campo elétrico na intensidade segura? (Observe que as primeiras unidades de radar vazaram mais do que as modernas. Isso causou problemas de saúde identificáveis, como catarata, para as pessoas que trabalhavam perto delas.)
Solução
(a) 89,2 cm
(b) 27,4 V/m
57. Uma antena parabólica de comunicações universitárias de 2,50 m de diâmetro recebe sinais de TV com uma intensidade máxima de campo elétrico (para um canal) de\(\displaystyle 7.50 \mu V/m\). (Veja a figura.) (a) Qual é a intensidade dessa onda? (b) Qual é a energia recebida pela antena? (c) Se o satélite em órbita transmitir uniformemente sobre uma área de\(\displaystyle 1.50 \times 10^{13} m^{2}\) (uma grande fração da América do Norte), quanta energia ele irradia?
As antenas parabólicas recebem sinais de TV enviados da órbita. Embora os sinais sejam bastante fracos, o receptor pode detectá-los sendo sintonizado para ressoar em sua frequência.
58. Lasers podem ser construídos para produzir uma onda eletromagnética de intensidade extremamente alta por um breve período — chamadas de lasers pulsados. Eles são usados para iniciar a fusão nuclear, por exemplo. Esse laser pode produzir uma onda eletromagnética com uma intensidade máxima de campo elétrico\(\displaystyle 1.00 \times 10^{11} V/m\) por um tempo de 1,00 ns.
(a) Qual é a intensidade máxima do campo magnético na onda?
(b) Qual é a intensidade do feixe?
(c) Que energia ela fornece em uma\(\displaystyle 1.00 - mm^{2}\) área?
Solução
(a) 33 T
(b)\(\displaystyle 1.33 \times 10^{19} W/m^{2}\)
(c) 13,3 kJ
59. Mostre que, para uma onda eletromagnética sinusoidal contínua, a intensidade máxima é o dobro da intensidade média (\(\displaystyle I_{0} = 2I_{ave}\)), usando o fato de que\(\displaystyle E_{0} = \sqrt{2}E_{rms}\), ou\(\displaystyle B_{0} = \sqrt{2}B_{rms}\), onde rms significa média (na verdade, raiz quadrada média, um tipo de média).
60. Suponha que uma fonte de ondas eletromagnéticas irradia uniformemente em todas as direções no espaço vazio onde não há efeitos de absorção ou interferência.
(a) Mostre que a intensidade é inversamente proporcional à\(\displaystyle r^{2}\) distância da fonte ao quadrado.
(b) Mostre que as magnitudes dos campos elétrico e magnético são inversamente proporcionais\(\displaystyle r\) a.
Solução
(a)\(\displaystyle I = \frac{P}{A} = \frac{P}{4 \pi r^{2}} \propto \frac{1}{r^{2}}\)
(b)\(\displaystyle I \propto E_{0}^{2}, B_{0}^{2} \rightarrow E_{0}^{2}, B_{0}^{2} \propto \frac{1}{r^{2}} \rightarrow E_{0}, B_{0} \propto \frac{1}{r}\)
61. Conceitos integrados
Um\(\displaystyle LC\) circuito com um capacitor de 5,00 pF oscila de forma a irradiar em um comprimento de onda de 3,30 m.
(a) Qual é a frequência de ressonância?
(b) Qual indutância está em série com o capacitor?
62. Conceitos integrados
Qual capacitância é necessária em série com um\(\displaystyle 800 - \mu H\) indutor para formar um circuito que irradia um comprimento de onda de 196 m?
Solução
13,5 pF
63. Conceitos integrados
O radar policial determina a velocidade dos veículos motorizados usando a mesma técnica Doppler-shift empregada para ultrassom em diagnósticos médicos. As batidas são produzidas misturando o eco duplo com desvio de Doppler com a frequência original. Se forem usadas\(\displaystyle 1.50 \times 10^{9} - Hz\) microondas e uma frequência de batida de 150 Hz for produzida, qual é a velocidade do veículo? (Suponha que as mesmas fórmulas de Doppler-shift sejam válidas com a velocidade do som substituída pela velocidade da luz.)
64. Conceitos integrados:
Suponha que a radiação principalmente infravermelha de uma lâmpada de calor aja como uma onda contínua com comprimento de onda\(\displaystyle 1.50 \mu m\).
(a) Se a saída de 200 W da lâmpada estiver focada no ombro de uma pessoa, em uma área circular de 25,0 cm de diâmetro, qual é a intensidade\(\displaystyle W/m^{12}\)?
(b) Qual é a intensidade máxima do campo elétrico?
(c) Encontre o pico de intensidade do campo magnético.
(d) Quanto tempo será necessário para aumentar a temperatura do ombro de 4,00 kg\(\displaystyle 2.00^{\circ}C\), assumindo que não há outra transferência de calor e considerando que seu calor específico é\(\displaystyle 3.47 \times 10^{3} J/kg \cdot ^{\circ}C\)?
Solução
(a)\(\displaystyle 4.07 kW/m^{2}\)
(b) 1,75 kV/m
(c)\(\displaystyle 5.84 \mu T\)
(d) 2 min 19 s
65. Conceitos integrados:
Em sua configuração de maior potência, um forno de microondas aumenta a temperatura de 0,400 kg de espaguete\(\displaystyle 45.0^{\circ}C\) em 120 s.
(a) Qual foi a taxa de absorção de energia pelo espaguete, considerando que seu calor específico é\(\displaystyle 3.76 \times 10^{3} J/kg \cdot ^{\circ}C\)?
(b) Determine a intensidade média das microondas, uma vez que elas são absorvidas em uma área circular de 20,0 cm de diâmetro.
(c) Qual é a intensidade máxima do campo elétrico do micro-ondas? (d) Qual é o seu pico de intensidade de campo magnético?
66. Conceitos integrados:
A radiação eletromagnética de um laser de 5,00 mW está concentrada em uma\(\displaystyle 1.00 - mm^{2}\) área.
(a) Qual é a intensidade em\(\displaystyle W/ m^{2}\)?
(b) Suponha que uma carga estática de 2,00-nC esteja no feixe. Qual é a força elétrica máxima que ele experimenta?
(c) Se a carga estática se mover a 400 m/s, qual força magnética máxima ela pode sentir?
Solução
(a)\(\displaystyle 5.00 \times 10^{3} W/m^{2}\)
(b)\(\displaystyle 3.88 \times 10^{-6} N\)
(c)\(\displaystyle 5.18 \times 10^{-12} N\)
67. Conceitos integrados:
Uma bobina plana de 200 voltas de fio de 30,0 cm de diâmetro atua como uma antena para rádio FM a uma frequência de 100 MHz. O campo magnético da onda eletromagnética de entrada é perpendicular à bobina e tem uma força máxima de\(\displaystyle 1.00 \times 10^{-12} T\).
(a) Qual energia incide sobre a bobina?
(b) Qual emf médio é induzido na bobina durante um quarto de um ciclo?
(c) Se o receptor de rádio tiver uma indutância de\(\displaystyle 2.50 \mu H\), qual capacitância ele deve ter para ressoar a 100 MHz?
68. Conceitos integrados:
Se as intensidades do campo elétrico e magnético variarem sinusoidalmente no tempo, sendo zero em\(\displaystyle t = 0\), então\(\displaystyle E = E_{0} \sin{2 \pi} ft\)\(\displaystyle B = B_{0} \sin{2 \pi} ft\) e. Deixe\(\displaystyle f = 1.00 GHz\) aqui.
(a) Quando as forças de campo são zeradas pela primeira vez?
(b) Quando eles atingem seu valor mais negativo?
(c) Quanto tempo é necessário para que eles concluam um ciclo?
Solução
(a)\(\displaystyle t = 0\)
(b)\(\displaystyle 7.50 \times 10^{-10} s\)
(c)\(\displaystyle 1.00 \times 10^{-9} s\)
69. Resultados irracionais:
Um pesquisador mede o comprimento de onda de uma onda eletromagnética de 1,20 GHz em 0,500 m.
(a) Calcule a velocidade com que essa onda se propaga.
(b) O que não é razoável nesse resultado?
(c) Quais suposições são irracionais ou inconsistentes?
70. Resultados irracionais:
O pico de intensidade do campo magnético em um forno de microondas residencial é\(\displaystyle 9.20 \times 10^{-5} T\).
(a) Qual é a intensidade do micro-ondas?
(b) O que não é razoável nesse resultado?
(c) O que há de errado na premissa?
Solução
(a)\(\displaystyle 1.01 \times 10^{6} W/m^{2}\)
(b) Muito boa para um forno.
(c) O campo magnético assumido é excessivamente grande.
71. Resultados irracionais:
Um\(\displaystyle LC\) circuito contendo um indutor de 2,00-H oscila a uma frequência tal que irradia em um comprimento de onda de 1,00 m.
(a) Qual é a capacitância do circuito?
(b) O que não é razoável nesse resultado?
(c) Quais suposições são irracionais ou inconsistentes?
72. Resultados irracionais:
Um\(\displaystyle LC\) circuito contendo um capacitor de 1,00 pF oscila em tal frequência que irradia em um comprimento de onda de 300 nm.
(a) Qual é a indutância do circuito?
(b) O que não é razoável nesse resultado?
(c) Quais suposições são irracionais ou inconsistentes?
A solução
(a)\(\displaystyle 2.53 \times 10^{-20} H\)
(b) L é muito pequena.
(c) O comprimento de onda é excessivamente pequeno.
73. Crie seu próprio problema:
Considere os campos eletromagnéticos produzidos por linhas elétricas de alta tensão. Crie um problema no qual você calcule a intensidade dessa radiação eletromagnética\(\displaystyle W/m^{2}\) com base na intensidade medida do campo magnético da radiação em uma casa próxima às linhas de energia. Suponha que essas intensidades do campo magnético sejam conhecidas por terem uma média inferior a\(\displaystyle \mu T\) a. A intensidade é pequena o suficiente para que seja difícil imaginar mecanismos de danos biológicos causados por ela. Discuta a quantidade de energia que pode estar irradiando de uma seção da linha de energia com várias centenas de metros de comprimento e compare isso com a potência que provavelmente será transportada pelas linhas. Uma ideia de quanta potência isso é pode ser obtida calculando a corrente aproximada responsável pelos\(\displaystyle \mu T\) campos a distâncias de dezenas de metros.
74. Crie seu próprio problema:
Considere a geração mais recente de antenas parabólicas residenciais com pouco menos de meio metro de diâmetro. Crie um problema no qual você calcule a potência recebida pela antena e a intensidade máxima do campo elétrico dos sinais de microondas para um único canal recebido pela antena. Entre as coisas a serem consideradas estão a energia transmitida pelo satélite e a área pela qual a energia é distribuída, bem como a área da antena receptora.


