Skip to main content
Global

24.4: Energia em ondas eletromagnéticas

  1. Last updated
  2. Save as PDF
  • Page ID
    195180

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    objetivos de aprendizagem

    Ao final desta seção, você poderá:

    • Explique como a energia e a amplitude de uma onda eletromagnética estão relacionadas.
    • Dada sua potência e a área de aquecimento, calcule a intensidade do campo eletromagnético de um forno de microondas, bem como suas intensidades de pico de campo elétrico e magnético

    Qualquer pessoa que tenha usado um forno de microondas sabe que há energia nas ondas eletromagnéticas. Às vezes, essa energia é óbvia, como no calor do sol de verão. Outras vezes, é sutil, como a energia não sentida dos raios gama, que pode destruir as células vivas.

    As ondas eletromagnéticas podem trazer energia para um sistema em virtude de seus campos elétricos e magnéticos. Esses campos podem exercer forças e mover cargas no sistema e, assim, trabalhar neles. Se a frequência da onda eletromagnética for a mesma das frequências naturais do sistema (como microondas na frequência de ressonância das moléculas de água), a transferência de energia é muito mais eficiente.

    CONEXÕES: ONDAS E PARTÍCULAS

    O comportamento da radiação eletromagnética exibe claramente as características das ondas. Mas descobriremos em módulos posteriores que, em altas frequências, a radiação eletromagnética também exibe características de partículas. Essas características das partículas serão usadas para explicar mais sobre as propriedades do espectro eletromagnético e para introduzir o estudo formal da física moderna.

    Outra descoberta surpreendente da física moderna é que partículas, como elétrons e prótons, exibem características de onda. Esse compartilhamento simultâneo de propriedades de ondas e partículas para todas as entidades submicroscópicas é uma das grandes simetrias da natureza.

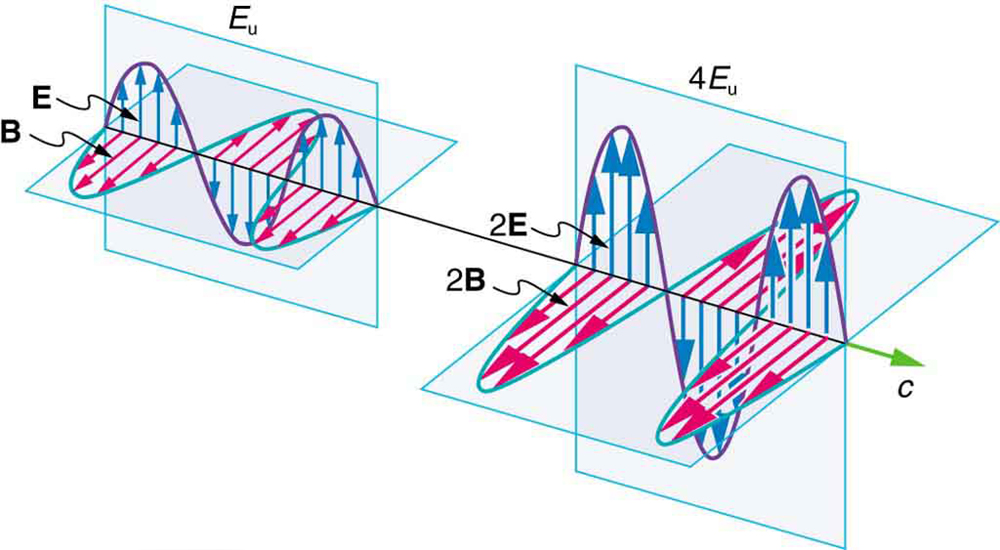
    A propagação de duas ondas eletromagnéticas é mostrada em planos tridimensionais. A primeira onda mostra com a variação de dois componentes E e B. E é uma onda senoidal em um plano com pequenas setas mostrando as vibrações das partículas no plano. B é uma onda senoidal em um plano perpendicular à onda E. A onda B tem setas para mostrar as vibrações das partículas no plano. As ondas são mostradas se cruzando na junção dos planos porque E e B são perpendiculares entre si. A direção de propagação da onda é mostrada perpendicularmente às ondas E e B. A energia transportada é dada como E sub u. A segunda onda mostra com a variação dos componentes duas E e duas ondas B, ou seja, ondas E e B com o dobro da amplitude do primeiro caso. Dois E é uma onda senoidal em um plano com pequenas setas mostrando as vibrações das partículas no plano. Dois B é uma onda senoidal em um plano perpendicular às duas ondas E. As duas ondas B têm setas para mostrar as vibrações das partículas no plano. As ondas são mostradas se cruzando na junção dos planos porque duas ondas E e duas ondas B são perpendiculares uma à outra. A direção de propagação da onda é mostrada perpendicularmente a duas ondas E e duas ondas B. A energia transportada é dada como quatro E sub u.
    Figura\(\PageIndex{1}\): A energia transportada por uma onda é proporcional ao quadrado de sua amplitude. Com ondas eletromagnéticas,\(E\) campos e\(B\) campos maiores exercem forças maiores e podem fazer mais trabalho.

    Mas há energia em uma onda eletromagnética, seja ela absorvida ou não. Uma vez criados, os campos transportam energia para longe de uma fonte. Se absorvidas, as forças do campo diminuem e tudo o que sobra viaja. Claramente, quanto maior a intensidade dos campos elétrico e magnético, mais trabalho eles podem fazer e maior a energia que a onda eletromagnética carrega.

    A energia de uma onda é proporcional à sua amplitude ao quadrado (\(E^{2}\)ou\(B^{2}\)). Isso vale para ondas em cordas de guitarra, ondas de água e ondas sonoras, onde a amplitude é proporcional à pressão. Nas ondas eletromagnéticas, a amplitude é a intensidade máxima de campo dos campos elétrico e magnético. (Veja a Figura 1.)

    Assim, a energia transportada e a intensidade\(I\) de uma onda eletromagnética são proporcionais a\(E^{2}\)\(B^{2}\) e. De fato, para uma onda eletromagnética sinusoidal contínua, a intensidade média\[I_{ave} = \frac{c \epsilon_{0} E_{0}^{2}}{2},\label{24.5.1}\] onde\(c\) é a velocidade da luz,\(\epsilon_{0}\) é a permissividade do espaço livre e\(E_{0}\) é a intensidade máxima do campo elétrico; a intensidade, como sempre, é a potência por unidade de área (aqui em\(W/m^{2}\)).

    A intensidade média de uma onda eletromagnética também\(I_{ave}\) pode ser expressa em termos da intensidade do campo magnético usando a relação\(B = E/c\) e o fato de que\(\epsilon_{0} = 1/ \mu_{0} c^{2}\), onde\(\mu_{0}\) está a permeabilidade do espaço livre. A manipulação algébrica produz a relação\[I_{ave} = \frac{cB_{0}^{2}}{2 \mu_{0}}, \label{24.5.2}\] onde\(B_{0}\) está a intensidade máxima do campo magnético.

    Mais uma expressão para\(I_{ave}\) em termos de intensidade de campo elétrico e magnético é útil. Substituindo o fato de que\(c \cdot B_{0} = E_{0}\), as expressões anteriores se tornam\[I_{ave} = \frac{E_{0} B_{0}}{2 \mu_{0}} . \label{24.5.3}\] Qualquer uma das três equações anteriores mais conveniente pode ser usada, pois na verdade são apenas versões diferentes do mesmo princípio: a energia em uma onda está relacionada à amplitude quadrada. Além disso, como essas equações são baseadas na suposição de que as ondas eletromagnéticas são senoidais, a intensidade máxima é o dobro da média; ou seja,\(I_{0} = 2I_{ave}\).

    Exemplo\(\PageIndex{1}\): Calculate Microwave Intensities and Fields

    Em sua configuração de potência mais alta, um determinado forno de microondas projeta 1,00 kW de microondas em uma área de 30,0 por 40,0 cm. (a) Qual é a intensidade em\(W/m^{2}\)? (b) Calcule a intensidade máxima do campo elétrico\(E_{0}\) nessas ondas. (c) Qual é a intensidade máxima do campo magnético\(B_{0}\)?

    Estratégia:

    Na parte (a), podemos encontrar intensidade a partir de sua definição como potência por unidade de área. Uma vez conhecida a intensidade, podemos usar as equações abaixo para encontrar as intensidades de campo solicitadas nas partes (b) e (c).

    Solução para (a):

    Inserindo a potência dada na definição de intensidade, e observando que a área é de 0,300 por 0,400 m, produz\[I = \frac{P}{A} = \frac{1.00 kW}{0.300 m \times 0.400 m}.\] Aqui\(I = I_{ave}\), de modo que\[I_{ave} = \frac{1000 W}{0.120 m^{2}} = 8.33 \times 10^{3} W/m^{2}.\] Observe que a intensidade máxima é o dobro da média:\[I_{0} = 2I_{ave} = 1.67 \times 10^{4} W/m^{2}.\]

    Solução para (b):

    Para descobrir\(E_{0}\), podemos reorganizar a primeira equação dada acima para\(I_{ave}\) dar\[E_{0} = \left( \frac{2I_{ave}}{c \epsilon_{0}} \right) ^{1/2} .\] Inserindo valores conhecidos dá\[E_{0} = \sqrt{\frac{ 2 \left( 8.33 \times 10^{3} W/m^{2} \right) }{ \left( 3.00 \times 10^{8} m/s \right) \left( 8.85 \times 10^{-12} C^{2} / N \cdot m^{2} \right) }}\]\[= 2.51 \times 10^{3} V/m.\]

    Solução para (c):

    Talvez a maneira mais fácil de encontrar a intensidade do campo magnético, agora que a intensidade do campo elétrico é conhecida, seja usar a relação dada pela\[B_{0} = \frac{E_{0}}{c}.\] inserção de valores conhecidos dá\[B_{0} = \frac{2.51 \times 10^{3} V/m}{3.0 \times 10^{8} m/s}\]\[= 8.35 \times 10^{-6} T\]

    Discussão:

    Como antes, um campo elétrico relativamente forte é acompanhado por um campo magnético relativamente fraco em uma onda eletromagnética, pois\(B = E/c\), e\(c\) é um número grande.

    Resumo

    • A energia transportada por qualquer onda é proporcional ao quadrado de sua amplitude. Para ondas eletromagnéticas, isso significa que a intensidade pode ser expressa como\[I_{ave} = \frac{c \epsilon_{0} E_{0}^{2}}{2},\] onde\(I_{ave}\) está a intensidade média em\(W/m^{2}\) e\(E_{0}\) é a intensidade máxima do campo elétrico de uma onda senoidal contínua.
    • Isso também pode ser expresso em termos da intensidade\(B_{0}\) máxima do campo magnético\[I_{ave} = \frac{c B_{0}^{2}}{2 \mu_{0}}\] e em termos de campos elétricos e magnéticos como\[I_{ave} = \frac{E_{0}B_{0}}{2 \mu_{0}}.\]
    • As três expressões para\(I_{ave}\) são todas equivalentes.

    Glossário

    intensidade máxima de campo
    a amplitude máxima que uma onda eletromagnética pode atingir, representando a quantidade máxima de força elétrica e/ou fluxo magnético que a onda pode exercer
    intensidade
    a potência de um campo elétrico ou magnético por unidade de área, por exemplo, Watts por metro quadrado