23.10: Transformadores
- Page ID
- 194980
Objetivos de
Ao final desta seção, você poderá:
- Explique como um transformador funciona.
- Calcule a tensão, a corrente e/ou o número de voltas dadas as outras quantidades.
Os transformadores fazem o que seu nome indica: eles transformam tensões de um valor para outro (o termo tensão é usado em vez de emf, porque os transformadores têm resistência interna). Por exemplo, muitos telefones celulares, laptops, videogames, ferramentas elétricas e pequenos aparelhos têm um transformador embutido em sua unidade de encaixe (como na Figura\(\PageIndex{1}\)) que transforma 120 V ou 240 V CA em qualquer voltagem usada pelo dispositivo.

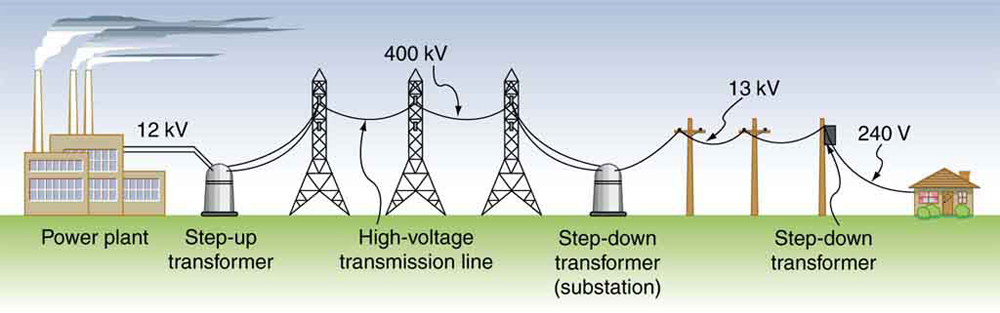
Os transformadores também são usados em vários pontos dos sistemas de distribuição de energia, como ilustrado na Figura\(\PageIndex{2}\). A energia é enviada a longas distâncias em altas tensões, porque menos corrente é necessária para uma determinada quantidade de energia, e isso significa menos perda de linha, conforme discutido anteriormente. Mas altas tensões representam maiores riscos, de modo que transformadores são empregados para produzir voltagem mais baixa no local do usuário.
O tipo de transformador considerado neste texto (Figura\(\PageIndex{3}\)) é baseado na lei de indução de Faraday e é muito semelhante em construção ao aparelho usado por Faraday para demonstrar que campos magnéticos poderiam causar correntes. As duas bobinas são chamadas de bobinas primárias e secundárias. Em uso normal, a tensão de entrada é colocada no primário e o secundário produz a tensão de saída transformada. O núcleo de ferro não apenas retém o campo magnético criado pela bobina primária, mas sua magnetização aumenta a intensidade do campo. Como a tensão de entrada é CA, um fluxo magnético variável no tempo é enviado para o secundário, induzindo sua tensão de saída CA.
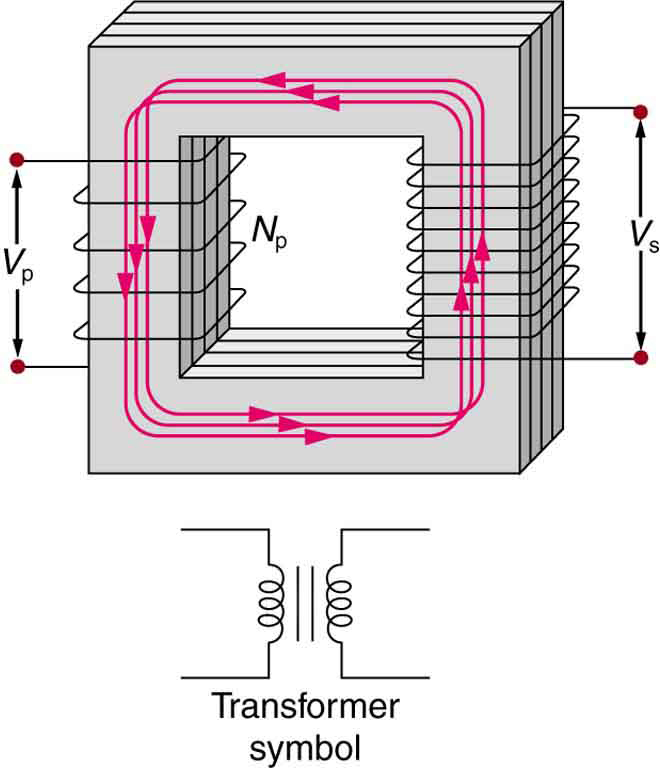
Para o transformador simples mostrado na Figura\(\PageIndex{3}\), a tensão de saída\(V_{s}\) depende quase inteiramente da tensão de entrada\(V_{p}\) e da relação entre o número de loops nas bobinas primária e secundária. A lei de indução de Faraday para a bobina secundária determina que sua tensão\(V_{s}\) de saída induzida seja
\[V_{s} = -N\dfrac{\Delta \Phi}{\Delta t},\label{23.8.1}\]
onde\(N_{s}\) está o número de loops na bobina secundária e\(\Delta \Phi / \Delta t\) é a taxa de variação do fluxo magnético. Observe que a tensão de saída é igual à emf induzida (\(V_{s} = emf_{s}\)), desde que a resistência da bobina seja pequena (uma suposição razoável para transformadores). A área da seção transversal das bobinas é a mesma em ambos os lados, assim como a intensidade do campo magnético, assim como\(\Delta \Phi / \Delta t\) a mesma em ambos os lados. A tensão primária de entrada também\(V_{p}\) está relacionada à mudança de fluxo por
\[V_{p} = -N_{p}\dfrac{\Delta \Phi}{\Delta t}.\label{23.8.2}\]
A razão para isso é um pouco mais sutil. A lei de Lenz nos diz que a bobina primária se opõe à mudança no fluxo causada pela tensão de entrada\(V_{p}\), daí o sinal de menos (este é um exemplo de autoindutância, um tópico a ser explorado com alguns detalhes nas seções posteriores). Assumindo uma resistência insignificante da bobina, a regra de circuito de Kirchhoff nos diz que o emf induzido é exatamente igual à tensão de entrada. Tomar a proporção dessas duas últimas equações produz uma relação útil:
\[\dfrac{V_{s}}{V_{p}} = \dfrac{N_{s}}{N_{p}}.\label{23.8.3}\]
Isso é conhecido como equação do transformador e simplesmente afirma que a razão entre as tensões secundárias e primárias em um transformador é igual à razão do número de voltas em suas bobinas.
A tensão de saída de um transformador pode ser menor, maior ou igual à tensão de entrada, dependendo da proporção do número de loops em suas bobinas. Alguns transformadores até fornecem uma saída variável, permitindo que a conexão seja feita em diferentes pontos da bobina secundária. Um transformador elevador é aquele que aumenta a tensão, enquanto um transformador redutor diminui a tensão. Supondo, como temos, que a resistência seja insignificante, a saída de energia elétrica de um transformador é igual à sua entrada. Isso é quase verdade na prática — a eficiência do transformador geralmente excede 99%. Equacionando a entrada e a saída de energia,
\[P_{p} = I_{p}V_{p} = I_{s}V_{s} = P_{s}.\label{23.8.4}\]
A reorganização dos termos dá
\[\dfrac{V_{s}}{V_{p}} = \dfrac{I_{p}}{I_{s}}.\label{23.8.6}\]
Combinando isso com a Equação\ ref {23.8.3}, descobrimos que
\[\dfrac{I_{s}}{I_{p}} = \dfrac{N_{p}}{N_{s}}.\label{23.8.7}\]
é a relação entre as correntes de saída e entrada de um transformador. Portanto, se a tensão aumentar, a corrente diminui. Por outro lado, se a tensão diminuir, a corrente aumenta.
Exemplo\(\PageIndex{1}\): Calculating Characteristics of a Step-Up Transformer
Uma unidade de raio-x portátil tem um transformador intensificador, cuja entrada de 120 V é transformada na saída de 100 kV necessária para o tubo de raio-x. O primário tem 50 loops e consome uma corrente de 10,00 A quando em uso. (a) Qual é o número de loops no secundário? (b) Encontre a saída atual do secundário.
Estratégia e solução para (a):
Resolvemos a Equação\ ref {23.8.3} para\(N_{s}\), o número de loops no secundário e inserimos os valores conhecidos. Isso dá
\[\begin{align*} N_{s} &= N_{p}\dfrac{V_{s}}{V_{p}} \\[5pt] &= \left(50\right) \dfrac{100,000 V}{120 V} \\[5pt] &= 4.17 \times 10^{4}. \end{align*}\]
Discussão para (a):
É necessário um grande número de loops no secundário (em comparação com o primário) para produzir uma tensão tão grande. Isso seria verdade para transformadores de sinais de néon e aqueles que fornecem alta tensão dentro de TVs e CRTs.
Estratégia e solução para (b):
Da mesma forma, podemos encontrar a corrente de saída do secundário resolvendo a Equação\ ref {23.8.7}\(I_{s}\) e inserindo valores conhecidos. Isso dá
\[\begin{align*} I_{s} &= I_{p}\dfrac{N_{p}}{N_{s}} \\[5pt] &= \left(10.00 A \right) \dfrac{50}{4.17 \times 10^{4}} \\[5pt] &= 12.0 mA. \end{align*}\]
Discussão para (b):
Como esperado, a saída atual é significativamente menor que a entrada. Em certas demonstrações espetaculares, voltagens muito grandes são usadas para produzir arcos longos, mas são relativamente seguras porque a saída do transformador não fornece uma grande corrente. Observe que a entrada de energia aqui é
\[\begin{align*}P_{p} = I_{p}V_{p} &= \left(10.00 A \right) \left(120 V \right) \\[5pt] &= 1.20 kW. \end{align*}\]
Isso é igual à saída de energia
\[\begin{align*} P_{p} = I_{s}V_{s} &= \left(12.0 mA \right) \left(100kV \right) \\[5pt] &= 1.20 kW \end{align*}\]
como assumimos na derivação das equações usadas.
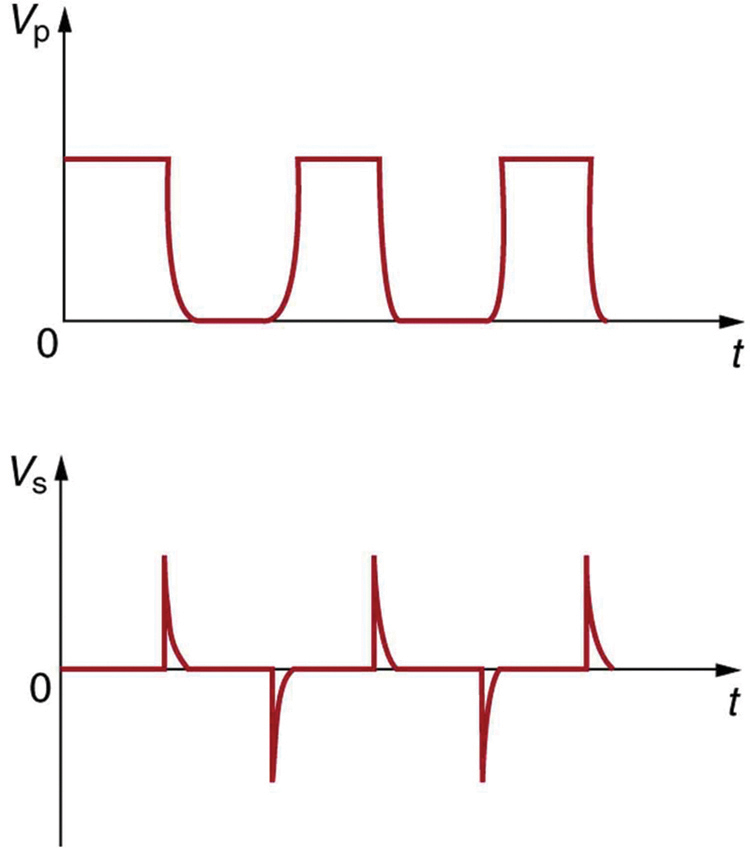
O fato de os transformadores serem baseados na lei de indução de Faraday deixa claro por que não podemos usar transformadores para alterar as tensões DC. Se não houver alteração na tensão primária, não haverá tensão induzida na secundária. Uma possibilidade é conectar o DC à bobina primária por meio de um interruptor. Quando o interruptor é aberto e fechado, o secundário produz uma voltagem como a da Figura\(\PageIndex{4}\). Essa não é realmente uma alternativa prática, e a corrente alternada é de uso comum sempre que necessário aumentar ou diminuir as tensões.
Exemplo\(\PageIndex{2}\): Calculating Characteristics of a Step-Down Transformer
Um carregador de bateria destinado a uma conexão em série de dez baterias de níquel-cádmio (emf total de 12,5 V DC) precisa ter uma saída de 15,0 V para carregar as baterias. Ele usa um transformador redutor com um primário de 200 circuitos e uma entrada de 120 V. (a) Quantos loops devem existir na bobina secundária? (b) Se a corrente de carga for 16,0 A, qual é a corrente de entrada?
Estratégia e solução para (a):
Você esperaria que o secundário tivesse um pequeno número de loops. Resolvendo a equação\ ref {23.8.3} para\(N_{s}\) e inserindo valores conhecidos fornece
\[\begin{align*} N_{s} &= N_{p}\dfrac{V_{s}}{V_{p}} \\[5pt] &= \left( 200 \right) \dfrac{15.0 V}{120 V} \\[5pt] &= 25. \end{align*}\]
Estratégia e solução para (b):
A entrada atual pode ser obtida resolvendo a Equação\ ref {23.8.7} para\(I_{p}\) e inserindo valores conhecidos. Isso dá
\[\begin{align*} I_{p} = I_{s}\dfrac{N_{s}}{N_{p}} \\[5pt] &= \left( 16.0 A \right) \dfrac{25}{200} \\[5pt] &= 2.00 A. \end{align*}\]
Discussão:
O número de loops no secundário é pequeno, conforme esperado para um transformador redutor. Também vemos que uma pequena corrente de entrada produz uma corrente de saída maior em um transformador redutor. Quando os transformadores são usados para operar ímãs grandes, às vezes eles têm um pequeno número de loops muito pesados no secundário. Isso permite que o secundário tenha baixa resistência interna e produza grandes correntes. Observe novamente que essa solução se baseia na suposição de 100% de eficiência — ou a saída de energia é igual à entrada de energia (\(P_{p} = P_{s}\)) — razoável para bons transformadores. Nesse caso, a potência primária e secundária é de 240 W. (verifique isso por si mesmo como uma verificação de consistência). Observe que as baterias Ni-Cd precisam ser carregadas de uma fonte de alimentação DC (assim como uma bateria de 12 V). Portanto, a saída CA da bobina secundária precisa ser convertida em DC. Isso é feito usando algo chamado retificador, que usa dispositivos chamados diodos que permitem apenas um fluxo unidirecional de corrente.
Os transformadores têm muitas aplicações em sistemas de segurança elétrica, que são discutidas em 23.9.
EXPLORAÇÕES PHET: GERADOR
Gere eletricidade com uma barra magnética! Descubra a física por trás dos fenômenos explorando ímãs e como você pode usá-los para fazer uma lâmpada acender.

Resumo
- Os transformadores usam indução para transformar tensões de um valor para outro.
- Para um transformador, as tensões nas bobinas primária e secundária estão relacionadas por\[\dfrac{V_{s}}{V_{p}} = \dfrac{N_{s}}{N_{p}},\] onde\(V_{p}\) e\(V_{s}\) as tensões nas bobinas primárias e secundárias têm\(N_{p}\) e\(N_{s}\) voltas.
- As correntes\(I_{p}\) e\(I_{s}\) nas bobinas primária e secundária estão relacionadas por\(\dfrac{I_{s}}{I_{p}} = \dfrac{N_{p}}{N_{s}}.\)
- Um transformador elevatório aumenta a tensão e diminui a corrente, enquanto um transformador redutor diminui a tensão e aumenta a corrente.
Glossário
- transformador
- um dispositivo que transforma tensões de um valor para outro usando indução
- equação do transformador
- a equação que mostra que a razão entre as tensões secundárias e primárias em um transformador é igual à razão do número de voltas em suas bobinas;\(\dfrac{V_{s}}{V_{p}} = \dfrac{N_{s}}{N_{p}}\)
- transformador step-up
- um transformador que aumenta a tensão
- transformador redutor
- um transformador que diminui a tensão


