23.8: Geradores elétricos

Last updated
Save as PDF

Page ID: 195114

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Calcule o emf induzido em um gerador.
Calcule o pico de emf que pode ser induzido em um sistema gerador específico.

Geradores elétricos induzem um emf girando uma bobina em um campo magnético, conforme discutido brevemente em “Emf induzido e fluxo magnético”. Agora vamos explorar os geradores com mais detalhes. Considere o exemplo a seguir.

Exemplo\(\PageIndex{1}\): Calculating the Emf Induced in a Generator Coil

A bobina do gerador mostrada na Figura\(\PageIndex{1}\) é girada em um quarto de uma revolução (de\(\theta = 0^{\circ}\) para\(\theta = 90^{\circ}\)) em 15,0 ms. A bobina circular de 200 voltas tem um raio de 5,00 cm e está em um campo magnético uniforme de 1,25 T. Qual é a média de emf induzida?

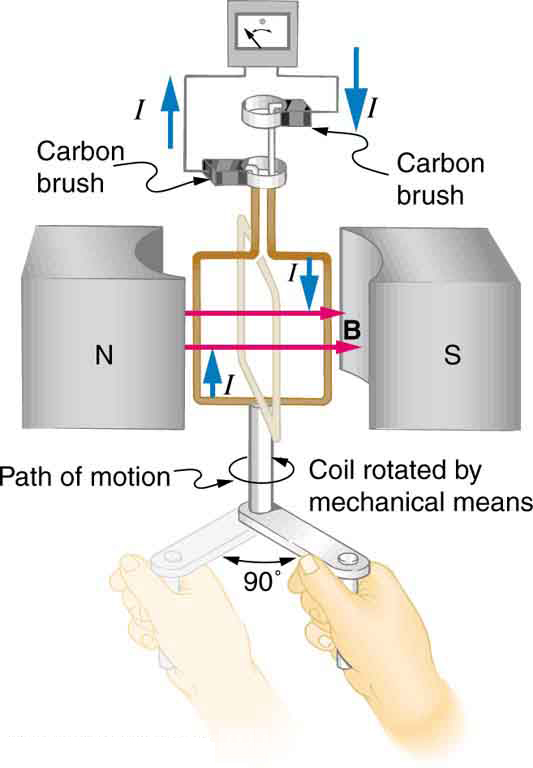
A figura mostra um diagrama esquemático de um gerador elétrico. Consiste em uma bobina retangular giratória colocada entre os dois pólos de um ímã permanente, mostrados como dois blocos retangulares curvados na lateral voltada para a bobina. O campo magnético B é mostrado apontando do Pólo Norte para o Pólo Sul. As duas extremidades dessa bobina estão conectadas aos dois pequenos anéis. As duas escovas de carbono condutor são mantidas pressionadas separadamente em ambos os anéis. A bobina é conectada a um eixo com uma alça na outra extremidade. As extremidades externas das duas escovas são conectadas ao galvanômetro. O eixo é girado mecanicamente do lado de fora por um ângulo de noventa graus, ou seja, uma quarta revolução, para girar a bobina dentro do campo magnético. É mostrado que uma corrente flui na bobina no sentido horário e o galvanômetro mostra uma deflexão para a esquerda. — Figura\(\PageIndex{1}\): Quando esta bobina do gerador é girada em um quarto de uma revolução, o fluxo magnético\(\Phi\) muda de seu máximo para zero, induzindo um emf.

Estratégia:

Usamos a lei de indução de Faraday para encontrar a média de emf induzida ao longo de um tempo\(\Delta t\):\[emf = -N\frac{\Delta \Phi}{\Delta t}.\label{23.6.1}\] sabemos disso\(N = 200\) e\(\Delta t = 15.0 ms\), portanto, devemos determinar a mudança no fluxo\(\Delta \Phi\) para encontrar emf.

Solução:

Como a área do loop e a intensidade do campo magnético são constantes, vemos que\[\Delta \Phi = \Delta \left(BA\cos{\theta}\right) = AB\Delta\left(\cos{\theta}\right).\label{23.6.2}\] Agora,\(\Delta \left(\cos{\theta}\right) = -1.0\), uma vez que foi dado,\(\theta\) vai\(0^{\circ}\) de\(90^{\circ}\) a. Portanto\(\Delta \Phi = -AB\), e\[emf = N\frac{AB}{\Delta t}.\label{23.6.3}\] A área do loop é\(A = \pi r^{2} = \left(3.14...\right)\left(0.0500 m\right)^{2} = 7.85 \times 10^{-3} m^{2}\). Inserir esse valor dá\[emf = 200\frac{\left(7.85 \times 10^{-3} m^{2} \right) \left(1.25 T\right)}{1.50 \times 10^{-3}s} = 131V.\]

Discussão:

Esse é um valor médio prático, semelhante aos 120 V usados na energia doméstica.

O emf calculado no exemplo é a média de mais de um quarto de uma revolução. O que é o emf em um determinado instante? Ela varia com o ângulo entre o campo magnético e uma perpendicular à bobina. Podemos obter uma expressão para emf em função do tempo considerando o emf mocional em uma bobina retangular rotativa de largura\(\w\) e altura\(l\) em um campo magnético uniforme, conforme ilustrado na Figura\(\PageIndex{2}\).

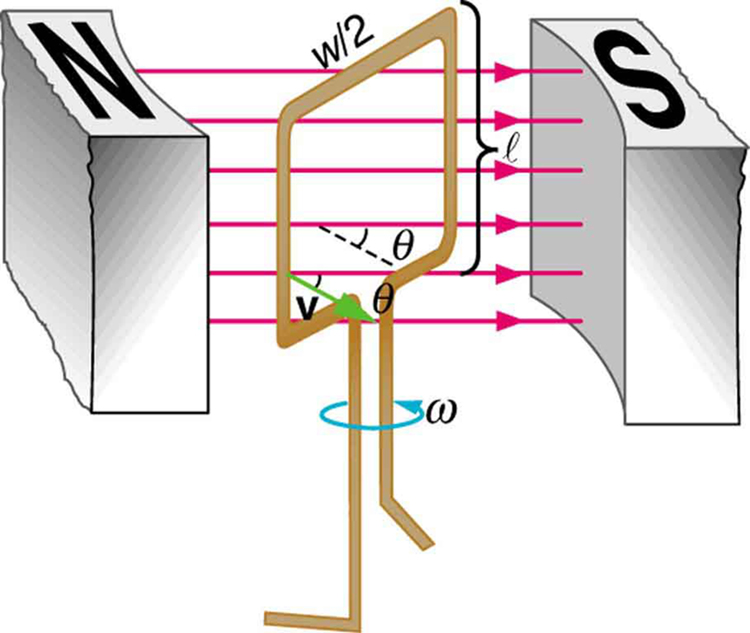
A figura mostra um diagrama esquemático de um gerador elétrico com uma única bobina retangular. A bobina retangular giratória é colocada entre os dois pólos de um ímã permanente, mostrados como dois blocos retangulares curvados na lateral voltada para a bobina. O campo magnético B é mostrado apontando do Pólo Norte para o Pólo Sul. O Pólo Norte está à esquerda e o Pólo Sul está à direita e, portanto, a direção do campo é da esquerda para a direita. A velocidade angular da bobina é dada como ômega. O vetor de velocidade v da bobina forma um ângulo teta com a direção do campo. — Figura\(\PageIndex{2}\): Um gerador com uma única bobina retangular girada a uma velocidade angular constante em um campo magnético uniforme produz um emf que varia senoidalmente no tempo. Observe que o gerador é semelhante a um motor, exceto que o eixo é girado para produzir uma corrente e não o contrário.

As cargas nos fios do circuito experimentam a força magnética, porque estão se movendo em um campo magnético. As cargas nos fios verticais experimentam forças paralelas ao fio, causando correntes. Mas aqueles nos segmentos superior e inferior sentem uma força perpendicular ao fio, que não causa corrente. Assim, podemos encontrar o emf induzido considerando apenas os fios laterais. A emf mocional é dada como sendo\(emf = Blv\), onde a velocidade\(v\) é perpendicular ao campo magnético\(B\). Aqui, a velocidade está em um ângulo\(\theta\) com\(B\), de modo que seu componente é perpendicular a\(B\) é\(v\sin{\theta}\) (Figura\(\PageIndex{2}\)). Assim, neste caso, o emf induzido em cada lado é\(emf = Blv\sin{\theta}\), e eles estão na mesma direção. O emf total ao redor do loop é então

\[emf = 2Blv\sin{\theta}.\label{23.6.4}\]

Essa expressão é válida, mas não fornece emf em função do tempo. Para encontrar a dependência temporal de emf, assumimos que a bobina gira a uma velocidade angular constante\(\omega\). O ângulo\(\theta\) está relacionado à velocidade angular por\(\theta = \omega t\), de modo que

\[ emf = 2Blv\sin{\omega t}.\label{23.6.5}\]

Agora, a velocidade linear\(v\) está relacionada à velocidade angular\(\omega\) por\(v=r\omega\). Aqui\(r = \omega /2\), para que\(v = \left(w/2\right)\omega\), e

\[emf = 2Bl\frac{w}{2} \omega \sin{\omega t} = \left(w\right)B \omega \sin{\omega t}.\label{23.6.6}\]

Observando que a área do loop é\(A = w\), e permitindo\(N\) loops, descobrimos que

\[emf = NAB \omega \sin{\omega t}\label{23.6.7}\]

é o emf induzido em uma bobina geradora de\(N\) curvas e área\(A\) girando a uma velocidade angular constante\(\omega\) em um campo magnético uniforme\(B\). Isso também pode ser expresso como

\[emf = emf_{0}\sin{\omega t},\label{23.6.8}\]

onde\[emf_{0} = NAB \omega \label{23.6.9}\] é o máximo (pico) emf. Observe que a frequência da oscilação é\(f = \omega / 2\pi\), e o período é\(T = 1/f = 2\pi / \omega\). \(\PageIndex{3}\)A figura mostra um gráfico de emf em função do tempo, e agora parece razoável que a tensão AC seja senoidal.

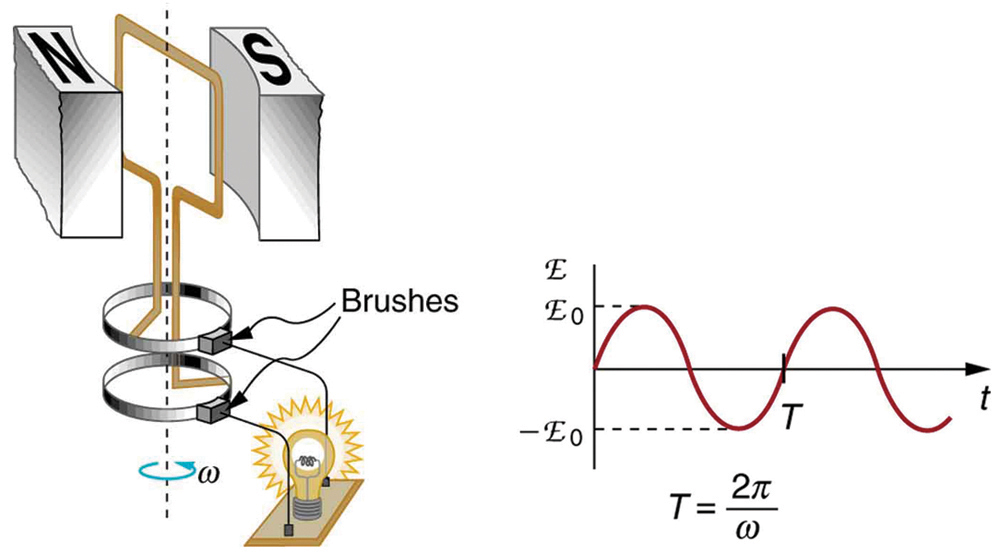
A primeira parte da figura mostra um diagrama esquemático de um gerador elétrico de bobina única. Consiste em um laço retangular giratório colocado entre os dois pólos de um ímã permanente, mostrado como dois blocos retangulares curvados na lateral voltada para o laço. O campo magnético B é mostrado apontando do Pólo Norte para o Pólo Sul. As duas extremidades desse loop estão conectadas aos dois pequenos anéis. As duas escovas de carbono condutor são mantidas pressionadas separadamente em ambos os anéis. O loop é girado no campo com um ômega de velocidade angular. As extremidades externas das duas escovas são conectadas a uma lâmpada elétrica que parece brilhar intensamente. A segunda parte da figura mostra o gráfico de E m f gerado em função do tempo t. O e m f está ao longo do eixo Y e o tempo t está ao longo do eixo X. O gráfico é uma onda senoidal progressiva com um período de tempo T. Os máximos da crista estão em E zero e os mínimos mínimos estão em E zero negativo. — Figura: O\(\PageIndex{3}\) emf de um gerador é enviado para uma lâmpada com o sistema de anéis e escovas mostrado. O gráfico fornece o emf do gerador em função do tempo. \(emf_0\)é o pico de emf. O período é\(T=1/f=2π/ω\), onde\(f\) está a frequência. Observe que o script E significa emf.

O fato de que o pico de emf\(emf_0=NABω\),, faz sentido. Quanto maior o número de bobinas, maior a área e quanto mais forte o campo, maior a tensão de saída. É interessante que quanto mais rápido o gerador é girado (maior ω), maior o emf. Isso é perceptível em geradores de bicicletas — pelo menos nas variedades mais baratas. Um dos autores, quando jovem, achou divertido andar de bicicleta rápido o suficiente para acender as luzes, até que ele teve que voltar para casa sem luz em uma noite escura.

A figura mostra um esquema pelo qual um gerador pode ser fabricado para produzir corrente contínua pulsada. Arranjos mais elaborados de várias bobinas e anéis divididos podem produzir uma corrente contínua mais suave, embora meios eletrônicos em vez de mecânicos sejam geralmente usados para produzir DC sem ondulações.

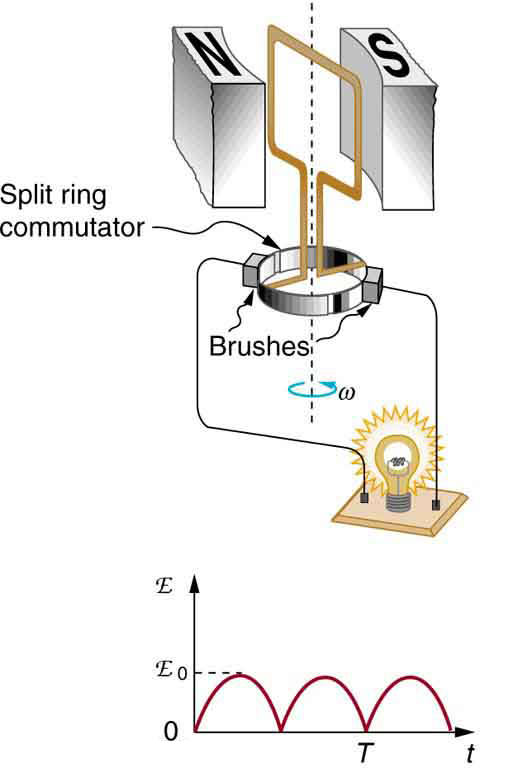
Figura\(\PageIndex{4}\): Anéis divididos, chamados de comutadores, produzem uma saída emf DC pulsada nesta configuração.

Exemplo\(\PageIndex{2}\): Calculating the Maximum Emf of a Generator

Calcule o máximo de emf, emf0, do gerador que foi objeto do Exemplo.

Estratégia

Uma vez que\(ω\) a velocidade angular, determinada,\(emf_0=NABω\) pode ser usada para encontrar\(emf_0\). Todas as outras quantidades são conhecidas.

Solução

A velocidade angular é definida como a mudança no ângulo por unidade de tempo:

\(ω=\frac{Δθ}{Δt}\).

Um quarto de uma revolução é\(π/2\) radianos e o tempo é 0,0150 s; portanto,

\(ω=\frac{π/2rad}{0.0150 s}=104.7 rad/s.\)

104,7 rad/s são exatamente 1000 rpm. Substituímos esse valor por ω e as informações do exemplo anterior em\(emf_0=NABω\), produzindo

\(emf_0=NABω=200(7.85×10^{−3}m^2)(1.25T)(104.7rad/s)=206V\).

Discussão

O emf máximo é maior do que o emf médio de 131 V encontrado no exemplo anterior, como deveria ser.

Na vida real, os geradores elétricos parecem muito diferentes dos números desta seção, mas os princípios são os mesmos. A fonte de energia mecânica que gira a bobina pode ser água caindo (energia hidrelétrica), vapor produzido pela queima de combustíveis fósseis ou a energia cinética do vento. \(\PageIndex{5}\)mostra uma visão cortante de uma turbina a vapor; o vapor se move sobre as pás conectadas ao eixo, que gira a bobina dentro do gerador.

Fotografia de uma turbina a vapor conectada a um gerador. — Figura\(\PageIndex{5}\): Gerador/turbina a vapor. O vapor produzido pela queima do carvão afeta as pás da turbina, girando o eixo que está conectado ao gerador. (crédito: Nabonaco, Wikimedia Commons)

Os geradores ilustrados nesta seção são muito parecidos com os motores ilustrados anteriormente. Isso não é coincidência. Na verdade, um motor se torna um gerador quando seu eixo gira. Certos automóveis antigos usavam seu motor de partida como gerador. Em Back Emf, exploraremos ainda mais a ação de um motor como gerador.

Resumo

Um gerador elétrico gira uma bobina em um campo magnético, induzindo um emf dado em função do tempo por

\(emf=NABωsinωt,\)

onde\(A\) é a área\(N\) de uma bobina giratória girada a uma velocidade angular constante ω em um campo magnético uniforme\(B\).

O pico emf\ (emf_0) de um gerador é

\(emf_0=NABω\).

Glossário

gerador elétrico: um dispositivo para converter trabalho mecânico em energia elétrica; induz um emf girando uma bobina em um campo magnético

emf induzido em uma bobina de gerador: \(emf=NABωsinωt\), onde\(A\) é a área\(N\) de uma bobina giratória girada a uma velocidade angular constante\(ω\) em um campo magnético uniforme\(B\), durante um período de tempo\(t\)

pico de emf: (EMF_0=NaBΩ\) 0 = N A B ω