Skip to main content
Global

21.1: Resistores em série e paralelos

  1. Last updated
  2. Save as PDF
  • Page ID
    194040

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Desenhe um circuito com resistores em paralelo e em série.
    • Calcule a queda de tensão de uma corrente em um resistor usando a lei de Ohm.
    • Compare a forma como a resistência total é calculada para resistores em série e em paralelo.
    • Explique por que a resistência total de um circuito paralelo é menor que a menor resistência de qualquer um dos resistores desse circuito.
    • Calcule a resistência total de um circuito que contém uma mistura de resistores conectados em série e em paralelo.

    A maioria dos circuitos tem mais de um componente, chamado de resistor, que limita o fluxo de carga no circuito. Uma medida desse limite no fluxo de carga é chamada de resistência. As combinações mais simples de resistores são as conexões em série e paralelas ilustradas na Figura\(\PageIndex{1}\). A resistência total de uma combinação de resistores depende de seus valores individuais e de como eles estão conectados.

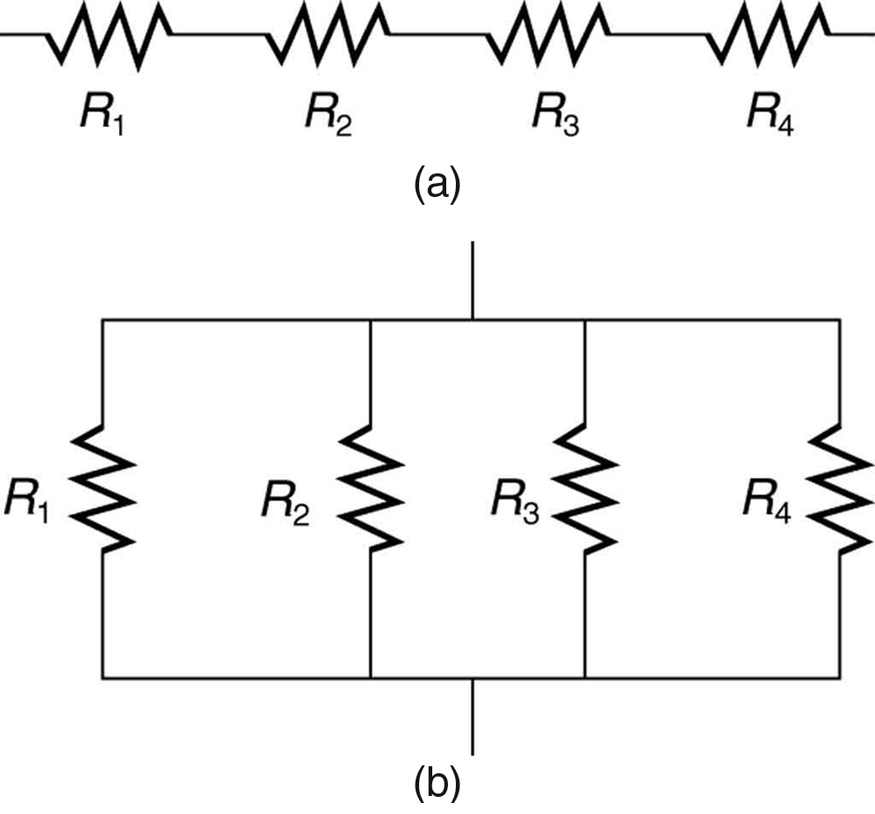
    Na parte a da figura, os resistores rotulados R sub 1, R sub 2, R sub 3 e R sub 4 são conectados em série ao longo de um caminho de um circuito. Na parte b da figura, os mesmos resistores são conectados ao longo de caminhos paralelos de um circuito.
    Figura\(\PageIndex{1}\): (a) Uma conexão em série de resistores. (b) Uma conexão paralela de resistores.

    Resistores em série

    Quando os resistores estão em série? Os resistores estão em série sempre que o fluxo de carga, chamado de corrente, deve fluir pelos dispositivos sequencialmente. Por exemplo, se a corrente flui através de uma pessoa segurando uma chave de fenda e para a Terra,\(R_{1}\) na Figura\(\PageIndex{1}\) (a) pode estar a resistência do eixo da chave de fenda,\(R_{2}\) a resistência de sua alça,\(R_{3}\) a resistência do corpo da pessoa e\(R_{4}\) a resistência de seus sapatos.

    A figura\(\PageIndex {2}\) mostra resistores em série conectados a uma fonte de tensão. Parece razoável que a resistência total seja a soma das resistências individuais, considerando que a corrente deve passar por cada resistor em sequência. (Esse fato seria uma vantagem para uma pessoa que desejasse evitar um choque elétrico, que poderia reduzir a corrente usando sapatos de borracha de alta resistência. Pode ser uma desvantagem se uma das resistências fosse um cabo de alta resistência defeituoso para um aparelho que reduziria a corrente de operação.)

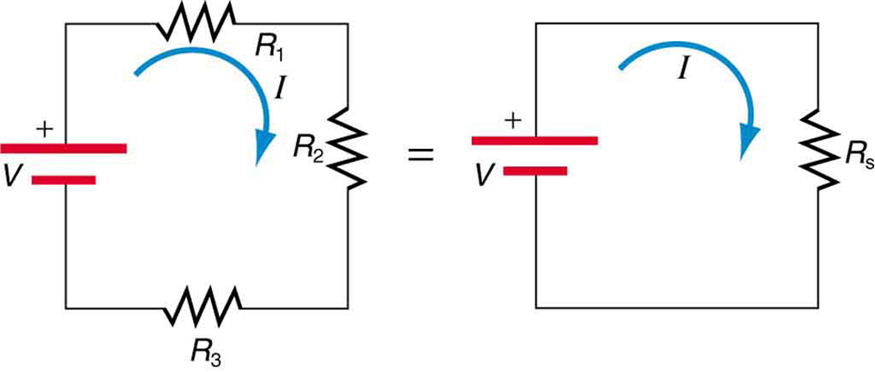
    Dois circuitos elétricos são comparados. O primeiro tem três resistores, R sub um, R sub dois e R sub três, conectados em série com uma fonte de tensão V para formar um circuito fechado. O primeiro circuito é equivalente ao segundo circuito, que tem um único resistor R sub s conectado a uma fonte de tensão V. Ambos os circuitos carregam uma corrente I, que começa na extremidade positiva da fonte de tensão e se move no sentido horário ao redor do circuito.
    Figura\(\PageIndex{2}\): Três resistores conectados em série a uma bateria (esquerda) e a resistência equivalente única ou em série (direita).

    Para verificar se as resistências em série realmente aumentam, vamos considerar a perda de energia elétrica, chamada de queda de tensão, em cada resistor na Figura\(\PageIndex {2}\).

    De acordo com a lei de Ohm, a queda de tensão\(V\),, através de um resistor quando uma corrente flui através dele é calculada usando a equação\(V=IR\), onde é\(I\) igual à corrente em amperes (A) e\(R\) é a resistência em ohms\((\Omega)\). Outra maneira de pensar nisso é que\(V\) é a tensão necessária para fazer uma corrente\(I\) fluir através de uma resistência\(R\).

    Então, a queda de tensão\(R_{1}\) é\(V_{1}=IR_{1}\), aquela do outro lado\(V_{2}=IR_{2}\), e aquela do outro lado\(R_{3}\) é\(V_{3}=IR_{3}\). A soma dessas tensões é igual à saída de tensão da fonte; ou seja,

    \[V=V_{1}+V_{2}+V_{3}.\]

    Essa equação é baseada na conservação de energia e conservação de carga. A energia potencial elétrica pode ser descrita pela equação\(\mathrm{PE}=qV\), onde\(q\) está a carga elétrica e\(V\) é a tensão. Assim, a energia fornecida pela fonte é\(qV\), enquanto a dissipada pelos resistores é

    \[qV_{1}+qV_{2}+qV_{3}.\]

    CONEXÃO: LEIS DE CONSERVAÇÃO

    As derivações das expressões para resistência em série e paralela são baseadas nas leis de conservação de energia e conservação de carga, que afirmam que a carga total e a energia total são constantes em qualquer processo. Essas duas leis estão diretamente envolvidas em todos os fenômenos elétricos e serão invocadas repetidamente para explicar os efeitos específicos e o comportamento geral da eletricidade.

    Essas energias devem ser iguais, porque não há outra fonte e nenhum outro destino de energia no circuito. Assim,\(qV=qV_{1}+qV_{2}+qV_{3}\). A cobrança é\(q\) cancelada, rendendo\(V=V_{1}+V_{2}+V_{3}\), conforme declarado. (Observe que a mesma quantidade de carga passa pela bateria e por cada resistor em um determinado período de tempo, pois não há capacitância para armazenar a carga, não há lugar para vazar a carga e a carga é conservada.)

    Agora, substituindo os valores das tensões individuais, obtém-se

    \[V=IR_{1}+IR_{2}+IR_{3}=I(R_{1}+R_{2}+R_{3}).\]

    Observe que, para a resistência equivalente de série única\(R_{\mathrm{S}}\), temos

    \[V=IR_{\mathrm{S}}.\]

    Isso implica que a resistência em série total ou equivalente\(R_{\mathrm{S}}\) de três resistores é\(R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}\).

    Essa lógica é válida em geral para qualquer número de resistores em série; portanto, a resistência total\(R_{\mathrm{S}}\) de uma conexão em série é

    \[R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}+\dots ,\]

    conforme proposto. Como toda a corrente deve passar por cada resistor, ela experimenta a resistência de cada uma, e as resistências em série simplesmente se somam.

    Exemplo\(\PageIndex{1}\): Calculating Resistance, Current, Voltage Drop, and Power Dissipation: Analysis of a Series Circuit

    Suponha que a saída de tensão da bateria na Figura\(\PageIndex{2}\) seja\(12.0\mathrm{V}\), e as resistências sejam\(R_{1}=1.00\Omega\)\(R_{2}=6.00\Omega\),\(R_{3}=13.0\Omega\) e. (a) Qual é a resistência total? (b) Encontre o atual. (c) Calcule a queda de tensão em cada resistor e mostre que esses acréscimos são iguais à saída de tensão da fonte. (d) Calcule a potência dissipada por cada resistor. (e) Encontre a potência de saída da fonte e mostre que ela é igual à potência total dissipada pelos resistores.

    Estratégia e solução para (a)

    A resistência total é simplesmente a soma das resistências individuais, conforme dada por esta equação:

    \[R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}\]

    \[=1.00\Omega + 6.00\Omega + 13.0\Omega\]

    \[=20.0 \Omega.\]

    Estratégia e solução para (b)

    A corrente é encontrada usando a lei de Ohm,\(V=IR\). Inserir o valor da tensão aplicada e a resistência total produz a corrente para o circuito:

    \[I=\dfrac{V}{R_{\mathrm{S}}}=\dfrac{12.0\Omega}{20.0\Omega}=0.600 \mathrm{A}.\]

    Estratégia e solução para (c)

    A voltagem — ou\(IR\) queda — em um resistor é dada pela lei de Ohm. Ao inserir a corrente e o valor da primeira resistência, obtém-se

    \[V_{1}=IR_{1}=(0.600\mathrm{A})(1.0\Omega)=0.600\mathrm{V}.\]

    Da mesma forma,

    \[V_{2}=IR_{2}=(0.600\mathrm{A})(6.0\Omega)=3.60\mathrm{V}\]

    e

    \[V_{3}=IR_{3}=(0.600\mathrm{A})(13.0\Omega)=7.80\mathrm{V}.\]

    Discussão para (c)

    As três\(IR\) gotas se somam\(12.0\mathrm{V}\), conforme previsto:

    \[V_{1}+V_{2}+V_{3}=(0.600+3.60+7.80)\mathrm{V}=12.0\mathrm{V}.\]

    Estratégia e solução para (d)

    A maneira mais fácil de calcular a potência em watts (W) dissipada por um resistor em um circuito DC é usar a lei de Joule,\(P=IV\), onde\(P\) está a energia elétrica. Nesse caso, cada resistor tem a mesma corrente total fluindo através dele. Ao substituir a lei de Ohm pela lei\(V=IR\) de Joule, obtemos a potência dissipada pelo primeiro resistor como

    \[P_{1}=I^{2}R_{1}=(0.600\mathrm{A})^{2}(1.00\Omega)=0.360 \mathrm{W}.\]

    Da mesma forma,

    \[P_{2}=I^{2}R_{2}=(0.600\mathrm{A})^{2}(6.00\Omega)=2.16 \mathrm{W}\]

    e

    \[P_{3}=I^{2}R_{3}=(0.600\mathrm{A})^{2}(13.0\Omega)=4.68\mathrm{W}.\]

    Discussão para (d)

    A energia também pode ser calculada usando\(P=IV\) ou\(P=\dfrac{V^{2}}{R}\) onde\(V\) está a queda de tensão no resistor (não a tensão total da fonte). Os mesmos valores serão obtidos.

    Estratégia e solução para (e)

    A maneira mais fácil de calcular a potência da fonte é usar\(P=IV\), onde\(V\) está a tensão da fonte. Isso dá

    \[P=(0.600\mathrm{A})(12.0\mathrm{V})=7.20 \mathrm{W}.\]

    Discussão para (e)

    Observe, coincidentemente, que a potência total dissipada pelos resistores também é de 7,20 W, a mesma que a potência emitida pela fonte. Ou seja,

    \[P_{1}+P_{2}+P_{3}=(0.360 +2.16+4.68)\mathrm{W}=7.20\mathrm{W}.\]

    Potência é energia por unidade de tempo (watts) e, portanto, a conservação de energia exige que a potência da fonte seja igual à potência total dissipada pelos resistores.

    PRINCIPAIS CARACTERÍSTICAS DOS RESISTORES EM SÉRIE

    1. As resistências em série adicionam:\(R_{\mathrm{S}}=R_{1}+R_{2}+R_{3}+\dots\)
    2. A mesma corrente flui através de cada resistor em série.
    3. Resistores individuais em série não obtêm a tensão total da fonte, mas a dividem.

    Resistores em paralelo

    A figura\(\PageIndex{3}\) mostra resistores em paralelo, conectados a uma fonte de tensão. Os resistores estão em paralelo quando cada resistor é conectado diretamente à fonte de tensão conectando fios com resistência insignificante. Cada resistor, portanto, tem a tensão total da fonte aplicada a ele.

    Cada resistor consome a mesma corrente que usaria se estivesse conectado sozinho à fonte de tensão (desde que a fonte de tensão não esteja sobrecarregada). Por exemplo, os faróis, o rádio e assim por diante de um automóvel são conectados em paralelo, para que utilizem a voltagem total da fonte e possam operar de forma totalmente independente. O mesmo acontece em sua casa ou em qualquer prédio. (Veja a Figura\(\PageIndex{3}\) (b).)

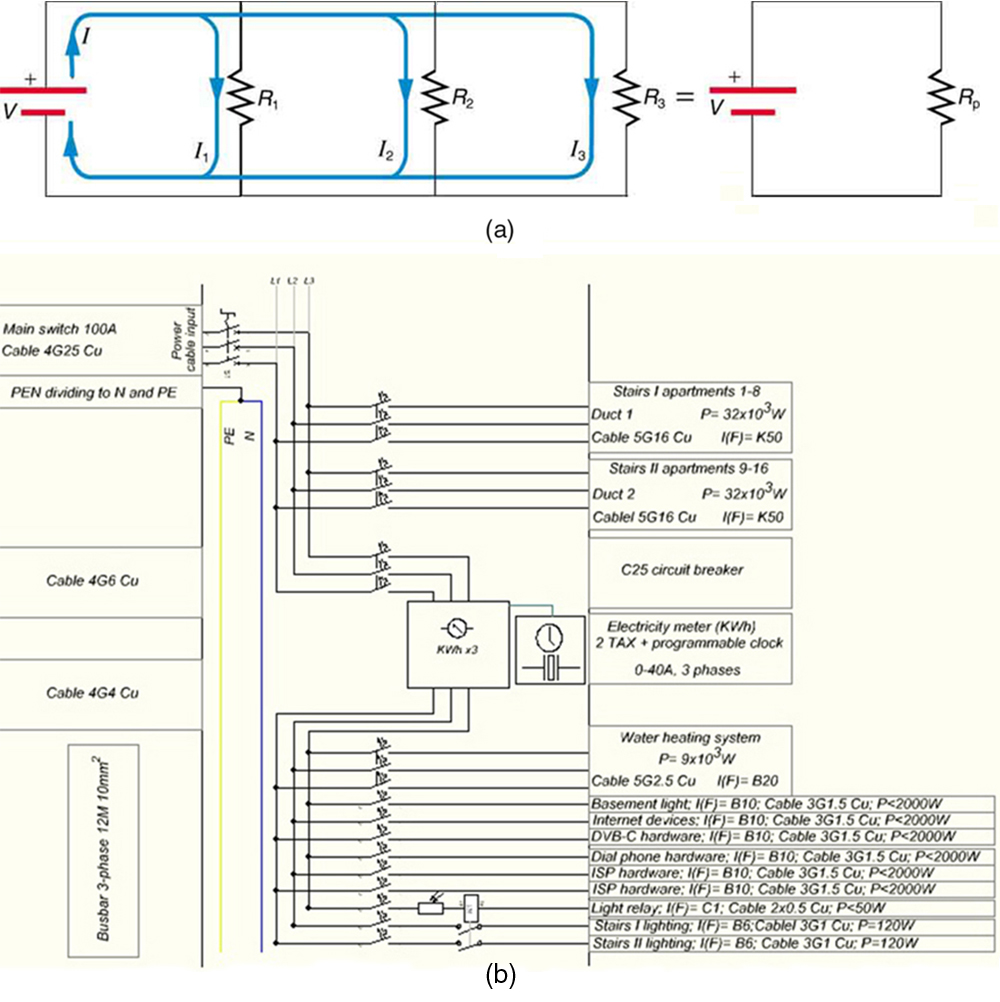
    A parte a mostra dois circuitos elétricos que são comparados. O primeiro circuito elétrico é organizado com resistores em paralelo. O circuito tem três caminhos, com uma fonte de tensão V em uma extremidade. Logo após a fonte de tensão, o circuito tem corrente I. O primeiro caminho tem resistor R sub um e corrente I sub um após o resistor. O segundo caminho tem resistor R sub dois e corrente I sub dois após o resistor. O terceiro caminho tem resistor R sub três com corrente I sub três após o resistor. O primeiro circuito é equivalente ao segundo circuito. O segundo circuito tem uma fonte de tensão V e uma resistência paralela equivalente R sub p. A parte b mostra um diagrama de fiação elétrica complicado de uma placa de distribuição que fornece eletricidade para uma casa.
    Figura\(\PageIndex{3}\): (a) Três resistores conectados em paralelo a uma bateria e a resistência equivalente única ou paralela. (b) Configuração de energia elétrica em uma casa. (crédito: Dmitry G, Wikimedia Commons)

    Para encontrar uma expressão para a resistência paralela equivalente\(R_{\mathrm{p}}\), vamos considerar as correntes que fluem e como elas estão relacionadas à resistência. Como cada resistor no circuito tem a tensão total, as correntes que fluem através dos resistores individuais são\(I_{1}=\dfrac{V}{R_{1}}\)\(I_{2}=\dfrac{V}{R_{2}}\),\(I_{3}=\dfrac{V}{R_{3}}\) e. A conservação da carga implica que a corrente total\(I\) produzida pela fonte é a soma dessas correntes:

    \[I=I_{1}+I_{2}+I_{3}.\]

    Substituindo as expressões pelas correntes individuais dá

    \[I=\dfrac{V}{R_{1}}+\dfrac{V}{R_{2}}+\dfrac{V}{R_{3}}=V(\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{R_{3}}).\]

    Observe que a lei de Ohm para a resistência única equivalente fornece

    \[I=\dfrac{V}{R_{\mathrm{p}}}=V(\dfrac{1}{R_{\mathrm{p}}}).\]

    Os termos dentro dos parênteses nas duas últimas equações devem ser iguais. Generalizando para qualquer número de resistores, a resistência total\(R_{\mathrm{p}}\) de uma conexão paralela está relacionada às resistências individuais por

    \[\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{R_{3}}+\dots\]

    Essa relação resulta em uma resistência total menor\(R_{\mathrm{p}}\) que a menor das resistências individuais. (Isso é visto no próximo exemplo.) Quando os resistores são conectados em paralelo, mais corrente flui da fonte do que fluiria para qualquer um deles individualmente e, portanto, a resistência total é menor.

    Exemplo\(\PageIndex{2}\): Calculating Resistance, Current, Power Dissipation, and Power Output: Analysis of a Parallel Circuit

    Deixe a saída de tensão da bateria e as resistências na conexão paralela na Figura\(\PageIndex{3}\) serem as mesmas da conexão em série considerada anteriormente:\(V=12.0\mathrm{V},\: R_{1}=1.00\Omega,\: R_{2}=6.00\Omega\),\(R_{3}=13.0\Omega\) e. (a) Qual é a resistência total? (b) Encontre a corrente total. (c) Calcule as correntes em cada resistor e mostre que essas somas equivalem à saída total de corrente da fonte. (d) Calcule a potência dissipada por cada resistor. (e) Encontre a potência de saída da fonte e mostre que ela é igual à potência total dissipada pelos resistores.

    Estratégia e solução para (a)

    A resistência total para uma combinação paralela de resistores é encontrada usando a equação abaixo. A inserção de valores conhecidos fornece

    \[\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{R_{3}}=\dfrac{1}{1.00\Omega}+\dfrac{1}{6.00\Omega}+\dfrac{1}{13.0\Omega}.\]

    Assim,

    \[\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1.00}{\Omega}+\dfrac{0.1667}{\Omega}+\dfrac{0.07692}{\Omega}=\dfrac{1.2436}{\Omega}.\]

    (Observe que nesses cálculos, cada resposta intermediária é mostrada com um dígito extra.)

    Devemos inverter isso para encontrar a resistência total\(R_{\mathrm{p}}\). Isso rende

    \[R_{\mathrm{p}}=\dfrac{1}{1.2436}\Omega=0.8041\Omega.\]

    A resistência total com o número correto de dígitos significativos é\(R_{\mathrm{p}}=0.804\Omega\).

    Discussão para (a)

    \(R_{\mathrm{p}}\)é, como previsto, menor do que a menor resistência individual.

    Estratégia e solução para (b)

    A corrente total pode ser encontrada na lei de Ohm, substituindo\(R_{\mathrm{p}}\) a resistência total. Isso dá

    \[I=\dfrac{V}{R_{\mathrm{p}}}=\dfrac{12.0\mathrm{V}}{0.8041 \Omega}=14.92 \mathrm{A}.\]

    Discussão para (b)

    A corrente\(i\) para cada dispositivo é muito maior do que para os mesmos dispositivos conectados em série (veja o exemplo anterior). Um circuito com conexões paralelas tem uma resistência total menor do que os resistores conectados em série.

    Estratégia e solução para (c)

    As correntes individuais são facilmente calculadas a partir da lei de Ohm, pois cada resistor recebe a tensão total. Assim,

    \[I_{1}=\dfrac{V}{R_{1}}=\dfrac{12.0\mathrm{V}}{1.00\Omega}=12.0\mathrm{A}.\]

    Da mesma forma,

    \[I_{2}=\dfrac{V}{R_{2}}=\dfrac{12.0\mathrm{V}}{6.00\Omega}=2.00\mathrm{A}\]

    e

    \[I_{3}=\dfrac{V}{R_{3}}=\dfrac{12.0\mathrm{V}}{13.0\Omega}=0.92\mathrm{A}.\]

    Discussão para (c)

    A corrente total é a soma das correntes individuais:

    \[I_{1}+I_{2}+I_{3}=14.92\mathrm{A}.\]

    Isso é consistente com a conservação da carga.

    Estratégia e solução para (d)

    A potência dissipada por cada resistor pode ser encontrada usando qualquer uma das equações que relacionam potência à corrente, tensão e resistência, já que todas as três são conhecidas. Vamos usar\(P=\dfrac{V^{2}}{R}\), já que cada resistor recebe tensão total. Assim,

    \[P_{1}=\dfrac{V^{2}}{R_{1}}=\dfrac{(12.0\mathrm{V})^{2}}{1.00\Omega}=144\mathrm{W}.\]

    Da mesma forma,

    \[P_{2}=\dfrac{V^{2}}{R_{2}}=\dfrac{(12.0\mathrm{V})^{2}}{6.00\Omega}=24.0\mathrm{W}\]

    e

    \[P_{3}=\dfrac{V^{2}}{R_{3}}=\dfrac{(12.0\mathrm{V})^{2}}{13.0\Omega}=11.1\mathrm{W}.\]

    Discussão para (d)

    A potência dissipada por cada resistor é consideravelmente maior em paralelo do que quando conectada em série à mesma fonte de tensão.

    Estratégia e solução para (e)

    A potência total também pode ser calculada de várias maneiras. Escolher\(P=IV\) e inserir o total atual de rendimentos

    \[P=IV=(14.92\mathrm{A})(12.0\mathrm{V})=179\mathrm{W}.\]

    Discussão para (e)

    A potência total dissipada pelos resistores também é de 179 W:

    \[P_{1}+P_{2}+P_{3}=144\mathrm{W}+24.0\mathrm{W}+11.1\mathrm{W}=179\mathrm{W}.\]

    Isso é consistente com a lei de conservação de energia.

    Discussão geral

    Observe que tanto as correntes quanto as potências nas conexões paralelas são maiores do que as dos mesmos dispositivos em série.

    PRINCIPAIS CARACTERÍSTICAS DOS RESISTORES EM PARALELO

    1. A resistência paralela é encontrada e é menor do que qualquer resistência individual na combinação.\(\dfrac{1}{R_{\mathrm{p}}}=\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{R_{3}}+\dots\)
    2. Cada resistor em paralelo tem a mesma tensão total da fonte aplicada a ele. (Os sistemas de distribuição de energia geralmente usam conexões paralelas para fornecer a infinidade de dispositivos atendidos com a mesma voltagem e permitir que eles operem de forma independente.)
    3. Nem todos os resistores paralelos obtêm a corrente total; eles a dividem.

    Combinações de séries e paralelas

    Conexões mais complexas de resistores às vezes são apenas combinações de séries e paralelas. Eles são comumente encontrados, especialmente quando a resistência do fio é considerada. Nesse caso, a resistência do fio está em série com outras resistências que estão em paralelo.

    Combinações de série e paralelo podem ser reduzidas a uma única resistência equivalente usando a técnica ilustrada na Figura\(\PageIndex{4}\). Várias peças são identificadas como em série ou paralelas, reduzidas a seus equivalentes e ainda mais reduzidas até que reste uma única resistência. O processo é mais demorado do que difícil.

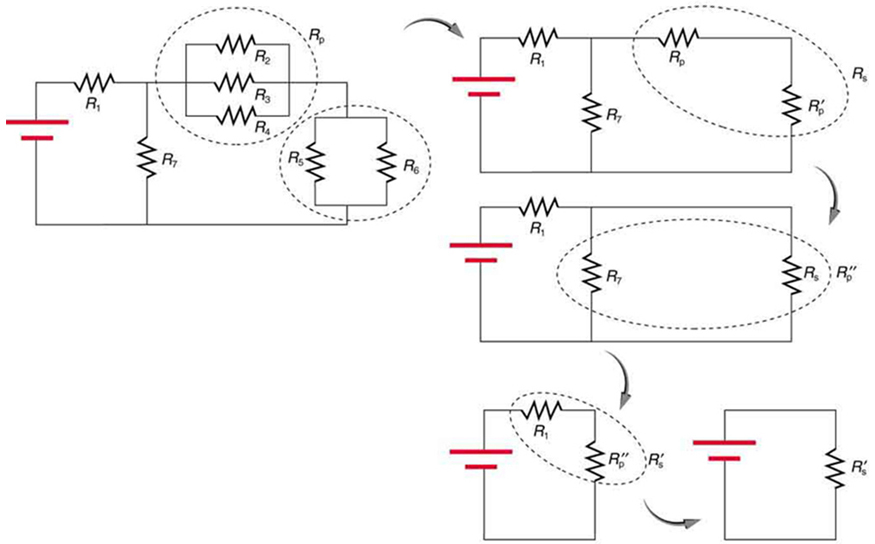
    O diagrama tem um conjunto de cinco circuitos. O primeiro circuito tem uma combinação de sete resistores em série e combinações paralelas. Possui um resistor R sub um em série com um conjunto de três resistores R sub dois, R sub três e R sub quatro em paralelo e conectados em série com uma combinação de resistores R sub cinco e R sub seis, que são paralelos. Um resistor R sub sete é conectado em paralelo ao R sub um e à fonte de tensão. O segundo circuito calcula combinações de todos os resistores paralelos no circuito um e os substitui por sua resistência equivalente. Tem um resistor R sub one em série com R sub p e R sub p prime. Um resistor R sub sete é conectado em paralelo ao R sub um e à fonte de tensão. O terceiro circuito pega a combinação dos resistores em série R sub p e R sub p prime e a substitui por R sub s. Ele tem um resistor R sub um em série com R sub s. Um resistor R sub sete é conectado em paralelo a R sub s e à fonte de tensão. O quarto circuito mostra uma combinação paralela de R sub sete e R sub s são calculados e substituídos por R sub p double prime. O circuito agora tem uma fonte de tensão combinada em série, R sub um e R sub p double prime. O quinto circuito mostra o equivalente final do primeiro circuito. Ele tem uma fonte de tensão conectada através de uma resistência equivalente final R sub s prime.
    Figura\(\PageIndex{4}\): Essa combinação de sete resistores tem peças em série e paralelas. Cada um é identificado e reduzido a uma resistência equivalente, e estes são ainda mais reduzidos até que uma única resistência equivalente seja alcançada.

    A combinação mais simples de resistência em série e paralela, mostrada na Figura\(\PageIndex{5}\), também é a mais instrutiva, pois é encontrada em muitas aplicações. Por exemplo,\(R_{1}\) pode ser a resistência dos fios de uma bateria de carro aos seus dispositivos elétricos, que estão em paralelo. \(R_{2}\)e\(R_{3}\) pode ser o motor de partida e uma luz do compartimento de passageiros. Anteriormente, presumimos que a resistência do fio é insignificante, mas, quando não é, tem efeitos importantes, como indica o próximo exemplo.

    Exemplo\(\PageIndex{3}\): Calculating Resistance, \(IR\) Drop, Current, and Power Dissipation: Combining Series and Parallel Circuits

    A figura\(\PageIndex{5}\) mostra os resistores dos dois exemplos anteriores conectados de uma maneira diferente — uma combinação de série e paralelo. Podemos considerar\(R_1\) a resistência dos fios que levam a\(R_2\)\(R_3\) e. (a) Encontre a resistência total. (b) Qual é a\(IR\) queda\(R_1\)? (c) Encontre a corrente\(I_2\) por meio de\(R_2\). (d) Por qual energia é dissipada\(R_2\)?

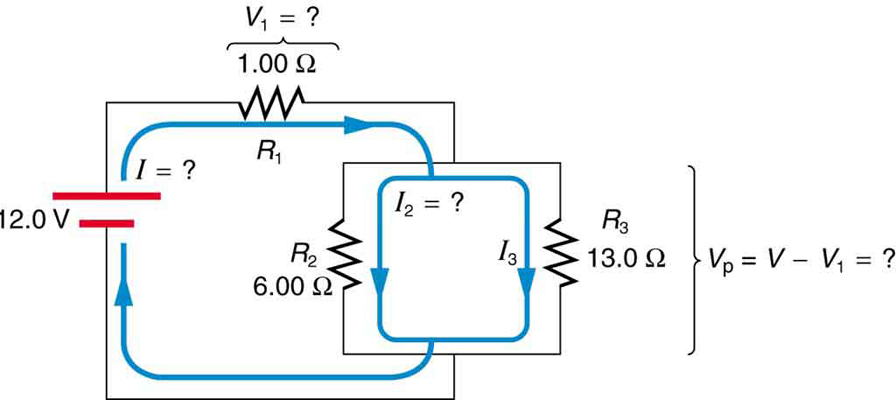
    Diagrama de circuito no qual uma bateria de doze pontos zero volts é conectada a uma combinação de três resistores. Os resistores R sub dois e R sub três são conectados em paralelo um ao outro, e sua combinação é conectada em série ao resistor R sub um. R sub um tem uma resistência de um ponto zero zero ohms, R sub dois tem uma resistência de seis pontos zero zero ohms, e R sub três tem uma resistência de treze ponto zero ohms.
    Figura\(\PageIndex{5}\). Esses três resistores são conectados a uma fonte de tensão para que\(R_2\)\(R_3\) estejam paralelos entre si e essa combinação esteja em série com\(R_1\).

    Estratégia e solução para (a)

    Para encontrar a resistência total, notamos que\(R_2\)\(R_3\) estão em paralelo e sua combinação\(R_p\) está em série com\(R_1\). Assim, a resistência total (equivalente) dessa combinação é\[R_{tot} = R_1 + R_2.\]

    Primeiro, descobrimos o\(R_p\) uso da equação para resistores em paralelo e inserindo valores conhecidos:\[\dfrac{1}{R_p} = \dfrac{1}{R_2} + \dfrac{1}{6.00 \, \Omega} + \dfrac{1}{13.0 \, \Omega} = \dfrac{0.2436}{\Omega}.\]

    A inversão dá\[R_p = \dfrac{1}{0.2436}\Omega = 4.11 \, \Omega.\] Então, a resistência total é\[R_{tot} = R_1 + R_p = 1.00 \Omega + 4.11 \Omega = 5.11 \, \Omega.\]

    Discussão para (a)

    A resistência total dessa combinação é intermediária entre a série pura e os valores paralelos puros (\(20.0 \, \Omega\)e\(0.804 \, \Omega\), respectivamente) encontrados para os mesmos resistores nos dois exemplos anteriores.

    Estratégia e solução para (b)

    Para encontrar a\(IR\) queda\(R_1\), notamos que toda a corrente\(I\) flui\(R_1\). Portanto, sua\(IR\) queda é\[V_1 = IR_1.\] Devemos encontrar\(I\) antes de podermos calcular\(V_1\). A corrente total\(I\) é encontrada usando a lei de Ohm para o circuito. Ou seja,\[I = \dfrac{V}{R_{tot}} = \dfrac{12.0 \, V}{5.11 \, \Omega} = 2.35 \, A.\] inserindo isso na expressão acima, obtemos\[V_1 = IR_1 = (2.35 \, A)(1.00 \, \Omega) = 2.35 \, V.\]

    Discussão para (b)

    A tensão aplicada\(R_2\) e\(R_3\) é menor que a tensão total em uma quantidade\(V_1\). Quando a resistência do fio é grande, ela pode afetar significativamente a operação dos dispositivos representados por\(R_2\)\(R_3\) e.

    Estratégia e solução para (c)

    Para encontrar a corrente\(R_2\), precisamos primeiro encontrar a tensão aplicada a ela. Chamamos essa tensão\(V_p\), porque ela é aplicada a uma combinação paralela de resistores. A tensão aplicada a ambos\(R_2\)\(R_3\) é reduzida pela quantidade\(V_1\), e assim é.\[V_p = V - V_1 = 12.0 \, V - 2.35 \, V = 9.65 \, V.\] Agora, a corrente\(I_2\) através da resistência\(R_2\) é encontrada usando a lei de Ohm:\[I_2 = \dfrac{V_p}{R_2} = \dfrac{9.65 \, V}{6.00 \, \Omega} = 1.61 \, A.\]

    Discussão para (c)

    A corrente é menor que os 2,00 A que fluíram\(R_2\) quando ela foi conectada em paralelo à bateria no exemplo anterior de circuito paralelo.

    Estratégia e solução para (d)

    A potência dissipada por\(R_2\) é dada por\[P_2 = (I_2)^2 R_2 = (1 61 \, A)^2(6.00 \, \Omega) = 15.5 \, W.\]

    Discussão para (d)

    A potência é menor que os 24,0 W que esse resistor dissipou quando conectado em paralelo à fonte de 12,0 V.

    Implicações práticas

    Uma implicação desse último exemplo é que a resistência nos fios reduz a corrente e a potência fornecidas a um resistor. Se a resistência do fio for relativamente grande, como em um cabo de extensão gasto (ou muito longo), essa perda pode ser significativa. Se uma grande corrente for consumida, a\(IR\) queda nos fios também pode ser significativa.

    Por exemplo, quando você está mexendo na geladeira e o motor liga, a luz da geladeira diminui momentaneamente. Da mesma forma, você pode ver a luz do compartimento de passageiros escurecer ao ligar o motor do seu carro (embora isso possa ser devido à resistência dentro da própria bateria).

    O que está acontecendo nessas situações de alta corrente é ilustrado na Figura\(\PageIndex{6}\). O dispositivo representado por\(R_3\) tem uma resistência muito baixa e, portanto, quando é ligado, uma grande corrente flui. Esse aumento de corrente causa uma\(IR\) queda maior nos fios representados pela\(R_1\) redução da tensão na lâmpada (ou seja\(R_2\)), que então escurece visivelmente.

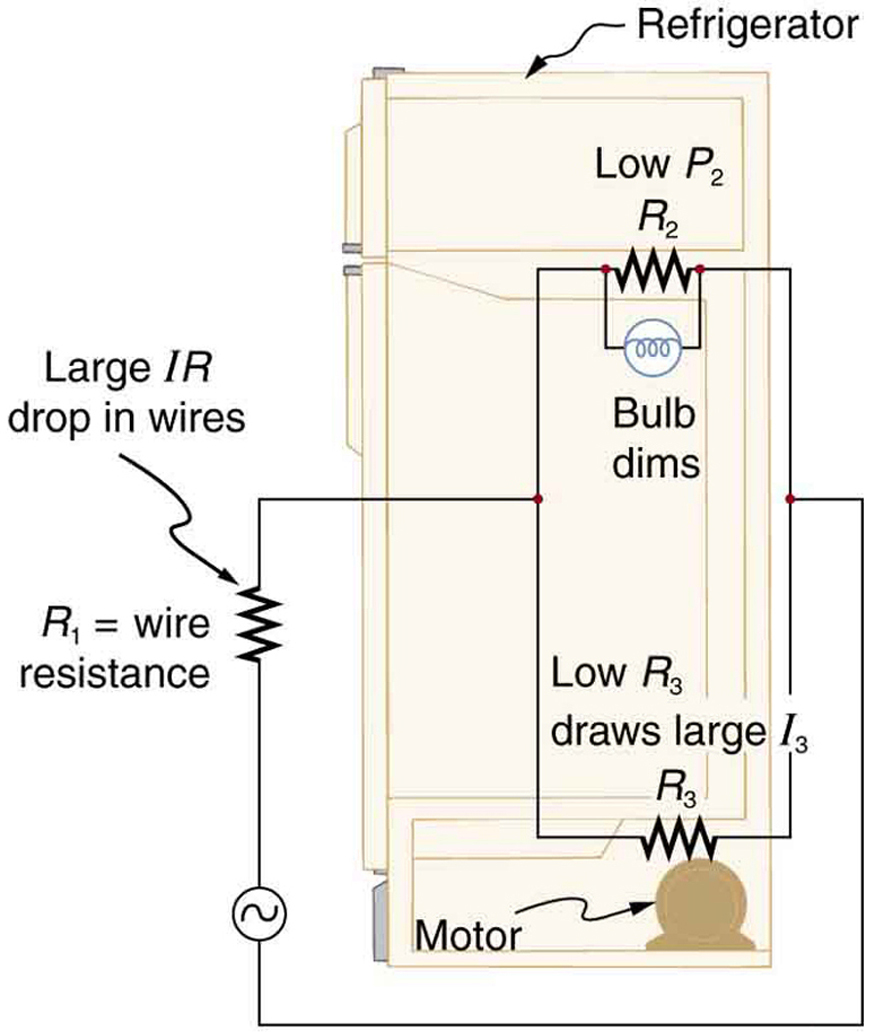
    Um desenho conceitual que mostra uma geladeira com seu motor e lâmpadas conectadas a um circuito A C doméstico por meio de um fio com resistência de R sub um. A lâmpada tem uma resistência R sub dois, e o motor tem uma resistência R sub três.
    Figura\(\PageIndex{6}\): Por que as luzes diminuem quando um aparelho grande é ligado? A resposta é que a grande corrente que o motor do aparelho consome causa uma\(IR\) queda significativa nos fios e reduz a tensão na luz.

    Exercício\(\PageIndex{1}\)

    Qualquer combinação arbitrária de resistores pode ser dividida em combinações em série e paralelas? Veja se você pode desenhar um diagrama de circuito de resistores que não pode ser dividido em combinações de série e paralelo.

    Responda

    Não, existem muitas maneiras de conectar resistores que não são combinações de série e paralelo, incluindo loops e junções. Nesses casos, as regras de Kirchhoff, a serem introduzidas nas Regras de Kirchhoff, permitirão que você analise o circuito.

    Estratégias de resolução de problemas para resistores em série e paralelos

    1. Desenhe um diagrama de circuito claro, rotulando todos os resistores e fontes de tensão. Esta etapa inclui uma lista dos conhecidos para o problema, pois eles estão rotulados em seu diagrama de circuito.
    2. Identifique exatamente o que precisa ser determinado no problema (identifique as incógnitas). Uma lista escrita é útil.
    3. Determine se os resistores estão em série, paralelos ou uma combinação de séries e paralelos. Examine o diagrama do circuito para fazer essa avaliação. Os resistores estão em série se a mesma corrente precisar passar sequencialmente por eles.
    4. Use a lista apropriada dos principais recursos para conexões em série ou paralelas para resolver as incógnitas. Há uma lista para séries e outra para paralelas. Se o problema tiver uma combinação de série e paralelo, reduza-o em etapas considerando grupos individuais de conexões em série ou paralelas, conforme feito neste módulo e nos exemplos. Nota especial: Ao encontrar\(R_p\), o recíproco deve ser tomado com cuidado.
    5. Verifique se as respostas são razoáveis e consistentes. Unidades e resultados numéricos devem ser razoáveis. A resistência total em série deve ser maior, enquanto a resistência paralela total deve ser menor, por exemplo. A potência deve ser maior para os mesmos dispositivos em paralelo em comparação com a série, e assim por diante.

    Resumo

    • A resistência total de um circuito elétrico com resistores conectados em série é a soma das resistências individuais:\(R_s = R_1 + R_2 + R_3 + ....\)
    • Cada resistor em um circuito em série tem a mesma quantidade de corrente fluindo através dele.
    • A queda de tensão, ou dissipação de energia, em cada resistor individual em uma série é diferente, e seu total combinado soma a entrada da fonte de alimentação.
    • A resistência total de um circuito elétrico com resistores conectados em paralelo é menor que a menor resistência de qualquer um dos componentes e pode ser determinada usando a fórmula:\(\dfrac{1}{R_p} = \dfrac{1}{R_1} +\dfrac{1}{R_2} + \dfrac{1}{R_3} + ....\)
    • Cada resistor em um circuito paralelo tem a mesma voltagem total da fonte aplicada a ele.
    • A corrente que passa por cada resistor em um circuito paralelo é diferente, dependendo da resistência.
    • Se uma conexão mais complexa de resistores for uma combinação de série e paralelo, ela poderá ser reduzida a uma única resistência equivalente identificando suas várias partes como em série ou paralelas, reduzindo cada uma a sua equivalente e continuando até que uma única resistência seja finalmente alcançada.

    Glossário

    série
    uma sequência de resistores ou outros componentes conectados a um circuito, um após o outro
    resistor
    um componente que fornece resistência à corrente que flui através de um circuito elétrico
    resistência
    causando uma perda de energia elétrica em um circuito
    Lei de Ohm
    a relação entre corrente, tensão e resistência dentro de um circuito elétrico: V = IR
    voltagem
    a energia potencial elétrica por unidade de carga; pressão elétrica criada por uma fonte de energia, como uma bateria
    queda de tensão
    a perda de energia elétrica à medida que uma corrente viaja através de um resistor, fio ou outro componente
    atual
    o fluxo de carga através de um circuito elétrico após um determinado ponto de medição
    Lei de Joule
    a relação entre potência elétrica potencial, tensão e resistência em um circuito elétrico, dada por:\(P_e = IV\)
    paralelo
    a fiação de resistores ou outros componentes em um circuito elétrico, de modo que cada componente receba uma tensão igual da fonte de alimentação; geralmente retratado em um diagrama em forma de escada, com cada componente em um degrau da escada