19.E: Exercícios
- Page ID
- 194777
Perguntas conceituais
19.1: Energia potencial elétrica: diferença de potencial
1. Tensão é a palavra comum para diferença de potencial. Qual termo é mais descritivo, diferença de voltagem ou potencial?
2. Se a tensão entre dois pontos for zero, uma carga de teste pode ser movida entre eles sem nenhum trabalho de rede sendo feito? Isso pode necessariamente ser feito sem exercer força? Explique.
3. Qual é a relação entre tensão e energia? Mais precisamente, qual é a relação entre diferença de potencial e energia potencial elétrica?
4. As voltagens são sempre medidas entre dois pontos. Por quê?
5. Como as unidades de volts e elétron-volts estão relacionadas? Como eles diferem?
19.2: Potencial elétrico em um campo elétrico uniforme
6. Discuta como a diferença de potencial e a intensidade do campo elétrico estão relacionadas. Dê um exemplo.
7. Qual é a força do campo elétrico em uma região onde o potencial elétrico é constante?
8. Uma carga negativa, inicialmente em repouso, se moverá em direção a um potencial maior ou menor? Explique o porquê.
19.3: Potencial elétrico devido a uma carga pontual
9. Em que região do espaço o potencial devido a uma esfera uniformemente carregada é o mesmo de uma carga pontual? Em que região ela difere daquela de uma cobrança pontual?
10. O potencial de uma esfera com carga não uniforme pode ser o mesmo de uma carga pontual? Explique.
19.4: Linhas equipotenciais
11. O que é uma linha equipotencial? O que é uma superfície equipotencial?
12. Explique com suas próprias palavras por que linhas e superfícies equipotenciais devem ser perpendiculares às linhas de campo elétrico.
13. Diferentes linhas equipotenciais podem se cruzar? Explique.
19.5: Capacitores e dielétricos
14. A capacitância de um dispositivo depende da tensão aplicada? E a carga armazenada nela?
15. Use as características da força de Coulomb para explicar por que a capacitância deve ser proporcional à área da placa de um capacitor. Da mesma forma, explique por que a capacitância deve ser inversamente proporcional à separação entre as placas.
16. Dê a razão pela qual um material dielétrico aumenta a capacitância em comparação com o que seria com o ar entre as placas de um capacitor. Qual é a razão independente pela qual um material dielétrico também permite que uma voltagem maior seja aplicada a um capacitor? (O dielétrico, portanto, aumenta\(C\) e permite um maior\(V\).)
17. Como o caráter polar das moléculas de água ajuda a explicar a constante dielétrica relativamente grande da água? (Figura)
18. Faíscas ocorrerão entre as placas de um capacitor cheio de ar em tensão mais baixa quando o ar estiver úmido do que quando seco. Explique o porquê, considerando o caráter polar das moléculas de água.
19. A água tem uma grande constante dielétrica, mas raramente é usada em capacitores. Explique o porquê.
20. Membranas em células vivas, incluindo aquelas em humanos, são caracterizadas por uma separação de carga através da membrana. Efetivamente, as membranas são, portanto, capacitores carregados com funções importantes relacionadas à diferença de potencial na membrana. A energia é necessária para separar essas cargas nas membranas vivas e, em caso afirmativo, sua fonte é a metabolização da energia alimentar ou alguma outra fonte?
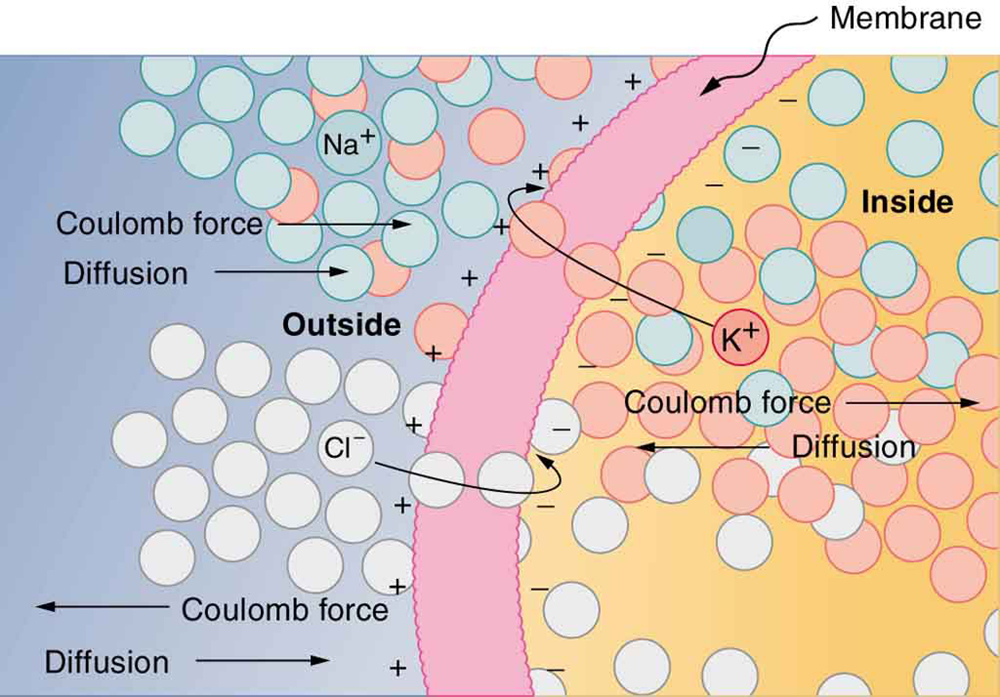
Figura 19.6.9: A membrana semipermeável de uma célula tem diferentes concentrações de íons por dentro e por fora. A difusão move os íons\(\mathrm{K}^{+}\) (potássio) e\(mathrm{Cl}^{-}\) (cloreto) nas direções mostradas, até que a força de Coulomb interrompa a transferência adicional. Isso resulta em uma camada de carga positiva na parte externa, uma camada de carga negativa na parte interna e, portanto, uma tensão na membrana celular. A membrana é normalmente impermeável a\(\mathrm{NA}^{+}\) (íons de sódio).
19.6: Capacitores em série e paralelos
21. Se você deseja armazenar uma grande quantidade de energia em um banco de capacitores, conectaria capacitores em série ou em paralelo? Explique.
19.7: Energia armazenada em capacitores
22. Como a energia contida em um capacitor carregado muda quando um dielétrico é inserido, supondo que o capacitor esteja isolado e sua carga seja constante? Isso implica que o trabalho foi feito?
23. O que acontece com a energia armazenada em um capacitor conectado a uma bateria quando um dielétrico é inserido? O trabalho foi realizado no processo?
Problemas e exercícios
19.1: Energia potencial elétrica: diferença de potencial
24. Encontre a razão entre as velocidades de um elétron e um íon de hidrogênio negativo (um com um elétron extra) acelerado pela mesma voltagem, assumindo velocidades finais não relativísticas. Pegue a massa do íon hidrogênio em si\(1.67\times 10^{-27}\: \mathrm{kg}\).
Solução
\(42.8\)
25. Um tubo evacuado usa uma tensão acelerada de 40 kV para acelerar os elétrons a atingirem uma placa de cobre e produzirem raios X. Não relativisticamente, qual seria a velocidade máxima desses elétrons?
26. Um núcleo de hélio nu tem duas cargas positivas e uma massa de\(6.64\times 10^{-27}\: \mathrm{kg}\)
(a) Calcule sua energia cinética em joules a 2,00% da velocidade da luz.
(b) O que é isso em elétron-volts?
(c) Qual voltagem seria necessária para obter essa energia?
27. Conceitos integrados
Íons gasosos de carga única são acelerados do repouso por meio de uma voltagem de 13,0 V. A que temperatura a energia cinética média das moléculas de gás será a mesma que a dada a esses íons?
Solução
\(1.00\times 10^{5}\: \mathrm{K}\)
28. Conceitos integrados
Acredita-se que a temperatura próxima ao centro do Sol seja de 15 milhões de graus Celsius (\(1.5\times{10^{7}}^{\circ}C\)). Através de qual voltagem um íon carregado individualmente deve ser acelerado para ter a mesma energia que a energia cinética média dos íons nessa temperatura?
29. Conceitos integrados
(a) Qual é a potência média de um desfibrilador cardíaco que dissipa 400 J de energia em 10,0 ms?
(b) Considerando a saída de alta potência, por que o desfibrilador não produz queimaduras graves?
Solução
(a)\(4\times 10^{4}\: \mathrm{W}\)
(b) Um desfibrilador não causa queimaduras graves porque a pele conduz bem a eletricidade em altas tensões, como as usadas nos desfibriladores. O gel usado ajuda na transferência de energia para o corpo, e a pele não absorve a energia, mas a deixa passar para o coração.
30. Conceitos integrados
Um raio atinge uma árvore, movendo 20,0 C de carga através de uma diferença de potencial de\(1.00\times 10^{2}\: \mathrm{MV}\). (a) Que energia foi dissipada? (b) Que massa de água poderia ser elevada\(15^{\circ}C\) até o ponto de ebulição e depois fervida com essa energia? (c) Discuta os danos que podem ser causados à árvore pela expansão do vapor fervente.
31. Conceitos integrados
Um aquecedor de biberões de 12,0 V operado por bateria aquece 50,0 g de vidro,\(2.50\times 10^{2}\: \mathrm{g}\) de fórmula para bebês e\(2.00\times 10^{2}\: \mathrm{g}\) de alumínio de\(20.0^{\circ}C\) para\(90.0^{\circ}C\).
(a) Quanta carga é movida pela bateria?
(b) Quantos elétrons por segundo fluem se levar 5,00 min para aquecer a fórmula? (Dica: suponha que o calor específico da fórmula para bebês seja aproximadamente o mesmo que o calor específico da água.)
Solução
(a)\(7.40\times 10^{3}\: \mathrm{C}\)
(b)\(1.54\times 10^{20}\: \mathrm{electrons\: per\: second}\)
32. Conceitos integrados
Um carro operado por bateria utiliza um sistema de 12,0 V. Encontre a carga que as baterias devem ser capazes de mover para acelerar o carro de 750 kg do repouso para 25,0 m/s, fazê-lo subir uma colina\(2.00\times 10^{2}\: \mathrm{m}\) alta e, em seguida, fazer com que ele viaje a 25,0 m/s constantes exercendo uma\(5.00\times 10^{2}\: \mathrm{N}\) força por uma hora.
Solução
\(3.89\times 10^{6}\: \mathrm{C}\)
33. Conceitos integrados
A probabilidade de fusão aumenta consideravelmente quando os núcleos apropriados são unidos, mas a repulsão mútua de Coulomb deve ser superada. Isso pode ser feito usando a energia cinética de íons gasosos de alta temperatura ou acelerando os núcleos um em direção ao outro. (a) Calcule a energia potencial de dois núcleos carregados individualmente separados\(1.00\times 10^{-12}\: \mathrm{m}\) por encontrando a voltagem de um a essa distância e multiplicando pela carga do outro. (b) A que temperatura os átomos de um gás terão uma energia cinética média igual a essa energia potencial elétrica necessária?
34. Resultados irracionais
(a) Encontre a tensão próxima a uma esfera metálica de 10,0 cm de diâmetro que tenha 8,00 C de excesso de carga positiva nela.
(b) O que não é razoável nesse resultado?
(c) Quais suposições são responsáveis?
Solução
(a)\(1.44\times 10^{12}\: \mathrm{V}\)
(b) Essa tensão é muito alta. Uma esfera de 10,0 cm de diâmetro nunca poderia manter essa tensão; ela descarregaria.
(c) Uma carga de 8,00 C é mais carga do que pode ser razoavelmente acumulada em uma esfera desse tamanho.
35. Construa seu próprio problema
Considere uma bateria usada para fornecer energia a um telefone celular. Crie um problema no qual você determine a energia que deve ser fornecida pela bateria e, em seguida, calcule a quantidade de carga que ela deve ser capaz de mover para fornecer essa energia. Entre as coisas a serem consideradas estão as necessidades de energia e a voltagem da bateria. Talvez seja necessário interpretar as classificações da bateria do fabricante em amperes-hora como energia em joules.
19.2: Potencial elétrico em um campo elétrico uniforme
36. Mostre que as unidades de V/m e N/C para intensidade do campo elétrico são de fato equivalentes.
37. Qual é a intensidade do campo elétrico entre duas placas condutoras paralelas separadas por 1,00 cm e com uma diferença de potencial (tensão) entre elas\(1.50\times 10^{4}\: \mathrm{V}\)?
38. A intensidade do campo elétrico entre duas placas condutoras paralelas separadas por 4,00 cm é\(7.50\times 10^{4}\: \mathrm{V/m}\).
(a) Qual é a diferença de potencial entre as placas?
(b) Considera-se que a placa com o menor potencial está em zero volts. Qual é o potencial de 1,00 cm dessa placa (e 3,00 cm da outra)?
Solução
(a)\(3.00\: \mathrm{kV}\)
(b)\(750\: \mathrm{V}\)
39. A que distância estão duas placas condutoras que têm uma intensidade de campo elétrico\(4.50\times 10^{3}\: \mathrm{V/m}\) entre elas, se a diferença de potencial for de 15,0 kV?
40. (a) A intensidade do campo elétrico entre duas placas condutoras paralelas excederá a força de ruptura do ar (\(3.0\times 10^{6}\: \mathrm{V/m}\)) se as placas forem separadas por 2,00 mm e uma diferença de potencial\(5.0\times 10^{3}\: \mathrm{V}\) for aplicada?
(b) Quão próximas as placas podem estar com essa tensão aplicada?
Solução
(a) Não. A intensidade do campo elétrico entre as placas é menor do\(2.5\times 10^{6}\: \mathrm{V/m}\) que a força de ruptura do ar (\(3.0\times 10^{6}\: \mathrm{V/m}\)).
(b)\(1.7\: \mathrm{mm}\)
41. A voltagem através de uma membrana que forma uma parede celular é de 80,0 mV e a membrana tem 9,00 nm de espessura. Qual é a intensidade do campo elétrico? (O valor é surpreendentemente grande, mas correto. As membranas são discutidas em Capacitores e Dielétricos e Condução Nervosa—Eletrocardiogramas.) Você pode assumir um campo elétrico uniforme.
42. As paredes das membranas das células vivas têm campos elétricos surpreendentemente grandes através delas devido à separação de íons. (As membranas são discutidas com alguns detalhes em Condução Nervosa—Eletrocardiogramas.) Qual é a voltagem em uma membrana de 8,00 nm de espessura se a intensidade do campo elétrico nela for de 5,50 mV/m? Você pode assumir um campo elétrico uniforme.
Solução
\(44.0\: \mathrm{mV}\)
43. Duas placas condutoras paralelas são separadas por 10,0 cm e uma delas é considerada a zero volts.
(a) Qual é a intensidade do campo elétrico entre eles, se o potencial de 8,00 cm da placa de zero volt (e 2,00 cm da outra) for 450 V?
(b) Qual é a tensão entre as placas?
44. Encontre a diferença máxima de potencial entre duas placas condutoras paralelas separadas por 0,500 cm de ar, dada a intensidade máxima sustentável do campo elétrico existente no ar\(3.0\times 10^{6}\: \mathrm{V/m}\).
Solução
\(15\: \mathrm{kV}\)
45. Um íon de carga dupla é acelerado para uma energia de 32,0 keV pelo campo elétrico entre duas placas condutoras paralelas separadas por 2,00 cm. Qual é a intensidade do campo elétrico entre as placas?
46. Um elétron deve ser acelerado em um campo elétrico uniforme com uma intensidade de\(2.00\times 10^{6}\: \mathrm{V/m}\).
(a) Qual energia em keV é dada ao elétron se ele for acelerado em 0,400 m?
(b) Em que distância ele teria que ser acelerado para aumentar sua energia em 50,0 GeV?
Solução
(a)\(800\: \mathrm{KeV}\)
(b)\(25.0\: \mathrm{km}\)
19.3: Potencial elétrico devido a uma carga pontual
47. Uma esfera de plástico de 0,500 cm de diâmetro, usada em uma demonstração de eletricidade estática, tem uma carga de 40,0 pC uniformemente distribuída em sua superfície. Qual é o potencial próximo à sua superfície?
Solução
\(144\: \mathrm{V}\)
48. Qual é o potencial\(0.530\times 10^{-10}\: \mathrm{m}\) de um próton (a distância média entre o próton e o elétron em um átomo de hidrogênio)?
49. (a) Uma esfera tem uma superfície uniformemente carregada com 1,00 C. A que distância de seu centro está o potencial de 5,00 MV?
(b) O que sua resposta implica sobre o aspecto prático de isolar uma carga tão grande?
Solução
(a) 1,80 km
(b) Uma carga de 1 C é uma quantidade muito grande de carga; uma esfera de raio de 1,80 km não é prática.
50. A que distância de uma carga\(1.00\: \mu \mathrm{C}\) pontual o potencial será de 100 V? A que distância estará\(2.00\times 10^{2}\: \mathrm{V}\)?
51. Quais são o sinal e a magnitude de uma carga pontual que produz um potencial\(-2.00\: \mathrm{V}\) a uma distância de 1,00 mm?
Solução
\(-2.22\times 10^{-13}\: \mathrm{C}\)
52. Se o potencial devido a uma carga pontual estiver\(5.00\times 10^{2}\: \mathrm{V}\) a uma distância de 15,0 m, quais são o sinal e a magnitude da carga?
53. Na fissão nuclear, um núcleo se divide aproximadamente ao meio.
(a) Qual é o potencial\(2.00\times 10^{-14}\: \mathrm{m}\) de um fragmento que contém 46 prótons?
(b) Qual é a energia potencial em MeV de um fragmento com carga semelhante a essa distância?
Solução
(a)\(3.31\times 10^{6}\: \mathrm{V}\)
(b)\(152\: \mathrm{MeV}\)
54. Um gerador Van de Graaff de pesquisa tem uma esfera metálica de 2,00 m de diâmetro com uma carga de 5,00 mC nela.
(a) Qual é o potencial próximo à sua superfície?
(b) A que distância de seu centro está o potencial de 1,00 MV?
(c) Um átomo de oxigênio com três elétrons ausentes é liberado perto do gerador Van de Graaff. Qual é sua energia em MeV a essa distância?
55. Um pulverizador de tinta eletrostática tem uma esfera metálica de 0,200 m de diâmetro com um potencial de 25,0 kV que repele gotículas de tinta em um objeto aterrado.
(a) Qual carga está na esfera?
(b) Qual carga uma gota de tinta de 0,100 mg deve ter para chegar ao objeto com uma velocidade de 10,0 m/s?
Solução
(a)\(2.78\times10^{-7}\: \mathrm{C}\)
(b)\(2.00\times 10^{-10}\: \mathrm{C}\)
56. Em um dos experimentos clássicos de física nuclear do início do século XX, uma partícula alfa foi acelerada em direção a um núcleo dourado e seu caminho foi substancialmente desviado pela interação de Coulomb. Se a energia do núcleo alfa de dupla carga fosse de 5,00 MeV, quão perto do núcleo dourado (79 prótons) ele poderia chegar antes de ser desviado?
57. (a) Qual é o potencial entre dois pontos situados a 10 cm e 20 cm de uma carga\(3.0\: \mu \mathrm{C}\) pontual?
(b) Para qual local o ponto de 20 cm deve ser movido para aumentar essa diferença de potencial em um fator de dois?
58. Resultados irracionais
(a) Qual é a velocidade final de um elétron acelerado do repouso por meio de uma tensão de 25,0 MV por um terminal Van de Graaff com carga negativa?
(b) O que não é razoável nesse resultado?
(c) Quais suposições são responsáveis?
Solução
(a)\(2.96\times 10^{9}\: \mathrm{m/s}\)
(b) Essa velocidade é muito grande. É mais rápido do que a velocidade da luz.
(c) A suposição de que a velocidade do elétron é muito menor que a da luz e que o problema não requer um tratamento relativístico produz uma resposta maior que a velocidade da luz.
19.4: Linhas equipotenciais
59. (a) Desenhe as linhas equipotenciais próximas a uma carga pontual +\(q\). Indique a direção do aumento do potencial.
(b) Faça o mesmo com uma cobrança de pontos\(-3q\).
60. Esboce as linhas equipotenciais para as duas cargas positivas iguais mostradas na Figura 19.5.6. Indique a direção do aumento do potencial.
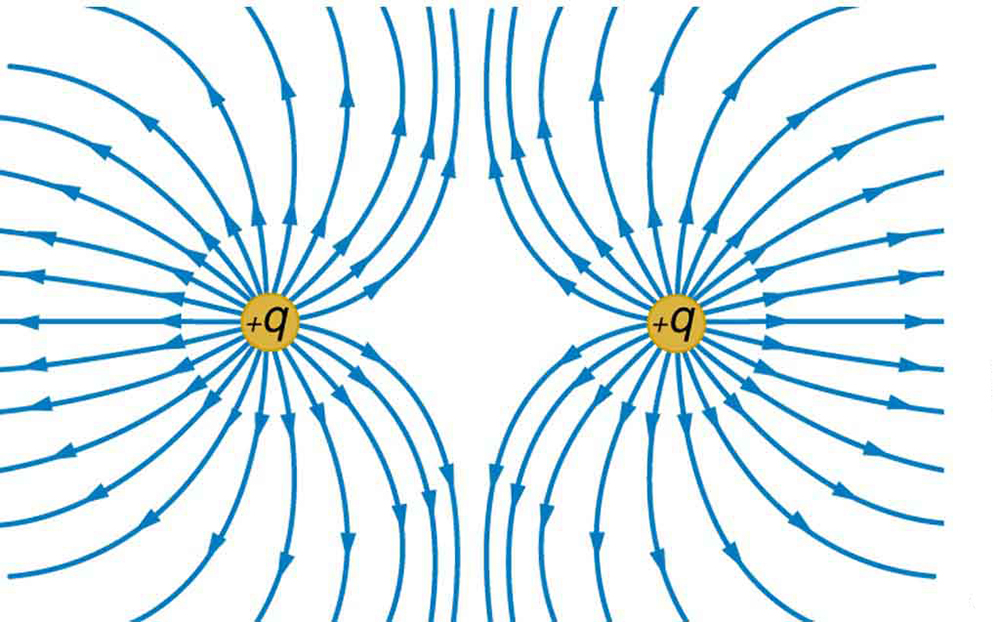
Figura 19.5.6: O campo elétrico próximo a duas cargas positivas iguais é direcionado para longe de cada uma das cargas.
61. A Figura 19.5.7 mostra as linhas do campo elétrico próximas a duas cargas\(q_{1}\) e\(q_{2}\), a primeira com uma magnitude quatro vezes maior que a segunda. Esboce as linhas equipotenciais para essas duas cargas e indique a direção do aumento do potencial.
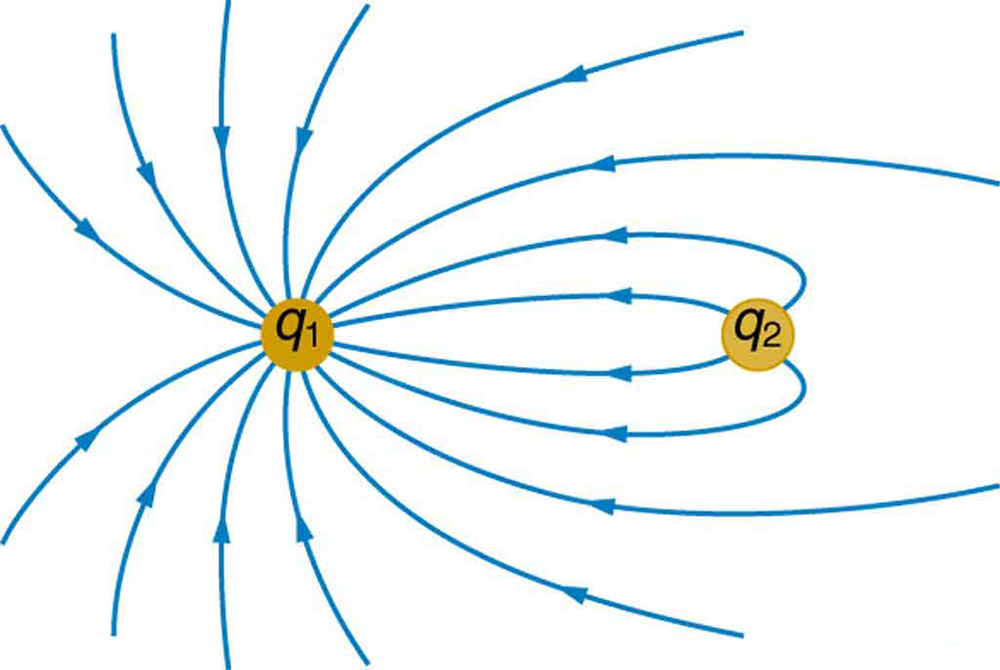
O campo elétrico perto de duas cargas.
62. Desenhe as linhas equipotenciais a uma longa distância das cargas mostradas na Figura 19.5.7. Indique a direção do aumento do potencial.
63. Desenhe as linhas equipotenciais nas proximidades de duas cargas opostas, onde a carga negativa é três vezes maior em magnitude que a positiva. Consulte a Figura 19.5.7 para uma situação semelhante. Indique a direção do aumento do potencial.
64. Esboce as linhas equipotenciais nas proximidades do condutor carregado negativamente na Figura 19.5.8. Como esses equipotenciais parecerão a uma longa distância do objeto?

Figura 19.5.8: Um condutor carregado negativamente.
65. Desenhe as linhas equipotenciais ao redor das duas placas condutoras mostradas na Figura 19.5.9, considerando que a placa superior é positiva e a placa inferior tem uma quantidade igual de carga negativa. Certifique-se de indicar a distribuição da carga nas placas. O campo é mais forte onde as placas estão mais próximas? Por que deveria ser?
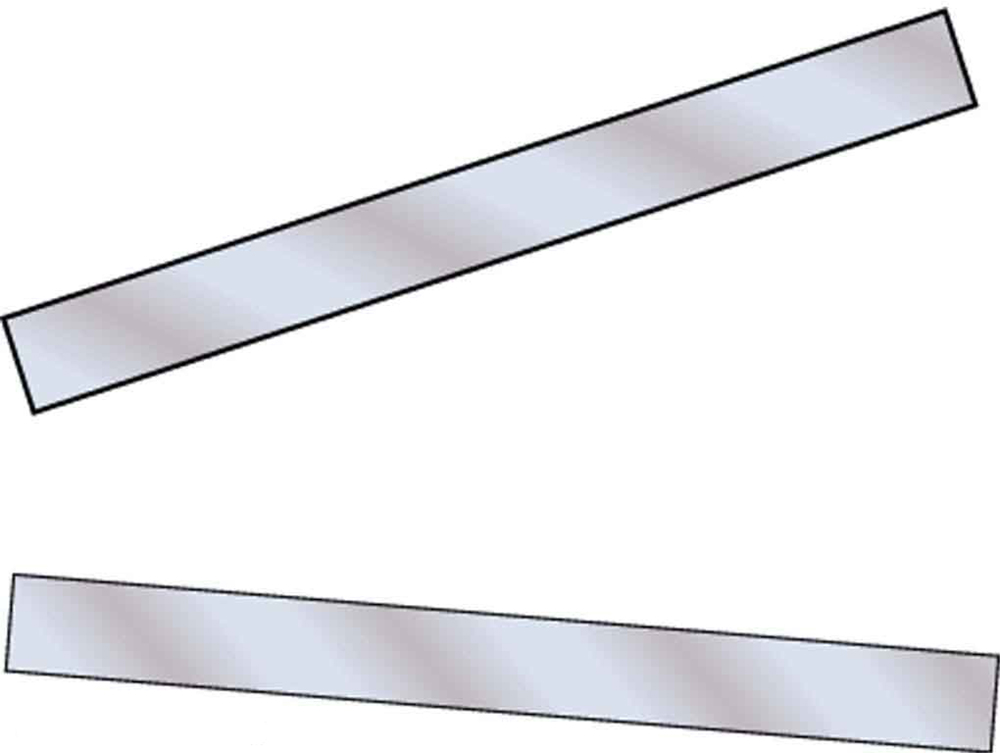
Figura 19.5.9
66. (a) Esboce as linhas do campo elétrico nas proximidades do isolador carregado na Figura 19.5.10. Observe sua distribuição de carga não uniforme. (b) Desenhe linhas equipotenciais ao redor do isolador. Indique a direção do aumento do potencial.
Figura 19.5.10: Uma haste isolante carregada, como a que poderia ser usada em uma demonstração em sala de aula.
67. A cobrança natural no solo em um bom dia em campo aberto é\(-1.00\: \mathrm{nC/m^{2}}\).
(a) Qual é o campo elétrico em relação ao solo a uma altura de 3,00 m?
(b) Calcule o potencial elétrico nessa altura.
(c) Esboce campo elétrico e linhas equipotenciais para este cenário.
68. O raio elétrico menor (Narcine bancroftii) mantém uma carga incrível em sua cabeça e uma carga igual em magnitude, mas oposta em sinal na cauda (Figura).
(a) Desenhe as linhas equipotenciais ao redor do raio.
(b) Esboce os equipotenciais quando o raio estiver próximo de um navio com uma superfície condutora.
(c) Como essa distribuição de carga poderia ser útil para o raio?

Figura 19.5.11: Raio elétrico menor (Narcine bancroftii) (crédito: Administração Nacional Oceânica e Atmosférica, Coleção de Pesca da NOAA).
19.5: Capacitores e dielétricos
69. Qual carga é armazenada em um\(180\: \mu \mathrm{F}\) capacitor quando 120 V são aplicados a ele?
Solução
\(21.6\: \mathrm{mC}\)
70. Encontre a carga armazenada quando 5,50 V é aplicado a um capacitor de 8,00 pF.
71. Qual carga é armazenada no capacitor no Example?
Solução
\(80.0\: \mathrm{mC}\)
72. Calcule a tensão aplicada a um\(2.00\: \mu \mathrm{F}\) capacitor quando ele mantém\(3.10\: \mu \mathrm{C}\) a carga.
73. Qual voltagem deve ser aplicada a um capacitor de 8,00 nF para armazenar 0,160 mC de carga?
Solução
20,0 kV
74. Qual capacitância é necessária para armazenar\(3.00\: \mu \mathrm{C}\) a carga a uma tensão de 120 V?
75. Qual é a capacitância do terminal de um grande gerador Van de Graaff, já que ele armazena 8,00 mC de carga a uma voltagem de 12,0 MV?
Solução
\(667\: \mathrm{pF}\)
76. Encontre a capacitância de um capacitor de placa paralela com placas de área\(5.00\: \mathrm{m^{2}}\) separadas por 0,100 mm de Teflon.
77. (a) Qual é a capacitância de um capacitor de placa paralela com placas de área\(1.50\: \mathrm{m^{2}}\) separadas por 0,0200 mm de borracha de neoprene?
(b) Que carga ele retém quando 9,00 V é aplicado a ele?
Solução
(a)\(4.4\: \mu \mathrm{F}\)
(b)\(4.0\times 10^{-5}\: \mathrm{C}\)
78. Conceitos integrados
Um brincalhão aplica 450 V a um\(80.0\: \mu \mathrm{F}\) capacitor e depois o joga para uma vítima inocente. O dedo da vítima é queimado pela descarga do capacitor através de 0.200 g de carne. Qual é o aumento da temperatura da carne? É razoável presumir que não há mudança de fase?
79. Resultados irracionais
(a) Um determinado capacitor de placa paralela tem placas de área\(4.00\: \mathrm{m^{2}}\), separadas por 0,0100 mm de náilon, e armazena 0,170 C de carga. Qual é a voltagem aplicada?
(b) O que não é razoável nesse resultado?
(c) Quais suposições são responsáveis ou inconsistentes?
Solução
(a) 14,2 kV
(b) A tensão é excessivamente grande, mais de 100 vezes a tensão de ruptura do náilon.
(c) A carga assumida é excessivamente grande e não pode ser armazenada em um capacitor dessas dimensões.
19.6: Capacitores em série e paralelos
80. Encontre a capacitância total da combinação de capacitores na Figura 19.7.4.
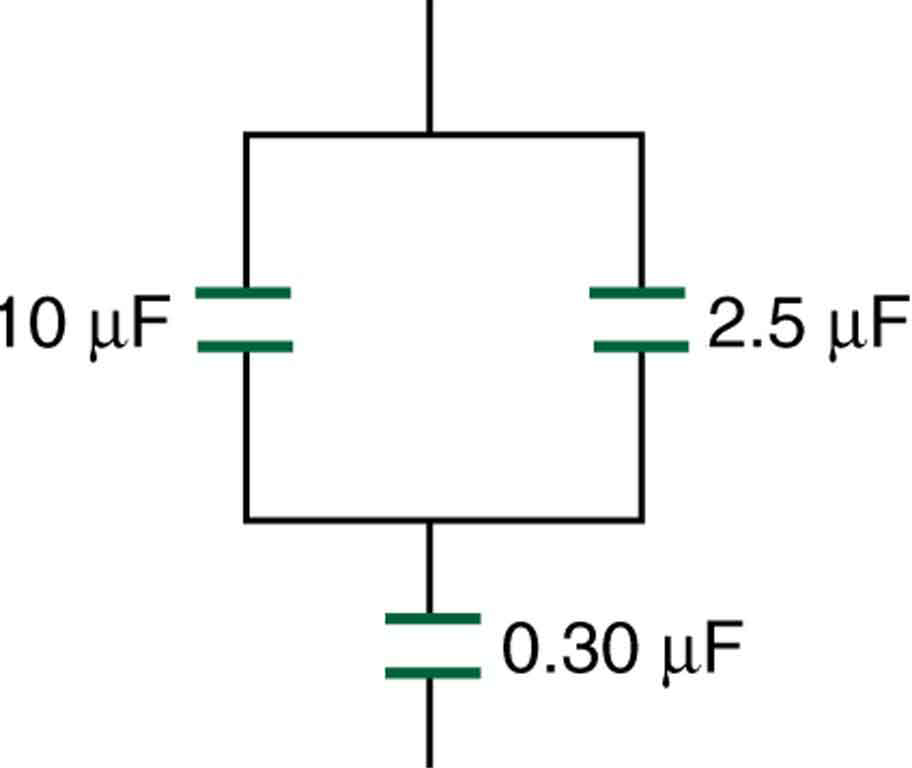
Figura 19.7.4: Uma combinação de conexões em série e paralelas de capacitores.
Solução
\(0.293\: \mu \mathrm{F}\)
81. Suponha que você queira um banco de capacitores com uma capacitância total de 0,750 F e possua vários capacitores de 1,50 mF. Qual é o menor número que você poderia conectar para atingir seu objetivo e como você os conectaria?
82. Quais capacitâncias totais você pode criar conectando um\(8.00\: \mu \mathrm{F}\) capacitor\(5.00\: \mu \mathrm{F}\) e um?
Solução
\(3.08\: \mu \mathrm{F}\) em combinação em série,\(13.0\: \mu \mathrm{F}\) em combinação paralela
83. Encontre a capacitância total da combinação de capacitores mostrada na Figura 19.7.5.
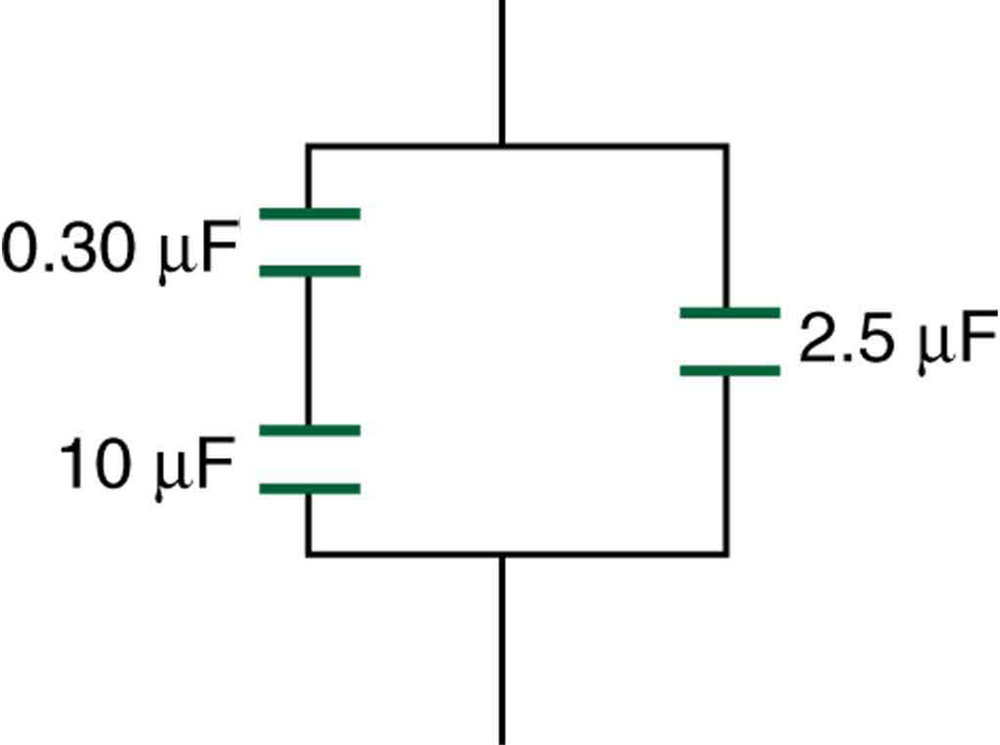
Figura 19.7.5: Uma combinação de conexões em série e paralelas de capacitores.
Solução
\(2.79\: \mu \mathrm{F}\)
84. Encontre a capacitância total da combinação de capacitores mostrada na Figura.
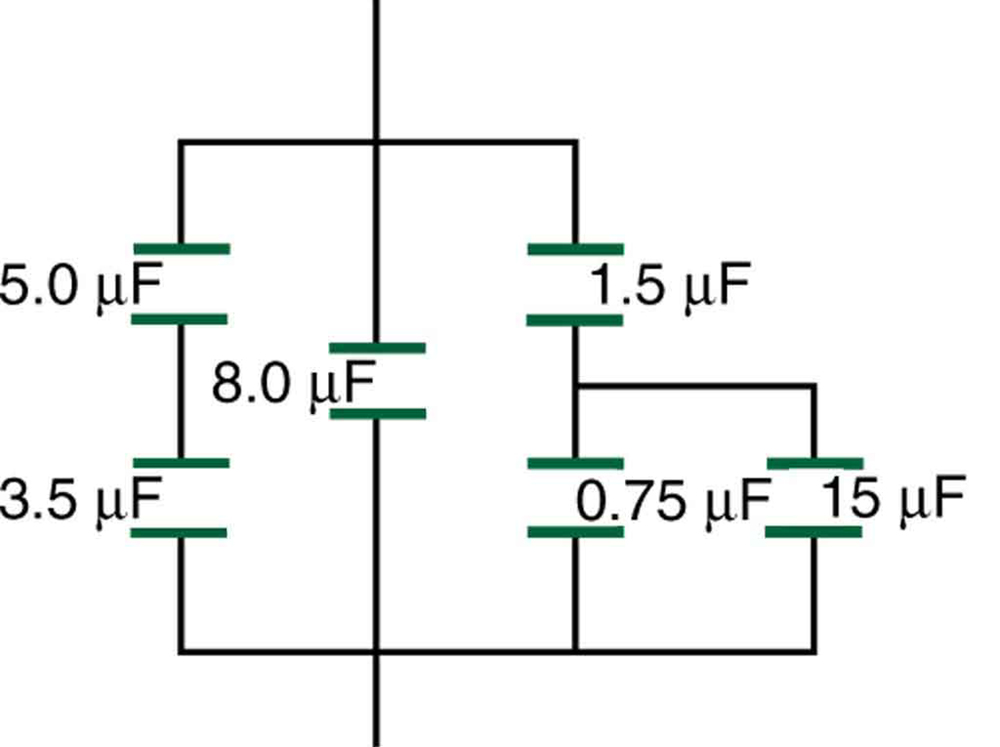
Figura 19.7.6: Uma combinação de conexões em série e paralelas de capacitores.
85. (a) Um\(8.00\: \mu \mathrm{F}\) capacitor é conectado em paralelo a outro capacitor, produzindo uma capacitância total de\(5.00\: \mu \mathrm{F}\). Qual é a capacitância do segundo capacitor?
(b) O que não é razoável nesse resultado?
(c) Quais suposições são irracionais ou inconsistentes?
Solução
(a)\(-3.00\: \mu \mathrm{F}\)
(b) Você não pode ter um valor negativo de capacitância.
(c) A suposição de que os capacitores estavam conectados em paralelo, e não em série, estava incorreta. Uma conexão paralela sempre produz uma capacitância maior, enquanto aqui uma capacitância menor foi assumida. Isso só pode acontecer se os capacitores estiverem conectados em série.
19.7: Energia armazenada em capacitores
86. (a) Para que é carregada a energia armazenada no\(10.0\: \mu \mathrm{F}\) capacitor de um desfibrilador cardíaco\(9.00\times 10^{3}\: \mathrm{V}\)?
(b) Encontre o valor da cobrança armazenada.
Solução
(a)\(405\: \mathrm{J}\)
(b)\(90.0\: \mathrm{mC}\)
87. Na cirurgia cardíaca aberta, uma quantidade muito menor de energia desfibrilará o coração.
(a) Qual voltagem é aplicada ao\(8.00\: \mu \mathrm{F}\) capacitor de um desfibrilador cardíaco que armazena 40,0 J de energia?
(b) Encontre o valor da cobrança armazenada.
Solução
(a) 3,16 kV
(b) 25,3 mC
88. Um\(165\: \mu \mathrm{F}\) capacitor é usado em conjunto com um motor. Quanta energia é armazenada nela quando 119 V é aplicado?
89. Suponha que você tenha uma bateria de 9,00 V, um\(2.00\: \mu \mathrm{F}\) capacitor e um\(7.40\: \mu \mathrm{F}\) capacitor.
(a) Encontre a carga e a energia armazenadas se os capacitores estiverem conectados à bateria em série.
(b) Faça o mesmo para uma conexão paralela.
Solução
(a)\(1.42\times 10^{-5}\: \mathrm{C},\: 6.38\times 10^{-5}\: \mathrm{J}\)
(b)\(8.46\times 10^{-5}\: \mathrm{C},\: 3.81\times 10^{-4}\: \mathrm{J}\)
90. Um físico nervoso teme que as duas prateleiras de metal de sua estante com estrutura de madeira possam obter uma alta voltagem se carregadas por eletricidade estática, talvez produzida por fricção.
(a) Qual é a capacitância das prateleiras vazias se elas tiverem área\(1.00\times 10^{2}\: \mathrm{m^{2}}\) e estiverem separadas por 0,200 m?
(b) Qual é a tensão entre eles se cargas opostas de magnitude 2,00 nC forem colocadas sobre eles?
(c) Para mostrar que essa tensão representa um pequeno risco, calcule a energia armazenada.
Solução
(a)\(4.43\times 10^{-12}\: \mathrm{F}\)
(b)\(452\: \mathrm{V}\)
(c)\(4.52\times 10^{-7}\: \mathrm{J}\)
91. Mostre que, para um determinado material dielétrico, a energia máxima que um capacitor de placa paralela pode armazenar é diretamente proporcional ao volume de dielétrico (\(\mathrm{Volume}\: =A\cdot d\)). Observe que a tensão aplicada é limitada pela rigidez dielétrica.
92. Construa seu próprio problema
Considere um desfibrilador cardíaco semelhante ao discutido no Exemplo. Crie um problema no qual você examine a carga armazenada no capacitor de um desfibrilador em função da energia armazenada. Entre as coisas a serem consideradas estão a tensão aplicada e se ela deve variar com a energia a ser fornecida, a faixa de energias envolvidas e a capacitância do desfibrilador. Você também pode considerar a energia muito menor necessária para a desfibrilação durante uma cirurgia cardíaca aberta como uma variação desse problema.
93. (a) Em um determinado dia, é preciso\(9.60\times 10^{3}\: \mathrm{J}\) energia elétrica para dar partida no motor de um caminhão. Calcule a capacitância de um capacitor que possa armazenar essa quantidade de energia a 12,0 V.
(b) O que não é razoável nesse resultado?
(c) Quais suposições são responsáveis?
Solução
(a)\(133\: \mathrm{F}\)
(b) Esse capacitor seria muito grande para ser carregado com um caminhão. O tamanho do capacitor seria enorme.
(c) Não é razoável supor que um capacitor possa armazenar a quantidade de energia necessária.


