17.7: Ultrassom
- Page ID
- 194207
Objetivos de
Ao final desta seção, você poderá:
- Defina a impedância acústica e o coeficiente de reflexão da intensidade.
- Descreva os usos médicos e outros da tecnologia de ultrassom.
- Calcule a impedância acústica usando valores de densidade e a velocidade do ultrassom.
- Calcule a velocidade de um objeto em movimento usando o ultrassom com deslocamento Doppler.
Qualquer som com uma frequência acima de 20.000 Hz (ou 20 kHz), ou seja, acima da frequência audível mais alta, é definido como ultrassom. Na prática, é possível criar frequências de ultrassom de até mais de um gigahertz. (Frequências mais altas são difíceis de criar; além disso, elas se propagam mal porque são muito fortemente absorvidas.) O ultrassom tem um grande número de aplicações, que vão desde alarmes contra roubo até o uso na limpeza de objetos delicados até os sistemas de orientação de morcegos. Começamos nossa discussão sobre o ultrassom com algumas de suas aplicações na medicina, nas quais ele é amplamente utilizado tanto para diagnóstico quanto para terapia.
Características do ultrassom
Qualquer som com uma frequência acima de 20.000 Hz (ou 20 kHz), ou seja, acima da frequência audível mais alta, é definido como ultrassom. Na prática, é possível criar frequências de ultrassom de até mais de um gigahertz. (Frequências mais altas são difíceis de criar; além disso, elas se propagam mal porque são muito fortemente absorvidas.) O ultrassom tem um grande número de aplicações, que vão desde alarmes contra roubo até o uso na limpeza de objetos delicados até os sistemas de orientação de morcegos. Começamos nossa discussão sobre o ultrassom com algumas de suas aplicações na medicina, nas quais ele é amplamente utilizado tanto para diagnóstico quanto para terapia.
Ultra-som em terapia médica
O ultrassom, como qualquer onda, carrega energia que pode ser absorvida pelo meio que a carrega, produzindo efeitos que variam com a intensidade. Quando focado nas intensidades do\(10^3\)\(10^5 \, W/m^2\) ultrassom, o ultrassom pode ser usado para quebrar cálculos biliares ou pulverizar tecido canceroso em procedimentos cirúrgicos (Figura\(\PageIndex{2}\)). Intensidades tão grandes podem danificar células individuais, fazendo com que seu protoplasma flua para dentro delas, alterando sua permeabilidade ou rompendo suas paredes por meio de cavitação. A cavitação é a criação de cavidades de vapor em um fluido - as vibrações longitudinais no ultrassom comprimem e expandem alternativamente o meio e, em amplitudes suficientes, a expansão separa as moléculas. A maioria dos danos causados pela cavitação ocorre quando as cavidades colapsam, produzindo pressões de choque ainda maiores.
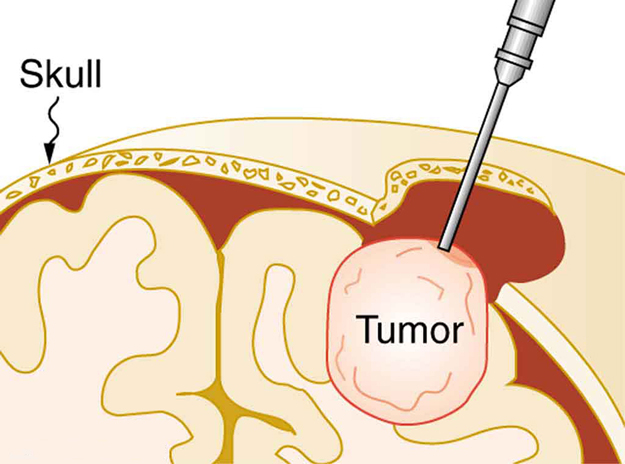
A maior parte da energia transportada pelo ultrassom de alta intensidade no tecido é convertida em energia térmica. De fato, intensidades de\(10^3\) to\(10^4 \, W/m^2\) são comumente usadas para tratamentos de calor profundo chamados de diatermia por ultrassom. Frequências de 0,8 a 1 MHz são típicas. Tanto no atletismo quanto na fisioterapia, a diatermia ultrassônica é mais frequentemente aplicada em músculos lesionados ou sobrecarregados para aliviar a dor e melhorar a flexibilidade. O terapeuta precisa de habilidade para evitar “queimaduras ósseas” e outros danos nos tecidos causados pelo superaquecimento e cavitação, às vezes agravados pela reflexão e focalização do ultrassom pelo tecido articular e ósseo.
Em alguns casos, você pode encontrar uma escala de decibéis diferente, chamada nível de pressão sonora, quando o ultrassom viaja na água ou em tecidos humanos e outros tecidos biológicos. Não usaremos a escala aqui, mas é notável que os números dos níveis de pressão sonora variam de 60 a 70 dB mais do que você citaria\(β\), o nível de intensidade sonora usado neste texto. Se você encontrar um nível de pressão sonora de 220 decibéis, então, não é uma intensidade astronomicamente alta, mas equivalente a cerca de 155 dB — alta o suficiente para destruir tecidos, mas não tão excessivamente alta quanto parece à primeira vista.
Ultrassom em diagnósticos médicos
Quando usadas para geração de imagens, ondas ultrassônicas são emitidas por um transdutor, um cristal exibindo o efeito piezoelétrico (a expansão e contração de uma substância quando uma voltagem é aplicada sobre ela, causando uma vibração do cristal). Essas vibrações de alta frequência são transmitidas para qualquer tecido em contato com o transdutor. Da mesma forma, se uma pressão for aplicada ao cristal (na forma de uma onda refletida nas camadas de tecido), é produzida uma voltagem que pode ser registrada. Portanto, o cristal atua como transmissor e receptor de som. O ultrassom também é parcialmente absorvido pelo tecido em seu caminho, tanto na viagem para longe do transdutor quanto na jornada de retorno. A partir do momento em que o sinal original é enviado e quando as reflexões de vários limites entre as mídias são recebidas (bem como uma medida da perda de intensidade do sinal), a natureza e a posição de cada limite entre tecidos e órgãos podem ser deduzidas.
Reflexões nos limites entre dois meios diferentes ocorrem devido a diferenças em uma característica conhecida como impedância acústica\(Z\) de cada substância. A impedância é definida como
\[Z = \rho v,\]
onde\(\rho\) é a densidade do meio (em kg/m^3\)) e\(v\) é a velocidade do som no meio (em m/s). As unidades para\(Z\) são, portanto,\(kg/(m^2 \cdot s)\).
A tabela\(\PageIndex{1}\) mostra a densidade e a velocidade do som através de várias mídias (incluindo vários tecidos moles) e as impedâncias acústicas associadas. Observe que as impedâncias acústicas dos tecidos moles não variam muito, mas há uma grande diferença entre a impedância acústica do tecido mole e do ar e também entre o tecido mole e o osso.
| Médio | Densidade\((kg/m^3)\) | Velocidade do ultrassom (m/s) | Impedância acústica\((kg/(m^2\cdot s))\) |
|---|---|---|---|
| Ar | \ (kg/m^3)\)” style="alinhamento vertical:médio; ">1,3 | 330 | \ ((kg/ (m^2\ cdot s))\)” style="alinhamento vertical: meio; ">429 |
| Água | \ (kg/m^3)\)” style="alinhamento vertical:médio; ">1000 | 1500 | \ ((kg/ (m^2\ cdot s))\)” style="alinhamento vertical: meio; ">\(1.5 \times 10^6\) |
| Sangue | \ ((kg/m^3)\)” style="alinhamento vertical:médio; ">1060 | 1570 | \ ((kg/ (m^2\ cdot s))\)” style="alinhamento vertical: meio; ">\(1.66 \times 10^6\) |
| Gordo | \ (kg/m^3)\)” style="alinhamento vertical:médio; ">925 | 1450 | \ ((kg/ (m^2\ cdot s))\)” style="alinhamento vertical:meio; ">1,34 (1000000) |
| Músculo (médio) | \ ((kg/m^3)\)” style="alinhamento vertical:médio; ">1075 | 1590 | \ ((kg/ (m^2\ cdot s))\)” style="alinhamento vertical: meio; ">1,7 (1000000) |
| Osso (varia) | \ ((kg/m^3)\)” style="alinhamento vertical:médio; ">1400—1900 | 4080 | \ ((kg/ (m^2\ cdot s))\)” style="vertical-align:middle; ">5,7 a 7,8 (1000000) |
| Titanato de bário (material transdutor) | \ (kg/m^3)\)” style="alinhamento vertical:médio; ">5600 | 5500 | \ ((kg/ (m^2\ cdot s))\)” style="alinhamento vertical:meio; ">30,8 (1000000) |
No limite entre mídias de diferentes impedâncias acústicas, parte da energia da onda é refletida e outra é transmitida. Quanto maior a diferença na impedância acústica entre as duas mídias, maior a reflexão e menor a transmissão.
O coeficiente de reflexão de intensidade t\(a\) é definido como a razão entre a intensidade da onda refletida em relação à onda incidente (transmitida). Esta declaração pode ser escrita matematicamente como
\[a = \frac{\left(Z_{2} - Z_{1}\right)^2}{\left(Z_{1} + Z_{2}\right)^{2}},\]
onde\(Z_{1}\) e\(Z_{2}\) estão as impedâncias acústicas das duas mídias que compõem o limite. Um coeficiente de reflexão de zero (correspondente à transmissão total e nenhuma reflexão) ocorre quando as impedâncias acústicas dos dois meios são iguais. Uma “correspondência” de impedância (sem reflexão) fornece um acoplamento eficiente da energia sonora de um meio para outro. A imagem formada em um ultrassom é feita rastreando as reflexões (conforme mostrado na Figura\(\PageIndex{3}\)) e mapeando a intensidade das ondas sonoras refletidas em um plano bidimensional.
Exemplo\(\PageIndex{1}\): Calculate Acoustic Impedance and Intensity Reflection Coefficient: Ultrasound and Fat Tissue
(a) Usando os valores de densidade e velocidade do ultrassom fornecidos na Tabela\(\PageIndex{1}\), mostre que a impedância acústica do tecido adiposo é de fato\(1.34 \times 10^{6}kg / \left( m^{2} \cdot s \right)\).
(b) Calcule o coeficiente de reflexão da intensidade do ultrassom ao passar da gordura para o tecido muscular.
Estratégia para (a)
A impedância acústica pode ser calculada usando\(Z = \rho v\) e os valores de\(\rho\) e\(v\) encontrados na Tabela\(\PageIndex{1}\).
Solução para (a)
(1) Substitua os valores conhecidos da Tabela\(\PageIndex{1}\) em\(Z = \rho v\).
\[Z = \rho v = \left(925 kg/m^{3}\right)\left(1450 m/s\right)\]
(2) Calcule para encontrar a impedância acústica do tecido adiposo.
\[1.34 \times 10^{6} kg/\left(m^{2} \cdot s\right)\]
Esse valor é o mesmo que o valor dado para a impedância acústica do tecido adiposo.
O coeficiente de reflexão de intensidade para qualquer limite entre dois meios é dado por\(a = \frac{\left(Z_{2} - Z_{1}\right)^{2}}{\left(Z_{2} + Z_{1}\right)^{2}}\), e a impedância acústica do músculo é dada na Tabela\(\PageIndex{1}\).
Solução para (b)
Substitua os valores conhecidos em\(a = \frac{\left(Z_{2} - Z_{1}\right)^{2}}{\left(Z_{2} + Z_{1}\right)^{2}}\) para encontrar o coeficiente de reflexão da intensidade:
\[a = \frac{\left(Z_{2} - Z_{1}\right)^{2}}{\left(Z_{2} + Z_{1}\right)^{2}} = \frac{\left(1.34 \times 10^{6} kg/\left(m^{2} \cdot s\right) - 1.70 \times 10^{6} kg/\left(m^{2} \cdot s\right) \right)^{2}}{\left(1.70 \times 10^{6} kg / \left(m^{2}\cdot s\right) + 1.34 \times 10^{6} kg/ \left(m^{2} \cdot s \right) \right)^{2}} = 0.014\]
Discussão
Esse resultado significa que apenas 1,4% da intensidade do incidente é refletida, com o restante sendo transmitido.
As aplicações do ultrassom no diagnóstico médico produziram benefícios incontáveis sem riscos conhecidos. As intensidades de diagnóstico são muito baixas (aproximadamente\(10^{-2} W/m^{2}\)) para causar danos térmicos. Mais significativamente, o ultrassom está em uso há várias décadas e estudos de acompanhamento detalhados não mostram evidências de efeitos nocivos, muito diferente do caso das radiografias.
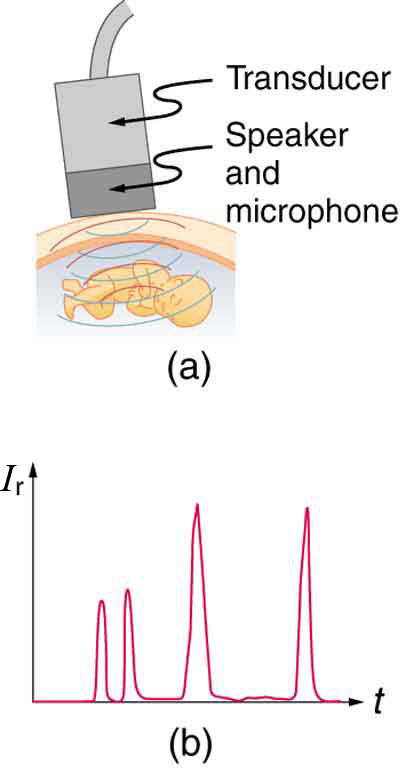
As aplicações de ultrassom mais comuns produzem uma imagem como a mostrada na Figura\(\PageIndex{4}\). O microfone do alto-falante emite um feixe direcional, varrendo o feixe pela área de interesse. Isso é feito com várias fontes de ultrassom na cabeça da sonda, que são escalonadas para interferir construtivamente em uma determinada direção ajustável. Os ecos são medidos em função da posição e da profundidade. Um computador constrói uma imagem que revela a forma e a densidade das estruturas internas.
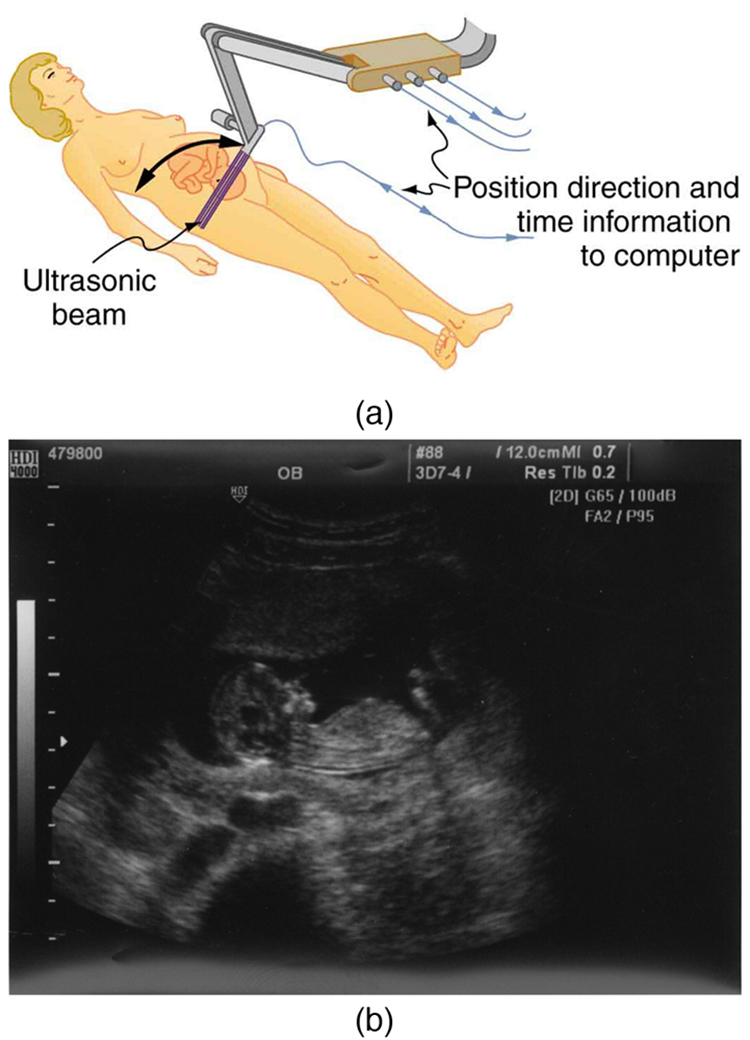
Quantos detalhes o ultrassom pode revelar? A imagem na Figura\(\PageIndex{4}\) é típica de sistemas de baixo custo, mas\(\PageIndex{5}\) mostra os detalhes notáveis possíveis com sistemas mais avançados, incluindo imagens 3D. O ultrassom hoje é comumente usado no cuidado pré-natal. Essa imagem pode ser usada para verificar se o feto está se desenvolvendo em uma taxa normal e ajudar na determinação de problemas graves no início da gravidez. O ultrassom também é amplamente utilizado para obter imagens das câmaras do coração e do fluxo de sangue dentro do coração batendo, usando o efeito Doppler (ecocardiologia).
Sempre que uma onda é usada como sonda, é muito difícil detectar detalhes menores que seu comprimento de onda\(\lambda\). De fato, a tecnologia atual não pode fazer isso bem. Os exames abdominais podem usar uma frequência de 7 MHz, e a velocidade do som no tecido é de cerca de 1540 m/s - então o limite do comprimento de onda para os detalhes seria\(\lambda = \frac{v_{w}}{f} = \frac{1540 m/s}{7 \times 10^{6} Hz} = 0.22mm\). Na prática, é possível obter detalhes de 1 mm, o que é suficiente para muitos propósitos. O ultrassom de alta frequência permitiria maiores detalhes, mas não penetra tão bem quanto as frequências mais baixas. A regra prática aceita é que você pode digitalizar com eficácia até uma profundidade de aproximadamente\(500 \lambda\) no tecido. Para 7 MHz, esse limite de penetração é de 0,11 m. Frequências mais altas podem ser empregadas em órgãos menores, como o olho, mas não são práticas para observar profundamente o corpo.\(500 \times 0.22 mm\)
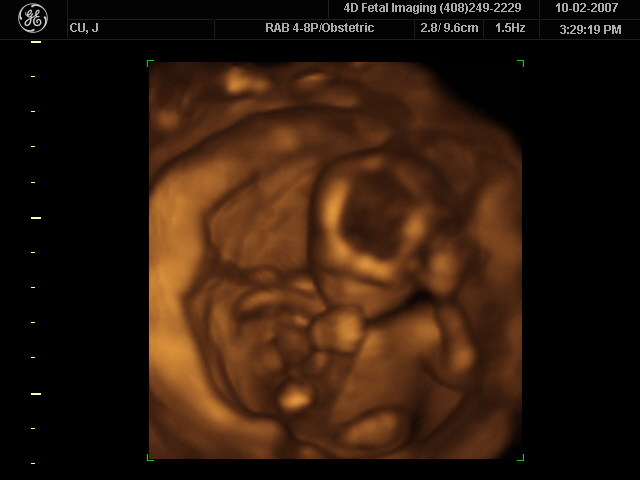
Além das informações de forma, os exames ultrassônicos podem produzir informações de densidade superiores às encontradas nos raios X, porque a intensidade de um som refletido está relacionada a mudanças na densidade. O som é refletido mais fortemente em locais onde as mudanças de densidade são maiores.
Outro grande uso do ultrassom no diagnóstico médico é detectar o movimento e determinar a velocidade por meio do desvio Doppler de um eco, conhecido como ultrassom com desvio Doppler. Essa técnica é usada para monitorar os batimentos cardíacos fetais, medir a velocidade do sangue e detectar oclusões nos vasos sanguíneos, por exemplo. (Veja a Figura\(\PageIndex{6}\).)
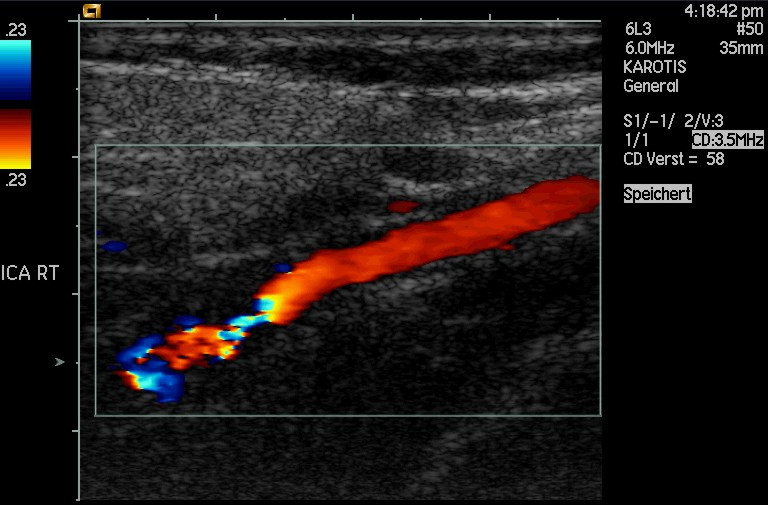
Uma técnica inteligente é usada para medir o desvio do Doppler em um eco. A frequência do som ecoado é sobreposta à frequência de transmissão, produzindo batidas. A frequência de batida é\(F_{B} = \vert f_{1} - f_{2} \vert \), e portanto, é diretamente proporcional ao desvio do Doppler (\(f_{1} - f_{2}\)) e, portanto, à velocidade do refletor. A vantagem dessa técnica é que o desvio do Doppler é pequeno (porque a velocidade do refletor é pequena), então seria necessária uma grande precisão para medir o deslocamento diretamente. Mas medir a frequência da batida é fácil e não é afetada se a frequência de transmissão variar um pouco. Além disso, a frequência de batida está na faixa audível e pode ser amplificada para feedback de áudio para o observador médico.
USOS DO RADAR DOPPLER SHIFTED
Os ecos de radar com desvio Doppler são usados para medir a velocidade do vento em tempestades, bem como as velocidades de aeronaves e automóveis. O princípio é o mesmo do ultrassom com desvio Doppler. Há evidências de que morcegos e golfinhos também podem sentir a velocidade de um objeto (como uma presa) refletindo seus sinais de ultrassom ao observar o desvio do Doppler.
Exemplo\(\PageIndex{2}\): Calculate Velocity of Blood: Doppler-Shifted Ultrasound
O ultrassom com frequência de 2,50 MHz é enviado para o sangue em uma artéria que está se movendo em direção à fonte a 20,0 cm/s, conforme ilustrado na Figura\(\PageIndex{7}\). Use a velocidade do som no tecido humano como 1540 m/s. (Suponha que a frequência de 2,50 MHz seja precisa de sete números significativos).
- Qual a frequência que o sangue recebe?
- Qual frequência retorna para a fonte?
- Qual frequência de batida é produzida se a fonte e as frequências de retorno forem misturadas?
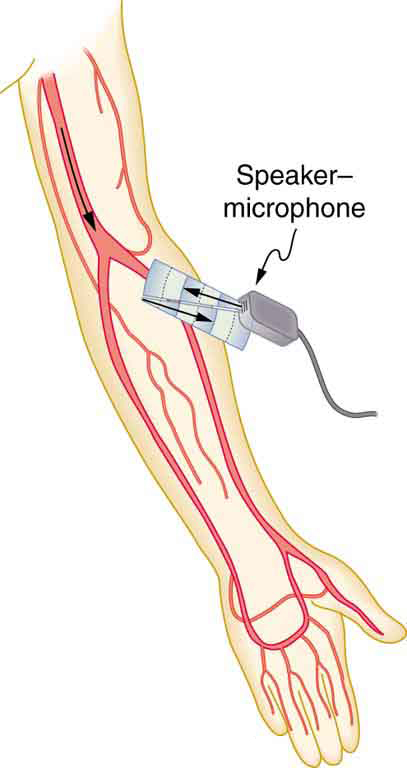
Estratégia
As duas primeiras perguntas podem ser respondidas usando\(f_{obs} = f_{s} \left(\frac{v_{w}}{v_{w} \pm v_{s}}\right)\) e\(f_{obs} = f_{s} \left(\frac{v_{w} \pm v_{obs}}{v_{w}}\right)\) para o deslocamento do Doppler. A última pergunta pergunta sobre a frequência da batida, que é a diferença entre as frequências original e de retorno.
Solução para (a)
- Identifique conhecidos:
- O sangue é um observador em movimento e, portanto, a frequência que ele recebe é dada por\[f_{obs} = f_{s} \left(\frac{v_{w} \pm v_{obs}}{v_{w}}\right)\].
- \(v_{b}\)é a velocidade do sangue (\(v_{obs}\)aqui) e o sinal de mais é escolhido porque o movimento é em direção à fonte.
- Insira os valores fornecidos na equação. \[f_{obs} = \left(2,500,000 Hz\right) \left( \frac{1540 m/s + 0.2 m/s}{1540 m/s}\right)\]
- Calcule para encontrar a frequência: 2.500.325 Hz.
Solução para (b)
- Identifique conhecidos:
- O sangue age como uma fonte móvel.
- O microfone atua como um observador estacionário.
- A frequência que sai do sangue é de 2.500.325 Hz, mas é deslocada para cima conforme dada por\[f_{obs} = f_{s} \left(\frac{v_{w}}{v_{w} - v_{b}}\right).\]
- \(f_{obs}\)é a frequência recebida pelo microfone do alto-falante.
- A velocidade da fonte é\(v_{b}\).
- O sinal de menos é usado porque o movimento é em direção ao observador.
- Insira os valores fornecidos na equação:\[f_{obs} = \left(2,500,325 Hz\right) \left( \frac{1540 m/s}{1540 m/s - 0.200 m/s}\right)\]
- Calcule para encontrar a frequência que retorna à fonte: 2.500.649 Hz.
Solução para (c)
- Identifique conhecidos:
- A frequência de batida é simplesmente o valor absoluto da diferença entre\(f_{s}\) e\(f_{obs}\) conforme declarado em:\[f_{B} = \vert f_{obs} - f_{s}\vert.\]
- Substitua os valores conhecidos:\[\vert 2,500,649 Hz - 2,500,000 Hz\vert\]
- Calcule para encontrar a frequência da batida: 649 Hz.
Discussão
Os desvios do Doppler são bem pequenos em comparação com a frequência original de 2,50 MHz. É muito mais fácil medir a frequência da batida do que medir a frequência do eco com uma precisão grande o suficiente para ver mudanças de algumas centenas de hertz em alguns megahertz. Além disso, as variações na frequência da fonte não afetam muito a frequência de batida, pois ambas\(f_{s}\)\(f_{obs}\) aumentariam ou diminuiriam. Essas mudanças se subtraem\(f_{B} = \vert f_{obs} - f_{s} \vert\).
APLICAÇÕES INDUSTRIAIS E OUTRAS DO ULTRASSOM
Aplicações industriais, de varejo e de pesquisa do ultrassom são comuns. Alguns são discutidos aqui. Os limpadores ultrassônicos têm muitos usos. Joias, peças usinadas e outros objetos com formas e fendas estranhas são imersos em um fluido de limpeza que é agitado com ultrassom, normalmente com cerca de 40 kHz de frequência. A intensidade é grande o suficiente para causar cavitação, responsável pela maior parte da ação de limpeza. Como as pressões de choque produzidas pela cavitação são grandes e bem transmitidas em um fluido, elas atingem pequenas fendas onde até mesmo um fluido de limpeza de baixa tensão superficial pode não penetrar.
O sonar é uma aplicação familiar do ultrassom. O sonar normalmente emprega frequências ultrassônicas na faixa de 30,0 a 100 kHz. Morcegos, golfinhos, submarinos e até alguns pássaros usam sonar ultrassônico. Os ecos são analisados para fornecer informações de distância e tamanho, tanto para orientação quanto para encontrar presas. Na maioria das aplicações de sonar, o som reflete muito bem porque os objetos de interesse têm uma densidade significativamente diferente do meio em que viajam. Quando o desvio do Doppler é observado, as informações de velocidade também podem ser obtidas. O sonar submarino pode ser usado para obter essas informações, e há evidências de que alguns morcegos também percebem a velocidade de seus ecos.
Da mesma forma, há uma variedade de dispositivos relativamente baratos que medem a distância cronometrando os ecos ultrassônicos. Muitas câmeras, por exemplo, usam essas informações para focar automaticamente. Algumas portas se abrem quando seus dispositivos de alcance ultrassônico detectam um objeto próximo, e certas luzes de segurança doméstica acendem quando seus guardas ultrassônicos observam o movimento. Também existem “fitas métricas” ultrassônicas para medir coisas como as dimensões da sala. Às vezes, as pias dos banheiros públicos são automatizadas com aparelhos de ultrassom para abrir e fechar as torneiras quando as pessoas lavam as mãos. Esses dispositivos reduzem a propagação de germes e podem conservar água.
O ultrassom é usado para testes não destrutivos na indústria e pelos militares. Como o ultrassom reflete bem em qualquer grande mudança na densidade, ele pode revelar rachaduras e vazios em sólidos, como asas de aeronaves, que são muito pequenos para serem vistos com raios-X. Por motivos semelhantes, o ultrassom também é bom para medir a espessura dos revestimentos, especialmente quando há várias camadas envolvidas.
A pesquisa básica em física do estado sólido emprega ultrassom. Sua atenuação está relacionada a várias características físicas, o que a torna uma sonda útil. Entre essas características estão as mudanças estruturais, como as encontradas em cristais líquidos, a transição de um material para uma fase supercondutora, bem como a densidade e outras propriedades.
Esses exemplos de usos do ultrassom têm como objetivo estimular o apetite dos curiosos, bem como ilustrar a física subjacente do ultrassom. Existem muitos outros aplicativos, como você mesmo pode descobrir facilmente.
Exercício\(\PageIndex{1}\)
Por que é possível usar o ultrassom tanto para observar um feto no útero quanto para destruir tumores cancerígenos no corpo?
- Responda
-
O ultrassom pode ser usado medicamente em diferentes intensidades. Intensidades mais baixas não causam danos e são usadas para imagens médicas. Intensidades mais altas podem pulverizar e destruir substâncias específicas no corpo, como tumores.
Resumo
- A impedância acústica é definida como\(Z = \rho v\), onde\(\rho\) é a densidade de um meio pelo qual o som viaja e\(v\) é a velocidade do som através desse meio.
- O coeficiente de reflexão de intensidade\(a\), uma medida da razão da intensidade da onda refletida em um limite entre dois meios em relação à intensidade da onda incidente, é dado por\(a = \frac{\left(Z_{2} - Z_{1}\right)^{2}}{\left(Z_{1} + Z_{2}\right)^{2}}\).
- O coeficiente de reflexão da intensidade é uma quantidade sem unidades.
Glossário
- impedância acústica
- propriedade do meio que dificulta a propagação das ondas sonoras
- coeficiente de reflexão de intensidade
- uma medida da razão da intensidade da onda refletida em um limite entre dois meios em relação à intensidade da onda incidente
- Ultrassonografia com desvio de Doppler
- uma técnica médica para detectar movimento e determinar a velocidade por meio do desvio Doppler de um eco


