12.1: Taxa de fluxo e sua relação com a velocidade
- Page ID
- 194158
objetivos de aprendizagem
Ao final desta seção, você poderá:
- Calcule a vazão.
- Defina unidades de volume.
- Descreva fluidos incompressíveis.
- Explique as consequências da equação da continuidade.
A taxa de fluxo\(Q\) é definida como o volume de fluido que passa por algum local através de uma área durante um período de tempo, conforme visto na Figura\(\PageIndex{1}\). Em símbolos, isso pode ser escrito como
\[Q = \dfrac{V}{t},\]
onde\(V\) está o volume, formiga\(t\) é o tempo decorrido.
A unidade SI para taxa de fluxo é\(m^3/s\), mas várias outras unidades\(Q\) são de uso comum. Por exemplo, o coração de um adulto em repouso bombeia sangue a uma taxa de 5,00 litros por minuto (L/min). Observe que um litro (L) é 1/1000 de um metro cúbico ou 1000 centímetros cúbicos (\(10^{-3} \, m^3\)ou\(10^3 \, cm\)). Neste texto, usaremos as unidades métricas mais convenientes para uma determinada situação.

Exemplo\(\PageIndex{1}\): Calculating Volume from Flow Rate: The Heart Pumps a Lot of Blood in a Lifetime
Quantos metros cúbicos de sangue o coração bombeia em uma vida útil de 75 anos, supondo que a vazão média seja de 5,00 L/min?
Estratégia
O tempo e a taxa de fluxo\(Q\) são fornecidos e, portanto, o volume\(V\) pode ser calculado a partir da definição da taxa de fluxo.
Solução
Resolver\(Q = V/t\) o volume dá
\[V = Qt. \nonumber \]
Substituir valores conhecidos rende
\[\begin{align*}V &= \left(\dfrac{5.00 \, L}{1 \, min}\right)(75 \, y)\left(\dfrac{1 \, m^3}{10^3 \, L}\right)(5.26 \times 10^5 \, \left(\dfrac{min}{y}\right) \\[5pt] &= 2.0 \times 10^5 \, m^3 \end{align*}\]
Discussão
Essa quantidade é de cerca de 200.000 toneladas de sangue. Para comparação, esse valor é equivalente a cerca de 200 vezes o volume de água contido em uma piscina olímpica de 50 m de 6 pistas.
A taxa de fluxo e a velocidade estão relacionadas, mas bem diferentes, quantidades físicas. Para deixar clara a distinção, pense na vazão de um rio. Quanto maior a velocidade da água, maior a vazão do rio. Mas a vazão também depende do tamanho do rio. Um rápido riacho de montanha carrega muito menos água do que o rio Amazonas no Brasil, por exemplo. A relação precisa entre a taxa de fluxo\(Q\) e a velocidade\(\overline{v}\) é
\[Q = A \overline{v},\]
onde\(A\) é a área da seção transversal e\( \overline{v}\) é a velocidade média. Essa equação parece lógica o suficiente. A relação nos diz que a taxa de fluxo é diretamente proporcional à magnitude da velocidade média (doravante denominada velocidade) e ao tamanho de um rio, tubulação ou outro conduíte. Quanto maior o conduíte, maior sua área de seção transversal. A figura\(\PageIndex{1}\) ilustra como essa relação é obtida. O cilindro sombreado tem um volume
\[V = Ad,\]
que passa do ponto\(P\) em um momento\(t\). Dividindo os dois lados desse relacionamento por\(t\) doações
\[\dfrac{V}{t} = \dfrac{Ad}{t}.\]
Notamos isso\(Q = V\t\) e a velocidade média é\(\overline{v} = d/t\). Assim, a equação se torna\(Q = A\overline{v}\).
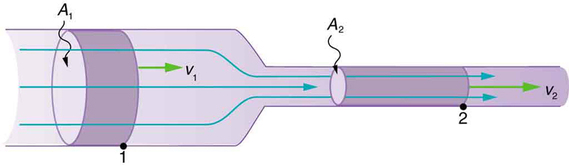
A figura\(\PageIndex{2}\) mostra um fluido incompressível fluindo ao longo de um tubo de raio decrescente. Como o fluido é incompressível, a mesma quantidade de fluido deve passar por qualquer ponto do tubo em um determinado momento para garantir a continuidade do fluxo. Nesse caso, como a área da seção transversal do tubo diminui, a velocidade deve necessariamente aumentar. Essa lógica pode ser estendida para dizer que a vazão deve ser a mesma em todos os pontos ao longo do tubo. Em particular, para os pontos 1 e 2,
\[Q_1 = Q_2\]
\[A_1\overline{v}_1 = A_2\overline{v}_2\]
Isso é chamado de equação de continuidade e é válido para qualquer fluido incompressível. As consequências da equação de continuidade podem ser observadas quando a água flui de uma mangueira para um bico de pulverização estreito: ela emerge com uma grande velocidade — esse é o propósito do bico. Por outro lado, quando um rio deságua em uma extremidade de um reservatório, a água diminui consideravelmente, talvez voltando a ganhar velocidade quando sai da outra extremidade do reservatório. Em outras palavras, a velocidade aumenta quando a área da seção transversal diminui e a velocidade diminui quando a área da seção transversal aumenta.
Como os líquidos são essencialmente incompressíveis, a equação da continuidade é válida para todos os líquidos. No entanto, os gases são compressíveis e, portanto, a equação deve ser aplicada com cuidado aos gases se eles forem submetidos à compressão ou expansão.
Exemplo\(\PageIndex{2}\): Calculating Fluid Speed: Speed Increases When a Tube Narrows
Um bocal com raio de 0,250 cm é conectado a uma mangueira de jardim com raio de 0,900 cm. A vazão através da mangueira e do bocal é de 0,500 L/s. Calcule a velocidade da água (a) na mangueira e (b) no bocal.
Estratégia
Podemos usar a relação entre a taxa de fluxo e a velocidade para encontrar as duas velocidades. Usaremos o subscrito 1 para a mangueira e 2 para o bocal.
Solução para (a)
Primeiro,\(Q = A\overline{v}\) resolvemos\(v_1\) e observamos que a área da seção transversal é\(A = \pi r^2\), produzindo
\[\overline{v}_1 = \dfrac{Q}{A_1} = \dfrac{Q}{\pi r_1^2}, \nonumber \]
Substituindo valores conhecidos e fazendo conversões unitárias apropriadas, rendimentos
\[\overline{v}_1 = \dfrac {(0.500 \, L/s)(10^{-3} m^3/L)}{\pi (9.00 \times 10^{-3}m)^2} = 1.96 \, m/s. \nonumber \]
Solução para (b)
Poderíamos repetir esse cálculo para encontrar a velocidade no bocal\(\overline{v}_2\), mas usaremos a equação da continuidade para fornecer uma visão um pouco diferente. Usando a equação que afirma
\[A_1\overline{v}_1 = A_2\overline{v}_2 \nonumber \]
resolvendo\(\overline{v}_2\) e substituindo\(\pi r^2\) os rendimentos da área da seção transversal
\[\overline{v}_2 = \dfrac{A_1}{A_2}\overline{v}_1 = \dfrac{\pi r_1^2}{\pi r_2^2}\overline{v}_1 = \dfrac{r_1^2}{r_2^2}\overline{v}_1. \nonumber \]
Substituindo valores conhecidos,
\[\overline{v}_2 = \dfrac{ (0.900 \, cm)^2}{(0.250 \, cm)^2} 1.96 \, m/s = 25.5 \, m/s. \nonumber \]
Discussão
Uma velocidade de 1,96 m/s é quase a certa para a água que sai de uma mangueira sem bico. O bocal produz um fluxo consideravelmente mais rápido simplesmente restringindo o fluxo para um tubo mais estreito.
A solução para a última parte do exemplo mostra que a velocidade é inversamente proporcional ao quadrado do raio do tubo, gerando grandes efeitos quando o raio varia. Podemos apagar uma vela a uma boa distância, por exemplo, apertando nossos lábios, enquanto soprar uma vela com a boca aberta é bastante ineficaz.
Em muitas situações, inclusive no sistema cardiovascular, ocorre a ramificação do fluxo. O sangue é bombeado do coração para as artérias que se subdividem em artérias menores (arteríolas) que se ramificam em vasos muito finos chamados capilares. Nessa situação, a continuidade do fluxo é mantida, mas é a soma das taxas de fluxo em cada um dos galhos em qualquer porção ao longo do tubo que é mantida. A equação da continuidade em uma forma mais geral se torna
\[n_1A_1\overline{v}_1 = n_2A_2\overline{v}_2,\]
onde\(n_1\) e\(n_2\) são o número de ramificações em cada uma das seções ao longo do tubo.
Exemplo\(\PageIndex{3}\): Calculating Flow Speed and Vessel Diameter: Branching in the Cardiovascular System
A aorta é o principal vaso sanguíneo através do qual o sangue sai do coração para circular pelo corpo. (a) Calcule a velocidade média do sangue na aorta se a taxa de fluxo for de 5,0 L/min. A aorta tem um raio de 10 mm. (b) O sangue também flui através de vasos sanguíneos menores, conhecidos como capilares. Quando a taxa de fluxo sanguíneo na aorta é de 5,0 L/min, a velocidade do sangue nos capilares é de cerca de 0,33 mm/s. Dado que o diâmetro médio de um capilar é\(8.0 \, \mu m\), calcule o número de capilares no sistema circulatório sanguíneo.
Estratégia
Podemos usar\(Q = A\overline{v}\) para calcular a velocidade do fluxo na aorta e, em seguida, usar a forma geral da equação de continuidade para calcular o número de capilares, como todas as outras variáveis são conhecidas.
Solução para (a)
A vazão é dada por\(Q = A\overline{v}\) ou\(\overline{v} = \frac{Q}{\pi r^2} \) para um recipiente cilíndrico.
Substituindo os valores conhecidos (convertidos em unidades de metros e segundos), obtém-se
\[\begin{align*} \overline{v} &= \dfrac{(5.0 \, L/min)(10^{-3} \, m^3/L)(1 \, min/60 \, s)}{\pi(0.010 \, m)^2} \\[5pt] &= 0.27 \, m/s. \end{align*}\]
Solução para (b)
Usando\(n_1A_1\overline{v}_1 = n_2A_2\overline{v}_1\), atribuindo o subscrito 1 à aorta e 2 aos capilares e resolvendo para\(n_2\) (o número de capilares), obtém-se a\(n_2 = \frac{n_1A_1\overline{v}_1}{A-2\overline{v}_2}.\) conversão de todas as quantidades em unidades de metros e segundos e a substituição na equação acima, obtém-se
\[\begin{align*} n_2 &= \dfrac{(1)(\pi)(10 \times 10^{-3} m)^2(0.27 \, m/s)}{(\pi)(4.0 \times 10^{-6} m)(0.33 \times 10^{-3} m/s)} \\[5pt] &= 5.0 \times 10^9 \, capillaries.\end{align*}\]
Discussão
Observe que a velocidade do fluxo nos capilares é consideravelmente reduzida em relação à velocidade na aorta devido ao aumento significativo na área total da seção transversal nos capilares. Essa baixa velocidade deve permitir tempo suficiente para que a troca efetiva ocorra, embora seja igualmente importante que o fluxo não fique estacionário para evitar a possibilidade de coagulação. Esse grande número de capilares no corpo parece razoável? No músculo ativo, encontramos cerca de 200 capilares por\(mm^3\), ou cerca\(200 \times 10^6\) de 1 kg de músculo. Para 20 kg de músculo, isso equivale a cerca de\(4 \times 10^9\) capilares. × 10 9
Resumo
- A taxa de fluxo\(Q\) é definida como o volume\(V\) que passa de um ponto no tempo\(t\), ou\(Q = \frac{V}{t}\) onde\(V\) está o volume e\(t\) o tempo.
- A unidade de volume SI é\(m^3\).
- Outra unidade comum é o litro (L), que é\(10^{-3}m^3\)
- A taxa de fluxo e a velocidade estão relacionadas por\(Q = A\overline{v}\) onde\(A\) está a área da seção transversal do fluxo e\(v\) sua velocidade média.
- Para fluidos incompressíveis, a vazão em vários pontos é constante. Ou seja,
\[Q_1 = Q_2\]
\[A_1\overline{v}_1 = A_2\overline{v}_2\]
\[n_1A_1\overline{v}_1 = n_2A_2\overline{v}_2\]
Glossário
- taxa de fluxo
- abreviado Q, é o volume V que passa por um determinado ponto durante um tempo t, ou Q = v/t
- litro
- uma unidade de volume, igual a 10 −3 m 3


