11.7: Princípio de Arquimedes
- Page ID
- 195254
Objetivos de
Ao final desta seção, você poderá:
- Defina a força de empuxo.
- Declare o princípio de Arquimedes.
- Entenda por que objetos flutuam ou afundam.
- Entenda a relação entre densidade e o princípio de Arquimedes.
Quando você se levanta depois de descansar em um banho quente, seus braços ficam estranhamente pesados. Isso ocorre porque você não tem mais o suporte flutuante da água. De onde vem essa força de empuxo? Por que algumas coisas flutuam e outras não? Os objetos que afundam recebem algum suporte do fluido? Seu corpo está impulsionado pela atmosfera ou apenas os balões de hélio são afetados (Figura\(\PageIndex{1}\))?

As respostas a todas essas perguntas e muitas outras são baseadas no fato de que a pressão aumenta com a profundidade de um fluido. Isso significa que a força ascendente na parte inferior de um objeto em um fluido é maior do que a força descendente na parte superior do objeto. Há uma rede ascendente ou força de empuxo em qualquer objeto em qualquer fluido (Figura\(\PageIndex{2}\)). Se a força de empuxo for maior que o peso do objeto, o objeto subirá à superfície e flutuará. Se a força de empuxo for menor que o peso do objeto, o objeto afundará. Se a força de empuxo for igual ao peso do objeto, o objeto permanecerá suspenso nessa profundidade. A força de empuxo está sempre presente se o objeto flutua, afunda ou está suspenso em um fluido.
Definição: Força de empuxo
A força de empuxo é a força total ascendente em qualquer objeto em qualquer fluido.
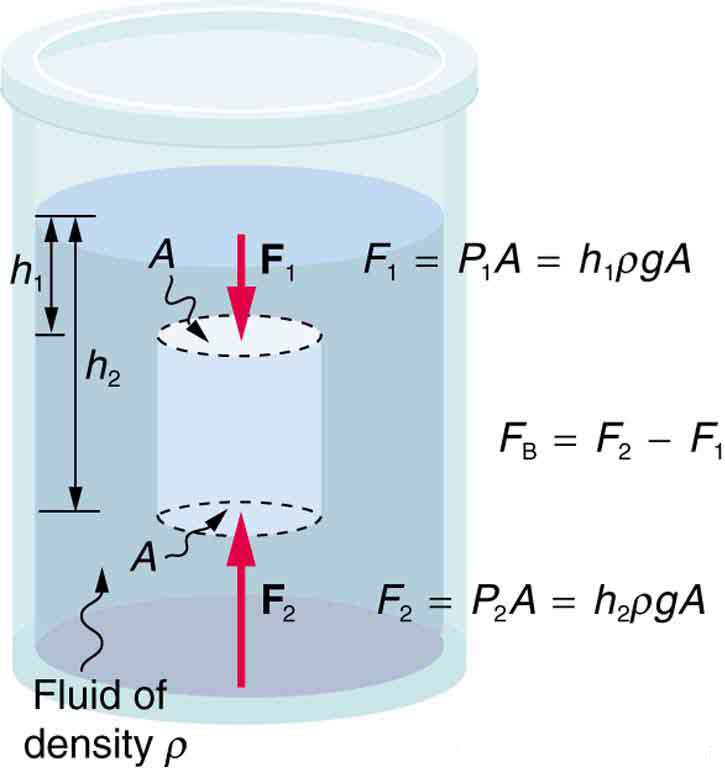
Quão grande é essa força de empuxo? Para responder a essa pergunta, pense no que acontece quando um objeto submerso é removido de um fluido, como na Figura\(\PageIndex{3}\).
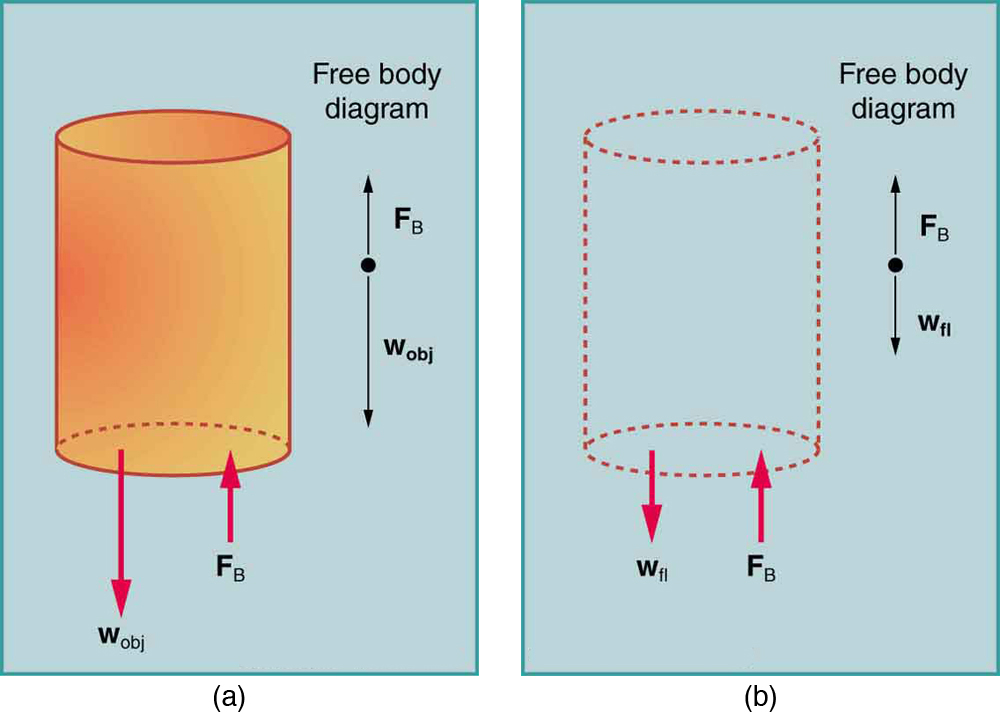
O espaço ocupado é preenchido por um fluido com peso\(w_{fl}\). Esse peso é suportado pelo fluido circundante e, portanto\(w_{fl}\), a força de empuxo deve ser igual ao peso do fluido deslocado pelo objeto. É uma homenagem à genialidade do matemático e inventor grego Arquimedes (cerca de 287-212 a.C.) que ele tenha afirmado esse princípio muito antes de os conceitos de força estarem bem estabelecidos. Em palavras, o princípio de Arquimedes é o seguinte: A força de empuxo em um objeto é igual ao peso do fluido que ele desloca. Em forma de equação, o princípio de Arquimedes é
\[F_B = w_{fl},\]
onde\(F_B\) está a força de empuxo e\(w_{fl}\) é o peso do fluido deslocado pelo objeto. O princípio de Arquimedes é válido em geral, para qualquer objeto em qualquer fluido, seja parcial ou totalmente submerso.
Princípio de Arquimedes
De acordo com esse princípio, a força de empuxo em um objeto é igual ao peso do fluido que ele desloca. Em forma de equação, o princípio de Arquimedes\(F_B\) é\[F_B = w_{fl},\] onde está a força de empuxo e\(w_{fl}\) é o peso do fluido deslocado pelo objeto.
Humm... Os trajes de banho corporais de alta tecnologia foram introduzidos em 2008 em preparação para as Olimpíadas de Pequim. Uma preocupação (e regra internacional) era que esses trajes não deveriam oferecer nenhuma vantagem de flutuabilidade. Como você acha que essa regra poderia ser verificada?
Fazendo conexões: investigação para levar para casa
A densidade da folha de alumínio é 2,7 vezes a densidade da água. Pegue um pedaço de papel alumínio, enrole-o em uma bola e coloque-o na água. Afunda? Por que ou por que não? Você pode fazê-lo afundar?
Flutuando e afundando
Coloque um pedaço de argila na água. Vai afundar. Em seguida, molde o pedaço de argila na forma de um barco e ele flutuará. Por causa de sua forma, o barco desloca mais água do que o caroço e experimenta uma força de empuxo maior. O mesmo se aplica aos navios de aço.
Exemplo\(\PageIndex{1}\): Calculating buoyant force: dependency on shape
- Calcule a força de empuxo em 10.000 toneladas métricas\((1.00 \times 10^7 \, kg)\) de aço sólido completamente submerso na água e compare isso com o peso do aço.
- Qual é a força máxima de empuxo que a água poderia exercer sobre esse mesmo aço se fosse moldada em um barco que pudesse deslocar\(1.00 \times 10^5 \, m^3\) a água?
Estratégia para (a)
Para encontrar a força de empuxo, precisamos encontrar o peso da água deslocada. Podemos fazer isso usando as densidades de água e aço fornecidas em [link]. Observamos que, como o aço está completamente submerso, seu volume e o volume da água são os mesmos. Depois de sabermos o volume da água, podemos encontrar sua massa e peso.
Solução para (a)
Primeiro, usamos a definição de densidade\(\rho = \frac{m}{V}\) para encontrar o volume do aço e depois substituímos os valores por massa e densidade. Isso dá
\[V_{st} = \dfrac{m_{st}}{\rho_{st}} = \dfrac{1.00 \times 10^7 \, kg}{7.8 \times 10^3 \, kg/m^3} = 1.28 \times 10^3 \, m^3.\]
Como o aço está completamente submerso, esse também é o volume de água deslocado\(V_W\). Agora podemos encontrar a massa de água deslocada da relação entre seu volume e densidade, ambos conhecidos. Isso dá
\[m_W = \rho_WV_W = (1.000 \times 10^3 \, kg/m^3)(1.28 \times 10^3 \, m^3)\]
\[= 1.3 \times 10^6 \, kg.\]
Pelo princípio de Arquimedes, o peso da água deslocada é\(m_Wg\), então a força de empuxo é
\[F_B = w_W = m_Wg = (1.28 \times 10^6\space kg)(9.80 \, m/s^2)\]
\[= 1.3 \times 10^7 \, N.\]
O peso do aço é\(m_W g = 9.80 \times 10^7 \, N\),
que é muito maior do que a força de empuxo, então o aço permanecerá submerso. Observe que a força de empuxo é arredondada para dois dígitos porque a densidade do aço é dada a apenas dois dígitos.
Estratégia para (b)
Aqui temos o volume máximo de água que o barco de aço pode deslocar. A força de empuxo é o peso desse volume de água.
Solução para (b)
A massa de água deslocada é encontrada a partir de sua relação com a densidade e o volume, ambos conhecidos. Ou seja,
\[m_W = \rho_WV_W = (1.000 \times 10^3 \, kg/m^3)(1.00 \times 10^5 \, m^3)\]
\[= 9.80 \times 10^8 \, kg.\]
A força máxima de empuxo é o peso dessa quantidade de água, ou
\[F_B = w_W = m_W g = (1.00 \times 10^8 \, kg)(9.80 \, m/s^2)\]
\[= \times 10^8 \, N.\]
Discussão
A força máxima de empuxo é dez vezes o peso do aço, o que significa que o navio pode carregar uma carga nove vezes seu próprio peso sem afundar.
Fazendo conexões: investigação para levar para casa
- Um pedaço de papel alumínio doméstico tem 0,016 mm de espessura. Use um pedaço de papel alumínio que meça 10 cm por 15 cm. (a) Qual é a massa dessa quantidade de papel alumínio? (b) Se a folha for dobrada para obter quatro lados e clipes de papel ou arruelas forem adicionados a esse “barco”, qual formato do barco permitiria que ele retivesse a maior “carga” quando colocado na água? Teste sua previsão.
Densidade e Princípio de Arquimedes
A densidade desempenha um papel crucial no princípio de Arquimedes. A densidade média de um objeto é o que, em última análise, determina se ele flutua. Se sua densidade média for menor que a do fluido circundante, ele flutuará. Isso ocorre porque o fluido, com maior densidade, contém mais massa e, portanto, mais peso no mesmo volume. A força de empuxo, que é igual ao peso do fluido deslocado, é, portanto, maior que o peso do objeto. Da mesma forma, um objeto mais denso que o fluido afundará.
A extensão em que um objeto flutuante está submerso depende de como a densidade do objeto está relacionada à do fluido. Na Figura\(\PageIndex{4}\), por exemplo, o navio descarregado tem uma densidade menor e menos está submerso em comparação com o mesmo navio carregado. Podemos derivar uma expressão quantitativa para a fração submersa considerando a densidade. A fração submersa é a razão entre o volume submerso e o volume do objeto, ou
\[fraction \, submerged = \dfrac{V_{sub}}{V_{obj}} = \dfrac{V_{fl}}{V_{obj}}.\]
O volume submerso é igual ao volume de fluido deslocado, que chamamos\(V_{fl}\). Agora podemos obter a relação entre as densidades\(\rho = \frac{m}{V}\) substituindo-as na expressão. Isso dá
\[\dfrac{V_{fl}}{V_{obj}} = \dfrac{m_{fl}/\rho_{fl}}{m_{obj}/\overline{\rho}_{obj}},\]
onde\(\overline{\rho}_{obj}\) é a densidade média do objeto e\(\rho_{fl}\) é a densidade do fluido. Como o objeto flutua, sua massa e a do fluido deslocado são iguais e, portanto, elas se cancelam da equação, deixando
\[fraction \, submerged = \dfrac{\overline{\rho}_{obj}}{\rho_{fl}}.\]

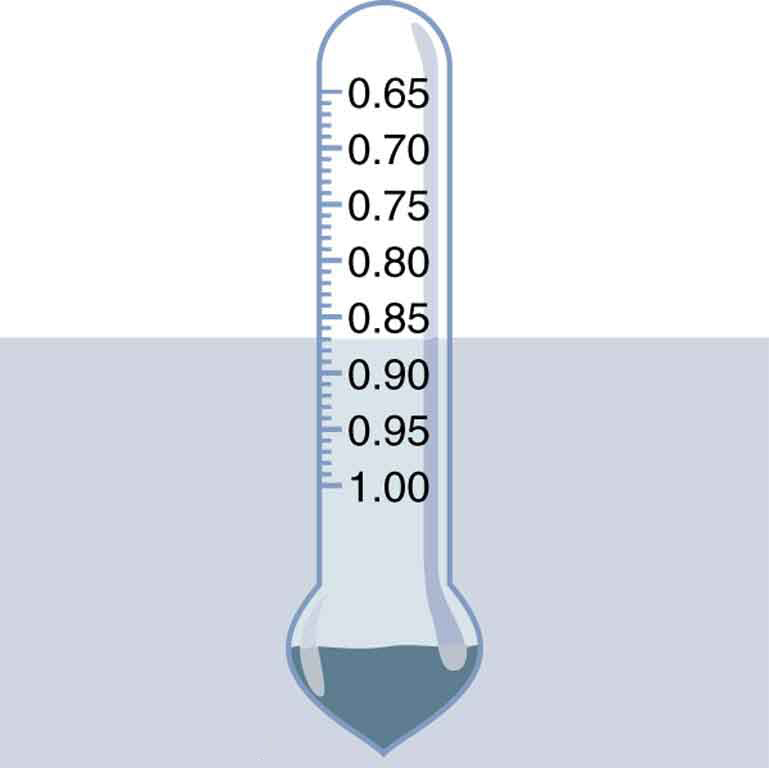
Usamos essa última relação para medir densidades. Isso é feito medindo a fração de um objeto flutuante que está submerso, por exemplo, com um hidrômetro. É útil definir a razão entre a densidade de um objeto e um fluido (geralmente água) como gravidade específica:
\[specific \, gravity = \dfrac{\overline{\rho}}{\rho_W},\]onde\(\overline{\rho}\) é a densidade média do objeto ou substância e\(\rho_W\) é a densidade da água a 4,00°C. A gravidade específica é adimensional, independente de qualquer unidade usada\(\rho\). Se um objeto flutua, sua gravidade específica é menor que um. Se afundar, sua gravidade específica é maior que um. Além disso, a fração de um objeto flutuante que está submerso é igual à sua gravidade específica. Se a gravidade específica de um objeto for exatamente 1, ele permanecerá suspenso no fluido, nem afundando nem flutuando. Os mergulhadores tentam obter esse estado para que possam pairar na água. Medimos a gravidade específica dos fluidos, como ácido da bateria, fluido do radiador e urina, como um indicador de sua condição. Um dispositivo para medir a gravidade específica é mostrado na Figura\(\PageIndex{5}\).
Definição: Gravidade específica
A gravidade específica é a razão entre a densidade de um objeto e um fluido (geralmente água).
Exemplo\(\PageIndex{2}\): Calculating Average Density: Floating Woman
Suponha que uma mulher de 60,0 kg flutue em água doce com\(97.0\%\) seu volume submerso quando seus pulmões estão cheios de ar. Qual é a densidade média dela?
Estratégia
Podemos encontrar a densidade da mulher resolvendo a equação
\[fraction \, submerged = \dfrac{\overline{\rho}_{obj}}{\rho_{fl}}\]
para a densidade do objeto. Isso rende
\[\overline{\rho}_{obj} = \overline{\rho}_{person} = (fraction \, submerged) \cdot \rho_{fl}.\]
Conhecemos tanto a fração submersa quanto a densidade da água, então podemos calcular a densidade da mulher.
Solução
Inserindo os valores conhecidos na expressão de sua densidade, obtemos
\[\overline{\rho}_{person} = 0.970 \cdot \left(10^3 \, \dfrac{kg}{m^3}\right) = 970 \, \dfrac{kg}{m^3}.\]
Discussão
Sua densidade é menor que a densidade do fluido. Esperamos isso porque ela flutua. A densidade corporal é um indicador da porcentagem de gordura corporal de uma pessoa, de interesse em diagnósticos médicos e treinamento atlético. (Veja a Figura\(\PageIndex{7}\))
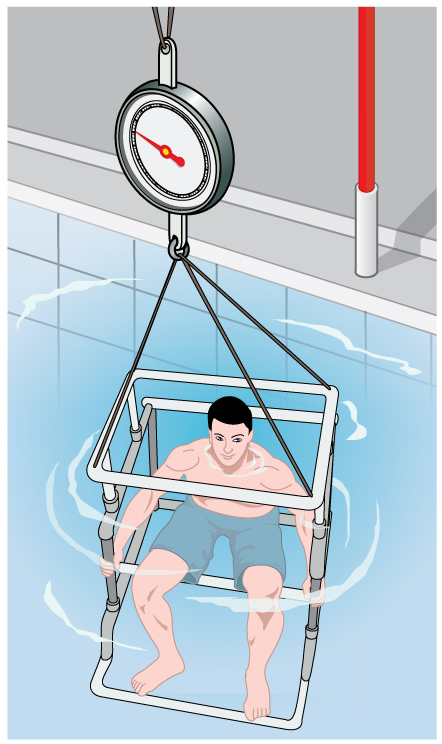
Há muitos exemplos óbvios de objetos ou substâncias de baixa densidade flutuando em fluidos de alta densidade: óleo sobre água, um balão de ar quente, um pouco de cortiça no vinho, um iceberg e cera quente em uma “lâmpada de lava”, para citar alguns. Exemplos menos óbvios incluem lava subindo em um vulcão e cadeias de montanhas flutuando na crosta de maior densidade e no manto abaixo delas. Até a Terra aparentemente sólida tem características fluidas.
Mais medições de densidade
Uma das técnicas mais comuns para determinar a densidade é mostrada na Figura\(\PageIndex{7}\). Um objeto, aqui uma moeda, é pesado no ar e depois pesado novamente enquanto está submerso em um líquido. A densidade da moeda, uma indicação de sua autenticidade, pode ser calculada se a densidade do fluido for conhecida. Essa mesma técnica também pode ser usada para determinar a densidade do fluido se a densidade da moeda for conhecida. Todos esses cálculos são baseados no princípio de Arquimedes.
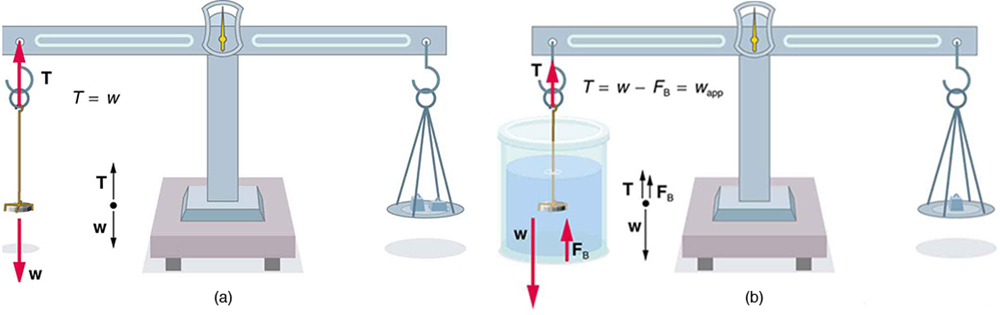
O princípio de Arquimedes afirma que a força de empuxo no objeto é igual ao peso do fluido deslocado. Isso, por sua vez, significa que o objeto parece pesar menos quando submerso; chamamos essa medida de peso aparente do objeto. O objeto sofre uma aparente perda de peso igual ao peso do fluido deslocado. Alternativamente, em balanças que medem a massa, o objeto sofre uma aparente perda de massa igual à massa do fluido deslocado. Isso é
\[apparent \, weight \, loss = weight \, of \, fluid \, displaced\]ou
\[apparent \, mass \, loss = mass \, of \, fluid \, displaced.\]
O exemplo a seguir ilustra o uso dessa técnica.
Exemplo\(\PageIndex{3}\): Calculating Density: Is the Coin Authentic?
A massa de uma moeda grega antiga é determinada no ar em 8.630 g. Quando a moeda está submersa na água, conforme mostrado na Figura\(\PageIndex{7}\), sua massa aparente é 7.800 g. Calcule sua densidade, dado que a água tem uma densidade de\(1.000 \, g/m^3\)
e que os efeitos causados pelo fio que suspende a moeda são insignificantes.
Estratégia
Para calcular a densidade da moeda, precisamos de sua massa (que é dada) e seu volume. O volume da moeda é igual ao volume de água deslocada. O volume de água deslocado\(\rho = \frac{m}{V}\) para\(V\).
Solução
O volume de água é\(V_W = \frac{m_W}{\rho_W}\) onde\(m_W\) está a massa de água deslocada. Conforme observado, a massa da água deslocada é igual à perda aparente de massa, que é\(m_W = 8.630 \, g - 7.800 \, g = 0.830 \, g\). Assim, o volume de água é\(V_W = \frac{0.830 \, g}{1.000 \, g/cm^3} = 0.830 \, cm^3\). Esse também é o volume da moeda, já que ela está completamente submersa. Agora podemos encontrar a densidade da moeda usando a definição de densidade:
\[\rho_c = \dfrac{m_c}{V_c} = \dfrac{8.630 \, g}{0.830 \, cm^3} = 10.4 \, g/cm^3.\]
Discussão
Você pode ver no [link] que essa densidade é muito próxima à da prata pura, apropriada para esse tipo de moeda antiga. A maioria das falsificações modernas não são prata pura.
Isso nos leva de volta ao princípio de Arquimedes e como ele surgiu. Segundo a história, o rei de Siracusa deu a Arquimedes a tarefa de determinar se o fabricante da coroa real estava fornecendo uma coroa de ouro puro. A pureza do ouro é difícil de determinar pela cor (ele pode ser diluído com outros metais e ainda parecer tão amarelo quanto o ouro puro), e outras técnicas analíticas ainda não haviam sido concebidas. Mesmo os povos antigos, no entanto, perceberam que a densidade do ouro era maior do que a de qualquer outra substância conhecida na época. Arquimedes supostamente agonizou com sua tarefa e se inspirou um dia enquanto estava nos banhos públicos, ponderando sobre o apoio que a água dava a seu corpo. Ele inventou seu princípio agora famoso, viu como aplicá-lo para determinar a densidade e correu nu pelas ruas de Siracusa gritando “Eureka!” (A palavra grega significa “eu o encontrei”). Comportamento semelhante pode ser observado em físicos contemporâneos de tempos em tempos!
Explorações PhET: Flutuabilidade
Quando os objetos flutuarão e quando afundarão? Saiba como a flutuabilidade funciona com blocos. As setas mostram as forças aplicadas e você pode modificar as propriedades dos blocos e do fluido.
Resumo
- A força de empuxo é a força ascendente líquida em qualquer objeto em qualquer fluido. Se a força de empuxo for maior que o peso do objeto, o objeto subirá à superfície e flutuará. Se a força de empuxo for menor que o peso do objeto, o objeto afundará. Se a força de empuxo for igual ao peso do objeto, o objeto permanecerá suspenso nessa profundidade. A força de empuxo está sempre presente se o objeto flutua, afunda ou está suspenso em um fluido.
- O princípio de Arquimedes afirma que a força de empuxo em um objeto é igual ao peso do fluido que ele desloca.
- A gravidade específica é a razão entre a densidade de um objeto e um fluido (geralmente água).
Glossário
- Princípio de Arquimedes
- a força de empuxo em um objeto é igual ao peso do fluido que ele desloca
- força de empuxo
- a força ascendente líquida em qualquer objeto em qualquer fluido
- gravidade específica
- a razão entre a densidade de um objeto e um fluido (geralmente água)


