Skip to main content
Global

11.2: Densidade

  1. Last updated
  2. Save as PDF
  • Page ID
    195260

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Defina densidade.
    • Calcule a massa de um reservatório a partir de sua densidade.
    • Compare e contraste as densidades de várias substâncias.

    O que pesa mais, uma tonelada de penas ou uma tonelada de tijolos? Esse velho enigma brinca com a distinção entre massa e densidade. Uma tonelada é uma tonelada, é claro; mas os tijolos têm uma densidade muito maior do que as penas, e por isso somos tentados a pensar neles como mais pesados (Figura\(\PageIndex{1}\)).

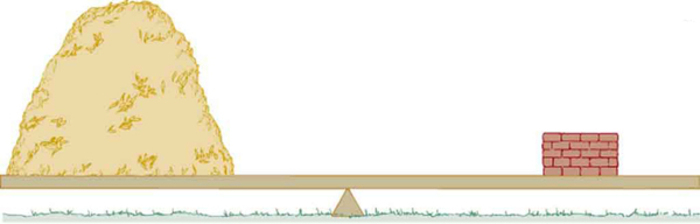
    Uma pilha de penas medindo uma tonelada e uma tonelada de tijolos são colocadas em cada lado de uma prancha balanceada em um pequeno suporte.
    Figura\(\PageIndex{1}\): Uma tonelada de penas e uma tonelada de tijolos têm a mesma massa, mas as penas formam uma pilha muito maior porque têm uma densidade muito menor.

    A densidade, como você verá, é uma característica importante das substâncias. É crucial, por exemplo, para determinar se um objeto afunda ou flutua em um fluido.

    Definição: Densidade

    A densidade é a massa por unidade de volume.

    \[\rho = \dfrac{m}{V},\label{density}\]

    onde a letra grega\(\rho\) (rho) é o símbolo da densidade,\(m\) é a massa e\(V\) é o volume ocupado pela substância.

    No enigma das penas e dos tijolos, as massas são as mesmas, mas o volume ocupado pelas penas é muito maior, pois sua densidade é muito menor. A unidade de densidade SI é\(kg/m^3\), valores representativos são fornecidos na Tabela\(\PageIndex{1}\). O sistema métrico foi originalmente concebido para que a água tivesse uma densidade de\(1 \, g/cm^3\), equivalente\(10^3 \, kg/m^3\) a. Assim, a unidade de massa básica, o quilograma, foi inicialmente concebida para ser a massa de 1000 mL de água, que tem um volume de\(1000 \, cm^3\).

    Tabela\(\PageIndex{1}\): Densidades de várias substâncias
    Substância \(\rho(10^3\frac{kg}{m^3} \, or \, \frac{g}{mL})\) Substância \(\rho(10^3\frac{kg}{m^3} \, or \, \frac{g}{mL})\) Substância \(\rho(10^3\frac{kg}{m^3} \, or \, \frac{g}{mL})\)
    \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” rowspan="1" style="text-align:center; "> Sólidos \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” rowspan="1" style="text-align:center; "> Líquidos \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” rowspan="1" style="text-align:center; "> Gases
    Alumínio \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">2.7 Água (4ºC) \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">1.000 Ar \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">\(1.29 \times 10^{-3}\)
    Latão \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">8.44 Sangue \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">1,05 Dióxido de carbono \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">\(1.98 \times 10^{-3}\)
    Cobre (médio) \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">8.8 Água do mar \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">1.025 Monóxido de carbono \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">\(1.25 \times 10^{-3}\)
    Ouro \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">19.32 Mercúrio \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">13.6 Hidrogênio \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">\(0.090 \times 10^{-3}\)
    Ferro ou aço \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">7.8 Álcool etílico \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">0.79 Hélio \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">\(0.18 \times 10^{-3}\)
    Liderar \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">11.3 Gasolina \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">0,68 Metano \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">\(0.72 \times 10^{-3}\)
    Poliestireno \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">0.10 Glicerina \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">1.26 Azoto \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">\(1.25 \times 10^{-3}\)
    Tungstênio \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">19.30 Azeite \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">0.92 Óxido nitroso \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">\(1.98 \times 10^{-3}\)
    Urânio \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">18,70   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; "> Oxigênio \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">\(1.43 \times 10^{-3}\)
    Concreto \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">2,30—3,0   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; "> Vapor\(100^o\) \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">\(0.60 \times 10^{-3}\)
    Cortiça \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">0.24   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">
    Vidro, comum (médio) \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">2.6   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">
    Granito \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">2.7   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">
    Crosta terrestre \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">3.3   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">
    Madeira \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">0,3—0,9   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">
    Gelo (0°C) \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">0.917   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">
    Osso \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">1,7—2,0   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">   \ (\ rho (10^3\ frac {kg} {m^3}\, ou\,\ frac {g} {mL})\)” style="text-align:center; ">

    Como você pode ver ao examinar a Tabela\(\PageIndex{1}\), a densidade de um objeto pode ajudar a identificar sua composição. A densidade do ouro, por exemplo, é cerca de 2,5 vezes a densidade do ferro, que é cerca de 2,5 vezes a densidade do alumínio. A densidade também revela algo sobre a fase da matéria e sua subestrutura. Observe que as densidades de líquidos e sólidos são aproximadamente comparáveis, consistentes com o fato de que seus átomos estão em contato próximo. As densidades dos gases são muito menores do que as dos líquidos e sólidos, porque os átomos dos gases são separados por grandes quantidades de espaço vazio.

    EXPERIMENTE PARA LEVAR PARA CASA AÇÚCAR E SAL

    Uma pilha de açúcar e uma pilha de sal parecem bem parecidas, mas o que pesa mais? Se os volumes de ambas as pilhas forem iguais, qualquer diferença de massa se deve às suas diferentes densidades (incluindo o espaço aéreo entre os cristais). Qual você acha que tem a maior densidade? Quais valores você encontrou? Qual método você usou para determinar esses valores?

    Exemplo\(\PageIndex{1}\): Calculating the Mass of a Reservoir From Its Volume

    Um reservatório tem uma área de superfície\(50 \, km^2\) e uma profundidade média de 40,0 m. Que massa de água é mantida atrás da barragem? (Veja a Figura\(\PageIndex{2}\) para ver uma vista de um grande reservatório — o local da Barragem das Três Gargantas no rio Yangtze, no centro da China.)

    Fotografia da Barragem das Três Gargantas no centro da China.
    Figura\(\PageIndex{2}\): Barragem das Três Gargantas no centro da China. Quando concluída em 2008, ela se tornou a maior usina hidrelétrica do mundo, gerando energia equivalente à gerada por 22 usinas nucleares de tamanho médio. A barragem de concreto tem 181 m de altura e 2,3 km de diâmetro. O reservatório feito por essa barragem tem 660 km de extensão. Mais de 1 milhão de pessoas foram deslocadas com a criação do reservatório. (crédito: Le Grand Portage)

    Estratégia

    Podemos calcular o volume\(V\) do reservatório a partir de suas dimensões e encontrar a densidade da água\(\rho\) na Tabela\(\PageIndex{1}\). Então, a massa\(m\) pode ser encontrada a partir da definição de densidade (Equação\ ref {densidade}).

    Solução

    Resolvendo a equação\ ref {densidade} para\(m\) dados

    \[m = \rho V. \nonumber\]

    O volume\(V\) do reservatório é sua área de superfície\(A\) vezes sua profundidade média\(h\):

    \[\begin{align*} V &= Ah \\[5pt] &= (50.0 \, km^2)(40.0 \, m) \\[5pt] &= \left [ (50.0 \, km^2)\left(\frac{10^3 \, m}{1 \, km}\right )\right ](40.0 \, m) \\[5pt] &= 2.00 \times 10^9 \, m^3 \end{align*}\]

    A densidade da água\(\rho\) da mesa\(\PageIndex{1}\) é\(1.000 \times 10^3 \, kg/m^3 \). Substituir “\(V\)e”\(\rho\) na expressão “massa” dá

    \[\begin{align*} m &= (1.00 \times 10^3 \, kg/m^3)(2.00 \times 10^9 \, m^3) \\[5pt] &= 2.00 \times 10^{12} \, kg.\end{align*}\]

    Discussão

    Um grande reservatório contém uma massa muito grande de água. Neste exemplo, o peso da água no reservatório é\(mg = 1.96 \times 10^{13} \, N\), onde\(g\) está a aceleração devido à gravidade da Terra (cerca de\(9.80 \, m/s^2\)). É razoável perguntar se a barragem deve fornecer uma força igual a esse tremendo peso. A resposta é não. Como veremos nas seções a seguir, a força que a barragem deve fornecer pode ser muito menor do que o peso da água que ela retém.

    Resumo

    • Densidade é a massa por unidade de volume de uma substância ou objeto. Na forma de equação, a densidade é definida como\[\rho = \dfrac{m}{V}. n\nonumber\]
    • A unidade de densidade SI é\(kg/m^3\).

    Glossário

    densidade
    a massa por unidade de volume de uma substância ou objeto