7.E: Trabalho, energia e recursos energéticos (exercício)
- Page ID
- 194347
Perguntas conceituais
7.1: Trabalho: a definição científica
1. Dê um exemplo de algo que consideramos trabalho em circunstâncias cotidianas que não é trabalho no sentido científico. A energia é transferida ou alterada de forma em seu exemplo? Em caso afirmativo, explique como isso é feito sem trabalhar.
2. Dê um exemplo de uma situação em que há uma força e um deslocamento, mas a força não funciona. Explique por que isso não funciona.
3. Descreva uma situação em que uma força é exercida por muito tempo, mas não funciona. Explique.
7.2: Energia Cinética e o Teorema da Energia do Trabalho
4. A pessoa na Figura trabalha no cortador de grama. Sob quais condições o cortador ganharia energia? Em que condições perderia energia?
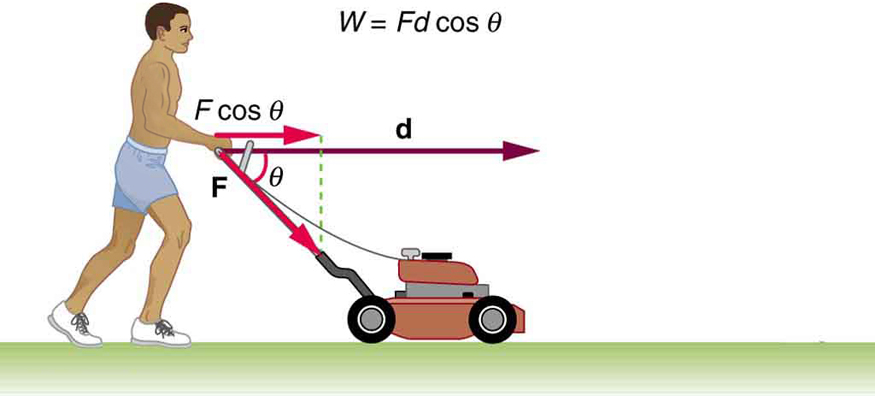
5. O trabalho realizado em um sistema coloca energia nele. O trabalho realizado por um sistema remove energia dele. Dê um exemplo para cada afirmação.
6. Ao resolver a velocidade no Exemplo, mantivemos apenas a raiz positiva. Por quê?
7.3: Energia potencial gravitacional
7. No exemplo, calculamos a velocidade final de uma montanha-russa que desceu 20 m de altura e teve uma velocidade inicial de 5 m/s em declive. Suponha que a montanha-russa tivesse tido uma velocidade inicial de 5 m/s para cima e, em vez disso, subisse, parasse e depois caísse de volta para um ponto final 20 m abaixo do início. Nesse caso, descobriríamos que sua velocidade final é igual à velocidade inicial. Explique em termos de conservação de energia.
8. O trabalho que você faz em um livro ao levantá-lo em uma prateleira depende do caminho percorrido? Sobre o tempo gasto? Na altura da prateleira? Na massa do livro?
7.4: Forças conservadoras e energia potencial
9. O que é uma força conservadora?
10. A força exercida por uma prancha de mergulho é conservadora, desde que o atrito interno seja insignificante. Supondo que o atrito seja insignificante, descreva as mudanças na energia potencial de uma prancha de mergulho à medida que um nadador mergulha nela, começando pouco antes de o nadador pisar na prancha até logo após seus pés saírem dela.
11. Defina energia mecânica. Qual é a relação da energia mecânica com as forças não conservadoras? O que acontece com a energia mecânica se apenas forças conservadoras atuarem?
12. Qual é a relação da energia potencial com a força conservadora?
7.6: Conservação de energia
13. Considere o cenário a seguir. Um carro cujo atrito não é desprezível acelera do repouso descendo uma colina, ficando sem gasolina após uma curta distância. O motorista deixa o carro descer a colina mais abaixo, depois subir e passar por cima de uma pequena crista. Ele então desce aquela colina até um posto de gasolina, onde ele freia até parar e enche o tanque com gasolina. Identifique as formas de energia que o carro tem e como elas são alteradas e transferidas nesta série de eventos. (Veja a Figura.)
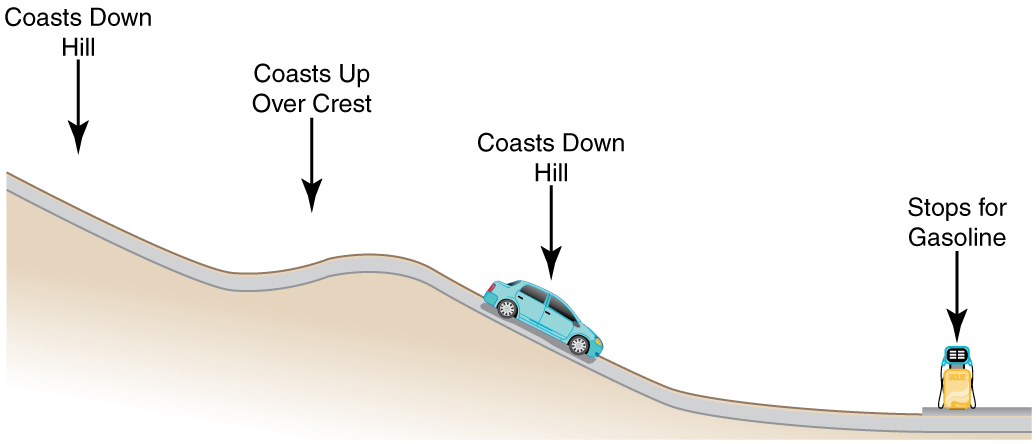
Um carro com atrito não desprezível desce uma colina, sobre uma pequena crista, depois desce novamente e para em um posto de gasolina.
14. Descreva as transferências e transformações de energia de um dardo, começando do ponto em que um atleta pega o dardo e terminando quando o dardo é preso no chão após ser lançado.
15. Dispositivos com eficiências de menos de um violam a lei de conservação de energia? Explique.
16. Liste quatro formas ou tipos diferentes de energia. Dê um exemplo de conversão de cada um desses formulários para outro formulário.
17. Liste as conversões de energia que ocorrem ao andar de bicicleta.
7.7: Potência
18. A maioria dos aparelhos elétricos é avaliada em watts. Essa classificação depende de quanto tempo o aparelho está ligado? (Quando desligado, é um dispositivo de zero watts.) Explique em termos da definição de poder.
19. Explique, em termos da definição de potência, por que o consumo de energia às vezes é listado em quilowatts-hora em vez de joules. Qual é a relação entre essas duas unidades de energia?
20. Uma faísca de eletricidade estática, como a que você pode receber de uma maçaneta em um dia frio e seco, pode transportar algumas centenas de watts de potência. Explique por que você não se machucou por essa faísca.
7.8: Trabalho, energia e poder em humanos
21. Explique por que é mais fácil escalar uma montanha em um caminho em zigue-zague do que em linha reta na lateral. Seu aumento na energia potencial gravitacional é o mesmo em ambos os casos? Seu consumo de energia é o mesmo em ambos?
22. Você trabalha no mundo exterior quando esfrega as mãos para aquecê-las? Qual é a eficiência dessa atividade?
23. O tremor é uma resposta involuntária à baixa temperatura corporal. Qual é a eficiência do corpo ao tremer, e esse é um valor desejável?
24. Discuta a eficácia relativa da dieta e dos exercícios na perda de peso, observando que a maioria das atividades atléticas consome energia alimentar a uma taxa de 400 a 500 W, enquanto uma única xícara de iogurte pode conter 1360 kJ (325 kcal). Especificamente, é provável que o exercício por si só seja suficiente para perder peso? Você pode considerar que exercícios regulares podem aumentar a taxa metabólica, enquanto uma dieta prolongada pode reduzi-la.
7.9: Uso mundial de energia
25. Qual é a diferença entre conservação de energia e lei de conservação de energia? Dê alguns exemplos de cada um.
26. Se a eficiência de uma usina de geração elétrica a carvão é de 35%, o que queremos dizer quando dizemos que a energia é uma quantidade conservada?
Problemas e exercícios
7.1: Trabalho: a definição científica
27. Quanto trabalho um atendente de supermercado faz em uma lata de sopa que ele empurra 0,600 m horizontalmente com uma força de 5,00 N? Expresse sua resposta em joules e quilocalorias.
Solução
\(\displaystyle 3.00 J=7.17×10^{−4} kcal\)
28. Uma pessoa de 75,0 kg sobe escadas, ganhando 2,50 metros de altura. Encontre o trabalho realizado para realizar essa tarefa.
29. (a) Calcule o trabalho realizado em um elevador de 1500 kg por meio de seu cabo para levantá-lo 40,0 m em velocidade constante, assumindo que a média de atrito é de 100 N.
(b) Qual é o trabalho realizado no elevador pela força gravitacional nesse processo?
(c) Qual é o trabalho total realizado no elevador?
Solução
(a)\(\displaystyle 5.92×10^5J\)
(b)\(\displaystyle −5.88×10^5J\)
(c) A força líquida é zero.
30. Suponha que um carro viaje 108 km a uma velocidade de 30,0 m/s e use 2,0 galões de gasolina. Apenas 30% da gasolina entra em trabalho útil pela força que mantém o carro em movimento em velocidade constante, apesar do atrito. (Veja [link] o conteúdo energético da gasolina.)
(a) Qual é a magnitude da força exercida para manter o carro em movimento em velocidade constante?
(b) Se a força necessária for diretamente proporcional à velocidade, quantos galões serão usados para dirigir 108 km a uma velocidade de 28,0 m/s?
31. Calcule o trabalho realizado por um homem de 85,0 kg que empurra uma caixa de 4,00 m para cima ao longo de uma rampa que faz um ângulo\(\displaystyle 20.0º\) com a horizontal. (Veja a Figura.) Ele exerce uma força de 500 N na caixa paralela à rampa e se move a uma velocidade constante. Certifique-se de incluir o trabalho que ele faz na caixa e em seu corpo para subir a rampa.
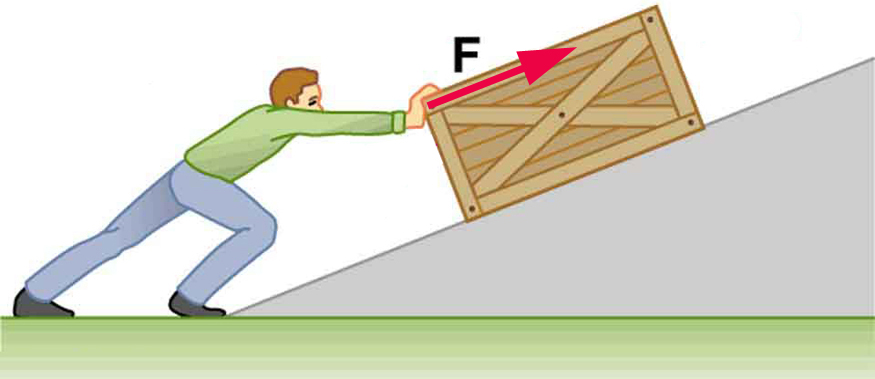
Um homem empurra uma caixa até uma rampa.
Solução
\(\displaystyle 3.14×10^3J\)
32. Quanto trabalho é feito pelo menino puxando sua irmã 30,0 m em um vagão, conforme mostrado na Figura? Suponha que nenhum atrito atue no vagão.
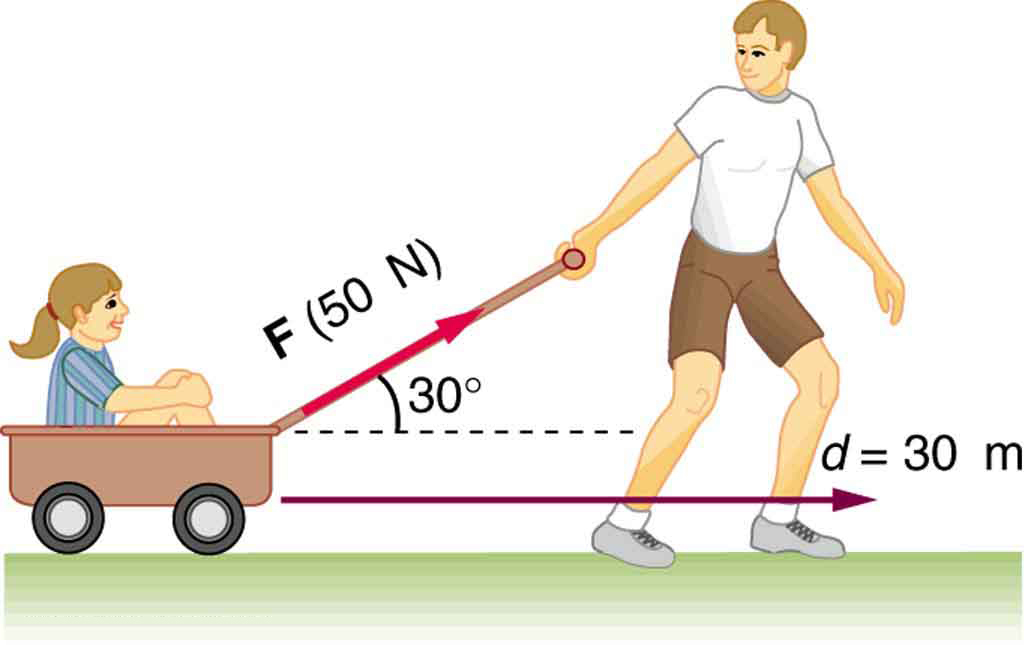
O menino trabalha no sistema do vagão e na criança quando os puxa conforme mostrado.
33. Um comprador empurra um carrinho de compras de 20,0 m em velocidade constante em terreno plano, contra uma força de atrito de 35,0 N. Ele empurra em uma direção\(\displaystyle 25.0º\) abaixo da horizontal.
(a) Qual é o trabalho realizado no carrinho por fricção?
(b) Qual é o trabalho realizado no carrinho pela força gravitacional?
(c) Qual é o trabalho realizado no carrinho pelo comprador?
(d) Encontre a força que o comprador exerce, usando considerações de energia.
(e) Qual é o trabalho total realizado no carrinho?
Solução
(a)\(\displaystyle −700J\)
(b) 0
(c) 700 J
(d) 38,6 N
(e) 0
34. Suponha que a patrulha de esqui abaixe um trenó de resgate e a vítima, com uma massa total de 90,0 kg, descendo uma\(\displaystyle 60.0º\) encosta em velocidade constante, conforme mostrado na Figura. O coeficiente de atrito entre o trenó e a neve é de 0,100.
(a) Quanto trabalho é feito por atrito quando o trenó se move 30,0 m ao longo da colina?
(b) Quanto trabalho é feito pela corda no trenó a essa distância?
(c) Qual é o trabalho realizado pela força gravitacional no trenó?
(d) Qual é o trabalho total realizado?
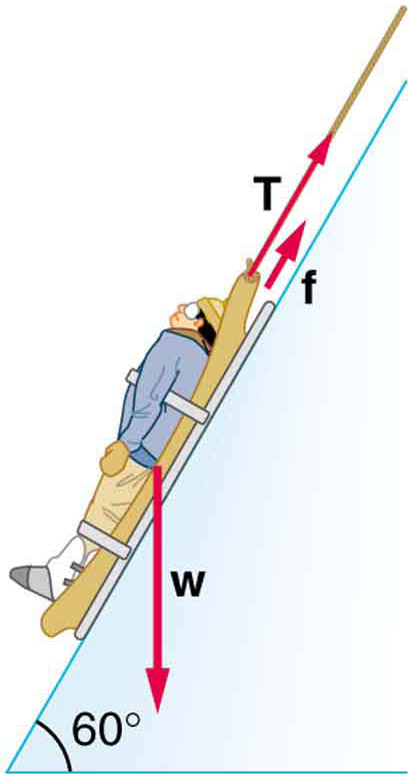
Um trenó de resgate e a vítima são abaixados em uma encosta íngreme.
7.2: Energia Cinética e o Teorema da Energia do Trabalho
35. Compare a energia cinética de um caminhão de 20.000 kg movendo-se a 110 km/h com a de um astronauta de 80,0 kg em órbita movendo-se a 27.500 km/h.
Solução
\(\displaystyle 1/250\)
36. (a) Com que rapidez um elefante de 3000 kg deve se mover para ter a mesma energia cinética de um velocista de 65,0 kg correndo a 10,0 m/s?
(b) Discuta como as maiores energias necessárias para o movimento de animais maiores se relacionariam com as taxas metabólicas.
37. Confirme o valor dado para a energia cinética de um porta-aviões em [link]. Você precisará pesquisar a definição de uma milha náutica (1 nó = 1 milha náutica/h).
Solução
\(\displaystyle 1.1×10^{10}J\)
38. (a) Calcule a força necessária para colocar um carro de 950 kg em repouso a uma velocidade de 90,0 km/h a uma distância de 120 m (uma distância bastante típica para uma parada sem pânico).
(b) Suponha que, em vez disso, o carro bata em um pilar de concreto a toda velocidade e pare em 2,00 m. Calcule a força exercida sobre o carro e compare-a com a força encontrada na parte (a).
39. O para-choque de um carro foi projetado para suportar uma colisão de 4,0 km/h (1,1 m/s) com um objeto imóvel sem danificar a carroceria do carro. O para-choque amortece o choque absorvendo a força à distância. Calcule a magnitude da força média em um para-choque que colapsa 0,200 m enquanto coloca um carro de 900 kg em repouso a partir de uma velocidade inicial de 1,1 m/s.
Solução
\(\displaystyle 2.8×10^3N\)
40. As luvas de boxe são acolchoadas para diminuir a força de um golpe.
(a) Calcule a força exercida por uma luva de boxe no rosto de um oponente, se a luva e o rosto comprimirem 7,50 cm durante um golpe no qual o braço e a luva de 7,00 kg são colocados em repouso a partir de uma velocidade inicial de 10,0 m/s.
(b) Calcule a força exercida por um golpe idêntico nos velhos tempos sangrentos, quando não eram usadas luvas e as juntas e o rosto comprimiam apenas 2,00 cm.
(c) Discuta a magnitude da força com a luva colocada. Parece alto o suficiente para causar danos, mesmo que seja menor do que a força sem luva?
41. Usando considerações de energia, calcule a força média que um velocista de 60,0 kg exerce para trás na pista para acelerar de 2,00 a 8,00 m/s em uma distância de 25,0 m, se ele encontrar um vento contrário que exerça uma força média de 30,0 N contra ele.
Solução
102 N
7.3: Energia potencial gravitacional
42. Uma usina hidrelétrica (veja a Figura) converte a energia potencial gravitacional da água atrás de uma barragem em energia elétrica.
(a) Qual é a energia potencial gravitacional em relação aos geradores de um lago de volume\(\displaystyle 50.0 km^3 (mass=5.00×10^{13}kg)\), visto que o lago tem uma altura média de 40,0 m acima dos geradores?
(b) Compare isso com a energia armazenada em uma bomba de fusão de 9 megatons.

Instalação hidrelétrica (crédito: Denis Belevich, Wikimedia Commons)
Solução
(a)\(\displaystyle 1.96×10^{16}J\)
(b) A razão entre a energia potencial gravitacional no lago e a energia armazenada na bomba é de 0,52. Ou seja, a energia armazenada no lago é aproximadamente a metade da energia de uma bomba de fusão de 9 megatons.
43. (a) Quanta energia potencial gravitacional (em relação ao solo sobre o qual foi construída) é armazenada na Grande Pirâmide de Quéops, dado que sua massa é de aproximadamente\(\displaystyle 7 × 10^9 kg\) e seu centro de massa está 36,5 m acima do solo circundante?
(b) Como essa energia se compara com a ingestão diária de alimentos de uma pessoa?
44. Suponha que um kookaburra de 350 g (um grande pássaro martim-pescador) pegue uma cobra de 75 g e a levante 2,5 m do solo até um galho.
(a) Quanto trabalho o pássaro fez na cobra?
(b) Quanto trabalho ela fez para elevar seu próprio centro de massa até o galho?
Solução
(a) 1,8 J
(b) 8,6 J
45. No exemplo, descobrimos que a velocidade de uma montanha-russa que havia descido 20,0 m era apenas um pouco maior quando tinha uma velocidade inicial de 5,00 m/s do que quando partiu do repouso. Isso implica que\(\displaystyle ΔPE >> KE_i\). Confirme esta afirmação tomando a proporção de\(\displaystyle ΔPE\) para\(\displaystyle KE_i\). (Observe que a massa é cancelada.)
46. Um carro de brinquedo de 100 g é impulsionado por uma mola comprimida que faz com que ele se mova. O carro segue a pista curva na Figura. Mostre que a velocidade final do carro de brinquedo é de 0,687 m/s se sua velocidade inicial for de 2,00 m/s e ele subir a inclinação sem atrito, ganhando 0,180 m de altitude.

Um carro de brinquedo sobe por uma pista inclinada. (crédito: Leszek Leszczynski, Flickr)
Solução
\(\displaystyle v_f=\sqrt{2gh+v_0^2}=\sqrt{2(9.80 m/s^2)(−0.180 m)+(2.00 m/s)^2}=0.687 m/s\)
47. Em uma corrida de esqui alpino, surpreendentemente, pouca vantagem é obtida ao começar a correr. (Isso ocorre porque a energia cinética inicial é pequena em comparação com o ganho de energia potencial gravitacional mesmo em pequenas colinas.) Para demonstrar isso, encontre a velocidade final e o tempo necessário para um esquiador que voa 70,0 m ao longo de uma\(\displaystyle 30º\) encosta negligenciando o atrito:
(a) Começando do descanso.
(b) Começando com uma velocidade inicial de 2,50 m/s.
(c) A resposta te surpreende? Discuta por que ainda é vantajoso começar a correr em eventos muito competitivos.
7.4: Forças conservadoras e energia potencial
48. Um trem do\(\displaystyle 5.00×10^5-kg\) metrô é parado a uma velocidade de 0,500 m/s em 0,400 m por um grande pára-choque de mola no final de sua trilha. Qual é a constante\(\displaystyle k\) de força da mola?
Solução
\(\displaystyle 7.81×10^5N/m\)
49. Um pula-pula tem uma mola com uma constante de força de\(\displaystyle 2.50×10^4N/m\), que pode ser comprimida 12,0 cm. Até que altura máxima uma criança pode pular no bastão usando apenas a energia da primavera, se a criança e o bastão tiverem uma massa total de 40,0 kg? Mostre explicitamente como você segue as etapas nas Estratégias de resolução de problemas de energia.
7.5: Forças não conservadoras
50. Um esquiador de 60,0 kg com uma velocidade inicial de 12,0 m/s sobe uma subida de 2,50 m de altura, conforme mostrado na Figura. Encontre sua velocidade final no topo, já que o coeficiente de atrito entre seus esquis e a neve é 0,0800. (Dica: encontre a distância percorrida até a inclinação assumindo um caminho em linha reta, conforme mostrado na figura.)
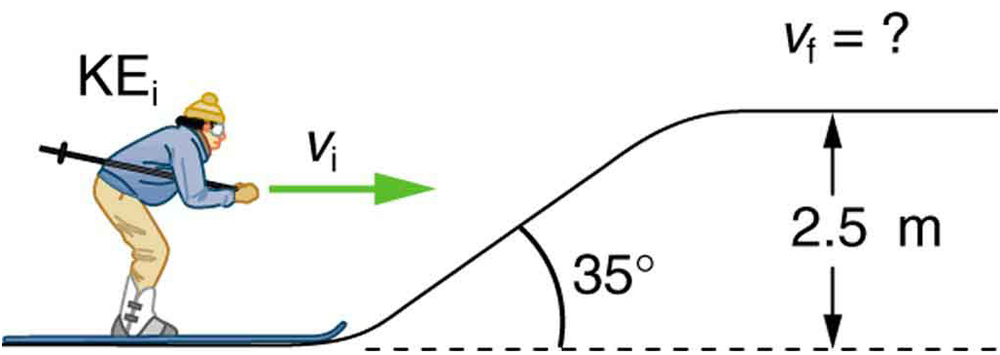
A energia cinética inicial do esquiador é parcialmente usada para descer até o topo de uma subida.
Solução
9,46 m/s
51. (a) Qual a altura de uma colina que um carro pode subir (motor desengatado) se o trabalho realizado por atrito for insignificante e sua velocidade inicial for de 110 km/h?
(b) Se, na verdade, um carro de 750 kg com uma velocidade inicial de 110 km/h for observado subindo uma colina até uma altura de 22,0 m acima de seu ponto de partida, quanta energia térmica foi gerada pelo atrito?
(c) Qual é a força média de atrito se a colina tiver uma inclinação\(\displaystyle 2.5º\) acima da horizontal?
7.6: Conservação de energia
52. Usando valores da Tabela, quantas moléculas de DNA poderiam ser quebradas pela energia transportada por um único elétron no feixe de um antigo tubo de TV? (Esses elétrons não eram perigosos em si mesmos, mas criavam raios X perigosos. Modelos posteriores de TVs de tubo tinham blindagem que absorvia os raios X antes que eles escapassem e expusessem os espectadores.)
\(\displaystyle 4×10^4\)Moléculas de solução
53. Usando considerações de energia e assumindo uma resistência insignificante ao ar, mostre que uma rocha lançada de uma ponte 20,0 m acima da água com uma velocidade inicial de 15,0 m/s atinge a água com uma velocidade de 24,8 m/s independente da direção lançada.
Solução
equacionando\(\displaystyle ΔPE_g\) e\(\displaystyle ΔKE\), obtemos\(\displaystyle v=\sqrt{2gh+v_0^2}=\sqrt{2(9.80 m/s^2)(20.0 m)+(15.0 m/s)^2}=24.8 m/s\)
54. Se a energia das bombas de fusão fosse usada para suprir as necessidades de energia do mundo, quantas da variedade de 9 megatons seriam necessárias para o suprimento de energia de um ano (usando dados da Tabela)? Isso não é tão exagerado quanto parece — existem milhares de bombas nucleares e sua energia pode ficar presa em explosões subterrâneas e convertida em eletricidade, como a energia geotérmica natural.
55. (a) O uso da fusão de hidrogênio para fornecer energia é um sonho que pode ser realizado no próximo século. A fusão seria um suprimento de energia relativamente limpo e quase ilimitado, como pode ser visto na Tabela. Para ilustrar isso, calcule por quantos anos as necessidades atuais de energia do mundo poderiam ser supridas por um milionésimo da energia de fusão de hidrogênio dos oceanos.
(b) Como esse tempo se compara a eventos historicamente significativos, como a duração de sistemas econômicos estáveis?
Solução
(a)\(\displaystyle 25×10^6years\)
(b) Isso é muito, muito mais longo do que as escalas de tempo humanas.
7.7: Potência
56. O pulsar da Nebulosa do Caranguejo (veja a Figura) é o remanescente de uma supernova que ocorreu em 1054 d.C. Usando dados da Tabela, calcule o fator aproximado pelo qual a potência desse objeto astronômico diminuiu desde sua explosão.

Nebulosa do Caranguejo (crédito: ESO, via Wikimedia Commons)
Solução
\(\displaystyle 2×10^{−10}\)
57. Suponha que uma estrela 1000 vezes mais brilhante que o nosso Sol (ou seja, emitindo 1000 vezes a potência) se torne uma supernova repentinamente. Usando dados da tabela:
(a) Por qual fator sua potência aumenta?
(b) Quantas vezes mais brilhante do que toda a nossa galáxia Via Láctea é a supernova?
(c) Com base em suas respostas, discuta se deveria ser possível observar supernovas em galáxias distantes. Observe que existem na ordem das galáxias\(\displaystyle 10^{11}\) observáveis, cujo brilho médio é um pouco menor do que a nossa própria galáxia.
58. Uma pessoa em boas condições físicas pode consumir 100 W de energia útil por várias horas seguidas, talvez pedalando um mecanismo que aciona um gerador elétrico. Negligenciando quaisquer problemas de eficiência do gerador e considerações práticas, como tempo de descanso:
(a) Quantas pessoas seriam necessárias para operar uma secadora de roupas elétrica de 4,00 kW?
(b) Quantas pessoas seriam necessárias para substituir uma grande usina elétrica que gera 800 MW?
Solução
(a) 40
(b) 8 milhões
59. Qual é o custo de operar um relógio elétrico de 3,00 W por um ano se o custo da eletricidade for de $0,0900 por\(\displaystyle kW⋅h\)?
60. Um ar condicionado doméstico grande pode consumir 15,0 kW de energia. Qual é o custo de operação deste ar condicionado 3,00 h por dia por 30,0 d se o custo da eletricidade for de $0,110 por\(\displaystyle kW⋅h\)?
Solução
$149
61. (a) Qual é o consumo médio de energia em watts de um aparelho que usa\(\displaystyle 5.00 kW⋅h\) energia por dia?
(b) Quantos joules de energia esse aparelho consome em um ano?
62. (a) Qual é a potência útil média de uma pessoa que faz\(\displaystyle 6.00×10^6J\) um trabalho útil em 8,00 h?
(b) Trabalhando nesse ritmo, quanto tempo essa pessoa levará para levantar 2000 kg de tijolos de 1,50 m até uma plataforma? (O trabalho realizado para levantar seu corpo pode ser omitido porque não é considerado um resultado útil aqui.)
Solução
(a) 208 W
(b) 141 s
63. Um dragster de 500 kg acelera do repouso até a velocidade final de 110 m/s em 400 m (cerca de um quarto de milha) e encontra uma força de atrito média de 1200 N. Qual é sua potência média em watts e potência se isso levar 7,30 s?
64. (a) Quanto tempo um carro de 850 kg com uma potência útil de 40,0 cv (1 cv = 746 W) levará para atingir uma velocidade de 15,0 m/s, negligenciando o atrito? (b) Quanto tempo essa aceleração levará se o carro também subir uma colina de 3,00 m de altura no processo?
Solução
(a) 3,20 s
(b) 4,04 s
65. (a) Encontre a potência útil de um motor de elevador que levanta uma carga de 2500 kg com uma altura de 35,0 m em 12,0 s, se também aumentar a velocidade de repouso para 4,00 m/s. Observe que a massa total do sistema contrabalançado é de 10.000 kg, de modo que apenas 2500 kg são aumentados em altura, mas os 10.000 kg completos são acelerado.
(b) Quanto custa, se a eletricidade é de $0,0900 por\(\displaystyle kW⋅h\)?
66. (a) Qual é o conteúdo de energia disponível, em joules, de uma bateria que opera um relógio elétrico de 2,00 W por 18 meses?
(b) Por quanto tempo uma bateria que pode ser fornecida\(\displaystyle 8.00×10^4J\) funciona em uma calculadora de bolso que consome energia na proporção de\(\displaystyle 1.00×10^{−3}W\)?
Solução
(a)\(\displaystyle 9.46×10^7J\)
(b)\(\displaystyle 2.54 y\)
67. (a) Quanto tempo um avião de\(\displaystyle 1.50×10^5\) -kg com motores que produzem 100 MW de potência levaria para atingir uma velocidade de 250 m/s e uma altitude de 12,0 km se a resistência do ar fosse insignificante?
(b) Se realmente levar 900 s, qual é a potência?
(c) Dada essa potência, qual é a força média de resistência do ar se o avião levar 1200 s? (Dica: você deve encontrar a distância percorrida pelo avião em 1200 s, assumindo uma aceleração constante.)
68. Calcule a potência necessária para que um carro de 950 kg suba uma\(\displaystyle 2.00º\) inclinação a uma temperatura constante de 30,0 m/s enquanto encontra resistência ao vento e atrito totalizando 600 N. Mostre explicitamente como você segue as etapas nas Estratégias de Solução de Problemas de Energia.
Solução
Identifique conhecidos:\(\displaystyle m=950 kg\), ângulo de inclinação\(\displaystyle θ=2.00º, v=3.00 m/s, f=600 N\)
Identifique incógnitas: potência\(\displaystyle P\) do carro, força\(\displaystyle F\) que o carro aplica à estrada
Resolva para desconhecido:
\(\displaystyle P=\frac{W}{t}=\frac{Fd}{t}=F(\frac{d}{t})=Fv,\)
onde \(\displaystyle F\)é paralelo à inclinação e deve se opor às forças resistivas e à força da gravidade:
\(\displaystyle F=f+w=600 N+mgsinθ\)
Insira isso na expressão de potência e resolva:
\(\displaystyle P=(f+mgsinθ)v\)
\(\displaystyle =[600 N+(950 kg)(9.80 m/s^2)sin 2º](30.0 m/s)\)
\(\displaystyle =2.77×10^4W\)
Cerca de 28 kW (ou cerca de 37 cv) é razoável para um carro subir uma inclinação suave.
69. (a) Calcule a potência por metro quadrado que atinge a alta atmosfera da Terra a partir do Sol. (Considere a potência de saída do Sol em ser\(\displaystyle 4.00×10^{26}W\).)
(b) Parte disso é absorvida e refletida pela atmosfera, de modo que um máximo de\(\displaystyle 1.30 kW/m^2\) atinge a superfície da Terra. Calcule a área\(\displaystyle km^2\) de coletores de energia solar necessária para substituir uma usina elétrica que gera 750 MW se os coletores converterem uma média de 2,00% da potência máxima em eletricidade. (Essa pequena eficiência de conversão se deve aos próprios dispositivos e ao fato de o sol estar diretamente acima apenas brevemente.) Com as mesmas suposições, qual área seria necessária para atender às necessidades de energia dos Estados Unidos\(\displaystyle (1.05×10^{20}J)\)? As necessidades de energia da Austrália\(\displaystyle (5.4×10^{18}J)\)? As necessidades energéticas da China\(\displaystyle (6.3×10^{19}J)\)? (Esses valores de consumo de energia são de 2006.)
7.8: Trabalho, energia e poder em humanos
70. (a) Por quanto tempo você consegue subir escadas rapidamente (116/min) com 93,0 kcal de energia em um pedaço de manteiga de 10,0 g?
(b) Quantos voos são esses se cada voo tiver 16 escadas?
Solução
(a) 9,5 min
(b) 69 lances de escada
71. (a) Qual é a potência em watts e potência de um velocista de 70,0 kg que acelera do repouso até 10,0 m/s em 3,00 s?
(b) Considerando a quantidade de energia gerada, você acha que um atleta bem treinado poderia fazer isso repetidamente por longos períodos de tempo?
72. Calcule a potência em watts e potência de um arremessador que leva 1,20 s para acelerar o disparo de 7,27 kg do repouso para 14,0 m/s, enquanto o eleva para 0,800 m. (Não inclua a potência produzida para acelerar seu corpo).

Tiro de arremesso no Dornoch Highland Gathering em 2007. (crédito: John Haslam, Flickr)
Solução
641 W, 0,860 hp
73. (a) Qual é a eficiência de um professor fora\(\displaystyle 2.10×10^5 J\) de condição que faz um trabalho útil enquanto metaboliza 500 kcal de energia alimentar?
(b) Quantas calorias alimentares um atleta bem condicionado metabolizaria ao fazer o mesmo trabalho com uma eficiência de 20%?
74. A energia que não é utilizada para trabalho ou transferência de calor é convertida na energia química da gordura corporal contendo cerca de 39 kJ/g. Quantos gramas de gordura você ganhará se comer 10.000 kJ (cerca de 2500 kcal) um dia e não fizer nada além de ficar relaxado por 16,0 h e dormir por outras 8,00 h? Use os dados da Tabela para as taxas de consumo de energia dessas atividades.
Solução
31 g
75. Usando os dados da Tabela, calcule as necessidades diárias de energia de uma pessoa que dorme por 7,00 h, caminha por 2,00 h, frequenta as aulas por 4,00 h, pedala por 2,00 h, fica relaxada por 3,00 h e estuda por 6,00 h. (Estudar consome energia na mesma proporção que está sentado na sala de aula).
76. Qual é a eficiência de um sujeito em uma esteira que trabalha na taxa de 100 W enquanto consome oxigênio na taxa de 2,00 L/min? (Dica: Veja a tabela.)
Solução
14,3%
77. Retirar a neve pode ser extremamente desgastante porque as armas têm uma eficiência muito baixa nessa atividade. Suponha que uma pessoa cavando uma trilha metabolize os alimentos a uma taxa de 800 W.
(a) Qual é a potência útil dela?
(b) Quanto tempo ela levará para levantar 3000 kg de neve de 1,20 m? (Essa pode ser a quantidade de neve pesada em 20 m de trilha.)
(c) Quanto desperdício de transferência de calor em quilojoules ela gerará no processo?
78. Forças muito grandes são produzidas nas juntas quando uma pessoa pula de alguma altura para o chão.
(a) Calcule a magnitude da força produzida se uma pessoa de 80,0 kg pular de uma saliência de 0,600 m de altura e pousar rigidamente, comprimindo o material da junta de 1,50 cm como resultado. (Certifique-se de incluir o peso da pessoa.)
(b) Na prática, os joelhos se dobram quase involuntariamente para ajudar a aumentar a distância pela qual você para. Calcule a magnitude da força produzida se a distância de parada for de 0,300 m.
(c) Compare as duas forças com o peso da pessoa.
Solução
(a)\(\displaystyle 3.21×10^4 N\)
(b)\(\displaystyle 2.35×10^3 N\)
(c) A relação entre a força líquida e o peso da pessoa é de 41,0 na parte (a); 3,00 na parte (b)
79. Correr em superfícies duras com sapatos insuficientemente acolchoados produz grandes forças nos pés e nas pernas.
(a) Calcule a magnitude da força necessária para interromper o movimento descendente da perna de um corredor, se sua perna tiver uma massa de 13,0 kg, uma velocidade de 6,00 m/s e parar a uma distância de 1,50 cm. (Certifique-se de incluir o peso do corpo do corredor de 75,0 kg.)
(b) Compare essa força com o peso do corredor.
80. (a) Calcule a energia em kJ usada por uma mulher de 55,0 kg que faz 50 curvas profundas do joelho nas quais seu centro de massa é abaixado e elevado em 0,400 m. (Ela trabalha em ambas as direções). Você pode presumir que a eficiência dela é de 20%.
(b) Qual é a taxa média de consumo de energia em watts se ela fizer isso em 3,00 min?
Solução
(a) 108 kJ
(b) 59 W
81. Kanellos Kanellopoulos voou 119 km de Creta para Santorini, Grécia, em 23 de abril de 1988, no Daedalus 88, uma aeronave movida por um mecanismo de acionamento do tipo bicicleta (veja a Figura). Sua potência útil para a viagem de 234 minutos foi de cerca de 350 W. Usando a eficiência para pedalar de [link], calcule a energia alimentar em quilojoules que ele metabolizou durante o voo.

O Daedalus 88 em voo. (crédito: foto da NASA de Beasley)
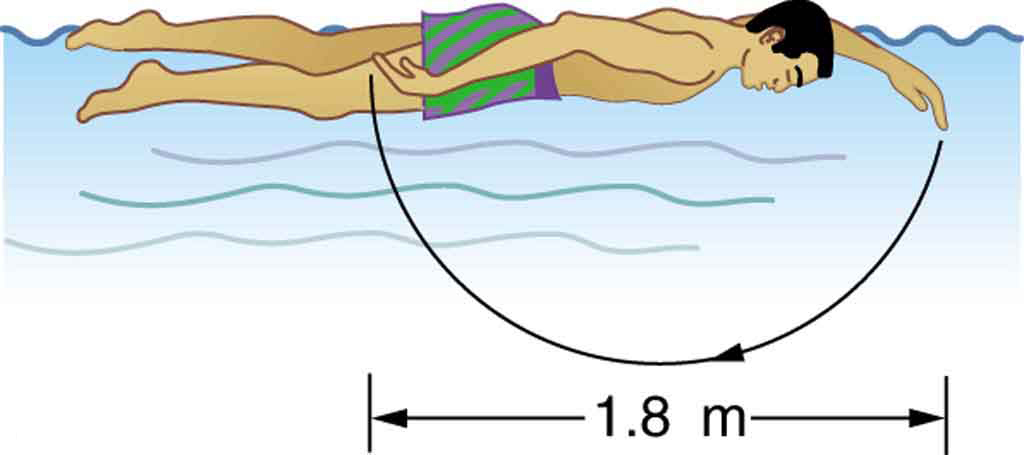
82. O nadador mostrado na Figura exerce uma força horizontal média para trás de 80,0 N com o braço durante cada traçado de 1,80 m de comprimento.
(a) Qual é a sua produção de trabalho em cada acidente vascular cerebral?
(b) Calcule a potência de seus braços se ele fizer 120 golpes por minuto.
Solução
(a) 144 J
(b) 288 W
83. Os alpinistas transportam oxigênio engarrafado quando estão em altitudes muito altas.
(a) Supondo que um alpinista use oxigênio duas vezes a taxa para subir 116 escadas por minuto (devido à baixa temperatura do ar e aos ventos), calcule quantos litros de oxigênio um alpinista precisaria para 10,0 h de escalada. (São litros ao nível do mar.) Observe que apenas 40% do oxigênio inalado é utilizado; o restante é exalado.
(b) Quanto trabalho útil o alpinista faz se ele e seu equipamento tiverem uma massa de 90,0 kg e ele ganharem 1000 m de altitude?
(c) Qual é a eficiência dele para a subida de 10,0 h?
84. A imponente Grande Pirâmide de Quéops foi construída há mais de 4500 anos. Sua base quadrada, originalmente 230 m de lado, cobria 13,1 acres e tinha 146 m de altura, com uma massa de cerca de\(\displaystyle 7×10^9kg\). (As dimensões da pirâmide são ligeiramente diferentes hoje devido à extração e a alguma flacidez.) Os historiadores estimam que 20.000 trabalhadores gastaram 20 anos para construí-lo, trabalhando 12 horas por dia, 330 dias por ano.
(a) Calcule a energia potencial gravitacional armazenada na pirâmide, dado que seu centro de massa está a um quarto de sua altura.
(b) Apenas uma fração dos trabalhadores levantou blocos; a maioria estava envolvida em serviços de apoio, como construir rampas (ver Figura), levar comida e água e transportar blocos para o local. Calcule a eficiência dos trabalhadores que fizeram o levantamento, assumindo que havia 1000 deles e consumiam energia alimentar à taxa de 300 kcal/h. O que sua resposta implica sobre quanto de seu trabalho foi dedicado ao levantamento de blocos, versus quanto trabalho foi feito para atrito e levantamento e abaixamento de seus próprios corpos ?
(c) Calcule a massa de comida que deveria ser fornecida todos os dias, assumindo que o trabalhador médio necessitava de 3600 kcal por dia e que sua dieta era de 5% de proteína, 60% de carboidratos e 35% de gordura. (Essas proporções negligenciam a massa de materiais a granel e não digeríveis consumidos.)
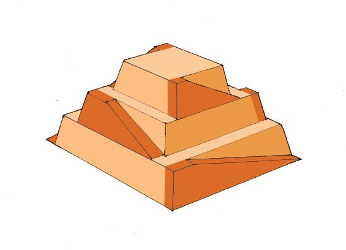
As pirâmides antigas provavelmente foram construídas usando rampas como máquinas simples. (crédito: Franck Monnier, Wikimedia Commons)
Solução
(a)\(\displaystyle 2.50×10^{12} J\)
(b) 2,52%
(c)\(\displaystyle 1.4×10^4 kg\) (14 toneladas métricas)
85. (a) Por quanto tempo você pode jogar tênis com os 800 kJ (cerca de 200 kcal) de energia em uma barra de chocolate?
(b) Isso parece muito tempo? Discuta por que o exercício é necessário, mas pode não ser suficiente para fazer com que a pessoa perca peso.
7.9: Uso mundial de energia
86. Conceitos integrados
(a) Calcule a força que a mulher na Figura exerce para fazer uma flexão em velocidade constante, levando todos os dados a serem conhecidos em três dígitos.
(b) Quanto trabalho ela faz se seu centro de massa subir 0,240 m?
(c) Qual é a potência útil dela se ela fizer 25 flexões em 1 min? (O trabalho realizado para abaixar seu corpo deve ser incluído? Veja a discussão sobre trabalhos úteis em Trabalho, Energia e Poder em Humanos.
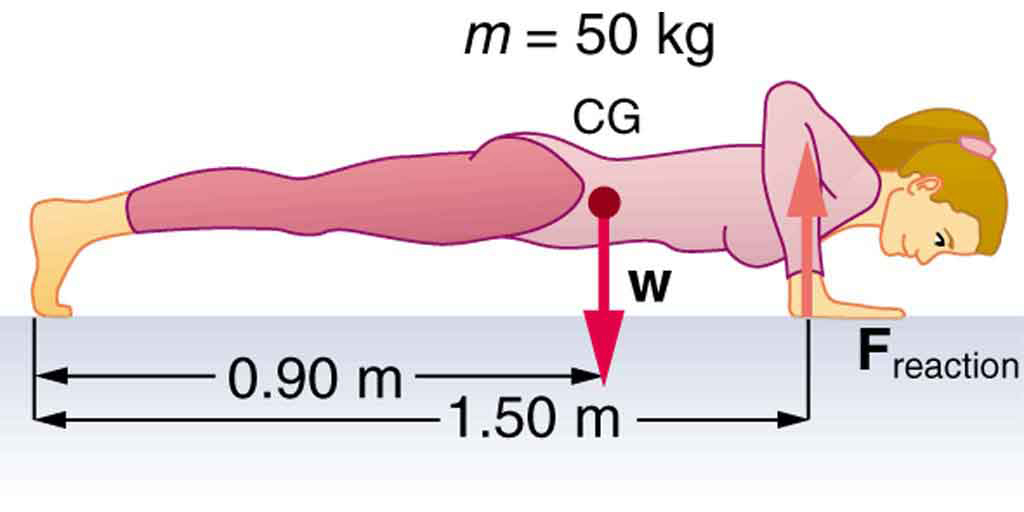
Forças envolvidas em fazer flexões. O peso da mulher age como uma força exercida para baixo em seu centro de gravidade (CG).
Solução
(a) 294 N
(b) 118 J
(c) 49,0 W
87. Conceitos integrados
Um esquiador cross-country de 75,0 kg está subindo uma\(\displaystyle 3.0º\) encosta a uma velocidade constante de 2,00 m/s e encontra resistência do ar de 25,0 N. Encontre sua potência para o trabalho realizado contra a força gravitacional e a resistência do ar.
(b) Que força média ele exerce para trás na neve para fazer isso?
(c) Se ele continuar exercendo essa força e a experimentar a mesma resistência do ar ao atingir uma área nivelada, quanto tempo ele levará para atingir uma velocidade de 10,0 m/s?
88. Conceitos integrados
O nadador de 70,0 kg em [link] inicia uma corrida com uma velocidade inicial de 1,25 m/s e exerce uma força média de 80,0 N para trás com os braços durante cada traçado de 1,80 m de comprimento.
(a) Qual é a aceleração inicial dele se a resistência à água for de 45,0 N?
(b) Qual é a força média de resistência subsequente da água durante os 5,00 s que ele leva para atingir sua velocidade máxima de 2,50 m/s?
(c) Discuta se a resistência à água parece aumentar linearmente com a velocidade.
Solução
(a)\(\displaystyle 0.500 m/s^2\)
(b)\(\displaystyle 62.5 N\)
(c) Supondo que a aceleração do nadador diminua linearmente com o tempo no intervalo de 5,00 s, a força de atrito deve, portanto, aumentar linearmente com o tempo, pois\(\displaystyle f=F−ma\). Se a aceleração diminuir linearmente com o tempo, a velocidade conterá um termo dependente do tempo ao quadrado (\(\displaystyle t^2\)). Portanto, a resistência à água não dependerá linearmente da velocidade.
89. Conceitos integrados
Uma pistola de brinquedo usa uma mola com uma força constante de 300 N/m para impulsionar uma esfera de aço de 10,0 g. Se a mola for comprimida 7,00 cm e o atrito for insignificante:
(a) Quanta força é necessária para comprimir a mola?
(b) Até que altura máxima a bola pode ser arremessada?
(c) Em que ângulos acima da horizontal uma criança pode tentar atingir um alvo a 3,00 m de distância na mesma altura da arma?
(d) Qual é o alcance máximo da arma em terreno nivelado?
90. Conceitos integrados
(a) Que força deve ser fornecida por um cabo de elevador para produzir uma aceleração\(\displaystyle 0.800 m/s^2\) contra uma força de atrito de 200 N, se a massa do elevador carregado for de 1500 kg?
(b) Quanto trabalho é feito pelo cabo na elevação do elevador de 20,0 m?
(c) Qual é a velocidade final do elevador se ele partir do repouso?
(d) Quanto trabalho foi gasto em energia térmica?
Solução
(a)\(\displaystyle 16.1×10^3N\)
(b)\(\displaystyle 3.22×10^5J\)
(c)\(\displaystyle 5.66 m/s\)
(d) 4,0 kJ
91. Resultados irracionais
Um anúncio de carro afirma que seu carro de 900 kg acelerou do repouso para 30,0 m/s e dirigiu 100 km, ganhando 3,00 km de altitude, com 1,0 galão de gasolina. A força média de atrito, incluindo a resistência do ar, foi de 700 N. Suponha que todos os valores sejam conhecidos por três números significativos.
(a) Calcule a eficiência do carro.
(b) O que não é razoável no resultado?
(c) Quais premissas não são razoáveis ou quais são inconsistentes?
92. Resultados irracionais
A gordura corporal é metabolizada, fornecendo 9,30 kcal/g, quando a ingestão alimentar é menor do que a necessária para estimular o metabolismo. Os fabricantes de uma bicicleta ergométrica afirmam que você pode perder 0,500 kg de gordura por dia se exercitando vigorosamente por 2,00 h por dia em sua máquina.
(a) Quantos kcal são fornecidos pela metabolização de 0,500 kg de gordura?
(b) Calcule o kcal/min que você teria que utilizar para metabolizar a gordura na taxa de 0,500 kg em 2,00 h.
(c) O que não é razoável nos resultados?
(d) Quais premissas não são razoáveis ou quais premissas são inconsistentes?
Solução
(a)\(\displaystyle 4.65×10^3kcal\)
(b) 38,8 kcal/min
(c) Essa potência de saída é superior ao valor mais alto em [link], que é de cerca de 35 kcal/min (correspondendo a 2415 watts) para corrida.
(d) Seria impossível manter essa potência por 2 horas (imagine correr por 2 horas!).
93. Construa seu próprio problema
Considere uma pessoa subindo e descendo escadas. Construa um problema no qual você calcule a taxa de longo prazo na qual as escadas podem ser escaladas considerando a massa da pessoa, sua capacidade de gerar energia com as pernas e a altura de um único degrau. Considere também por que a mesma pessoa pode descer escadas em um ritmo mais rápido por um tempo quase ilimitado, apesar do fato de que forças muito semelhantes são exercidas descendo e subindo. (Isso aponta para um processo fundamentalmente diferente de descer e subir escadas.)
94. Construa seu próprio problema
Considere os humanos gerando eletricidade pedalando um dispositivo semelhante a uma bicicleta ergométrica. Crie um problema no qual você determine o número de pessoas necessárias para substituir uma grande instalação de geração elétrica. Entre as coisas a considerar estão a potência que é razoável usando as pernas, o tempo de descanso e a necessidade de eletricidade 24 horas por dia. Discuta as implicações práticas de seus resultados.
95. Conceitos integrados
Um jogador de basquete de 105 kg se agacha 0,400 m enquanto espera para pular. Depois de exercer uma força no chão através desses 0,400 m, seus pés saem do chão e seu centro de gravidade sobe 0,950 m acima de sua posição ereta normal.
(a) Usando considerações de energia, calcule sua velocidade quando ele sair do chão.
(b) Que força média ele exerceu no chão? (Não negligencie a força para suportar seu peso, bem como a força para acelerá-lo.)
(c) Qual foi sua potência durante a fase de aceleração?
Solução
(a) 4,32 m/s
(b)\(\displaystyle 3.47×10^3N\)
(c) 8,93 kW

