4.E: Dinâmica - Força e Leis do Movimento de Newton (Exercícios)
- Page ID
- 194753
Perguntas conceituais
4.1: Desenvolvimento do conceito de força
1. Proponha um padrão de força diferente do exemplo de uma mola esticada discutido no texto. Seu padrão deve ser capaz de produzir a mesma força repetidamente.
2. Quais propriedades as forças têm que nos permitem classificá-las como vetores?
4.2: Primeira Lei do Movimento de Newton: Inércia
3. Como a inércia e a massa estão relacionadas?
4. Qual é a relação entre peso e massa? Qual é uma propriedade intrínseca e imutável de um corpo?
4.3: Segunda Lei do Movimento de Newton: Conceito de um Sistema
5. Qual afirmação está correta? Explique sua resposta e dê um exemplo.
(a) A força líquida causa movimento.
(b) A força líquida causa mudança no movimento.
6. Por que podemos negligenciar forças como as que mantêm um corpo unido quando aplicamos a segunda lei do movimento de Newton?
7. Explique como a escolha do “sistema de interesse” afeta quais forças devem ser consideradas ao aplicar a segunda lei do movimento de Newton.
8. Descreva uma situação na qual a força externa líquida em um sistema não é zero, mas sua velocidade permanece constante.
9. o sistema pode ter uma velocidade diferente de zero, enquanto a força externa líquida sobre ele é zero. Descreva essa situação.
10. Uma pedra é jogada diretamente para cima. Qual é a força externa líquida atuando na rocha quando ela está no topo de sua trajetória?
11. (a) Dê um exemplo de diferentes forças externas líquidas atuando no mesmo sistema para produzir acelerações diferentes.
(b) Dê um exemplo da mesma força externa líquida atuando em sistemas de massas diferentes, produzindo diferentes acelerações.
(c) Qual lei descreve com precisão os dois efeitos? Declare isso em palavras e como uma equação.
12. Se a aceleração de um sistema for zero, não há forças externas atuando sobre ele? E quanto às forças internas? Explique suas respostas.
13. Se uma força constante, diferente de zero, for aplicada a um objeto, o que você pode dizer sobre a velocidade e a aceleração do objeto?
14. A força gravitacional na bola de basquete na Figura é ignorada. Quando a gravidade é levada em consideração, qual é a direção da força externa líquida na bola de basquete — acima da horizontal, abaixo da horizontal ou ainda na horizontal?
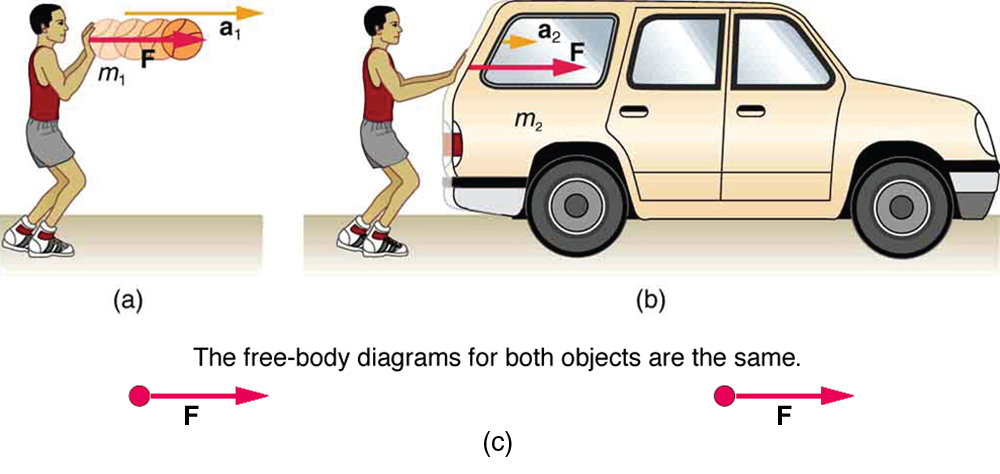
4.4: Terceira Lei do Movimento de Newton: Simetria nas Forças
15. Quando você decola em um avião a jato, há a sensação de ser empurrado de volta para o assento. Explique por que você se move para trás no assento — há realmente uma força para trás em você? (O mesmo raciocínio explica lesões cervicais, nas quais a cabeça aparentemente é jogada para trás.)
16. Um dispositivo usado desde a década de 1940 para medir o chute ou o recuo do corpo devido aos batimentos cardíacos é o “balistocardiógrafo”. Quais princípios físicos estão envolvidos aqui para medir a força da contração cardíaca? Como podemos construir um dispositivo desse tipo?
17. Descreva uma situação em que um sistema exerce uma força sobre outro e, como consequência, experimenta uma força que é igual em magnitude e direção oposta. Quais das leis do movimento de Newton se aplicam?
18. Por que um rifle comum recua (chuta para trás) quando é disparado? O cano de um rifle sem recuo está aberto nas duas extremidades. Descreva como a terceira lei de Newton se aplica quando alguém é demitido. Você pode ficar perto de um deles com segurança quando ele é disparado?
19. Um atacante de futebol americano argumenta que não faz sentido tentar superar o jogador adversário, pois não importa o quanto ele empurre, ele experimentará uma força igual e oposta à do outro jogador. Use as leis de Newton e desenhe um diagrama de corpo livre de um sistema apropriado para explicar como ele ainda pode superar a oposição se for forte o suficiente.
20. A terceira lei do movimento de Newton nos diz que as forças sempre ocorrem em pares de magnitude igual e oposta. Explique como a escolha do “sistema de interesse” afeta o cancelamento de um desses pares de forças.
4.5: Normal, tensão e outros exemplos de forças
21. Se uma perna for suspensa por uma configuração de tração, conforme mostrado na Figura, qual é a tensão na corda?
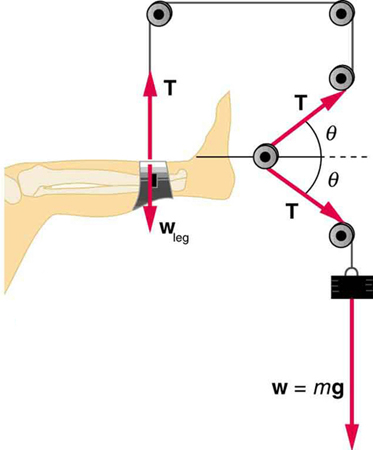
Uma perna é suspensa por um sistema de tração no qual os fios são usados para transmitir forças. Polias sem atrito mudam a direção da força\(\displaystyle T\) sem alterar sua magnitude.
22. Em uma configuração de tração para um osso quebrado, com polias e cordas disponíveis, como podemos aumentar a força ao longo da tíbia usando o mesmo peso? (Veja a Figura.) (Observe que a tíbia é a tíbia mostrada nesta imagem.)
4.7: Outras aplicações das Leis do Movimento de Newton
23. Para simular a aparente ausência de peso da órbita espacial, os astronautas são treinados no porão de uma aeronave de carga que está acelerando para baixo em\(\displaystyle g\). Por que eles parecerão leves, medidos ao se posicionar em uma balança de banheiro, nesse quadro de referência acelerado? Existe alguma diferença entre sua aparente ausência de peso em órbita e na aeronave?
24. Um desenho animado mostra a peruca saindo da cabeça de um passageiro do elevador quando o elevador para rapidamente durante uma subida. Isso pode realmente acontecer sem que a pessoa esteja amarrada ao chão do elevador? Explique sua resposta.
4.8: Tópico estendido: As quatro forças básicas — uma introdução
25. Explique, em termos das propriedades das quatro forças básicas, por que as pessoas notam a força gravitacional atuando em seus corpos se for uma força comparativamente fraca.
26. Qual é a força dominante entre objetos astronômicos? Por que as outras três forças básicas são menos significativas nessas distâncias muito grandes?
27. Dê um exemplo detalhado de como a troca de uma partícula pode resultar em uma força atrativa. (Por exemplo, considere uma criança tirar um brinquedo das mãos de outra.)
Problemas e exercícios
4.3: Segunda Lei do Movimento de Newton: Conceito de um Sistema
Você pode presumir que os dados retirados das ilustrações têm precisão de três dígitos.
28. Um velocista de 63,0 kg inicia uma corrida com uma aceleração de\(\displaystyle 4.20 m/s^2\). Qual é a força externa líquida sobre ele?
Solução
265 N
29. Se o velocista do problema anterior acelerar nessa velocidade por 20 m e depois manter essa velocidade pelo restante da corrida de 100 m, qual será seu tempo para a corrida?
30. Um limpador empurra um carrinho de roupa suja de 4,50 kg de tal forma que a força externa líquida sobre ele seja de 60,0 N. Calcule a magnitude de sua aceleração.
Solução
\(\displaystyle 13.3 m/s^2\)
31. Como os astronautas em órbita aparentemente não têm peso, é necessário um método inteligente de medir suas massas para monitorar seus ganhos ou perdas de massa e ajustar as dietas. Uma forma de fazer isso é exercer uma força conhecida sobre um astronauta e medir a aceleração produzida. Suponha que uma força externa líquida de 50,0 N seja exercida e a aceleração do astronauta seja medida como sendo\(\displaystyle 0.893 m/s^2\).
(a) Calcule sua massa.
(b) Ao exercer uma força sobre o astronauta, o veículo no qual eles orbitam experimenta uma força igual e oposta. Discuta como isso afetaria a medição da aceleração do astronauta. Proponha um método no qual o recuo do veículo seja evitado.
32. Na Figura 4.4.3, a força externa líquida no cortador de grama de 24 kg é declarada em 51 N. Se a força de atrito oposta ao movimento for 24 N, que força\(\displaystyle F\) (em newtons) a pessoa está exercendo sobre o cortador? Suponha que o cortador esteja se movendo a 1,5 m/s quando a força\(\displaystyle F\) for removida. Até onde o cortador irá antes de parar?
Solução
1,1 m
33. O mesmo trenó de foguete desenhado na Figura é desacelerado a uma taxa de\(\displaystyle 196 m/s^2\). Que força é necessária para produzir essa desaceleração? Suponha que os foguetes estejam desligados. A massa do sistema é de 2100 kg.
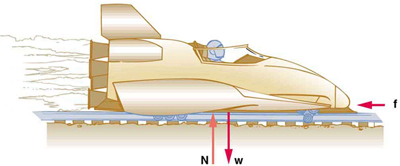
34. (a) Se o foguete mostrado na Figura começar com apenas um foguete queimando, qual é a magnitude de sua aceleração? Suponha que a massa do sistema seja de 2100 kg, o empuxo T seja\(\displaystyle 2.4×10^4\) N e que a força de atrito que se opõe ao movimento seja conhecida como 650 N.
(b) Por que a aceleração não é um quarto do que é com todos os foguetes queimando?
Solução
(a)\(\displaystyle 11m/s^2\)
(b) A aceleração não é um quarto do que era com todos os foguetes queimando porque a força de atrito ainda é tão grande quanto era com todos os foguetes queimando.
35. Qual é a desaceleração do foguete se ele parar em 1,1 s a partir de uma velocidade de 1000 km/h? (Essa desaceleração fez com que um sujeito do teste desmaiasse e tivesse cegueira temporária.)
36. Suponha que duas crianças empurrem horizontalmente, mas em direções exatamente opostas, uma terceira criança em um vagão. O primeiro filho exerce uma força de 75,0 N, o segundo uma força de 90,0 N, o atrito é 12,0 N e a massa do terceiro filho mais o vagão é de 23,0 kg.
(a) Qual é o sistema de interesse se a aceleração da criança no vagão for calculada?
(b) Desenhe um diagrama de corpo livre, incluindo todas as forças que atuam no sistema.
(c) Calcule a aceleração.
(d) Qual seria a aceleração se o atrito fosse 15,0 N?
Solução
(a) O sistema é a criança no vagão mais o vagão.
(b)
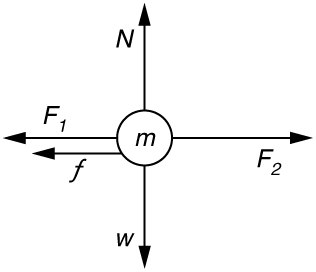
(c)\(\displaystyle a=0.130m/s^2\) na direção do impulso da segunda criança.
(d)\(\displaystyle a=0.00m/s^2\)
37. Uma motocicleta potente pode produzir uma aceleração de\(\displaystyle 3.50m/s^2\) ao viajar a 90,0 km/h. Nessa velocidade, as forças que resistem ao movimento, incluindo atrito e resistência ao ar, totalizam 400 N. (A resistência do ar é análoga ao atrito aéreo). Ela sempre se opõe ao movimento de um objeto.) Qual é a magnitude da força que a motocicleta exerce para trás no solo para produzir sua aceleração se a massa da motocicleta com piloto for de 245 kg?
38. O trenó de foguete mostrado na Figura acelera a uma taxa de\(\displaystyle 49.0m/s^2\). Seu passageiro tem uma massa de 75,0 kg.
(a) Calcule o componente horizontal da força que o assento exerce contra seu corpo. Compare isso com o peso dele usando uma proporção.
(b) Calcule a direção e a magnitude da força total que o assento exerce contra seu corpo.
Solução
(a)\(\displaystyle 3.68×10^3N\). Essa força é 5,00 vezes maior do que seu peso.
(b)\(\displaystyle 3750 N; 11.3ºabove horizontal\)

39. Repita o problema anterior para a situação em que o trenó do foguete desacelera a uma taxa de\(\displaystyle 201 m/s^2\). Nesse problema, as forças são exercidas pelo assento e pelos cintos de retenção.
40. O peso de um astronauta mais seu traje espacial na Lua é de apenas 250 N. Quanto eles pesam na Terra? Qual é a massa na Lua? Na Terra?
Solução
\(\displaystyle 1.5×10^3N,150 kg,150 kg\)
41. Suponha que a massa de um módulo totalmente carregado no qual os astronautas decolam da Lua seja de 10.000 kg. O empuxo de seus motores é de 30.000 N. (a) Calcule a magnitude da aceleração em uma decolagem vertical da Lua. (b) Poderia decolar da Terra? Se não, por que não? Se possível, calcule a magnitude de sua aceleração.
4.4: Terceira Lei do Movimento de Newton: Simetria nas Forças
42. Que força externa líquida é exercida em um projétil de artilharia de 1100 kg disparado de um navio de guerra se o projétil for acelerado a\(\displaystyle 2.40×10^4m/s^2\)? Qual é a magnitude da força exercida no navio pelo projétil de artilharia?
Força de solução no projétil:\(\displaystyle 2.64×10^7N\)
Força exercida no navio =\(\displaystyle −2.64×10^7N\), pela terceira lei de Newton
43. Um jogador de rúgbi corajoso, mas inadequado, está sendo empurrado para trás por um jogador adversário que está exercendo uma força de 800 N sobre ele. A massa do jogador perdedor mais o equipamento é de 90,0 kg, e ele está acelerando a 1,20 m/s2 tamanho 12 {1 “.” “20"” m/s” RSup {tamanho 8 {2}}} {} para trás. (a) Qual é a força de atrito entre os pés do jogador perdedor e a grama? (b) Que força o jogador vencedor exerce no chão para avançar se sua massa mais equipamento for de 110 kg? (c) Faça um esboço da situação mostrando o sistema de interesse usado para resolver cada parte. Para essa situação, desenhe um diagrama de corpo livre e escreva a equação da força líquida.
4.5: Normal, tensão e outros exemplos de forças
44. Duas equipes de nove membros se envolvem em um cabo de guerra. Cada um dos membros da primeira equipe tem uma massa média de 68 kg e exerce uma força média de 1350 N horizontalmente. Cada um dos membros da segunda equipe tem uma massa média de 73 kg e exerce uma força média de 1365 N horizontalmente.
(a) Qual é a magnitude da aceleração das duas equipes?
(b) Qual é a tensão na seção de corda entre as equipes?
Solução
a.\(\displaystyle 0.11 m/s^2\)
b.\(\displaystyle 1.2×10^4N\)
45. Que força um trampolim precisa aplicar a uma ginasta de 45,0 kg para acelerá-la em linha reta\(\displaystyle 7.50 m/s^2\)? Observe que a resposta é independente da velocidade da ginasta — ela pode estar se movendo para cima ou para baixo ou ficar parada.
46. (a) Calcule a tensão em um fio vertical de teia de aranha se uma aranha de massa\(\displaystyle 8.00×10^{−5}kg\) ficar imóvel sobre ele.
(b) Calcule a tensão em um fio horizontal de teia de aranha se a mesma aranha ficar imóvel no meio dela, como o equilibrista da Figura. O fio cede em um ângulo\(\displaystyle 12º\) abaixo da horizontal. Compare isso com a tensão na corda vertical (encontre sua proporção).
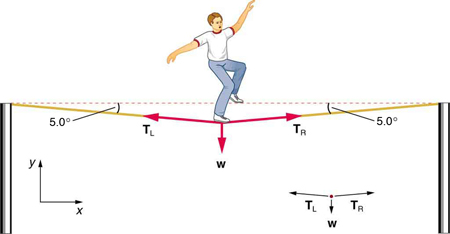
Solução
(a)\(\displaystyle 7.84×10^{-4}N\)
(b)\(\displaystyle 1.89×10^{–3}N\). Isso é 2,41 vezes a tensão na corda vertical.
47. Suponha que um ginasta de 60,0 kg suba em uma corda.
(a) Qual é a tensão na corda se ele subir a uma velocidade constante?
(b) Qual é a tensão na corda se ele acelera para cima a uma taxa de\(\displaystyle 1.50 m/s^2\)?
48. Mostre que, conforme declarado no texto, uma força\(\displaystyle F_{⊥}\) exercida sobre um meio flexível em seu centro e perpendicular ao seu comprimento (como no fio da corda bamba na Figura) dá origem a uma tensão de magnitude\(\displaystyle T=\frac{F_⊥}{2sin(θ)}\).
Solução A segunda lei de
Newton aplicada na direção vertical fornece
\(\displaystyle F_y=F−2Tsinθ=0\)
\(\displaystyle F=2Tsinθ\)
\(\displaystyle T=\frac{F}{2 sinθ}\).
49. Considere o bebê sendo pesado na Figura.
(a) Qual é a massa da criança e da cesta se uma leitura da escala de 55 N for observada?
(b) Qual é a tensão\(\displaystyle T_1\) no cordão que prende o bebê à balança?
(c) Qual é a tensão\(\displaystyle T_2\) no cabo que liga a balança ao teto, se a balança tiver uma massa de 0,500 kg?
(d) Desenhe um esboço da situação indicando o sistema de interesse usado para resolver cada parte. As massas dos cabos são insignificantes.
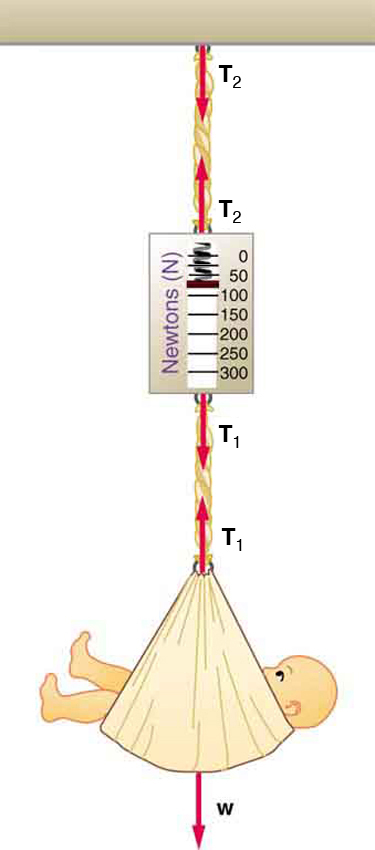
Um bebê é pesado usando uma balança de mola.
4.6: Estratégias de resolução de problemas
50. Um\(\displaystyle 5.00×10^5-kg\) foguete está acelerando em linha reta. Seus motores produzem\(\displaystyle 1.250×10^7N\) empuxo, e a resistência do ar é\(\displaystyle 4.50×10^6N\). Qual é a aceleração do foguete? Mostre explicitamente como você segue as etapas da Estratégia de Solução de Problemas para as leis do movimento de Newton.
Solução
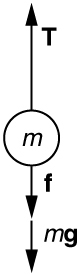
Usando o diagrama de corpo livre:
\(\displaystyle F_{net}=T−f−mg=ma\)
para que
\(\displaystyle a=\frac{T−f−mg}{m}=\frac{1.250×10^7N−4.50×10^6N−(5.00×10^5kg)(9.80 m/s^2)}{5.00×10^5kg}=6.20m/s^2\)
51. As rodas de um carro de médio porte exercem uma força de 2100 N para trás na estrada para acelerar o carro na direção para frente. Se a força de atrito, incluindo a resistência do ar, for de 250 N e a aceleração do carro for\(\displaystyle 1.80 m/s^2\), qual é a massa do carro mais seus ocupantes? Mostre explicitamente como você segue as etapas da Estratégia de Solução de Problemas para as leis do movimento de Newton. Para essa situação, desenhe um diagrama de corpo livre e escreva a equação da força líquida.
52. Calcule a força que um saltador de 70,0 kg de altura deve exercer no solo para produzir uma aceleração ascendente 4,00 vezes a aceleração devido à gravidade. Mostre explicitamente como você segue as etapas da Estratégia de Solução de Problemas para as leis do movimento de Newton.
Solução
1. Use as leis do movimento de Newton.
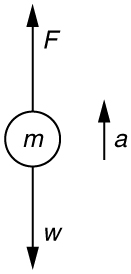
2. Dado:\(\displaystyle a=4.00g=(4.00)(9.80 m/s^2)=39.2m/s^2; m=70.0 kg.\)
Encontre:\(\displaystyle F\)
3. \(\displaystyle \sum{F=+F−w=ma,}\)de modo que\(\displaystyle F=ma+w=ma+mg=m(a+g)\)
\(\displaystyle F=(70.0 kg)[(39.2 m/s^2)+(9.80 m/s^2)]=3.43×10^3N\) a força exercida pelo saltador em altura está na verdade no chão, mas F tamanho 12 {F} está levantado do chão e o faz pular.
4. Esse resultado é razoável, pois é bem possível que uma pessoa exerça uma força da magnitude de\(\displaystyle 10^3N\)
53. Ao pousar após uma cambalhota espetacular, uma ginasta de 40,0 kg desacelera ao empurrar diretamente para baixo no tapete. Calcule a força que ela deve exercer se sua desaceleração for 7,00 vezes a aceleração devido à gravidade. Mostre explicitamente como você segue as etapas da Estratégia de Solução de Problemas para as leis do movimento de Newton.
54. Um trem de carga consiste em dois\(\displaystyle 8.00×10^4-kg\) motores e 45 carros com massas médias de\(\displaystyle 5.50×10^4kg\).
(a) Que força cada motor deve exercer para trás na pista para acelerar o trem a uma taxa de\(\displaystyle 5.00×10^{–2}m/s^2\) se a força de atrito for\(\displaystyle 7.50×10^5N\), assumindo que os motores exercem forças idênticas? Essa não é uma grande força de atrito para um sistema tão grande. O atrito de rolamento dos trens é pequeno e, consequentemente, os trens são sistemas de transporte muito eficientes em termos de energia.
(b) Qual é a força no acoplamento entre os 37º e 38º carros (essa é a força que cada um exerce sobre o outro), supondo que todos os carros tenham a mesma massa e que o atrito seja distribuído uniformemente entre todos os carros e motores?
Solução
(a)\(\displaystyle 4.41×10^5N\)
(b)\(\displaystyle 1.50×10^5N\)
55. Às vezes, aviões comerciais são empurrados para fora da área de carregamento de passageiros por um trator.
(a) Um trator de 1800 kg exerce uma força de\(\displaystyle 1.75×10^4N\) retrocesso no pavimento, e o sistema experimenta forças de resistência ao movimento que totalizam 2400 N. Se a aceleração for\(\displaystyle 0.150 m/s^2\), qual é a massa do avião?
(b) Calcule a força exercida pelo trator no avião, assumindo que 2200 N do atrito sejam experimentados pelo avião.
(c) Desenhe dois esboços mostrando os sistemas de interesse usados para resolver cada parte, incluindo os diagramas de corpo livre para cada uma.
56. Um carro de 1100 kg puxa um barco em um trailer.
(a) Qual força total resiste ao movimento do carro, barco e reboque, se o carro exerce uma força de 1900-N na estrada e produz uma aceleração de\(\displaystyle 0.550 m/s^2\)? A massa do barco mais o reboque é de 700 kg.
(b) Qual é a força no engate entre o carro e o trailer se 80% das forças de resistência forem experimentadas pelo barco e pelo reboque?
Solução
(a)\(\displaystyle 910 N\)
(b)\(\displaystyle 1.11×10^3N\)
57. (a) Encontre as magnitudes das forças\(\displaystyle F_1\) e\(\displaystyle F_2\) que somam para dar a força total\(\displaystyle F_{tot}\) mostrada na Figura. Isso pode ser feito graficamente ou usando trigonometria.
(b) Mostre graficamente que a mesma força total é obtida independentemente da ordem de adição de\(\displaystyle F_1\) e\(\displaystyle F_2\)
(c) Encontre a direção e a magnitude de algum outro par de vetores que somam para dar\(\displaystyle F_{tot}\). Desenhe-os em escala no mesmo desenho usado na parte (b) ou em uma imagem similar.
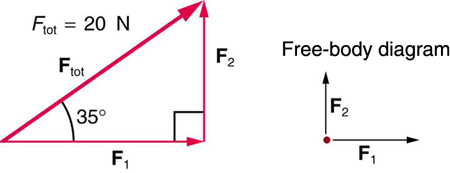
58. Duas crianças puxam uma terceira criança em um trenó de disco de neve exercendo forças\(\displaystyle F_1\)\(\displaystyle F_2\), conforme mostrado acima na Figura. Encontre a aceleração do sistema de trenó e criança de 49,00 kg. Observe que a direção da força de atrito não é especificada; ela estará na direção oposta da soma de\(\displaystyle F_1\)\(\displaystyle F_2\) e.
Solução
\(\displaystyle a=0.139 m/s, θ=12.4º\) ao norte do leste
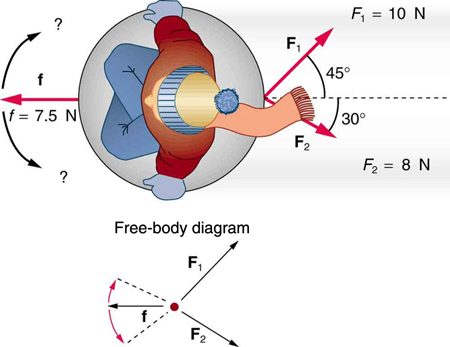
Uma visão aérea de uma criança sentada em um trenó de disco de neve.
59. Suponha que seu carro esteja profundamente atolado na lama e você queira usar o método ilustrado na Figura para retirá-lo.
(a) Que força você teria que exercer perpendicularmente ao centro da corda para produzir uma força de 12.000 N no carro se o ângulo fosse 2,00°? Nesta parte, mostre explicitamente como você segue as etapas da Estratégia de Solução de Problemas para as leis do movimento de Newton.
(b) Cordas reais se estendem sob tais forças. Que força seria exercida no carro se o ângulo aumentasse para 7,00° e você ainda aplicasse a força encontrada na parte (a) em seu centro?

60. Qual força é exercida no dente na Figura se a tensão no fio for 25,0 N? Observe que a força aplicada ao dente é menor do que a tensão no fio, mas isso é necessário devido a considerações práticas de como a força pode ser aplicada na boca. Mostre explicitamente como você segue as etapas da Estratégia de Solução de Problemas para as leis do movimento de Newton.
Solução
1. Use as leis de Newton, pois estamos procurando forças.
2. Desenhe um diagrama de corpo livre:
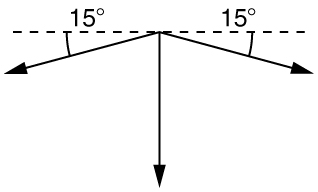
3. A tensão é dada como\(\displaystyle T=25.0 N\). Encontre\(\displaystyle F_{app}\). Usar as leis de Newton dá:\(\displaystyle Σ F_y=0\), de modo que a força aplicada é devida aos componentes y das duas tensões:\(\displaystyle F_{app}=2Tsinθ=2(25.0 N)sin(15º)=12.9 N\)
Os componentes x da tensão são cancelados. \(\displaystyle ∑F_x=0\).
4. Isso parece razoável, pois as tensões aplicadas devem ser maiores do que a força aplicada ao dente.
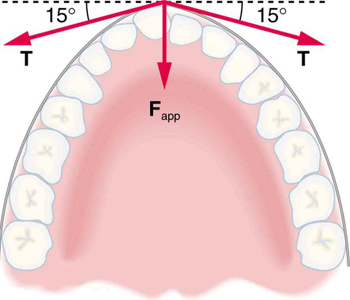
Os aparelhos ortodônticos são usados para aplicar forças nos dentes para realinhá-los. Nesta figura são mostradas as tensões aplicadas pelo fio ao dente saliente. A força total aplicada ao dente pelo fio,\(\displaystyle F_{app}\), aponta diretamente para a parte posterior da boca.
61. A figura mostra o super-herói e o Trusty Sidekick pendurados imóveis em uma corda. A massa do super-herói é 90,0 kg, enquanto a do Trusty Sidekick é 55,0 kg e a massa da corda é insignificante.
(a) Desenhe um diagrama de corpo livre da situação mostrando todas as forças atuando sobre Super-Herói, Trusty Sidekick e a corda.
(b) Encontre a tensão na corda acima do Super-herói.
(c) Encontre a tensão na corda entre Superhero e Trusty Sidekick. Indique em seu diagrama de corpo livre o sistema de interesse usado para resolver cada peça.

Super-herói e Trusty Sidekick ficam imóveis em uma corda enquanto tentam descobrir o que fazer a seguir. A tensão será a mesma em todos os lugares da corda?
62. Uma enfermeira empurra um carrinho exercendo uma força na alça em um ângulo descendente\(\displaystyle 35.0º\) abaixo da horizontal. O carrinho carregado tem uma massa de 28,0 kg e a força de atrito é de 60,0 N.
(a) Desenhe um diagrama de corpo livre para o sistema de interesse.
(b) Que força a enfermeira deve exercer para se mover a uma velocidade constante?
63. Construa seu próprio problema
Considere a tensão no cabo do elevador durante o tempo em que o elevador parte do repouso e acelera sua carga para cima até uma certa velocidade de cruzeiro. Considerando o elevador e sua carga como o sistema de interesse, desenhe um diagrama de corpo livre. Em seguida, calcule a tensão no cabo. Entre as coisas a considerar estão a massa do elevador e sua carga, a velocidade final e o tempo necessário para atingir essa velocidade.
64. Construa seu próprio problema
Considere duas pessoas empurrando um tobogã com quatro crianças em uma encosta coberta de neve. Crie um problema no qual você calcule a aceleração do tobogã e sua carga. Inclua um diagrama de corpo livre do sistema de interesse apropriado como base para sua análise. Mostre as forças vetoriais e seus componentes e explique a escolha das coordenadas. Entre as coisas a serem consideradas estão as forças exercidas por quem empurra, o ângulo da inclinação e as massas do tobogã e das crianças.
65. Resultados irracionais
(a) Repita o exercício, mas suponha que uma aceleração de\(\displaystyle 1.20 m/s^2\) seja produzida.
(b) O que não é razoável no resultado?
(c) Qual premissa não é razoável e por que não é razoável?
66. Resultados irracionais
(a) Qual é a aceleração inicial de um foguete que tem uma massa de\(\displaystyle 1.50×10^6kg\) na decolagem, cujos motores produzem um empuxo de\(\displaystyle 2.00×10^6N\)? Não negligencie a gravidade.
(b) O que não é razoável no resultado? (Esse resultado foi alcançado involuntariamente por vários foguetes reais.)
(c) Quais premissas não são razoáveis ou quais premissas são inconsistentes? (Você pode achar útil comparar esse problema com o problema do foguete anteriormente nesta seção.)
4.7: Outras aplicações das Leis do Movimento de Newton
67. Uma pulga salta exercendo uma força\(\displaystyle 1.20×10^{−5}N\) reta no chão. Uma brisa que sopra na pulga paralela ao solo exerce uma força\(\displaystyle 0.500×10^{−6}N\) sobre a pulga. Encontre a direção e a magnitude da aceleração da pulga se sua massa for\(\displaystyle 6.00×10^{−7}kg\). Não negligencie a força gravitacional.
Solução
\(\displaystyle 10.2m/s^2, 4.67º\) da vertical
68. Dois músculos na parte de trás da perna puxam para cima o tendão de Aquiles, conforme mostrado na Figura. (Esses músculos são chamados de cabeças medial e lateral do músculo gastrocnêmio.) Encontre a magnitude e a direção da força total no tendão de Aquiles. Que tipo de movimento poderia ser causado por essa força?
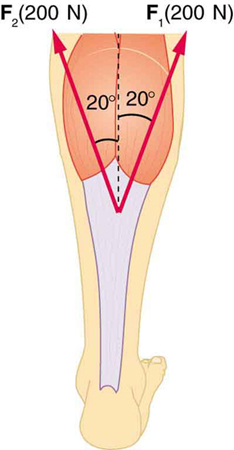
Tendão de Aquiles
69. Uma pessoa de 76,0 kg está sendo retirada de um prédio em chamas, conforme mostrado na Figura. Calcule a tensão nas duas cordas se a pessoa estiver momentaneamente imóvel. Inclua um diagrama de corpo livre em sua solução.
Solução
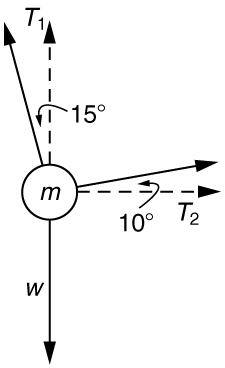
\(\displaystyle T_1=736 N\)
\(\displaystyle T_2=194 N\)
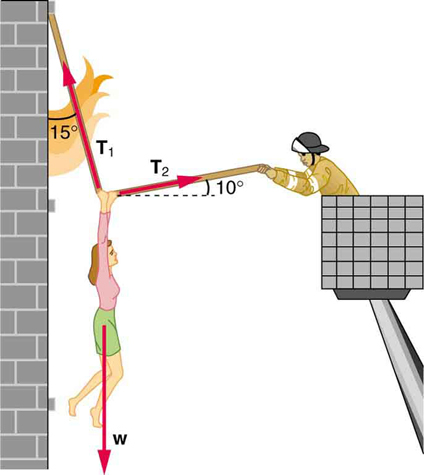
A força\(\displaystyle T_2\) necessária para manter firme a pessoa que está sendo resgatada do fogo é menor que seu peso e menor que o\(\displaystyle T_1\) tamanho da força 12 {T RSub {tamanho 8 {1}}} {} na outra corda, já que a corda mais vertical suporta uma parte maior de seu peso (uma vertical força).
70. Conceitos integrados
Um golfinho de 35,0 kg desacelera de 12,0 para 7,50 m/s em 2,30 s para se juntar a outro golfinho em jogo. Que força média foi exercida para retardá-lo se ele estivesse se movendo horizontalmente? (A força gravitacional é equilibrada pela força de empuxo da água.)
71. Conceitos integrados
Ao iniciar uma corrida a pé, um velocista de 70,0 kg exerce uma força média de 650 N para trás no solo por 0,800 s.
(a) Qual é a velocidade final dele?
(b) Até onde ele viaja?
Solução
(a)\(\displaystyle 7.43 m/s\)
(b)\(\displaystyle 2.97 m\)
72 . Conceitos integrados
Um grande foguete tem uma massa de\(\displaystyle 2.00×10^6kg\) na decolagem, e seus motores produzem um empuxo de\(\displaystyle 3.50×10^7N\).
(a) Encontre sua aceleração inicial se ela decolar verticalmente.
(b) Quanto tempo é necessário para atingir uma velocidade de 120 km/h em linha reta, assumindo massa e empuxo constantes?
(c) Na realidade, a massa de um foguete diminui significativamente à medida que seu combustível é consumido. Descreva qualitativamente como isso afeta a aceleração e o tempo desse movimento.
73. Conceitos integrados
Um jogador de basquete pula direto para pegar uma bola. Para fazer isso, ele abaixa o corpo em 0,300 m e depois acelera nessa distância endireitando as pernas com força. Este jogador sai do chão com uma velocidade vertical suficiente para carregá-lo 0,900 m acima do chão.
(a) Calcule sua velocidade quando ele sair do chão.
(b) Calcule sua aceleração enquanto ele endireita as pernas. Ele vai de zero até a velocidade encontrada na parte (a) em uma distância de 0,300 m.
(c) Calcule a força que ele exerce no chão para fazer isso, já que sua massa é de 110 kg.
Solução
(a)\(\displaystyle 4.20 m/s\)
(b)\(\displaystyle 29.4m/s^2\)
(c)\(\displaystyle 4.31×10^3N\)
74. Conceitos integrados
Um projétil de fogos de artifício de 2,50 kg é disparado diretamente de um morteiro e atinge uma altura de 110 m.
(a) Negligenciando a resistência do ar (uma suposição ruim, mas faremos isso neste exemplo), calcule a velocidade da concha quando ela sair da argamassa.
(b) A argamassa em si é um tubo de 0,450 m de comprimento. Calcule a aceleração média da concha no tubo à medida que ela vai de zero até a velocidade encontrada em (a).
(c) Qual é a força média na casca da argamassa? Expresse sua resposta em newtons e como uma proporção com o peso da casca.
75. Exercício de repetição de conceitos integrados para um projétil disparado em um ângulo\(\displaystyle 10.0º\) da vertical.
Solução
(a)\(\displaystyle 47.1 m/s\)
(b)\(\displaystyle 2.47×10^3m/s^2\)
(c)\(\displaystyle 6.18×10^3N\).
76. Conceitos integrados
Um elevador cheio de passageiros tem uma massa de 1700 kg.
(a) O elevador acelera para cima do repouso a uma taxa de\(\displaystyle 1.20 m/s^2\). Calcule a tensão no cabo que suporta o elevador.
(b) O elevador continua subindo em velocidade constante por 8,50 s. Qual é a tensão no cabo durante esse período?
(c) O elevador desacelera a uma taxa\(\displaystyle 0.600 m/s^2\) de 3,00 s. Qual é a tensão no cabo durante a desaceleração?
(d) Até que ponto o elevador se moveu acima de seu ponto de partida original e qual é sua velocidade final?
77. Resultados irracionais
(a) Qual é a velocidade final de um carro originalmente viajando a 50,0 km/h que desacelera a uma taxa\(\displaystyle 0.400 m/s^2\) de 50,0 s?
(b) O que não é razoável no resultado?
(c) Quais premissas não são razoáveis ou quais premissas são inconsistentes?
78. Resultados irracionais
Um homem de 75,0 kg está em uma balança de banheiro em um elevador que acelera do repouso para 30,0 m/s em 2,00 s.
(a) Calcule a leitura da balança em newtons e compare-a com seu peso. (A balança exerce uma força ascendente sobre ele igual à sua leitura.)
(b) O que não é razoável no resultado?
(c) Quais premissas não são razoáveis ou quais premissas são inconsistentes?
4.8: Tópico estendido: As quatro forças básicas — uma introdução
79. (a) Qual é a força da força nuclear fraca em relação à força nuclear forte?
(b) Qual é a força da força nuclear fraca em relação à força eletromagnética? Como a força nuclear fraca atua apenas em distâncias muito curtas, como dentro de núcleos, onde as forças fortes e eletromagnéticas também atuam, pode parecer surpreendente que tenhamos algum conhecimento disso. Temos esse conhecimento porque a fraca força nuclear é responsável pelo decaimento beta, um tipo de decaimento nuclear não explicado por outras forças.
Solução
(a)\(\displaystyle 1×10^{−13}\)
(b)\(\displaystyle 1×10^{−11}\)
80. (a) Qual é a razão entre a força gravitacional e a força nuclear forte?
(b) Qual é a razão entre a força gravitacional e a força nuclear fraca?
(c) Qual é a razão entre a força da força gravitacional e a força eletromagnética? O que suas respostas sugerem sobre a influência da força gravitacional nos núcleos atômicos?
81. Qual é a razão entre a força da força nuclear forte e a da força eletromagnética? Com base nessa proporção, você pode esperar que a força forte domine o núcleo, o que vale para núcleos pequenos. Núcleos grandes, no entanto, têm tamanhos maiores do que o alcance da força nuclear forte. Nesses tamanhos, a força eletromagnética começa a afetar a estabilidade nuclear. Esses fatos serão usados para explicar a fusão nuclear e a fissão posteriormente neste texto.
Solução
\(\displaystyle 10^2\)


