2.1: Deslocamento

Last updated
Save as PDF

Page ID: 194283

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Defina a posição, o deslocamento, a distância e a distância percorrida.
Explique a relação entre posição e deslocamento.
Faça a distinção entre deslocamento e distância percorrida.
Calcule o deslocamento e a distância com base na posição inicial, na posição final e no caminho entre os dois.

Esses ciclistas no Vietnã podem ser descritos por sua posição em relação aos edifícios e a um canal. Seu movimento pode ser descrito por sua mudança de posição, ou deslocamento, no quadro de referência.

Três pessoas andando de bicicleta ao longo de um canal. Os edifícios borrados ao fundo transmitem uma sensação de movimento dos ciclistas. — Figura\( \PageIndex{1}\): Esses ciclistas no Vietnã podem ser descritos por sua posição em relação a edifícios e a um canal. Seu movimento pode ser descrito por sua mudança de posição, ou deslocamento, no quadro de referência. (crédito: Suzan Black, Fotopedia)

Posição

Para descrever o movimento de um objeto, primeiro você deve ser capaz de descrever sua posição — onde ele está em um determinado momento. Mais precisamente, você precisa especificar sua posição em relação a um quadro de referência conveniente. A Terra é frequentemente usada como um quadro de referência, e geralmente descrevemos a posição de um objeto no que se refere a objetos estacionários nesse quadro de referência. Por exemplo, o lançamento de um foguete seria descrito em termos da posição do foguete em relação à Terra como um todo, enquanto a posição de um professor poderia ser descrita em termos de onde ela está em relação ao quadro branco próximo. Em outros casos, usamos quadros de referência que não são estacionários, mas estão em movimento em relação à Terra. Para descrever a posição de uma pessoa em um avião, por exemplo, usamos o avião, não a Terra, como referência.

Deslocamento

Se um objeto se move em relação a um quadro de referência (por exemplo, se um professor se move para a direita em relação a um quadro branco ou um passageiro se move em direção à parte traseira de um avião), a posição do objeto muda. Essa mudança de posição é conhecida como deslocamento. A palavra “deslocamento” implica que um objeto se moveu ou foi deslocado.

Definição: Deslocamento

O deslocamento é a mudança na posição de um objeto:

\(Δx=x_f−x_0,\)

onde\(Δx\) é o deslocamento,\(x_f\) é a posição final e\(x_0\) é a posição inicial.

Neste texto, o tamanho da letra grega maiúscula\(Δ\) (delta) sempre significa “mudança” em qualquer quantidade seguinte; portanto, tamanho\(Δx\) significa mudança de posição. Sempre resolva o deslocamento subtraindo o tamanho\(x_0\) da posição inicial da posição final\(x_f\).

Observe que a unidade SI para deslocamento é o metro (\(m\)) (consulte a Seção sobre Quantidades e Unidades Físicas), mas às vezes quilômetros, milhas, pés e outras unidades de comprimento são usados. Lembre-se de que quando unidades diferentes do medidor são usadas em um problema, talvez seja necessário convertê-las em metros para concluir o cálculo.

A posição inicial e final de uma professora enquanto ela se move para a direita enquanto escreve em um quadro branco. Sua posição inicial é de 1 ponto a 5 metros. Sua posição final é de 3 pontos a 5 metros. Seu deslocamento é dado pela equação delta x igual a x sub f menos x sub 0 é igual a 2 ponto 0 metros. — Figura\( \PageIndex{2}\): Um professor caminha para a esquerda e para a direita enquanto leciona. Sua posição em relação à Terra é dada por x. O deslocamento de +2 m do professor em relação à Terra é representado por uma seta apontando para a direita.

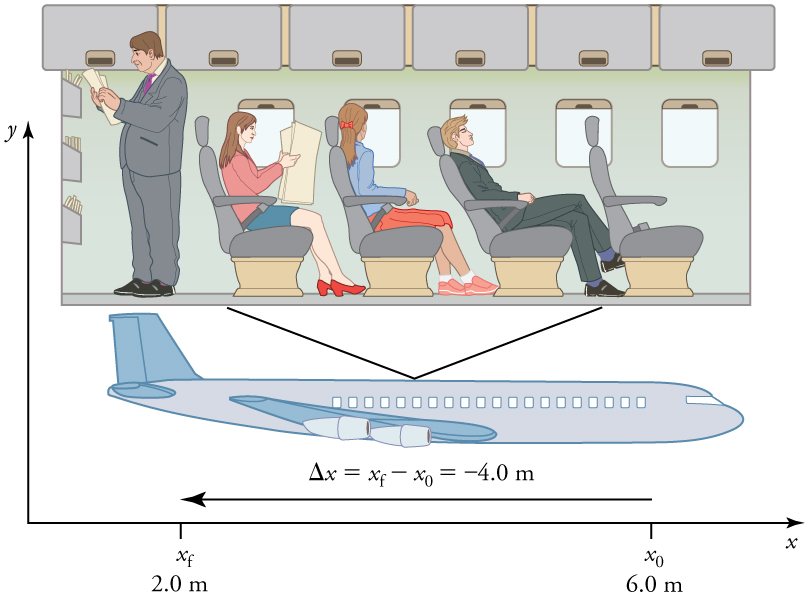
Vista de um avião com uma inserção dos passageiros sentados lá dentro. Um passageiro acabou de sair de seu assento e agora está de pé na parte de trás. Sua posição inicial era de 6 ponto 0 metros. Sua posição final é de 2 pontos a 0 metros. Seu deslocamento é dado pela equação delta x igual a x sub f menos x sub 0 igual a 4 ponto zero metros. — Figura\( \PageIndex{3}\): Um passageiro se move de seu assento para a parte de trás do avião. Sua localização em relação ao avião é dada por x. O deslocamento de -4 m do passageiro em relação ao avião é representado por uma seta em direção à parte traseira do avião. Observe que a flecha representando seu deslocamento é duas vezes maior que a seta que representa o deslocamento do professor (ele se move duas vezes mais longe)

Observe que o deslocamento tem uma direção e uma magnitude. O deslocamento do professor na Figura\( \PageIndex{2}\) é de 2,0 m para a direita e o deslocamento do passageiro da companhia aérea é de 4,0 m para trás na Figura\( \PageIndex{3}\). No movimento unidimensional, a direção pode ser especificada com um sinal de mais ou menos. Ao iniciar um problema, você deve selecionar qual direção é positiva (geralmente será para a direita ou para cima, mas você pode selecionar positiva como sendo qualquer direção). A posição inicial do professor é tamanho x ₀ = 1,5 m e sua posição final é x _f = 3,5 m. Portanto, seu deslocamento é

\[\begin{align*} Δx &=x_f−x_0 \\[5pt] &=3.5\, m−1.5\, m \\[5pt] &=+2.0\, m. \end{align*}\]

Nesse sistema de coordenadas, o movimento para a direita é positivo, enquanto o movimento para a esquerda é negativo. Da mesma forma, a posição inicial do passageiro do avião é\(\displaystyle x_0=6.0 m\) e sua posição final é\(\displaystyle x_f=2.0 m\), então seu deslocamento é

\[\begin{align*} Δx&=x_f−x_0 \\[5pt] &= 2.0\, m−6.0\, m \\[5pt] &=−4.0\, m.\end{align*}\]

Seu deslocamento é negativo porque seu movimento está em direção à parte traseira do avião, ou na direção negativa de tamanho 12 {x} {} em nosso sistema de coordenadas.

Distância

Embora o deslocamento seja descrito em termos de direção, a distância não é. A distância é definida como a magnitude ou o tamanho do deslocamento entre duas posições. Observe que a distância entre duas posições não é a mesma que a distância percorrida entre elas. A distância percorrida é o comprimento total do caminho percorrido entre duas posições. A distância não tem direção e, portanto, nenhum sinal. Por exemplo, a distância percorrida pelo professor é de 2,0 m e a distância percorrida pelo passageiro do avião é de 4,0 m.

Alerta de equívoco: distância percorrida versus magnitude do deslocamento

É importante observar que a distância percorrida, no entanto, pode ser maior que a magnitude do deslocamento (por magnitude, queremos dizer apenas o tamanho do deslocamento sem levar em conta sua direção; ou seja, apenas um número com uma unidade). Por exemplo, a professora podia andar de um lado para o outro várias vezes, talvez caminhando uma distância de 150 m durante uma palestra, mas ainda assim acabava apenas 2,0 m à direita do ponto de partida. Nesse caso, seu deslocamento seria de +2,0 m, a magnitude de seu deslocamento seria de 2,0 m, mas a distância que ela percorreu seria de 150 m. Na cinemática, quase sempre lidamos com o deslocamento e a magnitude do deslocamento, e quase nunca com a distância percorrida. Uma maneira de pensar sobre isso é supor que você marcou o início e o fim do movimento. O deslocamento é simplesmente a diferença na posição das duas marcas e é independente do caminho percorrido ao viajar entre as duas marcas. A distância percorrida, no entanto, é o comprimento total do caminho percorrido entre as duas marcas.

Exercício\(\PageIndex{1}\)

Um ciclista anda 3 km a oeste e depois dá meia volta e pedala 2 km para o leste.

Qual é o deslocamento dela?
Que distância ela percorre?
Qual é a magnitude de seu deslocamento?

Resposta
Responda a: O deslocamento do piloto é\(\displaystyle Δ_x=x_f−x_0=−1 km\). (O deslocamento é negativo porque consideramos que o leste é positivo e o oeste é negativo.)
Resposta b: A distância percorrida é\(\displaystyle 3 km+2 km=5 km\).
Resposta c: A magnitude do deslocamento é\(\displaystyle 1 km\).

Resumo

Cinemática é o estudo do movimento sem considerar suas causas. Neste capítulo, ele se limita ao movimento ao longo de uma linha reta, chamada movimento unidimensional.
O deslocamento é a mudança na posição de um objeto.
Em símbolos, o deslocamento\(\displaystyle Δx\) é definido como

\(\displaystyle Δx=x_f−x_0\),

onde\(\displaystyle x_0\) é a posição inicial e xf é a posição final. Neste texto, a letra grega\(\displaystyle Δ\) (delta) sempre significa “mudança” em qualquer quantidade que a siga. A unidade SI para deslocamento é o medidor (m). O deslocamento tem uma direção e uma magnitude.

Ao iniciar um problema, atribua qual direção será positiva.
A distância é a magnitude do deslocamento entre duas posições.
A distância percorrida é o comprimento total do caminho percorrido entre duas posições.

Glossário

cinemática: o estudo do movimento sem considerar suas causas

posição: a localização de um objeto em um determinado momento

deslocamento: a mudança na posição de um objeto

distância: a magnitude do deslocamento entre duas posições

distância percorrida: o comprimento total do caminho percorrido entre duas posições