2.E: Cinemática (exercícios)
- Page ID
- 194262
Perguntas conceituais
2.1: Deslocamento
1. Dê um exemplo em que há distinções claras entre distância percorrida, deslocamento e magnitude do deslocamento. Identifique especificamente cada quantidade em seu exemplo.
2. Em que circunstâncias a distância percorrida é igual à magnitude do deslocamento? Qual é o único caso em que a magnitude do deslocamento e do deslocamento são exatamente iguais?
3. As bactérias se movem para frente e para trás usando seus flagelos (estruturas que parecem pequenas caudas). Velocidades de até\(\displaystyle 50 μm/s(50×10^{−6}m/s)\) terem sido observadas. A distância total percorrida por uma bactéria é grande para seu tamanho, enquanto seu deslocamento é pequeno. Por que isso?
2.2: Vetores, escalares e sistemas de coordenadas
4. Um estudante escreve: “Um pássaro que está mergulhando em busca de presas tem uma velocidade de\(\displaystyle −10m/s\)” O que há de errado com a declaração do aluno? O que o aluno realmente descreveu? Explique.
5. Qual é a velocidade do pássaro no Exercício?
6. A aceleração é a mudança na velocidade ao longo do tempo. Dada essa informação, a aceleração é um vetor ou uma grandeza escalar? Explique.
7. Uma previsão do tempo afirma que a temperatura está prevista para\(\displaystyle −5ºC\) o dia seguinte. Essa temperatura é um vetor ou uma grandeza escalar? Explique.
2.3: Tempo, velocidade e velocidade
8. Dê um exemplo (mas não um do texto) de um dispositivo usado para medir o tempo e identificar qual alteração nesse dispositivo indica uma mudança no tempo.
9. Há uma distinção entre a velocidade média e a magnitude da velocidade média. Dê um exemplo que ilustra a diferença entre essas duas quantidades.
10. O odômetro de um carro mede a posição ou o deslocamento? Seu velocímetro mede a velocidade ou a velocidade?
11. Se você dividir a distância total percorrida em uma viagem de carro (conforme determinado pelo odômetro) pelo tempo da viagem, você está calculando a velocidade média ou a magnitude da velocidade média? Sob quais circunstâncias essas duas quantidades são iguais?
12. Como a velocidade instantânea e a velocidade instantânea se relacionam entre si? Como eles diferem?
2.4: Aceleração
13. É possível que a velocidade seja constante enquanto a aceleração não é zero? Dê um exemplo dessa situação.
14. É possível que a velocidade seja constante enquanto a aceleração não é zero? Explique.
15. Dê um exemplo em que a velocidade é zero, mas a aceleração não é.
16. Se um trem do metrô está se movendo para a esquerda (tem uma velocidade negativa) e depois para, qual é a direção de sua aceleração? A aceleração é positiva ou negativa?
17. Os sinais de mais e menos são usados em movimentos unidimensionais para indicar a direção. Qual é o sinal de uma aceleração que reduz a magnitude de uma velocidade negativa? De uma velocidade positiva?
2.6: Fundamentos da solução de problemas para cinemática unidimensional
18. Quais informações você precisa para escolher qual equação ou equações usar para resolver um problema? Explique.
19. Qual é a última coisa que você deve fazer ao resolver um problema? Explique.
2.7: Objetos caindo
20. Qual é a aceleração de uma rocha lançada diretamente para cima na subida? No topo do voo? No caminho para baixo?
21. Um objeto que é lançado diretamente cai de volta para a Terra. Isso é movimento unidimensional.
(a) Quando sua velocidade é zero?
(b) Sua velocidade muda de direção?
(c) A aceleração devido à gravidade tem o mesmo sinal na subida e na descida?
22. Suponha que você jogue uma pedra quase reta em um coco em uma palmeira, e a pedra erra na subida, mas atinge o coco na descida. Negligenciando a resistência do ar, como a velocidade da rocha ao atingir o coco na descida se compara com a que teria sido se tivesse atingido o coco na subida? É mais provável que o coco se desloque ao subir ou descer? Explique.
23. Se um objeto for lançado diretamente e a resistência do ar for insignificante, sua velocidade ao retornar ao ponto de partida é a mesma de quando foi lançado. Se a resistência do ar não fosse insignificante, como sua velocidade de retorno se compararia à velocidade inicial? Como a altura máxima até a qual ele sobe seria afetada?
24. A severidade de uma queda depende da sua velocidade quando você atinge o solo. Todos os fatores, exceto a aceleração devido à gravidade sendo a mesma, quantas vezes maior poderia ser uma queda segura na Lua do que na Terra (a aceleração gravitacional na Lua é cerca de 1/6 da da Terra)?
25. Quantas vezes mais alto um astronauta poderia pular na Lua do que na Terra se sua velocidade de decolagem fosse a mesma em ambos os locais (a aceleração gravitacional na Lua é de cerca de 1/6 da\(\displaystyle g\) Terra)?
2.8: Análise gráfica do movimento unidimensional
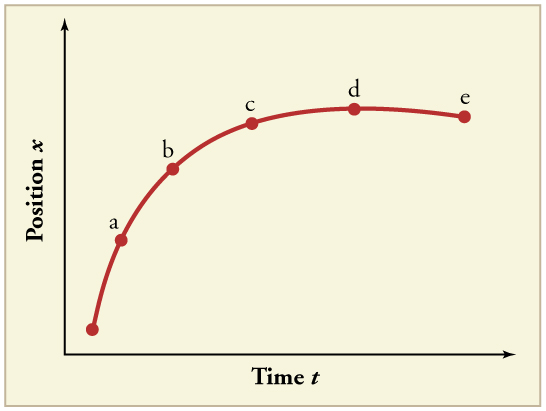
23. (a) Explique como você pode usar o gráfico de posição versus tempo na Figura para descrever a mudança na velocidade ao longo do tempo. Identifique
(b) o tempo (\(\displaystyle t_a, t_b, t_c, t_d,\)ou\(\displaystyle t_e\)) em que a velocidade instantânea é maior,
(c) o momento em que é zero, e
(d) o momento em que é negativo.
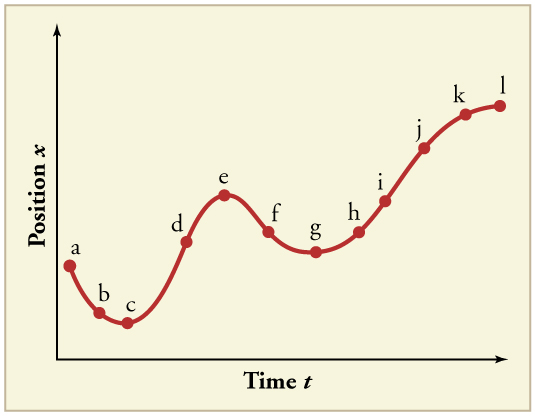
24. (a) Esboce um gráfico de velocidade versus tempo correspondente ao gráfico de posição versus tempo dado na Figura.
(b) Identifique o tempo ou horários (\(\displaystyle t_a, t_b, t_c\), etc.) em que a velocidade instantânea é maior.
(c) Em quais momentos é zero?
(d) Em quais momentos é negativo?
25. (a) Explique como você pode determinar a aceleração ao longo do tempo a partir de um gráfico de velocidade versus tempo, como o da Figura.
(b) Com base no gráfico, como a aceleração muda ao longo do tempo?
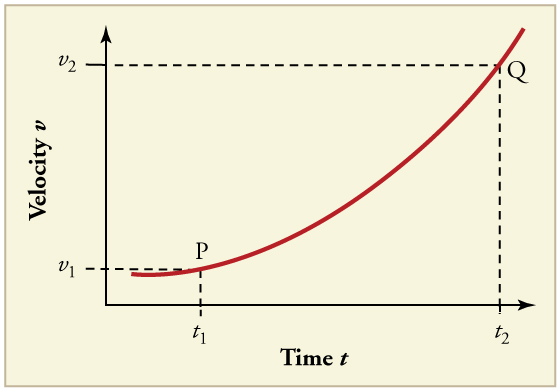
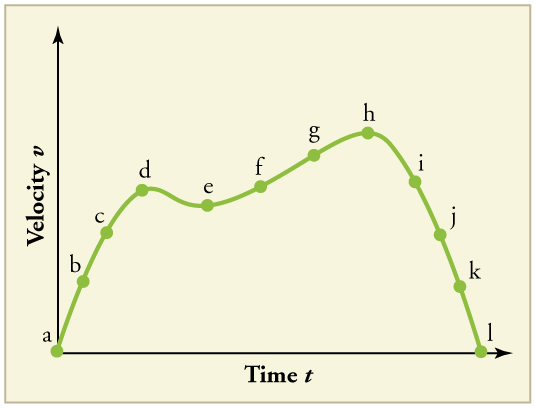
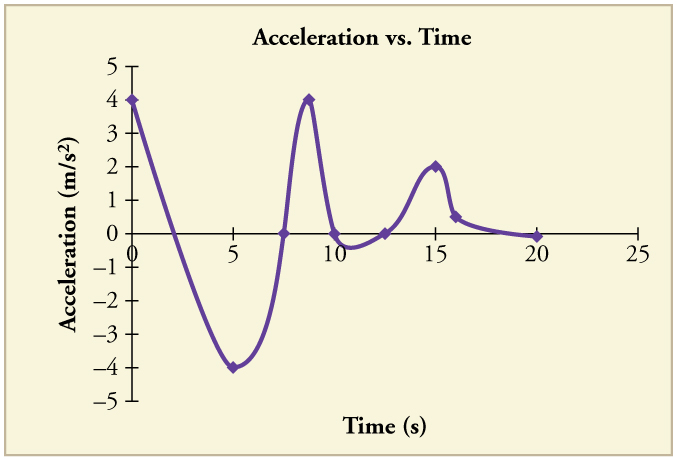
26. (a) Esboce um gráfico de aceleração versus tempo correspondente ao gráfico de velocidade versus tempo dado na Figura.
(b) Identifique o momento ou horários (\(\displaystyle t_a, t_b, t_c,\)etc.) em que a aceleração é maior.
(c) Em quais momentos é zero?
(d) Em quais momentos é negativo?
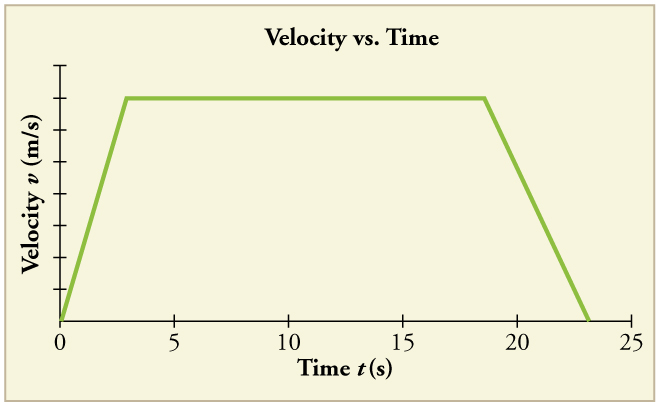
27. Considere o gráfico de velocidade versus tempo de uma pessoa em um elevador mostrado na Figura. Suponha que o elevador esteja inicialmente em repouso. Em seguida, ele acelera por 3 segundos, mantém essa velocidade por 15 segundos e depois desacelera por 5 segundos até parar. A aceleração de toda a viagem não é constante, então não podemos usar as equações de movimento das Equações de Movimento para Aceleração Constante em Uma Dimensão para a viagem completa. (No entanto, poderíamos usá-los nas três seções individuais em que a aceleração é uma constante.) Desenhe gráficos de
(a) posição versus tempo e
(b) aceleração versus tempo para esta viagem.
28. Um cilindro é empurrado e, em seguida, enrola em um plano inclinado. Se a origem for o ponto de partida, desenhe a posição, a velocidade e a aceleração do cilindro versus o tempo à medida que ele sobe e depois desce no plano.
Problemas e exercícios
2.1: Deslocamento
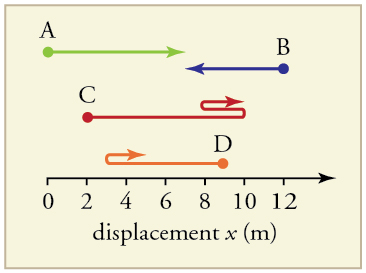
29. Encontre o seguinte para o caminho A:
(a) A distância percorrida.
(b) A magnitude do deslocamento do início ao fim.
(c) O deslocamento do início ao fim.
Solução
(a) 7 m
(b) 7 m
(c)\(\displaystyle +7m\)
30. Encontre o seguinte para o caminho B:
(a) A distância percorrida.
(b) A magnitude do deslocamento do início ao fim.
(c) O deslocamento do início ao fim.
31. Encontre o seguinte para o caminho C:
(a) A distância percorrida.
(b) A magnitude do deslocamento do início ao fim.
(c) O deslocamento do início ao fim.
Solução
(a) 13 m
(b) 9 m
(c)\(\displaystyle +9m\)
32. Encontre o seguinte para o caminho D:
(a) A distância percorrida.
(b) A magnitude do deslocamento do início ao fim
(c) O deslocamento do início ao fim
2.3: Tempo, velocidade e velocidade
33. (a) Calcule a velocidade média da Terra em relação ao Sol.
(b) Qual é sua velocidade média em um período de um ano?
Solução
(a)\(\displaystyle 3.0×10^4m/s\)
(b) 0 m/s
34. A lâmina de um helicóptero gira exatamente a 100 rotações por minuto. Sua ponta está a 5,00 m do centro de rotação.
(a) Calcule a velocidade média da ponta da pá no quadro de referência do helicóptero
(b) Qual é sua velocidade média em uma revolução?
35. Os continentes norte-americano e europeu estão se afastando a uma taxa de cerca de 3 cm/ano. Nesse ritmo, quanto tempo eles levarão para se afastarem 500 km mais longe do que estão atualmente?
Solução
\(\displaystyle 2×10^7years\)
36. A terra a oeste da falha de San Andreas, no sul da Califórnia, está se movendo a uma velocidade média de cerca de 6 cm/y a noroeste em relação à terra a leste da falha. Los Angeles fica a oeste da falha e, portanto, pode algum dia estar na mesma latitude de São Francisco, que fica a leste da falha. Até que ponto no futuro isso ocorrerá se o deslocamento a ser feito for 590 km a noroeste, supondo que o movimento permaneça constante?
37. Em 26 de maio de 1934, um trem a diesel simplificado de aço inoxidável chamado Zephyr estabeleceu o recorde mundial de velocidade ininterrupta de longa distância para trens. Sua viagem de Denver a Chicago levou 13 horas, 4 minutos e 58 segundos e foi testemunhada por mais de um milhão de pessoas ao longo da rota. A distância total percorrida foi de 1633,8 km. Qual foi sua velocidade média em km/h e m/s?
Solução
\(\displaystyle 34.689 m/s=124.88 km/h\)
38. O atrito das marés está diminuindo a rotação da Terra. Como resultado, a órbita da Lua está aumentando em raio a uma taxa de aproximadamente 4 cm/ano. Supondo que seja uma taxa constante, quantos anos passarão até que o raio da órbita da Lua aumente em\(\displaystyle 3.84×10^6m\) (1%)?
39. Uma estudante dirigiu até a universidade de sua casa e notou que a leitura do odômetro de seu carro aumentou em 12,0 km. A viagem durou 18,0 min.
(a) Qual era a velocidade média dela?
(b) Se a distância em linha reta de sua casa até a universidade for de 10,3 km na direção\(\displaystyle 25.0º\) sul do leste, qual era sua velocidade média?
(c) Se ela voltasse para casa pelo mesmo caminho 7 h 30 minutos depois de sair, quais foram suas médias de velocidade e velocidade durante toda a viagem?
Solução
(a)\(\displaystyle 40.0 km/h\)
(b) 34,3 km/h,\(\displaystyle 25º\)\(\displaystyle S\) de\(\displaystyle E\).
(c) velocidade média =\(\displaystyle 3.20 km/h,\bar{v}=0\).
40. A velocidade de propagação do potencial de ação (um sinal elétrico) em uma célula nervosa depende (inversamente) do diâmetro do axônio (fibra nervosa). Se a célula nervosa que liga a medula espinhal aos pés tem 1,1 m de comprimento e a velocidade do impulso nervoso é de 18 m/s, quanto tempo o sinal nervoso leva para percorrer essa distância?
41. As conversas
com astronautas na superfície lunar foram caracterizadas por uma espécie de eco em que a voz da pessoa na Terra era tão alta no capacete espacial do astronauta que foi captada pelo microfone do astronauta e transmitida de volta à Terra. É razoável supor que o tempo de eco seja igual ao tempo necessário para que a onda de rádio viaje da Terra à Lua e de volta (ou seja, negligenciando qualquer atraso temporal no equipamento eletrônico). Calcule a distância da Terra à Lua, considerando que o tempo de eco foi de 2,56 s e que as ondas de rádio viajam à velocidade da luz (\(\displaystyle 3.00×10^8m/s\))
Solução
384.000 km
42. Um quarterback de futebol corre 15,0 m direto pelo campo de jogo em 2,50 s. Ele é então atingido e empurrado 3,00 m direto para trás em 1,75 s. Ele quebra o tackle e corre direto para frente outros 21,0 m em 5,20 s. Calcule sua velocidade média
(a) para cada um dos três intervalos e
(b) para toda a moção.
43. O modelo planetário do átomo mostra elétrons orbitando o núcleo atômico da mesma forma que planetas orbitam o Sol. Neste modelo, você pode ver o hidrogênio, o átomo mais simples, como tendo um único elétron em uma órbita\(\displaystyle 1.06×10^{−10}m\) circular de diâmetro.
(a) Se a velocidade média do elétron nesta órbita for conhecida\(\displaystyle 2.20×10^6m/s\), calcule o número de revoluções por segundo que ele faz em torno do núcleo.
(b) Qual é a velocidade média do elétron?
Solução
(a)\(\displaystyle 6.61×10^{15}rev/s\)
(b) 0 m/s
2.4: Aceleração
44. Uma chita pode acelerar do repouso a uma velocidade de 30,0 m/s em 7,00 s. Qual é sua aceleração?
Solução
\(\displaystyle 4.29m/s^2\)
45. Aplicação profissional
O Dr. John Paul Stapp foi oficial da Força Aérea dos EUA que estudou os efeitos da desaceleração extrema no corpo humano. Em 10 de dezembro de 1954, Stapp pilotou um foguete de trenó, acelerando do repouso até uma velocidade máxima de 282 m/s (1015 km/h) em 5,00 s, e foi trazida de volta ao descanso em apenas 1,40 s! Calcule sua (a) aceleração e (b) desaceleração. Expresse cada um em múltiplos\(\displaystyle g (9.80 m/s^2)\) de considerando sua relação com a aceleração da gravidade.
46. Uma viajante tira o carro da garagem com uma aceleração de\(\displaystyle 1.40 m/s^2\)
(a) Quanto tempo ela leva para atingir uma velocidade de 2,00 m/s?
(b) Se ela então frear até parar em 0,800 s, qual é a desaceleração dela?
Solução
(a)\(\displaystyle 1.43 s\)
(b)\(\displaystyle −2.50m/s^2\)
47. Suponha que um míssil balístico intercontinental vá do repouso a uma velocidade suborbital de 6,50 km/s em 60,0 s (a velocidade e o tempo reais são classificados). Qual é sua aceleração média em\(\displaystyle m/s^2\) e em múltiplos de\(\displaystyle g (9.80 m/s^2)\)?
2.5: Equações de movimento para aceleração constante em uma dimensão
48. Um velocista de classe olímpica inicia uma corrida com uma aceleração de\(\displaystyle 4.50 m/s^2\)
(a) Qual é a velocidade dela 2,40 s depois?
(b) Esboce um gráfico de sua posição versus tempo para esse período.
Solução
(a)\(\displaystyle 10.8m/s\)
(b)
49. Uma bola bem lançada é presa em uma luva bem acolchoada. Se a desaceleração da bola for\(\displaystyle 2.10×10^4m/s^2\) de 1,85 ms\(\displaystyle (1 ms=10^{−3}s)\) desde o momento em que a bola toca pela primeira vez na luva até que ela pare, qual foi a velocidade inicial da bola?
Solução
38,9 m/s (cerca de 87 milhas por hora)
50. Uma bala em uma arma é acelerada da câmara de disparo até o final do cano a uma taxa média de\(\displaystyle 6.20×10^5m/s^2\) para\(\displaystyle 8.10×10^{−4}s\). Qual é a velocidade do focinho (ou seja, sua velocidade final)?
51. (a) Um trem suburbano leve acelera a uma taxa de\(\displaystyle 1.35 m/s^2\). Quanto tempo é necessário para atingir a velocidade máxima de 80,0 km/h, partindo do repouso?
(b) O mesmo trem normalmente desacelera a uma taxa de\(\displaystyle 1.65 m/s^2\). Quanto tempo leva para parar de sua velocidade máxima?
(c) Em emergências, o trem pode desacelerar mais rapidamente, parando de 80,0 km/h em 8,30 s. Em que consiste sua desaceleração de emergência\(\displaystyle m/s^2\)?
Solução
(a)\(\displaystyle 16.5 s\)
(b)\(\displaystyle 13.5 s\)
(c)\(\displaystyle −2.68 m/s^2\)
52. Ao entrar em uma rodovia, um carro acelera do repouso a uma taxa\(\displaystyle 2.40 m/s^2\) de 12,0 s.
(a) Faça um esboço da situação.
(b) Liste os conhecidos neste problema.
(c) Até onde o carro viaja nesses 12,0 s? Para resolver essa parte, primeiro identifique o desconhecido e depois discuta como você escolheu a equação apropriada para resolvê-lo. Depois de escolher a equação, mostre suas etapas para resolver o desconhecido, verifique suas unidades e discuta se a resposta é razoável.
(d) Qual é a velocidade final do carro? Resolva esse desconhecido da mesma maneira que na parte (c), mostrando todas as etapas explicitamente.
53. No final de uma corrida, um corredor desacelera de uma velocidade de 9,00 m/s a uma taxa de\(\displaystyle 2.00 m/s^2\).
(a) Até onde ela viaja nos próximos 5,00 s?
(b) Qual é a velocidade final dela?
(c) Avalie o resultado. Isso faz sentido?
Solução
(a)\(\displaystyle 20.0 m\)
(b)\(\displaystyle −1.00 m/s\)
(c) Esse resultado realmente não faz sentido. Se a corredora começar a 9,00 m/s e desacelerar\(\displaystyle 2.00 m/s^2\), ela terá parado após 4,50 s. Se continuar desacelerando, estará correndo para trás.
54. Aplicação profissional:
O sangue é acelerado do repouso para 30,0 cm/s a uma distância de 1,80 cm pelo ventrículo esquerdo do coração.
(a) Faça um esboço da situação.
(b) Liste os conhecidos neste problema.
(c) Quanto tempo demora a aceleração? Para resolver essa parte, primeiro identifique o desconhecido e depois discuta como você escolheu a equação apropriada para resolvê-lo. Depois de escolher a equação, mostre seus passos para resolver o desconhecido, verificando suas unidades.
(d) A resposta é razoável quando comparada com o tempo de um batimento cardíaco?
55. Em um tapa, um jogador de hóquei acelera o disco de uma velocidade de 8,00 m/s para 40,0 m/s na mesma direção. Se essa foto for tirada\(\displaystyle 3.33×10^{−2}s\), calcule a distância na qual o disco acelera.
Solução
0,799 m
56. Uma motocicleta potente pode acelerar do repouso até 26,8 m/s (100 km/h) em apenas 3,90 s.
(a) Qual é sua aceleração média?
(b) Até onde ele viaja nesse período?
57. Os trens de carga podem produzir apenas acelerações e desacelerações relativamente pequenas.
(a) Qual é a velocidade final de um trem de carga que acelera a uma taxa\(\displaystyle 0.0500 m/s^2\) de 8,00 min, começando com uma velocidade inicial de 4,00 m/s?
(b) Se o trem puder desacelerar a uma taxa de\(\displaystyle 0.550 m/s^2\), quanto tempo levará para parar nessa velocidade?
(c) Até onde ele viajará em cada caso?
Solução
(a)\(\displaystyle 28.0 m/s\)
(b)\(\displaystyle 50.9 s\)
(c) 7,68 km para acelerar e 713 m para desacelerar
58. Um projétil de fogos de artifício é acelerado do repouso até uma velocidade de 65,0 m/s em uma distância de 0,250 m.
(a) Quanto tempo durou a aceleração?
(b) Calcule a aceleração.
59. Um cisne em um lago voa batendo as asas e correndo sobre a água.
(a) Se o cisne atingir uma velocidade de 6,00 m/s para decolar e acelerar do repouso a uma taxa média de\(\displaystyle 0.350 m/s^2\), até onde ele viajará antes de voar?
(b) Quanto tempo isso leva?
Solução
(a)\(\displaystyle 51.4m\)
(b)\(\displaystyle 17.1 s\)
60. Aplicação profissional:
O cérebro de um pica-pau é especialmente protegido de grandes desacelerações por fixações semelhantes a tendões dentro do crânio. Ao bicar uma árvore, a cabeça do pica-pau para a partir de uma velocidade inicial de 0,600 m/s a uma distância de apenas 2,00 mm.
(a) Encontre a aceleração em\(\displaystyle m/s^2\) e em múltiplos de\(\displaystyle g(g=9.80m/s^2)\).
(b) Calcule o tempo de parada.
(c) Os tendões que envolvem o cérebro se estendem, fazendo com que sua distância de parada seja 4,50 mm (maior que a cabeça e, portanto, menor desaceleração do cérebro). O que é a desaceleração do cérebro, expressa em múltiplos de\(\displaystyle g\)?
61. Um jogador de futebol incerto colide com um poste acolchoado enquanto corre a uma velocidade de 7,50 m/s e pára completamente depois de comprimir o acolchoamento e seu corpo 0,350 m.
(a) Qual é a desaceleração dele?
(b) Quanto tempo dura a colisão?
Solução
(a)\(\displaystyle −80.4m/s^2\)
(b)\(\displaystyle 9.33×10^{−2}s\)
62. Na Segunda Guerra Mundial, houve vários casos relatados de aviadores que pularam de seus aviões flamejantes sem paraquedas para escapar da morte certa. Alguns caíram cerca de 20.000 pés (6000 m) e alguns deles sobreviveram, com poucos ferimentos fatais. Para esses pilotos sortudos, os galhos das árvores e a neve no solo permitiram que sua desaceleração fosse relativamente pequena. Se assumirmos que a velocidade de um piloto após o impacto foi de 123 mph (54 m/s), então qual foi sua desaceleração? Suponha que as árvores e a neve o pararam a uma distância de 3,0 m.
63. Considere um esquilo cinza caindo de uma árvore no chão.
(a) Se ignorarmos a resistência do ar neste caso (apenas por causa desse problema), determine a velocidade de um esquilo antes de atingir o solo, supondo que ele tenha caído de uma altura de 3,0 m.
(b) Se o esquilo parar a uma distância de 2,0 cm dobrando seus membros, compare sua desaceleração com a do aviador no problema anterior.
Solução
(a)\(\displaystyle 7.7 m/s\)
(b)\(\displaystyle −15×10^2m/s^2\). Isso é cerca de 3 vezes a desaceleração dos pilotos, que estavam caindo de milhares de metros de altura!
64. Um trem expresso passa por uma estação. Ele entra com uma velocidade inicial de 22,0 m/s e desacelera a uma taxa de à\(\displaystyle 0.150 m/s^2\) medida que avança. A estação tem 210 m de comprimento.
(a) Quanto tempo dura o nariz do trem na estação?
(b) Quão rápido é quando o nariz sai da estação?
(c) Se o trem tiver 130 m de comprimento, quando o final do trem sai da estação?
(d) Qual é a velocidade da extremidade do trem quando ele sai?
65. Na verdade, os dragsters podem atingir uma velocidade máxima de 145 m/s em apenas 4,45 — um tempo consideravelmente menor do que o dado em Exemplo e Exemplo.
(a) Calcule a aceleração média para esse dragster.
(b) Encontre a velocidade final desse dragster começando do repouso e acelerando na taxa encontrada em (a) por 402 m (um quarto de milha) sem usar nenhuma informação a tempo.
(c) Por que a velocidade final é maior do que a usada para encontrar a aceleração média?
Dica: Considere se a suposição de aceleração constante é válida para um dragster. Caso contrário, discuta se a aceleração seria maior no início ou no final da corrida e qual efeito isso teria na velocidade final.
Solução
(a)\(\displaystyle 32.6 m/s^2\)
(b)\(\displaystyle 162 m/s\)
(c)\(\displaystyle v>v_{max}\), porque a suposição de aceleração constante não é válida para um dragster. Um dragster muda de marcha e teria uma aceleração maior na primeira marcha do que na segunda marcha do que na terceira marcha, etc. A aceleração seria maior no\(\displaystyle 32.6 m/s^2\) início, então não estaria acelerando nos últimos metros, mas substancialmente menor, e a velocidade final seria menor que 162 m/s.
66. Um ciclista corre no final de uma corrida para conquistar a vitória. O piloto tem uma velocidade inicial de 11,5 m/s e acelera à taxa\(\displaystyle 0.500 m/s^2\) de 7,00 s.
(a) Qual é a velocidade final dele?
(b) O piloto continua nessa velocidade até a linha de chegada. Se ele estava a 300 m da linha de chegada quando começou a acelerar, quanto tempo ele economizou?
(c) Um outro piloto estava 5,00 m à frente quando o vencedor começou a acelerar, mas não conseguiu acelerar e viajou a 11,8 m/s até a linha de chegada. Quão à frente dele (em metros e em segundos) o vencedor terminou?
67. Em 1967, o neozelandês Burt Munro estabeleceu o recorde mundial de uma motocicleta indiana, no Bonneville Salt Flats, em Utah, com uma velocidade máxima de 183,58 mi/h. O percurso de ida e volta tinha 5,00 km de extensão. As taxas de aceleração são frequentemente descritas pelo tempo necessário para atingir 60,0 mi/h de repouso. Se esse tempo foi de 4,00 s e Burt acelerou nesse ritmo até atingir sua velocidade máxima, quanto tempo Burt levou para concluir o percurso?
Solução
104 s
68. (a) Um recorde mundial foi estabelecido para a corrida masculina de 100 m nos Jogos Olímpicos de 2008 em Pequim por Usain Bolt, da Jamaica. Bolt “cruzou” a linha de chegada com um tempo de 9,69 s. Se assumirmos que Bolt acelerou por 3,00 s para atingir sua velocidade máxima e manteve essa velocidade pelo resto da corrida, calcule sua velocidade máxima e sua aceleração.
(b) Durante as mesmas Olimpíadas, Bolt também estabeleceu o recorde mundial na corrida de 200 m com o tempo de 19,30 s. Usando as mesmas suposições da corrida de 100 m, qual foi sua velocidade máxima para esta corrida?
Solução
(a)\(\displaystyle v=12.2 m/s; a=4.07 m/s^2\)
(b)\(\displaystyle v=11.2 m/s\)
2.7: Objetos caindo
Suponha que a resistência do ar seja insignificante, salvo indicação em contrário.
69. Calcule o deslocamento e a velocidade em tempos de
(a) 0,500,
(b) 1,00,
(c) 1,50 e
(d) 2,00 s para uma bola lançada diretamente para cima com uma velocidade inicial de 15,0 m/s. Assuma o ponto de lançamento a ser\(\displaystyle y_0=0\)
Solução
(a)\(\displaystyle y_1=6.28 m; v_1=10.1 m/s\)
(b)\(\displaystyle y_2=10.1 m; v_2=5.20 m/s\)
(c)\(\displaystyle y_3=11.5 m; v_3=0.300 m/s\)
(d)\(\displaystyle y_4=10.4 m; v_4=−4.60 m/s\)
70. Calcule o deslocamento e a velocidade em tempos de
(a) 0,500,
(b) 1,00,
(c) 1,50,
(d) 2,00 e
(e) 2,50 s para uma rocha lançada diretamente para baixo com uma velocidade inicial de 14,0 m/s da Ponte Verrazano Narrows, na cidade de Nova York. A estrada desta ponte está 70,0 m acima da água.
71. Um árbitro de basquete joga a bola diretamente para a dica inicial. A que velocidade um jogador de basquete deve deixar o chão para subir 1,25 m acima do chão na tentativa de pegar a bola?
Solução
\(\displaystyle v_0=4.95 m/s\)
72. Um helicóptero de resgate está pairando sobre uma pessoa cujo barco afundou. Um dos socorristas joga um colete salva-vidas direto para a vítima com uma velocidade inicial de 1,40 m/s e observa que são necessários 1,8 s para chegar à água.
(a) Liste os conhecidos desse problema.
(b) A que altura acima da água o preservador foi liberado? Observe que a corrente descendente do helicóptero reduz os efeitos da resistência do ar na queda do colete salva-vidas, de modo que uma aceleração igual à da gravidade é razoável.
73. Um golfinho em um show aquático salta direto da água a uma velocidade de 13,0 m/s.
(a) Liste os conhecidos desse problema.
(b) A que altura seu corpo se eleva acima da água? Para resolver essa parte, primeiro observe que a velocidade final agora é conhecida e identifique seu valor. Em seguida, identifique o desconhecido e discuta como você escolheu a equação apropriada para resolvê-lo. Depois de escolher a equação, mostre suas etapas para resolver o desconhecido, verificar as unidades e discuta se a resposta é razoável.
(c) Quanto tempo o golfinho fica no ar? Negligencie quaisquer efeitos devido ao seu tamanho ou orientação.
Solução
(a)\(\displaystyle a=−9.80 m/s^2; v_0=13.0 m/s; y_0=0 m\)
(b)\(\displaystyle v=0m/s\). Desconhecida é\(\displaystyle y\) a distância até o topo da trajetória, onde a velocidade é zero. Use a equação\(\displaystyle v^2=v^2_0+2a(y−y_0)\) porque ela contém todos os valores conhecidos\(\displaystyle y\), exceto para, para que possamos resolver\(\displaystyle y\). Resolvendo\(\displaystyle y\) doações
\(\displaystyle v^2−v^2_0=2ay−y_0)\)
\(\displaystyle \frac{v^2−v^2_0}{2a}=y−y_0\)
\(\displaystyle y=y0+\frac{v^2−v^2_0}{2a}=0m+\frac{(0 m/s)^2−(13.0 m/s)^2}{2(−9.80 m/s^2)}=8.62 m\)
Os golfinhos medem cerca de 2 metros de comprimento e podem pular várias vezes seu comprimento para fora da água, então esse é um resultado razoável.
(c)\(\displaystyle 2.65 s\)
74. Um nadador salta direto de uma prancha de mergulho e cai primeiro na piscina. Ela começa com uma velocidade de 4,00 m/s e seu ponto de decolagem está 1,80 m acima da piscina.
(a) Há quanto tempo seus pés estão no ar?
(b) Qual é o ponto mais alto dela acima do tabuleiro?
(c) Qual é a velocidade dela quando seus pés batem na água?
75. (a) Calcule a altura de um penhasco se levar 2,35 s para uma rocha atingir o solo quando é lançada diretamente do penhasco com uma velocidade inicial de 8,00 m/s.
(b) Quanto tempo levaria para chegar ao solo se ele fosse jogado diretamente para baixo com a mesma velocidade?
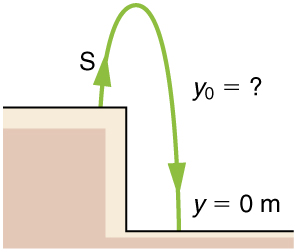
Solução
(a) 8,26 m
(b) 0,717 s
76. Um arremessador muito forte, mas inepto, coloca o tiro na vertical com uma velocidade inicial de 11,0 m/s. Quanto tempo ele tem para sair do caminho se o tiro for lançado a uma altura de 2,20 m e ele tiver 1,80 m de altura?
77. Você joga uma bola para cima com uma velocidade inicial de 15,0 m/s. Ela passa por um galho de árvore no caminho para cima a uma altura de 7,00 m. Quanto tempo adicional passará antes que a bola passe pelo galho da árvore no caminho de volta para baixo?
Solução
1.91 s
78. Um canguru pode pular sobre um objeto com 2,50 m de altura.
(a) Calcule sua velocidade vertical ao sair do solo.
(b) Há quanto tempo está no ar?
79. Parado na base de um dos penhascos do Monte. Arapiles em Victoria, Austrália, um caminhante ouve uma pedra se soltar de uma altura de 105 m. Ele não consegue ver a rocha imediatamente, mas depois o vê, 1,50 s depois.
(a) Quão acima do caminhante está a rocha quando ele pode vê-la?
(b) Quanto tempo ele tem que se mover antes que a pedra atinja sua cabeça?
Solução
(a) 94,0 m
(b) 3,13 s
80. Um objeto é lançado de uma altura de 75,0 m acima do nível do solo.
(a) Determine a distância percorrida durante o primeiro segundo.
(b) Determine a velocidade final na qual o objeto atinge o solo. (c) Determine a distância percorrida durante o último segundo de movimento antes de atingir o solo.
81. Há um penhasco de 250 m de altura no Half Dome, no Parque Nacional de Yosemite, na Califórnia. Suponha que uma pedra se solte do topo desse penhasco.
(a) Quão rápido ele vai passar quando atingir o solo?
(b) Supondo um tempo de reação de 0,300 s, quanto tempo um turista no fundo terá para sair do caminho depois de ouvir o som da rocha se soltando (negligenciando a altura do turista, que se tornaria insignificante de qualquer maneira se fosse atingida)? A velocidade do som é de 335 m/s neste dia.
Solução
(a) -70,0 m/s (para baixo)
(b) 6,10 s
82. Uma bola é lançada diretamente para cima. Ele passa por uma janela de 2,00 m de altura a 7,50 m do chão em seu caminho para cima e leva 0,312 s para passar pela janela. Qual foi a velocidade inicial da bola? Dica: Primeiro, considere apenas a distância ao longo da janela e resolva a velocidade da bola na parte inferior da janela. Em seguida, considere apenas a distância do solo até a parte inferior da janela e resolva a velocidade inicial usando a velocidade na parte inferior da janela como a velocidade final.
83. Suponha que você jogue uma pedra em um poço escuro e, usando equipamento de precisão, meça o tempo até que o som de um respingo retorne.
(a) Negligenciando o tempo necessário para o som subir até o poço, calcule a distância até a água se o som retornar em 2.0000 s.
(b) Agora calcule a distância levando em consideração o tempo de viagem do som até o poço. A velocidade do som é de 332,00 m/s neste poço.
Solução
(a)\(\displaystyle 19.6 m\)
(b)\(\displaystyle 18.5 m\)
84. Uma bola de aço é jogada em um piso duro de uma altura de 1,50 m e se recupera para uma altura de 1,45 m.
(a) Calcule sua velocidade logo antes de atingir o chão.
(b) Calcule sua velocidade logo após sair do chão e voltar para cima.
(c) Calcule sua aceleração durante o contato com o piso se esse contato durar 0,0800 ms\(\displaystyle (8.00×10^{−5}s)\)
(d) Quanto a bola se comprimiu durante sua colisão com o piso, supondo que o piso seja absolutamente rígido?
85. Uma moeda é lançada de um balão de ar quente que está 300 m acima do solo e sobe a 10,0 m/s para cima. Para a moeda, encontre
(a) a altura máxima atingida,
(b) sua posição e velocidade 4,00 s após ser liberado, e
(c) o tempo antes de atingir o solo.
Solução
(a) 305 m
(b) 262 m, -29,2 m/s
(c) 8,91 s
86. Uma bola de tênis macia é jogada em um piso duro de uma altura de 1,50 m e se recupera para uma altura de 1,10 m.
(a) Calcule sua velocidade logo antes de atingir o chão.
(b) Calcule sua velocidade logo após sair do chão e voltar para cima.
(c) Calcule sua aceleração durante o contato com o piso se esse contato durar 3,50 ms\(\displaystyle (3.50×10^{−3}s)\)
(d) Quanto a bola se comprimiu durante sua colisão com o piso, supondo que o piso seja absolutamente rígido?
2.8: Análise gráfica do movimento unidimensional
Nota: Sempre há incerteza nos números retirados dos gráficos. Se suas respostas forem diferentes dos valores esperados, examine-as para ver se elas estão dentro das incertezas de extração de dados estimadas por você.
87. (a) Tomando a inclinação da curva na Figura, verifique se a velocidade do carro a jato é de 115 m/s em\(\displaystyle t=20\) s.
(b) Ao tomar a inclinação da curva em qualquer ponto da Figura, verifique se a aceleração do carro a jato é\(\displaystyle 5.0 m/s^2\)
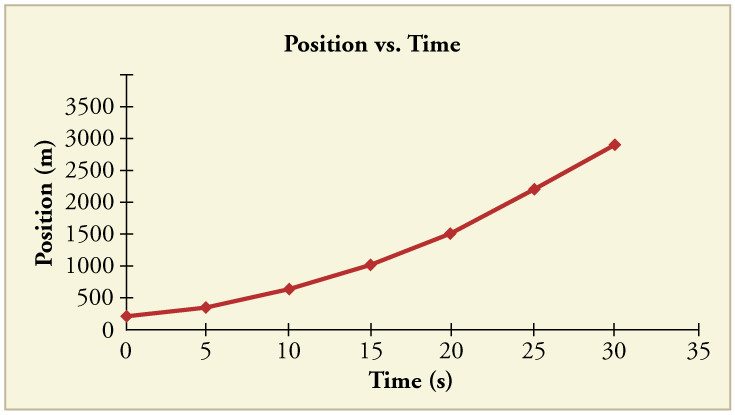
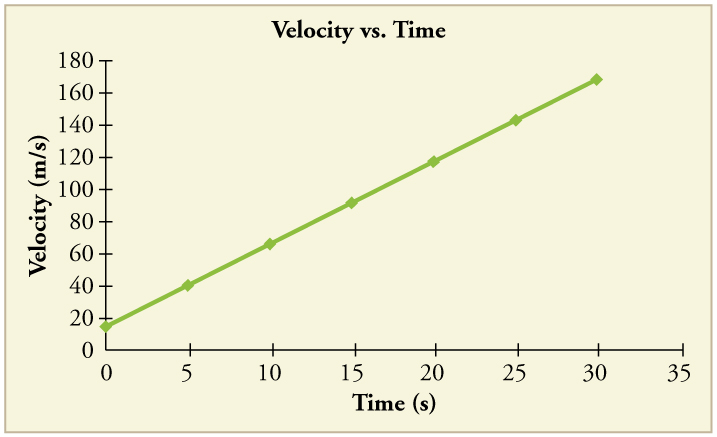
Solução
(a)\(\displaystyle 115 m/s\)
(b)\(\displaystyle 5.0 m/s^2\)
88. Usando valores aproximados, calcule a inclinação da curva na Figura para verificar se a velocidade em\(\displaystyle t=10.0 s\) é de 0,208 m/s. Suponha que todos os valores sejam conhecidos por 3 números significativos.
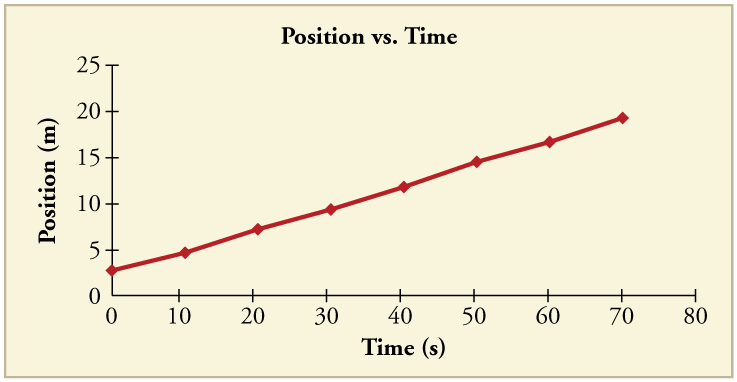
89. Usando valores aproximados, calcule a inclinação da curva na Figura acima para verificar se a velocidade em\(\displaystyle t=30.0 s\) é de aproximadamente 0,24 m/s.
Solução
\(\displaystyle v=\frac{(11.7−6.95)×10^3m}{(40.0 – 20.0)s}=238 m/s\)
90. Ao tomar a inclinação da curva na Figura, verifique se a aceleração está\(\displaystyle 3.2 m/s^2\) em\(\displaystyle t=10 s\)
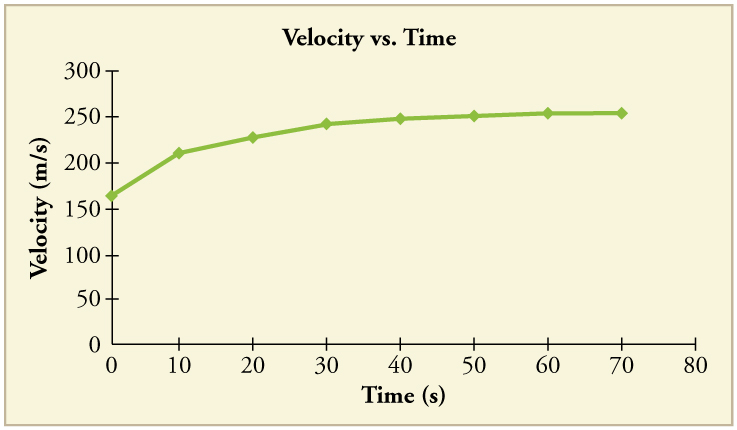
91. Construa o gráfico de posição do trem de transporte do metrô conforme mostrado em [link] (a). Seu gráfico deve mostrar a posição do trem, em quilômetros, de t = 0 a 20 s. Você precisará usar as informações sobre aceleração e velocidade dadas nos exemplos desta figura.
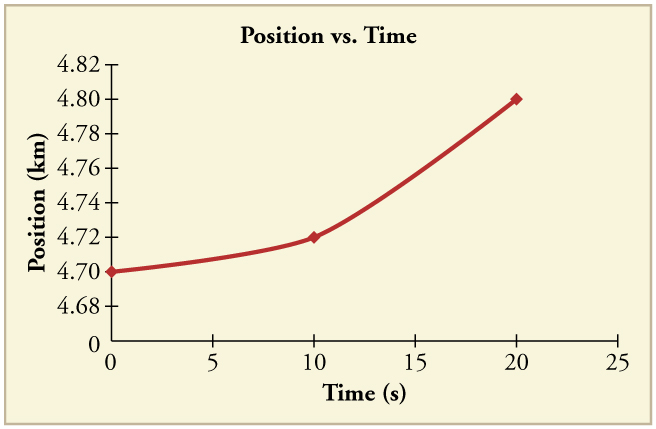
92. (a) Pegue a inclinação da curva na Figura para encontrar a velocidade do corredor em\(\displaystyle t=2.5 s\).
(b) Repita em 7,5 s. Esses valores devem ser consistentes com o gráfico na Figura.
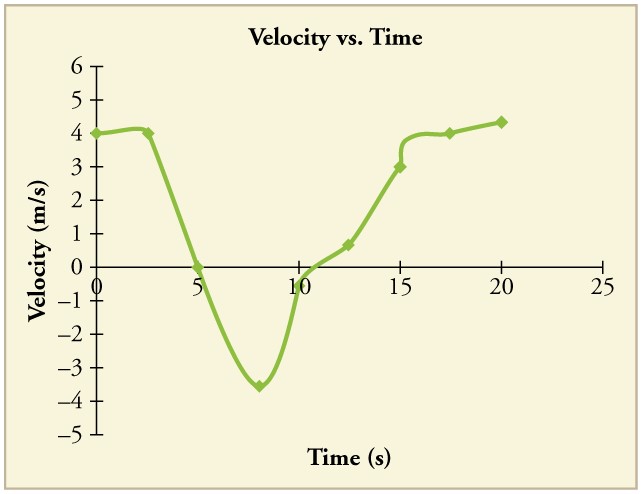
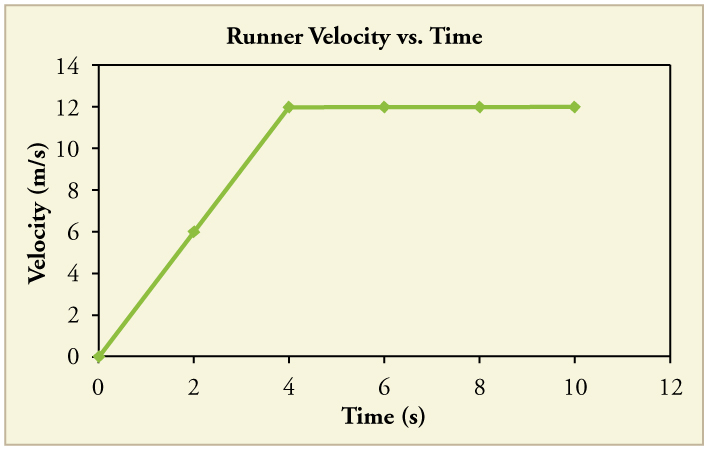
93. Um gráfico de\(\displaystyle v(t)\) é mostrado para um velocista de pista de classe mundial em uma corrida de 100 m. (Veja a Figura).
(a) Qual é a velocidade média dele nos primeiros 4 s?
(b) Qual é a velocidade instantânea dele\(\displaystyle t=5 s\)?
(c) Qual é a aceleração média dele entre 0 e 4 s?
(d) Qual é o tempo dele para a corrida?
Solução
(a)\(\displaystyle 6 m/s\)
(b)\(\displaystyle 12 m/s\)
(c)\(\displaystyle 3 m/s^2\)
(d)\(\displaystyle 10 s\)
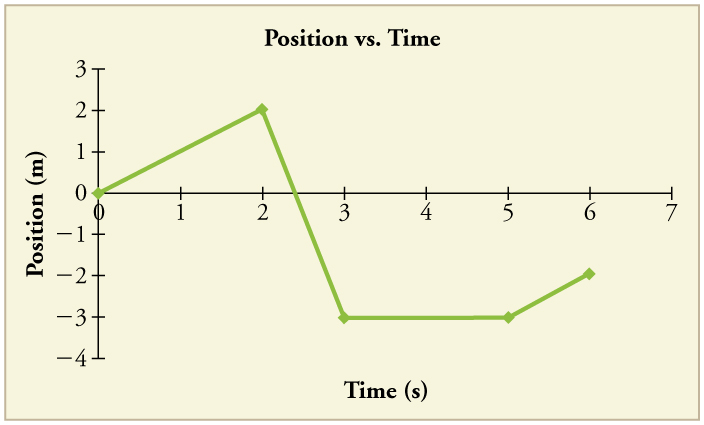
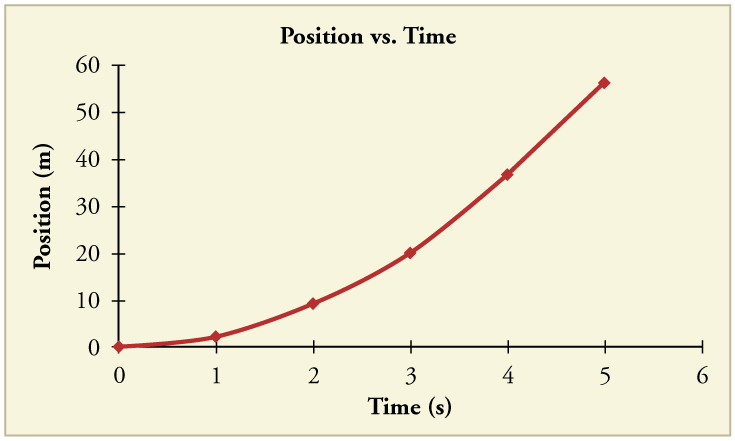
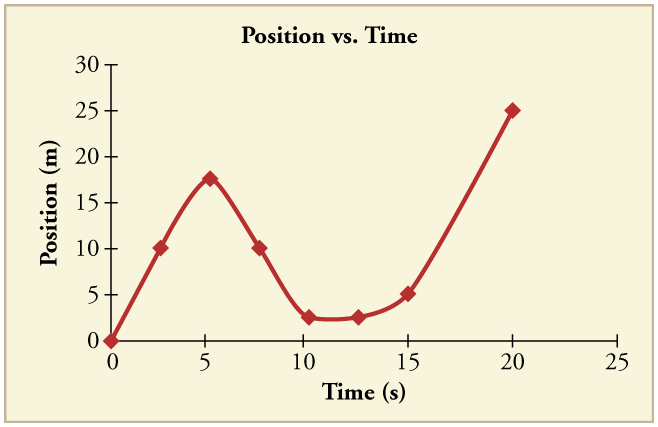
94. A figura mostra o gráfico de posição de uma partícula por 6 s.
(a) Desenhe o gráfico de Velocidade versus Tempo correspondente.
(b) Qual é a aceleração entre 0 s e 2 s?
(c) O que acontece com a aceleração em exatamente 2 s?