Skip to main content
Global

2.8: Análise gráfica do movimento unidimensional

  1. Last updated
  2. Save as PDF
  • Page ID
    194284

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Descreva um gráfico em linha reta em termos de sua inclinação e intercepto y.
    • Determine a velocidade média ou a velocidade instantânea a partir de um gráfico de posição versus tempo.
    • Determine a aceleração média ou instantânea a partir de um gráfico de velocidade versus tempo.
    • Derive um gráfico de velocidade versus tempo a partir de um gráfico de posição versus tempo.
    • Derive um gráfico de aceleração versus tempo a partir de um gráfico de velocidade versus tempo.

    Um gráfico, como uma imagem, vale mais que mil palavras. Os gráficos não contêm apenas informações numéricas; eles também revelam relações entre quantidades físicas. Esta seção usa gráficos de deslocamento, velocidade e aceleração versus tempo para ilustrar a cinemática unidimensional.

    Inclinações e relações gerais

    Primeiro, observe que os gráficos neste texto têm eixos perpendiculares, um horizontal e outro vertical. Quando duas quantidades físicas são plotadas uma contra a outra em tal gráfico, o eixo horizontal é geralmente considerado uma variável independente e o eixo vertical uma variável dependente. Se chamarmos o eixo horizontal de eixo x e o eixo vertical de eixo y, como na Figura\(\PageIndex{1}\), um gráfico em linha reta tem a forma geral

    \[y=mx+b.\]

    Aqui\(m\) está a inclinação, definida como sendo a subida dividida pelo trajeto da linha reta (Figura\(\PageIndex{1}\)). A letra\(b\) é usada para interceptar y, que é o ponto em que a linha cruza o eixo vertical.

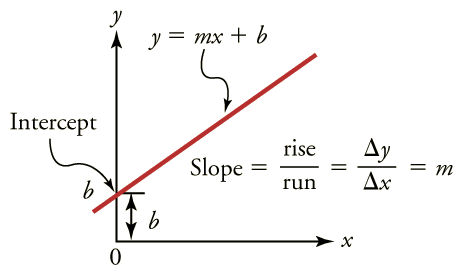
    Gráfico de uma linha reta inclinada para cima em cerca de 40 graus.
    Figura\(\PageIndex{1}\): Um gráfico em linha reta. A equação para uma linha reta é\(y=mx+b\).

    Gráfico de deslocamento versus tempo (a = 0, então v é constante)

    O tempo geralmente é uma variável independente da qual outras quantidades, como o deslocamento, dependem. Um gráfico do deslocamento versus tempo teria, portanto, no eixo vertical e no eixo horizontal. A figura\(\PageIndex{2}\) é exatamente um gráfico em linha reta. Ele mostra um gráfico do deslocamento em relação ao tempo de um carro movido a jato em um leito de lago muito plano e seco em Nevada.

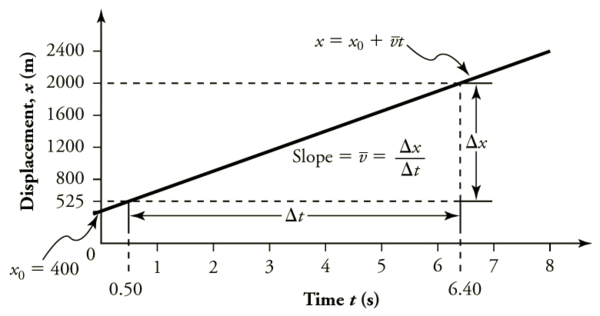
    Gráfico de linha da posição do carro a jato em metros versus tempo em segundos. A linha é reta com uma inclinação positiva. O intercepto y é de quatrocentos metros. A mudança total no tempo é de oito pontos e zero segundos. A posição inicial é de quatrocentos metros. A posição final é de dois mil metros.
    Figura\(\PageIndex{2}\): Gráfico do deslocamento em relação ao tempo de um carro movido a jato no Bonneville Salt Flats.

    Usando a relação entre variáveis dependentes e independentes, vemos que a inclinação no gráfico acima é a velocidade média\(\bar{v}\) e o intercepto é o deslocamento no tempo zero, ou seja,\(x_0\). Substituindo esses símbolos em\(y=mx+b\) dá

    \[x=\bar{v}t+x_0\]

    ou

    \[x=x_0+ \bar{v}t.\]

    Assim, um gráfico de deslocamento versus tempo fornece uma relação geral entre deslocamento, velocidade e tempo, além de fornecer informações numéricas detalhadas sobre uma situação específica.

    A INCLINAÇÃO DO\(X\) VS. \(T\)

    A inclinação do gráfico do deslocamento\(x\) versus tempo\(t\) é a velocidade\(v\).

    \(\displaystyle slope=\frac{Δx}{Δt}=v\)

    Observe que essa equação é a mesma derivada algebricamente de outras equações de movimento em Equações de movimento para aceleração constante em uma dimensão.

    A partir da figura, podemos ver que o carro tem um deslocamento de 25 m a 0,50 s e 2000 m a 6,40 s. Seu deslocamento em outros momentos pode ser lido no gráfico; além disso, informações sobre sua velocidade e aceleração também podem ser obtidas no gráfico.

    Exemplo\(\PageIndex{1}\):Determining Average Velocity from a Graph of Displacement versus Time: Jet Car

    Encontre a velocidade média do carro cuja posição está representada graficamente na Figura\(\PageIndex{2}\).

    Estratégia

    A inclinação de um gráfico de\(x\) vs.\(t\) é a velocidade média, já que a inclinação é igual à elevação ao longo da corrida. Nesse caso, aumento = mudança de posição e corrida = mudança no tempo, de modo que

    \[\displaystyle slope=\frac{Δx}{Δt}=\bar{v}. \nonumber\]

    Como a inclinação é constante aqui, quaisquer dois pontos no gráfico podem ser usados para encontrar a inclinação. (De um modo geral, é mais preciso usar dois pontos amplamente separados na linha reta. Isso ocorre porque qualquer erro na leitura de dados do gráfico é proporcionalmente menor se o intervalo for maior.)

    Solução

    1. Escolha dois pontos na linha. Nesse caso, escolhemos os pontos rotulados no gráfico: (6,4 s, 2000 m) e (0,50 s, 525 m). (Observe, no entanto, que você pode escolher quaisquer dois pontos.)
    2. Substitua os valores x e t dos pontos escolhidos na equação. Lembre-se de que, ao calcular a mudança (Δ), sempre usamos o valor final menos o valor inicial. \[\displaystyle \bar{v}=\frac{Δx}{Δt}=\frac{2000 m−525 m}{6.4 s−0.50 s}, \nonumber\]produzindo\[\displaystyle v−=250 m/s. \nonumber\]

    Discussão

    Esta é uma velocidade terrestre impressionantemente grande (900 km/h, ou cerca de 560 mi/h): muito maior do que o limite de velocidade típico da rodovia de 60 mi/h (27 m/s ou 96 km/h), mas consideravelmente abaixo do recorde de 343 m/s (1234 km/h ou 766 mi/h) estabelecido em 1997.

    Gráficos de movimento quando é constante, mas ≠ 0

    Os gráficos na Figura\(\PageIndex{3}\) abaixo representam o movimento do carro movido a jato à medida que ele acelera em direção à sua velocidade máxima, mas somente durante o período em que sua aceleração é constante. O tempo começa em zero para esse movimento (como se fosse medido com um cronômetro), e o deslocamento e a velocidade são inicialmente de 200 m e 15 m/s, respectivamente.

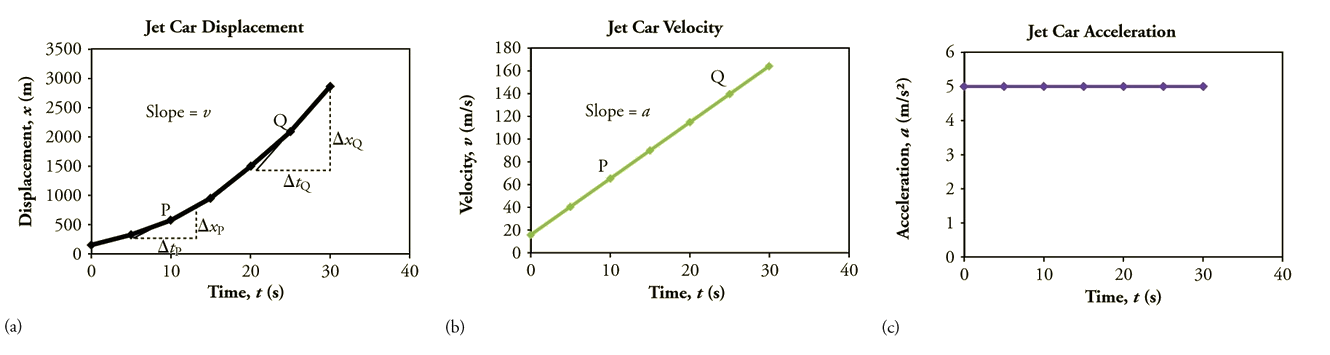
    Gráficos de três linhas. O primeiro é um gráfico linear do deslocamento ao longo do tempo. A linha tem uma inclinação positiva que aumenta com o tempo. O gráfico de segunda linha mostra a velocidade ao longo do tempo. A linha é reta com uma inclinação positiva. O gráfico da terceira linha é de aceleração ao longo do tempo. A linha é reta e horizontal, indicando aceleração constante.

    Figura\(\displaystyle \PageIndex{3}\): Gráficos do movimento de um carro movido a jato durante o período em que sua aceleração é constante. (a) A inclinação de um\(\displaystyle t\) gráfico\(\displaystyle x\) versus é a velocidade. Isso é mostrado em dois pontos, e as velocidades instantâneas obtidas são plotadas no próximo gráfico. A velocidade instantânea em qualquer ponto é a inclinação da tangente nesse ponto. (b) A inclinação do\(\displaystyle t\) gráfico\(\displaystyle v\) vs. é constante para essa parte do movimento, indicando aceleração constante. (c) A aceleração tem o valor constante de\(\displaystyle 5.0 m/s^2\) ao longo do intervalo de tempo traçado.

    Figure_02_07_03a.jpg
    Figura\(\displaystyle \PageIndex{4}\): Um carro a jato da Força Aérea dos EUA acelera em uma pista. (crédito: Matt Trostle, Flickr)

    O gráfico do deslocamento em relação ao tempo na Figura\(\PageIndex{3a}\) é uma curva em vez de uma linha reta. A inclinação da curva se torna mais acentuada à medida que o tempo avança, mostrando que a velocidade está aumentando com o tempo. A inclinação em qualquer ponto em um gráfico de deslocamento versus tempo é a velocidade instantânea nesse ponto. É encontrado desenhando uma linha reta tangente à curva no ponto de interesse e tomando a inclinação dessa linha reta. As linhas tangentes são mostradas para dois pontos na Figura\(\PageIndex{3a}\). Se isso for feito em todos os pontos da curva e os valores forem plotados em relação ao tempo, o gráfico de velocidade versus tempo mostrado na Figura será\(\PageIndex{3b}\) obtido. Além disso, a inclinação do gráfico da velocidade em relação ao tempo é a aceleração, mostrada na Figura\(\PageIndex{3c}\).

    Exemplo\(\PageIndex{2}\):

    Calcule a velocidade do carro a jato em um tempo de 25 s encontrando a inclinação do gráfico\ (\ displaystyle versus\ (\ displaystyle) no gráfico abaixo

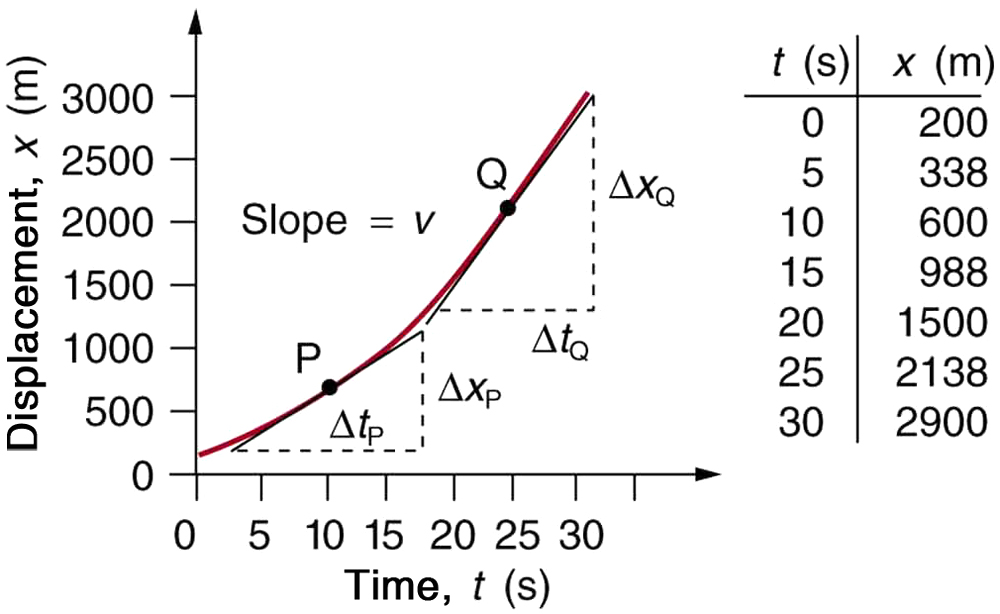
    Um gráfico do deslocamento em relação ao tempo de um carro a jato. O eixo x do tempo vai de zero a trinta e cinco segundos. O eixo y para deslocamento vai de zero a três mil metros. A curva representando o deslocamento é côncava para cima. A inclinação da curva aumenta com o tempo. A inclinação é igual à velocidade v. Existem dois pontos na curva, denominados P e Q. P está localizado no tempo igual a dez segundos. Q está localizado e o tempo é igual a vinte e cinco segundos. Uma linha tangente a P em dez segundos é desenhada e tem uma inclinação delta x sub P sobre delta t sub p. Uma linha tangente a Q em vinte e cinco segundos é desenhada e tem uma inclinação igual a delta x sub q sobre delta t sub q. As coordenadas selecionadas são fornecidas em uma tabela e consistem no seguinte: tempo zero segundos deslocamento dois cem metros; tempo cinco segundos de deslocamento trezentos e trinta e oito metros; tempo dez segundos de deslocamento seiscentos metros; tempo quinze segundos de deslocamento novecentos e oitenta e oito metros. Tempo vinte segundos de deslocamento de mil e quinhentos metros; tempo vinte e cinco segundos de deslocamento de dois mil cento e trinta e oito metros; tempo trinta segundos de deslocamento de dois mil e novecentos metros.
    Figura\(\displaystyle \PageIndex{5}\): A inclinação de um gráfico\ (vs.\) é a velocidade. Isso é mostrado em dois pontos. A velocidade instantânea em qualquer ponto é a inclinação da tangente nesse ponto.

    Estratégia

    A inclinação de uma curva em um ponto é igual à inclinação de uma linha reta tangente à curva nesse ponto. Esse princípio é ilustrado na Figura, onde Q é o ponto em\(\displaystyle t=25 s\).

    Solução

    1. Encontre a linha tangente à curva em\(\displaystyle t=25 s\).
    2. Determine os pontos finais da tangente. Eles correspondem a uma posição de 1300 m no tempo 19 s e a uma posição de 3120 m no tempo 32 s.
    3. Insira esses pontos finais na equação para resolver a inclinação,.

    \(\displaystyle slope=v_Q=\frac{Δx_Q}{Δt_Q}=\frac{(3120 m−1300 m)}{(32 s−19 s)}\)

    Assim,

    \(\displaystyle v_Q=\frac{1820 m}{13 s}=140 m/s.\)

    Discussão

    Este é o valor dado na tabela desta figura para v at\(\displaystyle t=25 s\). O valor de 140 m/s para\(\displaystyle v_Q\) é plotado na Figura. O gráfico completo de\(\displaystyle v\) vs.\(\displaystyle t\) pode ser obtido dessa forma.

    Levando isso um passo adiante, notamos que a inclinação de um gráfico de velocidade versus tempo é aceleração. A inclinação é a elevação dividida pela corrida; em um\(\displaystyle t\) gráfico\(\displaystyle v\) versus, aumento = mudança na velocidade\(\displaystyle Δv\) e corrida = mudança no tempo\(\displaystyle Δt\).

    A INCLINAÇÃO DE V VS. T

    A inclinação de um gráfico de velocidade\(\displaystyle v\) versus tempo\(\displaystyle t\) é aceleração\(\displaystyle a\).

    \(\displaystyle slope=\frac{Δv}{Δt}=a\)

    Como o gráfico de velocidade versus tempo na Figura\(\PageIndex{3b}\) é uma linha reta, sua inclinação é a mesma em todos os lugares, o que implica que a aceleração é constante. A aceleração versus tempo é representada graficamente na Figura (c).

    Informações gerais adicionais podem ser obtidas na Figura e na expressão para uma linha reta,\(\displaystyle y=mx+b.\)

    Nesse caso, o eixo vertical\(\displaystyle y\) é\(\displaystyle V\), o intercepto\(\displaystyle b\) é\(\displaystyle v_0\), a inclinação\(\displaystyle m\) é\(\displaystyle a\) e o eixo horizontal\(\displaystyle x\) é\(\displaystyle t\). Substituir esses símbolos rende

    \[v=v_0+at. \nonumber\]

    Uma relação geral de velocidade, aceleração e tempo foi novamente obtida de um gráfico. Observe que essa equação também foi derivada algebricamente de outras equações de movimento em Equações de movimento para aceleração constante em uma dimensão.

    Não é por acaso que as mesmas equações sejam obtidas por análise gráfica e por técnicas algébricas. De fato, uma maneira importante de descobrir relações físicas é medir várias quantidades físicas e, em seguida, fazer gráficos de uma quantidade em relação a outra para ver se elas estão correlacionadas de alguma forma. As correlações implicam relações físicas e podem ser mostradas por gráficos suaves, como os acima. A partir desses gráficos, as relações matemáticas às vezes podem ser postuladas. Outros experimentos são então realizados para determinar a validade das relações hipotéticas.

    Gráficos de movimento em que a aceleração não é constante

    Agora, considere o movimento do carro a jato à medida que ele vai de 165 m/s até sua velocidade máxima de 250 m/s, representada graficamente na Figura\(\PageIndex{6}\). O tempo novamente começa em zero, e a posição inicial e a velocidade são 2900 m e 165 m/s, respectivamente. (Essas eram a posição final e a velocidade do carro no movimento representado na Figura\(\PageIndex{4}\)) A aceleração diminui gradualmente de\(\displaystyle 5.0 m/s^2\) zero quando o carro atinge 250 m/s. A inclinação do\(\displaystyle t\) gráfico\(\displaystyle x\) vs. aumenta até\(\displaystyle t=55 s\), após o qual a inclinação é constante. Da mesma forma, a velocidade aumenta até 55 s e depois se torna constante, já que a aceleração diminui para zero a 55 s e permanece zero depois.

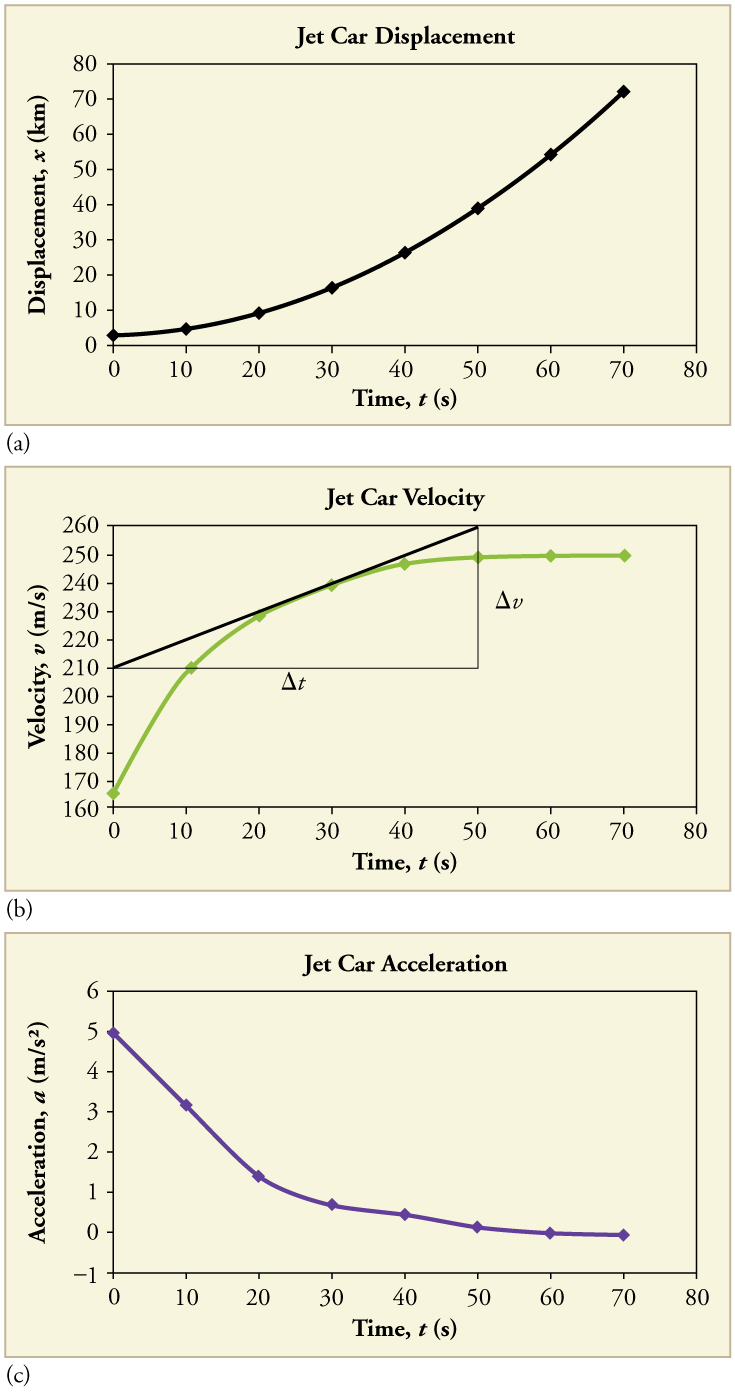
    Gráficos de três linhas do deslocamento, velocidade e aceleração dos carros a jato, respectivamente. O gráfico da primeira linha está posicionado ao longo do tempo. A linha é reta com uma inclinação positiva. O gráfico de segunda linha mostra a velocidade ao longo do tempo. O gráfico de linhas tem uma inclinação positiva que diminui com o tempo e se achata no final. O gráfico da terceira linha é de aceleração ao longo do tempo. A linha tem uma inclinação negativa que aumenta com o tempo até se achatar no final. A linha não é suave, mas tem várias dobras.
    A figura\(\displaystyle \PageIndex{3}\) termina. (a) A inclinação desse gráfico é a velocidade; ela é plotada no próximo gráfico. (b) A velocidade gradualmente se aproxima de seu valor máximo. A inclinação desse gráfico é aceleração; ela é plotada no gráfico final. (c) A aceleração diminui gradualmente para zero quando a velocidade se torna constante.

    Exemplo\(\PageIndex{3}\):Calculating Acceleration from a Graph of Velocity versus Time

    Calcule a aceleração do carro a jato em um tempo de 25 s encontrando a inclinação do\(\displaystyle t\) gráfico\(\displaystyle v\) vs. na Figura\(\PageIndex{6b}\).

    Estratégia

    A inclinação da curva em\(\displaystyle t=25 s\) é igual à inclinação da reta tangente nesse ponto, conforme ilustrado na Figura\(\PageIndex{6b}\).

    Solução

    Determine os pontos finais da reta tangente a partir da figura e, em seguida, conecte-os à equação para resolver a inclinação,.

    \(\displaystyle slope=\frac{Δv}{Δt}=\frac{(260 m/s−210 m/s)}{(51 s−1.0 s)}\)
    \(\displaystyle a=\frac{50 m/s}{50 s}=1.0 m/s^2.\)

    Discussão

    Observe que esse valor para a é consistente com o valor plotado na Figura (c) em\(\displaystyle t=25 s\).

    Um gráfico de deslocamento versus tempo pode ser usado para gerar um gráfico de velocidade versus tempo, e um gráfico de velocidade versus tempo pode ser usado para gerar um gráfico de aceleração versus tempo. Fazemos isso encontrando a inclinação dos gráficos em cada ponto. Se o gráfico for linear (ou seja, uma linha com uma inclinação constante), é fácil encontrar a inclinação em qualquer ponto e você tem a inclinação para cada ponto. A análise gráfica do movimento pode ser usada para descrever características específicas e gerais da cinemática. Os gráficos também podem ser usados para outros tópicos de física. Um aspecto importante da exploração de relacionamentos físicos é representá-los graficamente e procurar relacionamentos subjacentes.

    Exercício\(\displaystyle \PageIndex{1}\):Check Your Understanding

    Um gráfico da velocidade versus tempo de um navio entrando em um porto é mostrado abaixo.

    1. Descreva o movimento do navio com base no gráfico.
    2. Como seria um gráfico da aceleração da nave?
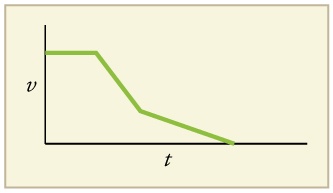
    Gráfico de linha da velocidade versus tempo. A linha tem três pernas. A primeira perna é plana. A segunda perna tem uma inclinação negativa. A terceira perna também tem uma inclinação negativa, mas a inclinação não é tão negativa quanto a segunda perna.
    Figura\(\displaystyle \PageIndex{7}\)
    Responda a

    (a) A nave se move a uma velocidade constante e, em seguida, começa a desacelerar a uma taxa constante. Em algum momento, sua taxa de desaceleração diminui. Ele mantém essa taxa de desaceleração mais baixa até parar de se mover.

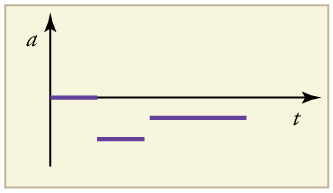
    Solução b

    Um gráfico de aceleração versus tempo mostraria aceleração zero na primeira etapa, aceleração negativa grande e constante na segunda etapa e aceleração negativa constante.

    Um gráfico de linha de aceleração versus tempo. Existem três pernas do gráfico. Todas as três pernas são planas e retas. A primeira etapa mostra uma aceleração constante de 0. A segunda etapa mostra uma aceleração negativa constante. A terceira perna mostra uma aceleração negativa constante que não é tão negativa quanto a segunda perna.
    Figura\(\displaystyle \PageIndex{8}\)

    Resumo

    • Gráficos de movimento podem ser usados para analisar o movimento.
    • As soluções gráficas produzem soluções idênticas aos métodos matemáticos para derivar equações de movimento.
    • A inclinação de um gráfico de deslocamento\(\displaystyle x\) versus tempo\(\displaystyle t\) é a velocidade\(\displaystyle v\).
    • A inclinação de um gráfico de velocidade\(\displaystyle v\) versus\(\displaystyle t\) gráfico de tempo é aceleração\(\displaystyle a\).
    • A velocidade média, a velocidade instantânea e a aceleração podem ser obtidas analisando gráficos.

    Glossário

    variável independente
    a variável à qual a variável dependente é medida em relação a; geralmente plotada ao longo do\(x\) eixo -
    variável dependente
    a variável que está sendo medida; geralmente plotada ao longo do\(y\) eixo -
    inclinação
    a diferença no\(y\) valor -( o aumento) dividida pela diferença no\(x\) valor -( a corrida) de dois pontos em uma linha reta
    intercepção y
    o\(y\) valor -quando\(x\) =0 ou quando o gráfico cruza o\(y\) eixo -