2.7: Objetos caindo

objetivos de aprendizagem

Ao final desta seção, você poderá:

• Descreva os efeitos da gravidade em objetos em movimento.
• Descreva o movimento de objetos que estão em queda livre.
• Calcule a posição e a velocidade dos objetos em queda livre.

Objetos caindo

Objetos que caem formam uma classe interessante de problemas de movimento. Por exemplo, podemos estimar a profundidade de um poço vertical de mina jogando uma pedra nele e ouvindo a rocha atingir o fundo. Ao aplicar a cinemática desenvolvida até agora à queda de objetos, podemos examinar algumas situações interessantes e aprender muito sobre a gravidade no processo.

Gravidade

O fato mais notável e inesperado sobre a queda de objetos é que, se a resistência e o atrito do ar são insignificantes, em um determinado local todos os objetos caem em direção ao centro da Terra com a mesma aceleração constante, independente de sua massa. Esse fato determinado experimentalmente é inesperado, porque estamos tão acostumados com os efeitos da resistência e do atrito do ar que esperamos que objetos leves caiam mais lentamente do que objetos pesados.

Figura\(\PageIndex{1}\): Um martelo e uma pena cairão com a mesma aceleração constante se a resistência do ar for considerada insignificante. Essa é uma característica geral da gravidade não exclusiva da Terra, como demonstrou o astronauta David R. Scott na Lua em 1971, onde a aceleração devido à gravidade é apenas. 67 m/s 2.

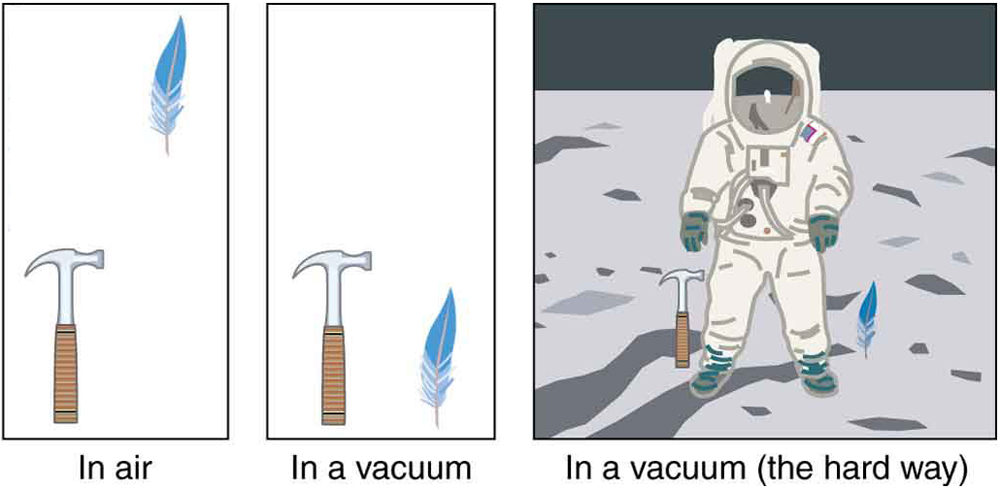
No mundo real, a resistência do ar pode fazer com que um objeto mais leve caia mais lentamente do que um objeto mais pesado do mesmo tamanho. Uma bola de tênis chegará ao chão depois que uma bola de beisebol forte cair ao mesmo tempo. (Pode ser difícil observar a diferença se a altura não for grande.) A resistência do ar se opõe ao movimento de um objeto no ar, enquanto o atrito entre objetos — como entre roupas e uma calha de lavanderia ou entre uma pedra e uma piscina na qual ela é jogada — também se opõe ao movimento entre eles. Para as situações ideais desses primeiros capítulos, um objeto caindo sem resistência ao ar ou atrito é definido como em queda livre.

A força da gravidade faz com que objetos caiam em direção ao centro da Terra. A aceleração de objetos em queda livre é, portanto, chamada de aceleração devido à gravidade. A aceleração devido à gravidade é constante, o que significa que podemos aplicar as equações cinemáticas a qualquer objeto em queda onde a resistência do ar e o atrito sejam insignificantes. Isso abre uma ampla classe de situações interessantes para nós. A aceleração devido à gravidade é tão importante que sua magnitude recebe seu próprio símbolo,. É constante em qualquer local da Terra e tem o valor médio

\[g=9.80 m/s^2.\]

Embora varie de. 78 m/s 2 a 9,83 m/s2, dependendo da latitude, altitude, formações geológicas subjacentes e topografia local, o valor médio de 9,80 m/s2 será usado neste texto, a menos que especificado de outra forma. A direção da aceleração devido à gravidade é descendente (em direção ao centro da Terra). Na verdade, sua direção define o que chamamos de vertical. Observe que se a aceleração a nas equações cinemáticas tem o valor +g ou −g depende de como definimos nosso sistema de coordenadas. Se definirmos a direção ascendente como negativa, então a=−g=−9,80 m/s2, e se definirmos a direção descendente como positiva, então = g = 9. 80 m/s 2.

Movimento unidimensional envolvendo gravidade

A melhor maneira de ver as características básicas do movimento que envolvem a gravidade é começar com as situações mais simples e depois avançar para situações mais complexas. Então, começamos considerando o movimento direto para cima e para baixo, sem resistência ao ar ou atrito. Essas suposições significam que a velocidade (se houver alguma) é vertical. Se o objeto cair, sabemos que a velocidade inicial é zero. Uma vez que o objeto tenha deixado contato com o que o tenha segurado ou jogado, o objeto está em queda livre. Nessas circunstâncias, o movimento é unidimensional e tem aceleração constante de magnitude g. Também representaremos o deslocamento vertical com o símbolo y e usaremos x para o deslocamento horizontal.

EQUAÇÕES CINEMÁTICAS PARA OBJETOS EM QUEDA LIVRE ONDE ACELERAÇÃO = -G

\(v=v_0−gt\)

\(y=y_0+v_0t−\frac{1}{2}gt^2\)

\(v^2=v^2_0−2g(y−y_0)\)

Exemplo\(\PageIndex{1}\): Calculating Position and Velocity of a Falling Object: A Rock Thrown Upward

Uma pessoa parada na beira de um penhasco alto joga uma pedra diretamente para cima com uma velocidade inicial de 13,0 m/s. A rocha perde a borda do penhasco ao cair de volta à terra. Calcule a posição e a velocidade da rocha 1,00 s, 2,00 s e 3,00 s após o lançamento, negligenciando os efeitos da resistência do ar.

Estratégia

Desenhe um esboço.

Figura\(\PageIndex{2}\)

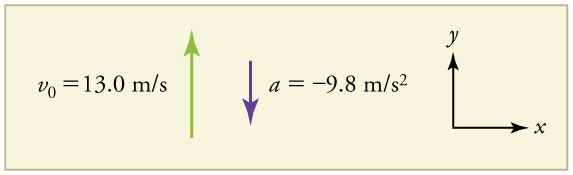
Somos solicitados a determinar a posição\(y\) em vários momentos. É razoável considerar\(y_0\) a posição inicial zero. Esse problema envolve movimento unidimensional na direção vertical. Usamos sinais de mais e menos para indicar a direção, com o aumento sendo positivo e o negativo para baixo. Como o aumento é positivo e a rocha é lançada para cima, a velocidade inicial também deve ser positiva. A aceleração devido à gravidade é descendente, então a é negativa. É crucial que a velocidade inicial e a aceleração devido à gravidade tenham sinais opostos. Sinais opostos indicam que a aceleração devido à gravidade se opõe ao movimento inicial e o diminuirá e, eventualmente, o reverterá.

Como são solicitados valores de posição e velocidade em três vezes, nos referiremos a eles como\(y_1\) e\(v_1; y_2\) e\(v_2\);\(y_3\) e\(v_3\) e.

Solução para posição\(y_1\)

1. Identifique os conhecidos. Nós sabemos disso\(y_0=0; v_0=13.0 m/s; a=−g=−9.80 m/s^2\); e\(t=1.00 s.\)

2. Identifique a melhor equação a ser usada. Usaremos\(y=y_0+v_0t+\frac{1}{2}at^2\) porque inclui apenas um desconhecido\(y\) (ou\(y_1\), aqui), que é o valor que queremos encontrar.

3. Insira os valores conhecidos e resolva\(y_1\).

\(y_1=0+(13.0 m/s)(1.00 s)+\frac{1}{2}(−9.80m/s^2)(1.00 s)^2=8.10m\)

Discussão

A rocha está 8,10 m acima de seu ponto de partida em\(t=1.00 s\), desde\(y_1>y_0\). Pode estar se movendo para cima ou para baixo; a única maneira de saber é calcular\(v_1\) e descobrir se é positivo ou negativo.

Solução para Velocity\(v_1\)

1. Identifique os conhecidos. Nós sabemos disso\(y_0=0; v_0=13.0 m/s; a=−g=−9.80 m/s^2\);\(t=1.00 s\) e. Também sabemos pela solução acima que\(y_1=8.10 m.\)

2. Identifique a melhor equação a ser usada. A mais direta é\(v=v_0−gt\) (de\(v=v_0+at\), onde a=aceleração gravitacional=−g).

3. Conecte os conhecidos e resolva.

\(v_1=v_0−gt=13.0 m/s−(9.80 m/s^2)(1.00 s)=3.20 m/s\)

Discussão

O valor positivo de\(v_1\) significa que a rocha ainda está subindo em\(t=1.00s\). No entanto, ele diminuiu em relação aos 13,0 m/s originais, conforme esperado.

Solução para os tempos restantes

Os procedimentos para calcular a posição e a velocidade em\(t=2.00s\) e\(3.00 s\) são os mesmos acima. Os resultados estão resumidos na Tabela e ilustrados na Figura.

Resultados

Hora, t	Posição, y	Velocidade, v	Aceleração, uma
. 100 s	. 10 m	. 20 m/s\)	9. 80 m/s^ 2\)
. 100 s	. 40 mm	6. 60 m/s\)	9. 80 m/s^ 2\)
. 100 s	5. 10 m	16. 4 m/s\)	9. 80 m/s^ 2\)

Representar graficamente os dados nos ajuda a entendê-los com mais clareza.

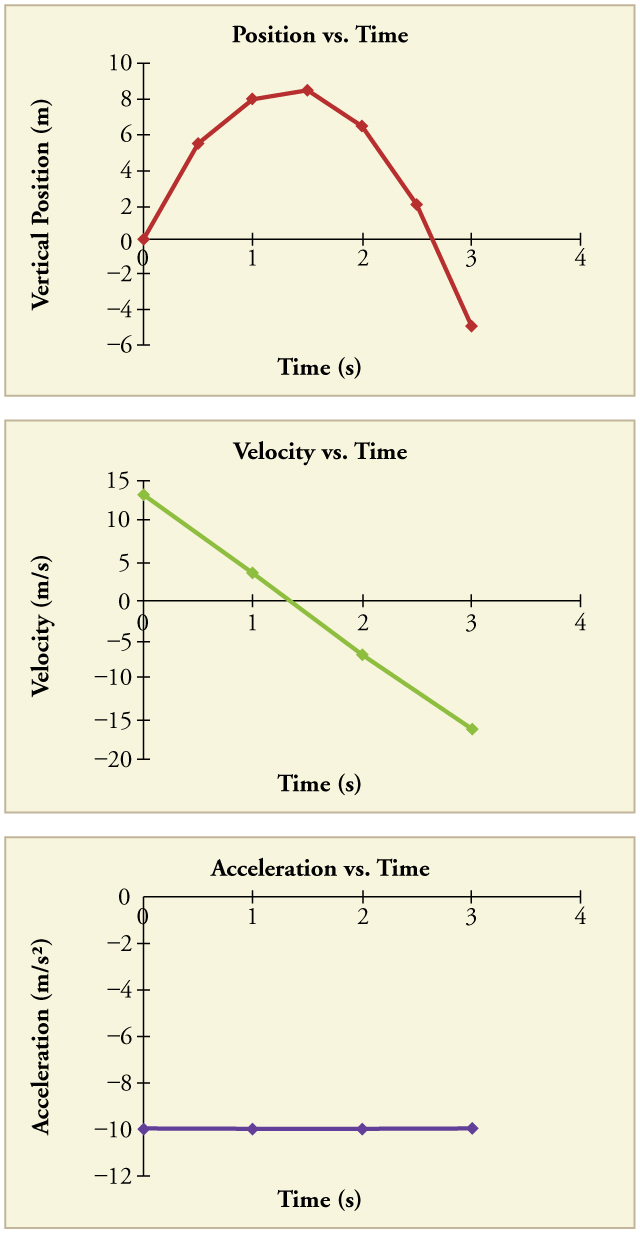
\(PageIndex{3}\): Posição vertical, velocidade vertical e aceleração vertical versus tempo de uma rocha lançada verticalmente na beira de um penhasco. Observe que a velocidade muda linearmente com o tempo e que a aceleração é constante. Alerta de conceito errado! Observe que o gráfico de posição versus tempo mostra somente a posição vertical. É fácil ter a impressão de que o gráfico mostra algum movimento horizontal — a forma do gráfico parece o caminho de um projétil. Mas esse não é o caso; o eixo horizontal é o tempo, não o espaço. O caminho real da rocha no espaço é reto para cima e para baixo.

Discussão

A interpretação desses resultados é importante. A 1,00 s, a rocha está acima de seu ponto de partida e se dirige para cima, já que\(y_1\) and \(v_1\) are both positive. At 2.00 s, the rock is still above its starting point, but the negative velocity means it is moving downward. At 3.00 s, both \(y_3\) and \(v_3\) are negative, meaning the rock is below its starting point and continuing to move downward. Notice that when the rock is at its highest point (at 1.5 s), its velocity is zero, but its acceleration is still \(−9.80 m/s^2\). Its acceleration is \(−9.80 m/s^2\) for the whole trip—while it is moving up and while it is moving down. Note that the values for y are the positions (or displacements) of the rock, not the total distances traveled. Finally, note that free-fall applies to upward motion as well as downward. Both have the same acceleration—the acceleration due to gravity, which remains constant the entire time. Astronauts training in the famous Vomit Comet, for example, experience free-fall while arcing up as well as down, as we will discuss in more detail later.The interpretation of these results is important. At 1.00 s the rock is above its starting point and heading upward, since y1 and v1 are both positive. At 2.00 s, the rock is still above its starting point, but the negative velocity means it is moving downward. At 3.00 s, both y3 and v3 are negative, meaning the rock is below its starting point and continuing to move downward. Notice that when the rock is at its highest point (at 1.5 s), its velocity is zero, but its acceleration is still −9.80 m/s2. Its acceleration is −9.80 m/s2 for the whole trip—while it is moving up and while it is moving down. Note that the values for y are the positions (or displacements) of the rock, not the total distances traveled. Finally, note that free-fall applies to upward motion as well as downward. Both have the same acceleration—the acceleration due to gravity, which remains constant the entire time. Astronauts training in the famous Vomit Comet, for example, experience free-fall while arcing up as well as down, as we will discuss in more detail later.

MAKING CONNECTIONS: TAKE-HOME EXPERIMENT—REACTION TIME

A simple experiment can be done to determine your reaction time. Have a friend hold a ruler between your thumb and index finger, separated by about 1 cm. Note the mark on the ruler that is right between your fingers. Have your friend drop the ruler unexpectedly, and try to catch it between your two fingers. Note the new reading on the ruler. Assuming acceleration is that due to gravity, calculate your reaction time. How far would you travel in a car (moving at 30 m/s) if the time it took your foot to go from the gas pedal to the brake was twice this reaction time?

Example \(\PageIndex{2}\):Calculating Velocity of a Falling Object: A Rock Thrown Down

What happens if the person on the cliff throws the rock straight down, instead of straight up? To explore this question, calculate the velocity of the rock when it is 5.10 m below the starting point, and has been thrown downward with an initial speed of 13.0 m/s.

Strategy

Draw a sketch.

Figure \(\PageIndex{4}\)

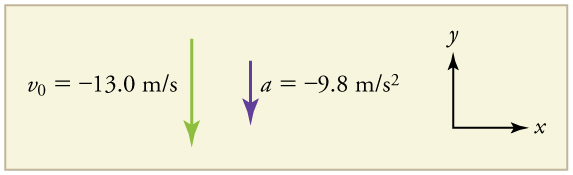
Since up is positive, the final position of the rock will be negative because it finishes below the starting point at \(y_0=0\). Similarly, the initial velocity is downward and therefore negative, as is the acceleration due to gravity. We expect the final velocity to be negative since the rock will continue to move downward.

Solution

1. Identify the knowns. \(y_0=0; y_1=−5.10 m; v_0=−13.0 m/s; a=−g=−9.80 m/s^2\).

2. Choose the kinematic equation that makes it easiest to solve the problem. The equation \(v^2=v^2_0+2a(y−y_0)\) works well because the only unknown in it is \(v\). (We will plug \(y_1\) in for \(y\).)

3. Enter the known values

\(v^2=(−13.0 m/s)^2+2(−9.80 m/s^2)(−5.10 m−0 m)=268.96 m^2/s^2,\)

where we have retained extra significant figures because this is an intermediate result.

Taking the square root, and noting that a square root can be positive or negative, gives

\(v=±16.4 m/s.\)

The negative root is chosen to indicate that the rock is still heading down. Thus,

\(v=−16.4 m/s.\)

Discussion

Note that this is exactly the same velocity the rock had at this position when it was thrown straight upward with the same initial speed. (See Example and Figure(a).) This is not a coincidental result. Because we only consider the acceleration due to gravity in this problem, the speed of a falling object depends only on its initial speed and its vertical position relative to the starting point. For example, if the velocity of the rock is calculated at a height of 8.10 m above the starting point (using the method from Example) when the initial velocity is 13.0 m/s straight up, a result of \(±3.20 m/s\) is obtained. Here both signs are meaningful; the positive value occurs when the rock is at 8.10 m and heading up, and the negative value occurs when the rock is at 8.10 m and heading back down. It has the same speed but the opposite direction.

Figure \(PageIndex{5}\): (a) A person throws a rock straight up, as explored in Example. The arrows are velocity vectors at 0, 1.00, 2.00, and 3.00 s. (b) A person throws a rock straight down from a cliff with the same initial speed as before, as in Example. Note that at the same distance below the point of release, the rock has the same velocity in both cases.

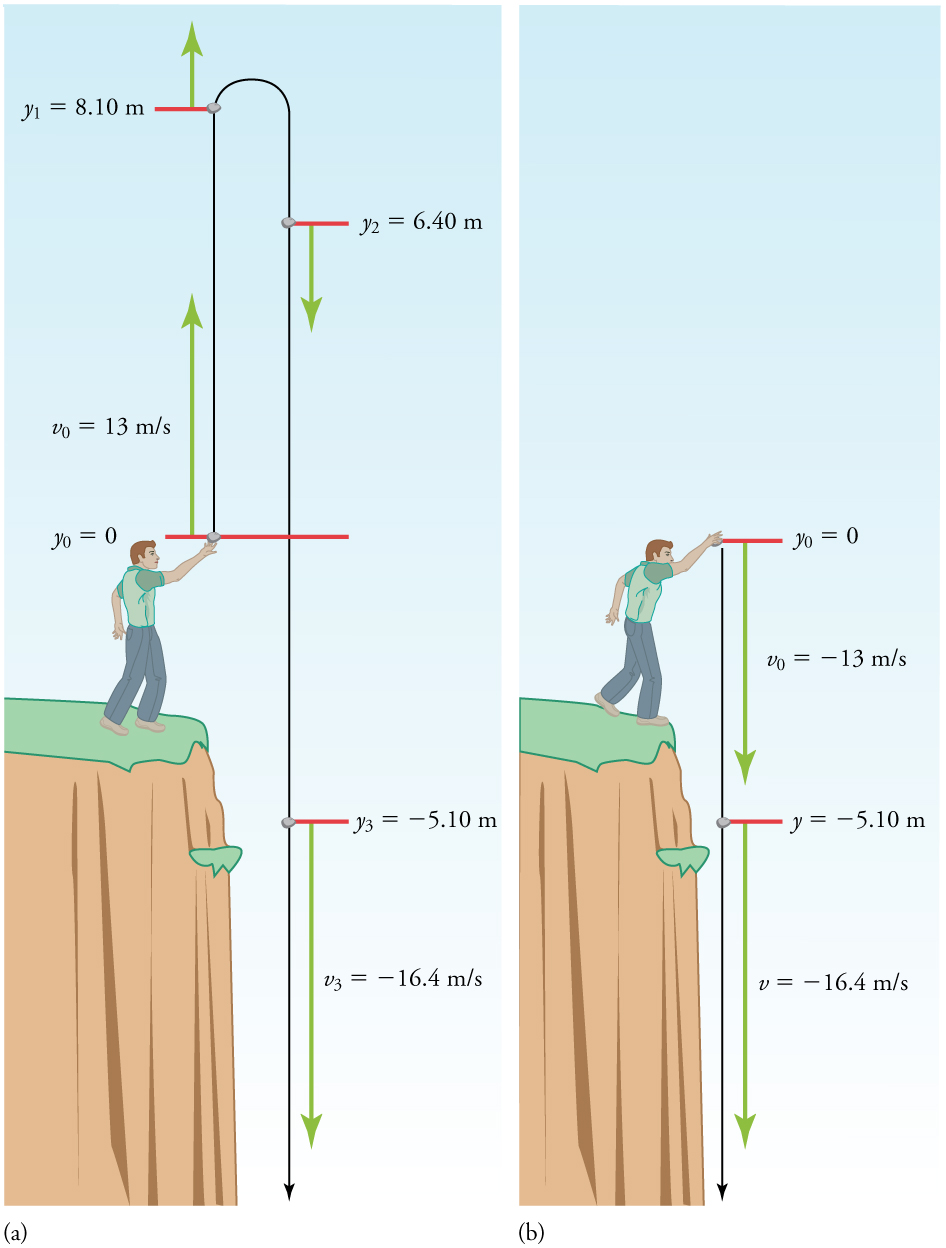
Another way to look at it is this: In Example, the rock is thrown up with an initial velocity of \(13.0 m/s\). It rises and then falls back down. When its position is \(y=0\) on its way back down, its velocity is \(−13.0 m/s\). That is, it has the same speed on its way down as on its way up. We would then expect its velocity at a position of \(y=−5.10\) m to be the same whether we have thrown it upwards at \(+13.0 m/s\) or thrown it downwards at \(−13.0 m/s\). The velocity of the rock on its way down from \(y=0\) is the same whether we have thrown it up or down to start with, as long as the speed with which it was initially thrown is the same.

Example \(\PageIndex{3}\):Find g from Data on a Falling Object

The acceleration due to gravity on Earth differs slightly from place to place, depending on topography (e.g., whether you are on a hill or in a valley) and subsurface geology (whether there is dense rock like iron ore as opposed to light rock like salt beneath you.) The precise acceleration due to gravity can be calculated from data taken in an introductory physics laboratory course. An object, usually a metal ball for which air resistance is negligible, is dropped and the time it takes to fall a known distance is measured. See, for example, Figure. Very precise results can be produced with this method if sufficient care is taken in measuring the distance fallen and the elapsed time.

Figure \(\PageIndex{6}\): Positions and velocities of a metal ball released from rest when air resistance is negligible. Velocity is seen to increase linearly with time while displacement increases with time squared. Acceleration is a constant and is equal to gravitational acceleration.

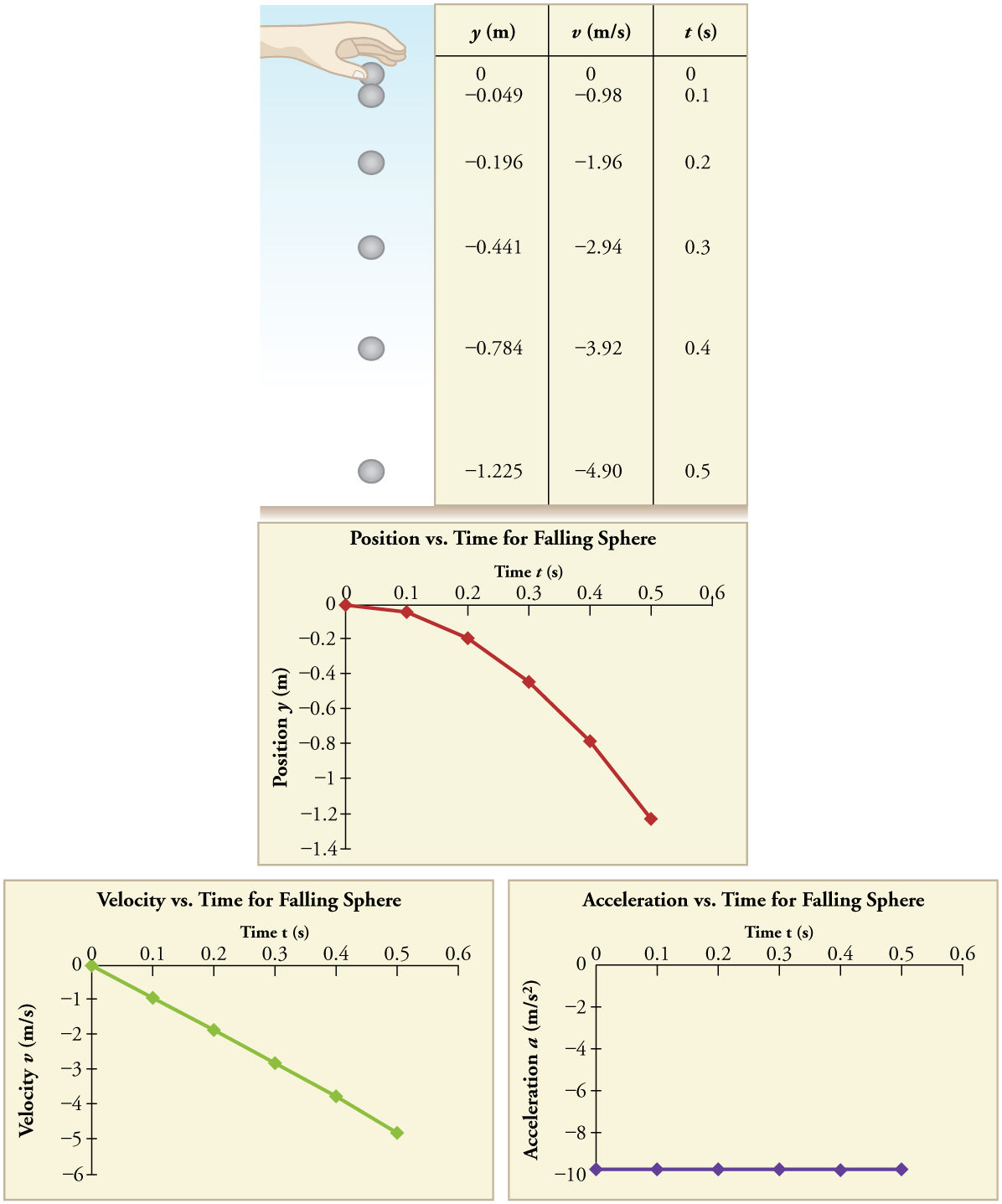
Suppose the ball falls 1.0000 m in 0.45173 s. Assuming the ball is not affected by air resistance, what is the precise acceleration due to gravity at this location?

Strategy

Draw a sketch.

Figure \(\PageIndex{7}\):

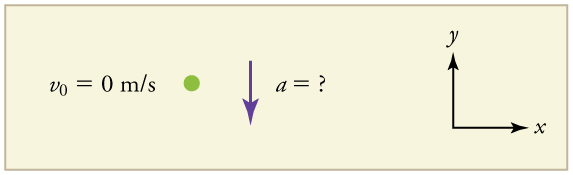
We need to solve for acceleration \(a.\) Note that in this case, displacement is downward and therefore negative, as is acceleration.

Solution

1. Identify the knowns. \(y_0=0; y=–1.0000 m; t=0.45173; v_0=0.\)

2. Choose the equation that allows you to solve for \(a\) using the known values.

\(y=y_0+v_0t+\frac{1}{2}at^2\)

3. Substitute 0 for \(v_0\) and rearrange the equation to solve for \(a\). Substituting 0 for \(v_0\)yields

\(y=y_0+\frac{1}{2}at^2\).

Solving for \(a\) gives

\(a=\frac{2(y−y_0)}{t^2}\).

4. Substitute known values yields

\(a=\frac{2(−1.0000 m – 0)}{(0.45173 s)^2}=−9.8010 m/s^2,\)

so, because \(a=−g\) with the directions we have chosen,

\(g=9.8010 m/s^2.\)

Discussion

The negative value for a indicates that the gravitational acceleration is downward, as expected. We expect the value to be somewhere around the average value of \(9.80 m/s^2\), so \(9.8010 m/s^2\) makes sense. Since the data going into the calculation are relatively precise, this value for g is more precise than the average value of \(9.80 m/s%2\); it represents the local value for the acceleration due to gravity.

Exercise \(\PageIndex{1}\)

A chunk of ice breaks off a glacier and falls 30.0 meters before it hits the water. Assuming it falls freely (there is no air resistance), how long does it take to hit the water?

Answer

We know that initial position \(y_0=0\), final position \(y=−30.0 m\), and \(a=−g=−9.80 m/s^2\). We can then use the equation \(y=y_0+v_0t+\frac{1}{2}at^2\) to solve for \(t\). Inserting \(a=−g\), we obtain

\(y=0+0−\frac{1}{2}gt^2\)

\(t^2=\frac{2y}{−g}\)

\(t=±\sqrt{\frac{2y}{−g}}=±\sqrt{\frac{2(−30.0 m)}{−9.80 m/s^2}}=±\sqrt{6.12s^2}=2.47 s≈2.5 s\)

where we take the positive value as the physically relevant answer. Thus, it takes about 2.5 seconds for the piece of ice to hit the water.

PHET EXPLORATIONS: EQUATION GRAPHER

Learn about graphing polynomials. The shape of the curve changes as the constants are adjusted. View the curves for the individual terms (e.g. \(y=bx\)) to see how they add to generate the polynomial curve.

Figure \(\PageIndex{8}\): Equation Grapher

Summary

• An object in free-fall experiences constant acceleration if air resistance is negligible.
• On Earth, all free-falling objects have an acceleration due to gravity \(g\), which averages

\(g=9.80 m/s^2\).

• Whether the acceleration a should be taken as \(+g\) or \(−g\) is determined by your choice of coordinate system. If you choose the upward direction as positive, \(a=−g=−9.80 m/s^2\) is negative. In the opposite case, \(a=+g=9.80 m/s^2\) is positive. Since acceleration is constant, the kinematic equations above can be applied with the appropriate \(+g\) or \(−g\) substituted for a.
• For objects in free-fall, up is normally taken as positive for displacement, velocity, and acceleration.

Glossary

free-fall

the state of movement that results from gravitational force only

acceleration due to gravity

acceleration of an object as a result of gravity